являются точка, прямая и плоскость.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Стереометрия презентация
Содержание
- 1. Стереометрия
- 2. Часть I Плоскость. Аксиомы стереометрии ( первая,
- 3. Плоскость. На рисунках плоскости изображаются в виде
- 4. Аксиомы стереометрии.
- 5. Через любые три точки, не лежащие на
- 6. Аксиома №3 Если две различные плоскости имеют
- 7. Некоторые следствия из аксиом Аксиома №1 (Следствие)
- 8. Часть II (параллельные прямые)
- 9. Параллельность прямых и плоскостей Две прямые в
- 10. Через любую точку пространства, не лежащую на
- 11. Теорема о трех прямых в пространстве. Если
- 12. Параллельность прямой и плоскости Прямая и плоскость
- 13. Теорема №2 Если плоскость проходит через данную
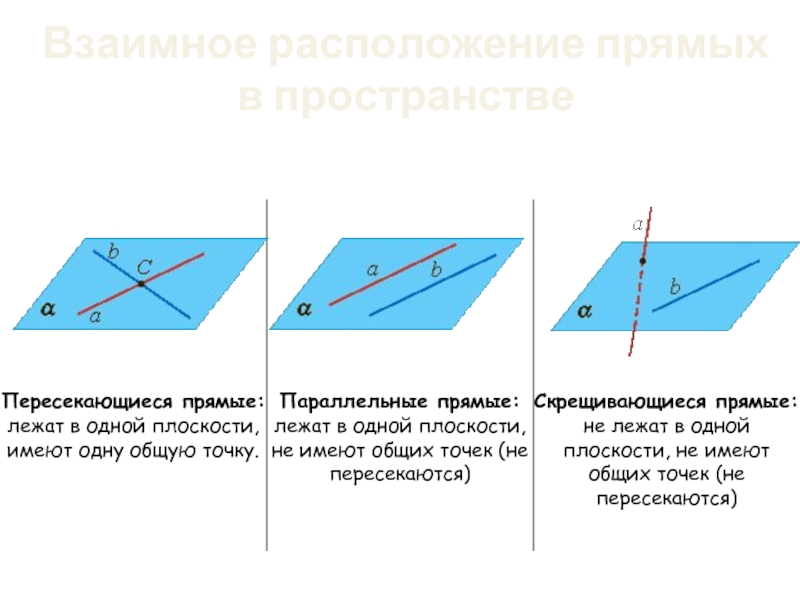
- 14. Взаимное расположение прямых в пространстве
- 15. Часть II (параллельные прямые) Параллельность плоскостей
- 16. Две плоскости называются параллельными, если
- 17. Признак параллельности двух плоскостей Теорема.
- 18. Свойства параллельных плоскостей Вели α∥β и
- 19. Часть III (Декартовы координаты и векторы в пространстве)
- 20. Прямоугольная, или Декартова система координат — наиболее простая
- 21. Возьмем три взаимно перпендикулярные прямые x, y, z,
- 22. Параллельный перенос Введём на плоскости декартовы координаты xОу.
- 23. Понятие вектора Величины, которые характеризуются, не только числом, но
- 24. Вектор характеризуется следующими элементами: 1) начальной точкой
- 25. Два вектора называются равными, если они совмещаются
- 26. Свойство коллинеарных векторов Если векторы и коллинеарны
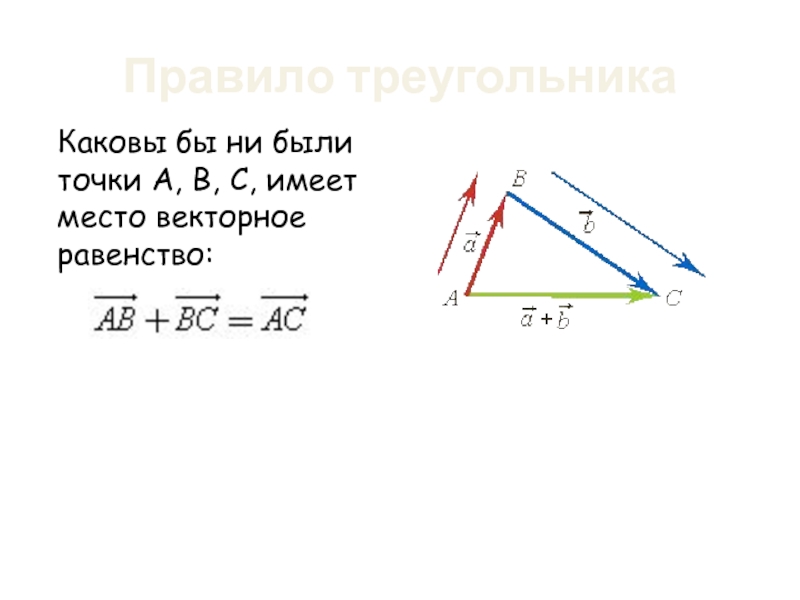
- 27. Правило треугольника Каковы бы ни были точки А, В, С, имеет место векторное равенство:
- 28. Рисунки иллюстрируют сложение коллинеарных векторов с помощью параллельного переноса.
- 29. Правило параллелограмма Если векторы и
- 30. Свойства сложения векторов Для любых векторов
- 31. Правило многоугольника Применяется, если нужно найти сумму
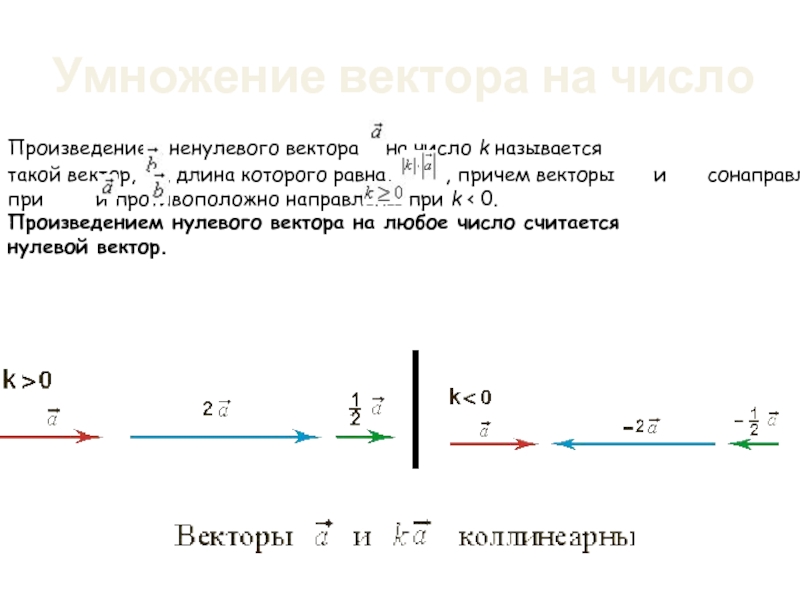
- 32. Умножение вектора на число Произведением ненулевого вектора
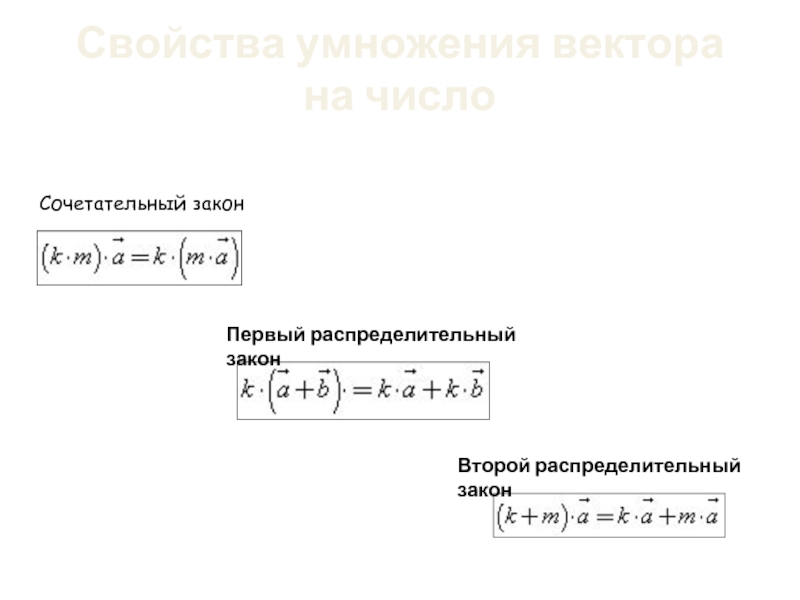
- 33. Свойства умножения вектора на число Сочетательный закон Первый распределительный закон Второй распределительный закон
- 34. Компланарные векторы Векторы называются компланарными, если при откладывании их
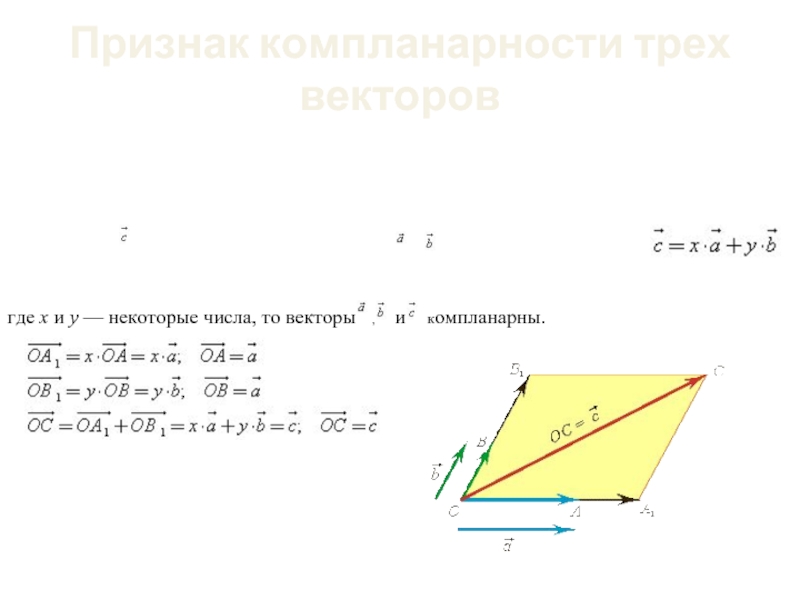
- 35. Признак компланарности трех векторов Если вектор можно
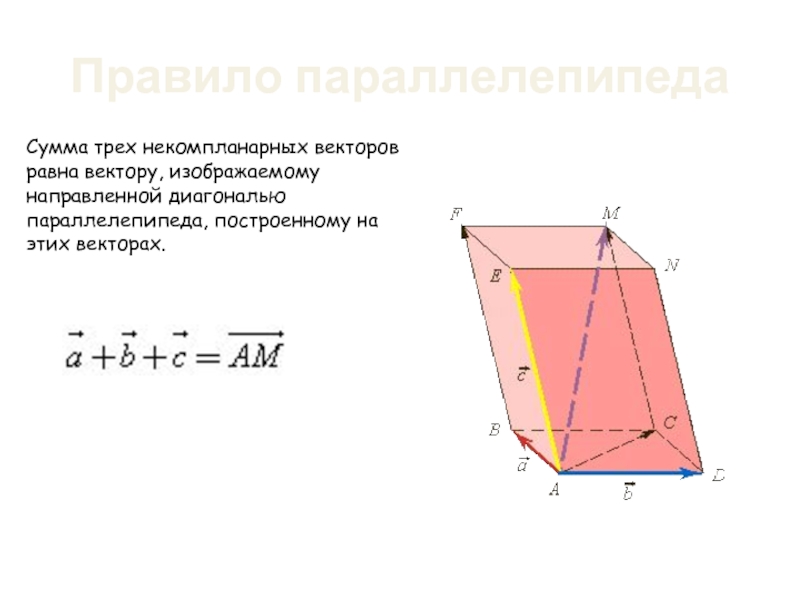
- 36. Правило параллелепипеда Сумма трех некомпланарных векторов равна
- 37. Базис вектора. Разложение вектора на плоскости по
- 38. Разложение вектора по трем некомпланарным векторам Базисом
- 39. Действия над векторами, заданными своими координатами
Часть I Плоскость. Аксиомы стереометрии ( первая, вторая, третья). Некоторые следствия из аксиом.
Слайд 1
Стереометрия
Раздел геометрии, в котором изучаются фигуры в пространстве. Основными фигурами в пространстве
Слайд 2Часть I
Плоскость.
Аксиомы стереометрии ( первая, вторая, третья).
Некоторые следствия из аксиом.
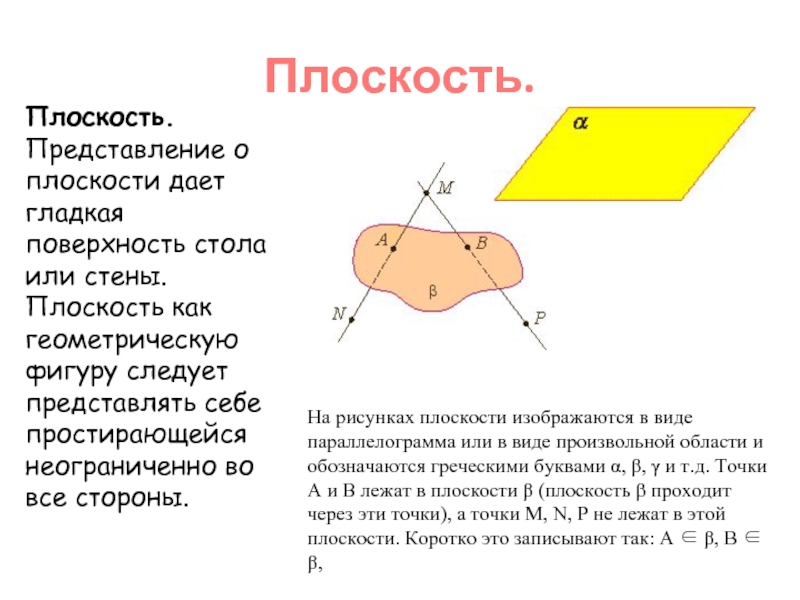
Слайд 3Плоскость.
На рисунках плоскости изображаются в виде параллелограмма или в виде произвольной
области и обозначаются греческими буквами α, β, γ и т.д. Точки А и В лежат в плоскости β (плоскость β проходит через эти точки), а точки M, N, P не лежат в этой плоскости. Коротко это записывают так: А ∈ β, B ∈ β,
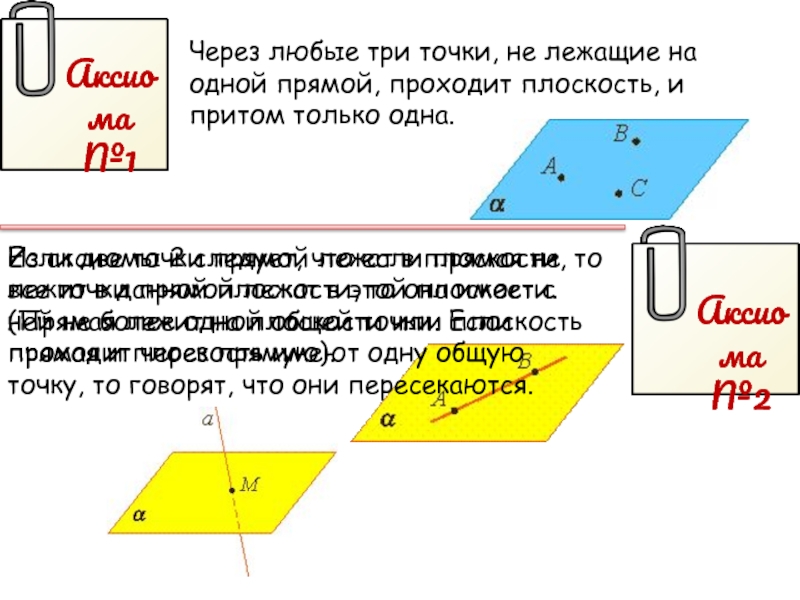
Слайд 5Через любые три точки, не лежащие на одной прямой, проходит плоскость,
и притом только одна.
Аксиома №1
Аксиома №2
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. (Прямая лежит на плоскости или плоскость проходит через прямую).
Из аксиомы 2 следует, что если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки. Если прямая и плоскость имеют одну общую точку, то говорят, что они пересекаются.
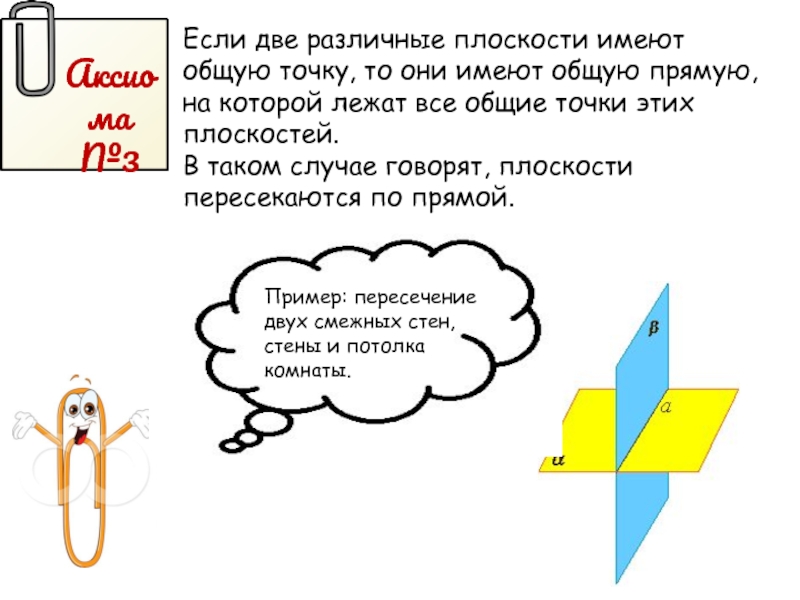
Слайд 6Аксиома №3
Если две различные плоскости имеют общую точку, то они имеют
общую прямую, на которой лежат все общие точки этих плоскостей.
В таком случае говорят, плоскости пересекаются по прямой.
В таком случае говорят, плоскости пересекаются по прямой.
Пример: пересечение двух смежных стен, стены и потолка комнаты.
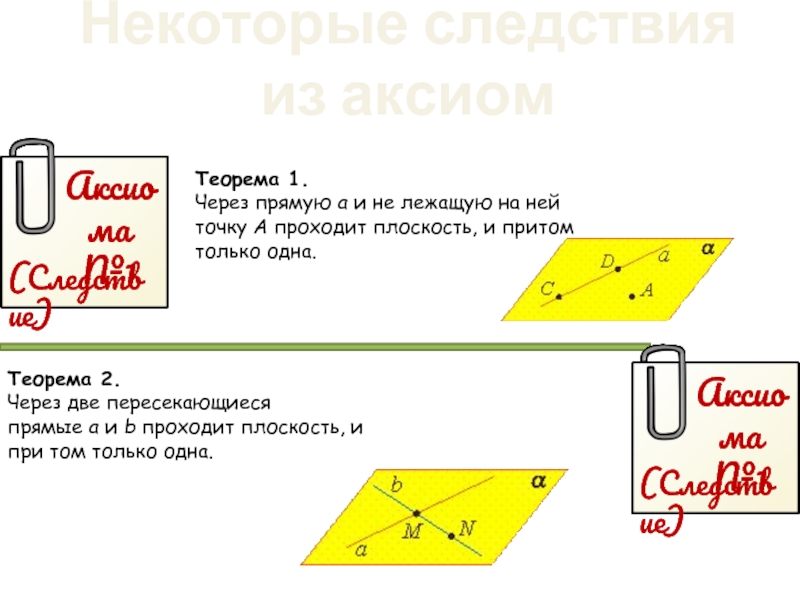
Слайд 7Некоторые следствия из аксиом
Аксиома №1
(Следствие)
Теорема 1.
Через прямую a и не лежащую на ней
точку А проходит плоскость, и притом только одна.
Аксиома №1
(Следствие)
Теорема 2.
Через две пересекающиеся прямые a и b проходит плоскость, и при том только одна.
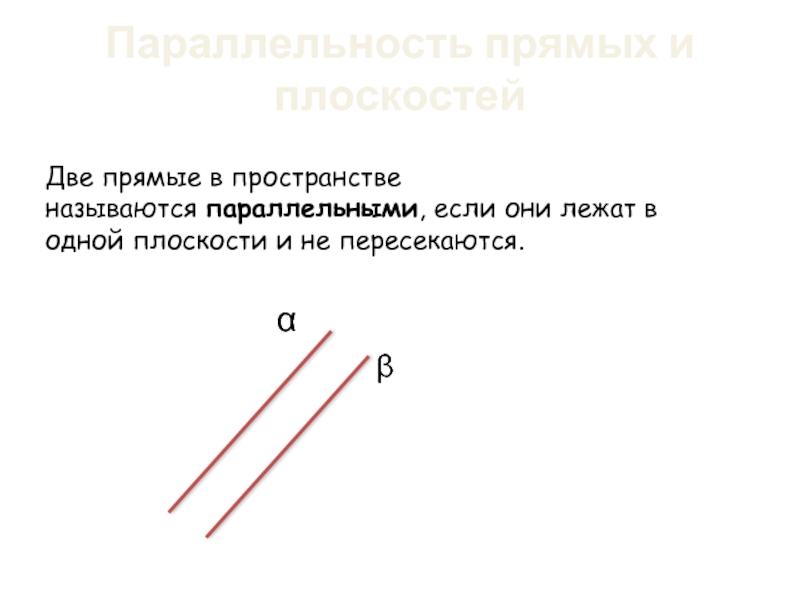
Слайд 9Параллельность прямых и плоскостей
Две прямые в пространстве называются параллельными, если они лежат
в одной плоскости и не пересекаются.
α
β
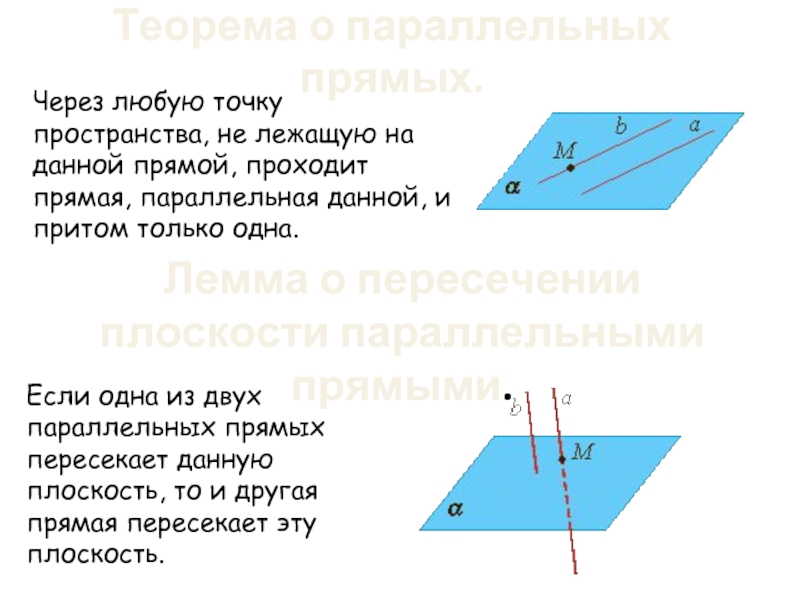
Слайд 10Через любую точку пространства, не лежащую на данной прямой, проходит прямая,
параллельная данной, и притом только одна.
Теорема о параллельных прямых.
Лемма о пересечении плоскости параллельными прямыми.
Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.
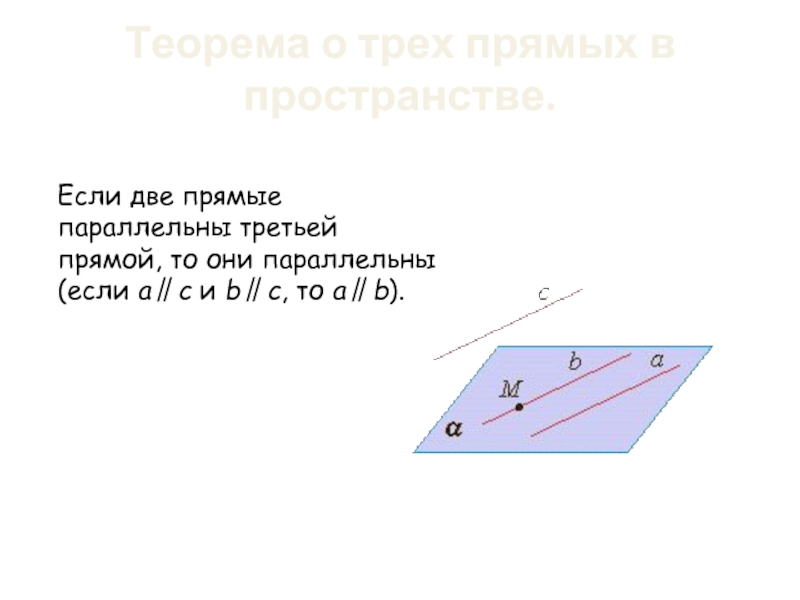
Слайд 11Теорема о трех прямых в пространстве.
Если две прямые параллельны третьей прямой,
то они параллельны (если a∥c и b∥c, то a∥b).
Слайд 12Параллельность прямой и плоскости
Прямая и плоскость называются параллельными, если они не
имеют общих точек.
Признак параллельности прямой и плоскости
Теорема №1
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
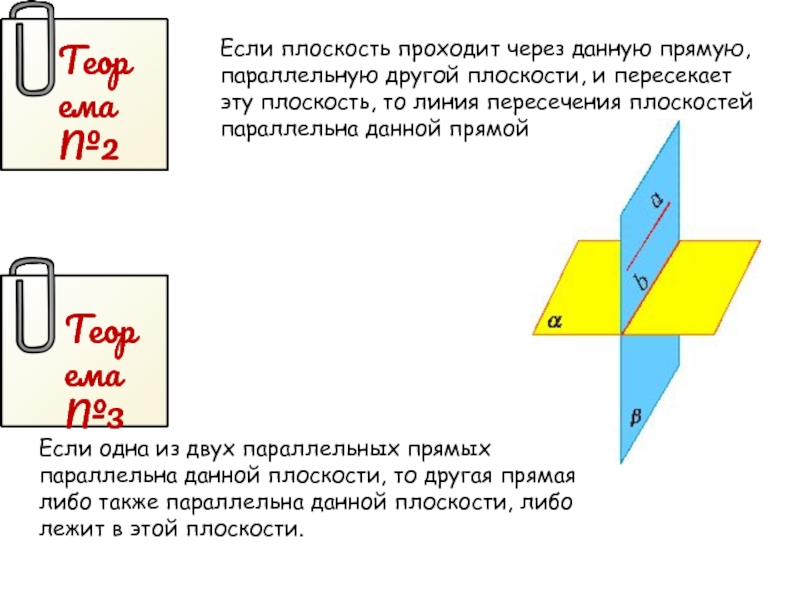
Слайд 13Теорема №2
Если плоскость проходит через данную прямую, параллельную другой плоскости, и
пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.
Теорема №3
Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.
Слайд 16
Две плоскости называются параллельными, если они не пересекаются, т.е. не имеют
ни одной общей точки. α∥β.
Слайд 17
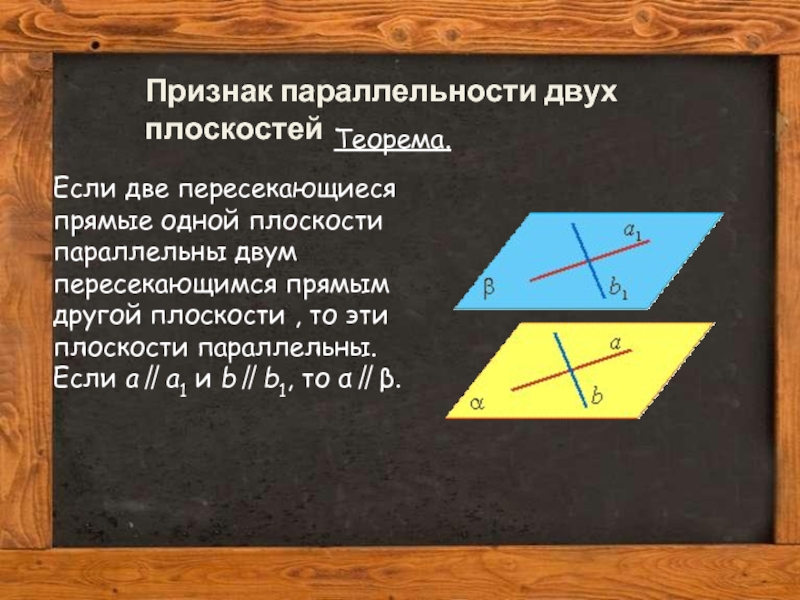
Признак параллельности двух плоскостей
Теорема.
Если две пересекающиеся прямые одной плоскости параллельны двум
пересекающимся прямым другой плоскости , то эти плоскости параллельны.
Если а∥а1 и b∥b1, то α∥β.
Слайд 18
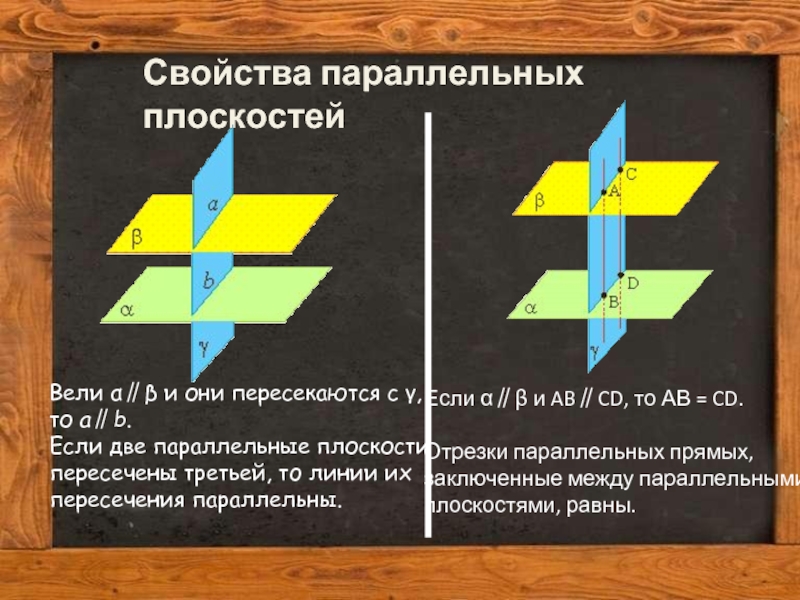
Свойства параллельных плоскостей
Вели α∥β и они пересекаются с γ, то а∥b.
Если две
параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Если α∥β и AB∥CD, то АВ = CD.
Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Слайд 20
Прямоугольная, или Декартова система координат — наиболее простая и поэтому часто используемая система координат на
плоскости и в пространстве.
Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Рассуждение о методе» в 1637 году. Поэтому прямоугольную систему координат называют также —Декартова система координат.
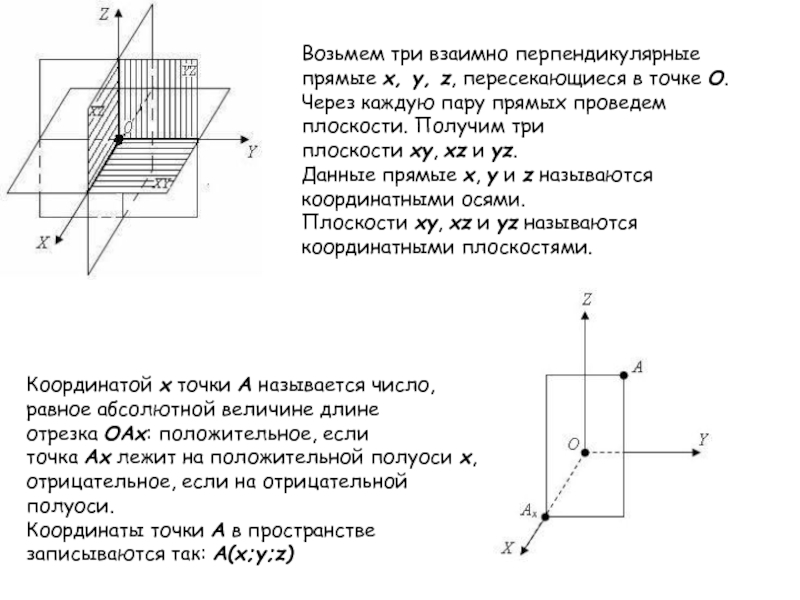
Слайд 21Возьмем три взаимно перпендикулярные прямые x, y, z, пересекающиеся в точке O. Через
каждую пару прямых проведем плоскости. Получим три плоскости xy, xz и yz.
Данные прямые x, y и z называются координатными осями.
Плоскости xy, xz и yz называются координатными плоскостями.
Данные прямые x, y и z называются координатными осями.
Плоскости xy, xz и yz называются координатными плоскостями.
Координатой x точки A называется число, равное абсолютной величине длине отрезка OAx: положительное, если точка Ax лежит на положительной полуоси x, отрицательное, если на отрицательной полуоси.
Координаты точки A в пространстве записываются так: A(x;y;z)
Слайд 22Параллельный перенос
Введём на плоскости декартовы координаты xОу. Преобразование некоторой фигуры F, при
котором произвольная ее точка А (х;у) переходит в другую точку А (х+a; y+b), где а и b постоянные, называется параллельным переносом;
Параллельный перенос есть движение. При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.
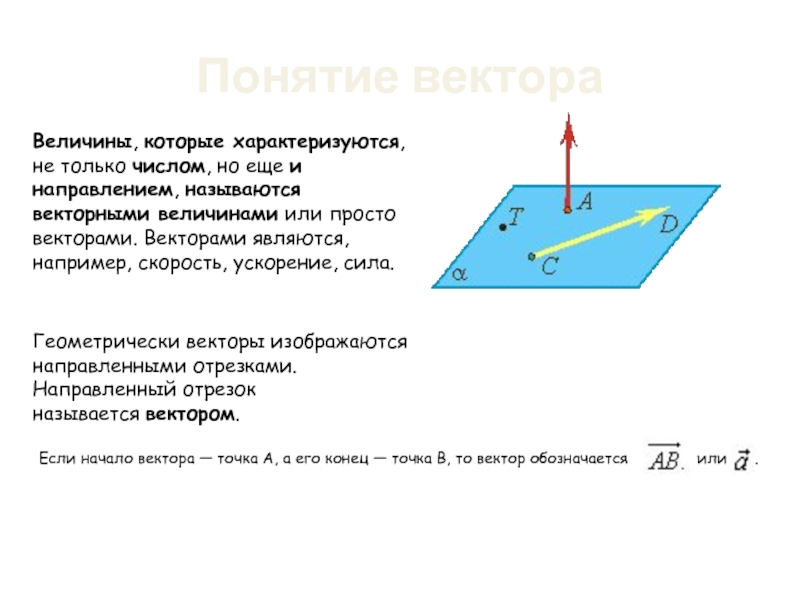
Слайд 23Понятие вектора
Величины, которые характеризуются, не только числом, но еще и направлением, называются векторными величинами или просто
векторами. Векторами являются, например, скорость, ускорение, сила.
Геометрически векторы изображаются направленными отрезками.
Направленный отрезок называется вектором.
Если начало вектора — точка А, а его конец — точка В, то вектор обозначается или .
Слайд 24Вектор характеризуется следующими элементами: 1) начальной точкой (точкой приложения); 2 )направлением; 3) длиной («модулем
вектора»).
От любой точки можно отложить вектор, равный данному, и притом только один, используя параллельный перенос.
Нулевой вектор — точка в пространстве. Начало и конец нулевого вектора совпадают, и он не имеет длины и направления.
Обозначается: .
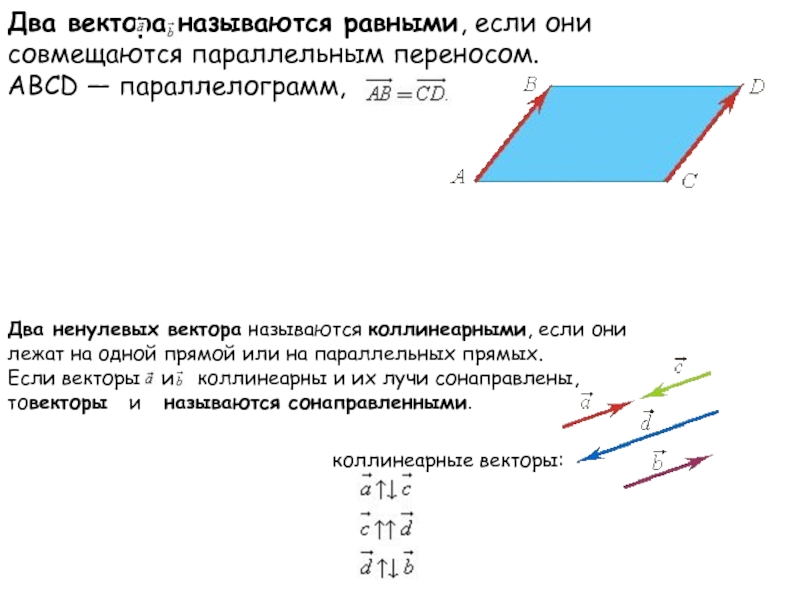
Слайд 25Два вектора называются равными, если они совмещаются параллельным переносом. АВСD — параллелограмм,
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Если векторы и коллинеарны и их лучи сонаправлены, товекторы и называются сонаправленными.
коллинеарные векторы:
Слайд 26Свойство коллинеарных векторов
Если векторы и коллинеарны и , то существует число k такое,
что . причем если k > 0, то векторы и сонаправленные, если k < 0, то противоположно направленные.
е
Слайд 28Рисунки иллюстрируют сложение коллинеарных векторов с помощью параллельного переноса.
Если при сложении векторов
и по правилу треугольника точку А заменить другой точкойА1, то вектор заменится равным ему вектором .
Слайд 29
Правило параллелограмма
Если векторы и неколлинеарны, их можно отложить от одной точки,
достроив затем параллелограмм.
Диагональ параллелограмма есть сумма двух векторов и .
Слайд 30
Свойства сложения векторов
Для любых векторов заданных в
пространстве, справедливы равенства:
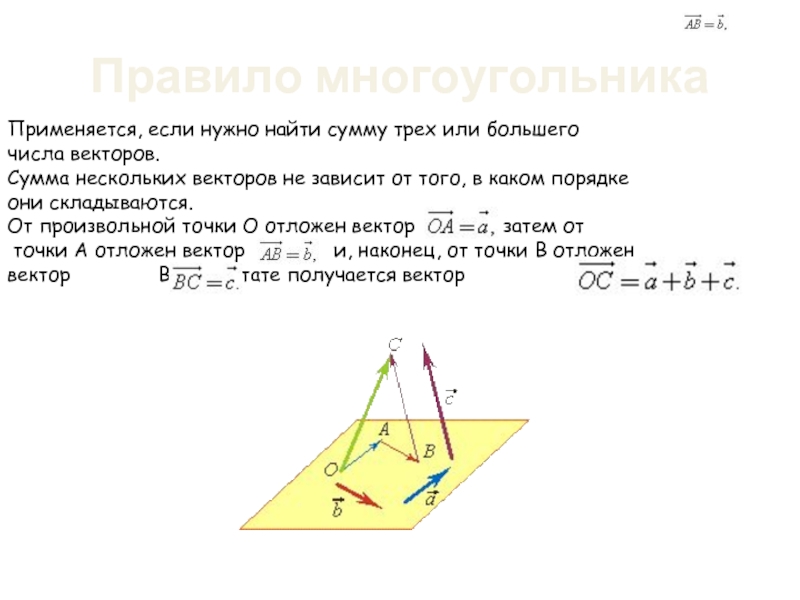
Слайд 31Правило многоугольника
Применяется, если нужно найти сумму трех или большего числа векторов.
Сумма
нескольких векторов не зависит от того, в каком порядке они складываются.
От произвольной точки О отложен вектор затем от
точки А отложен вектор и, наконец, от точки В отложен вектор В результате получается вектор
точки А отложен вектор и, наконец, от точки В отложен вектор В результате получается вектор
Слайд 32Умножение вектора на число
Произведением ненулевого вектора на число k называется такой вектор,
, длина которого равна, , причем векторы и сонаправлены при и противоположно направлены при k < 0.
Произведением нулевого вектора на любое число считается нулевой вектор.
Слайд 33Свойства умножения вектора на число
Сочетательный закон
Первый распределительный закон
Второй распределительный закон
Слайд 34Компланарные векторы
Векторы называются компланарными, если при откладывании их от одной и той же
точки они будут лежать в одной плоскости. Любые два вектора компланарны.
Три вектора, среди которых имеются два коллинеарных, также компланарны.
Три произвольных вектора могут быть компланарными (лежать в одной плоскости) или некомпланарными (не лежать в одной плоскости).
Три вектора, среди которых имеются два коллинеарных, также компланарны.
Три произвольных вектора могут быть компланарными (лежать в одной плоскости) или некомпланарными (не лежать в одной плоскости).
Слайд 35Признак компланарности трех векторов
Если вектор можно разложить по векторам и ,
т.е. представить в виде
где х и у — некоторые числа, то векторы , и компланарны.
Слайд 36Правило параллелепипеда
Сумма трех некомпланарных векторов равна вектору, изображаемому направленной диагональю параллелепипеда,
построенному на этих векторах.
Слайд 37Базис вектора. Разложение вектора на плоскости по двум некомпланарным векторам
Теорема: Любой вектор
на плоскости может быть представлен, и притом единственным образом, в виде двух любых неколлинеарных векторов и :
Числа x и y называются координатами вектора. Векторы и называются базисом вектора на плоскости.
Слайд 38Разложение вектора по трем некомпланарным векторам
Базисом пространства называют любые три некомпланарных
вектора, взятые в определенном порядке
Теорема: Любой вектор на плоскости может быть представлен, и притом единственным образом, в виде линейной комбинации трех любых неколлинеарных векторов , и : :
Числа x, y и z называются координатами вектора в данном базисе. В этом случае пишут:
