- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы уравнений. презентация
Содержание
- 1. Системы уравнений.
- 2. План урока. 1.Актуализация знаний. 2.Системы линейных уравнений. 3.Нелинейные системы. 4.Отработка умений и навыков. 5.Итог урока.
- 3. 1.Повтори! ! ! 1.Что называется системой уравнений?
- 4. Теория темы. Каждая пара значений переменных, которая
- 5. Теория темы. 1.Системой уравнений называется некоторое количество
- 6. Теория темы. 3.Решить систему уравнений –это значит
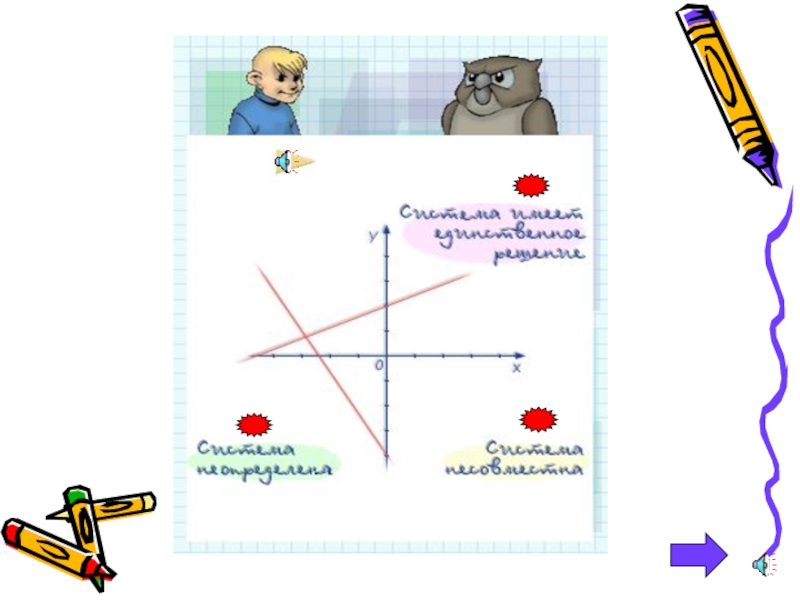
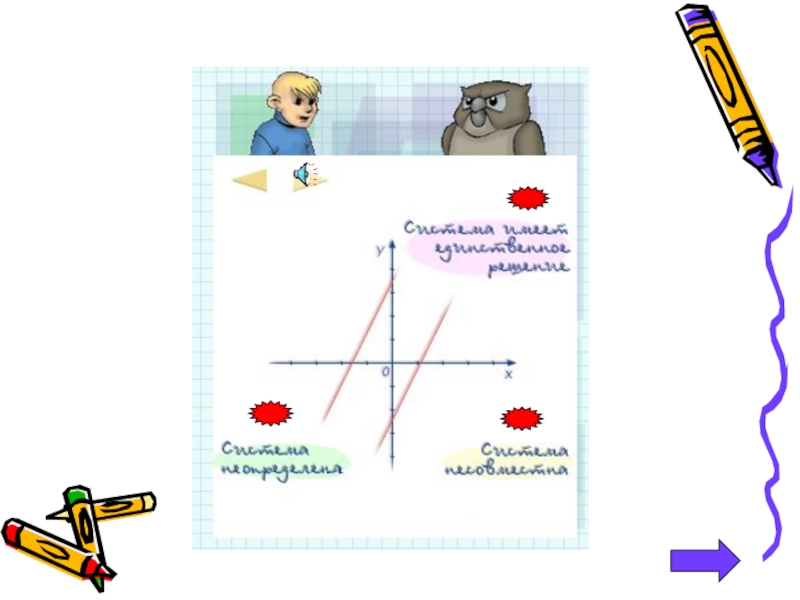
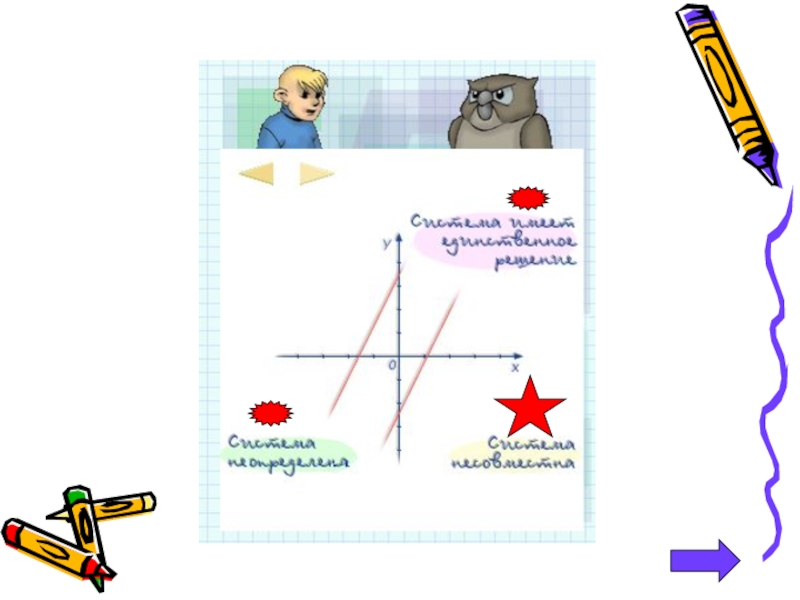
- 7. Графический метод решения систем линейных уравнений.
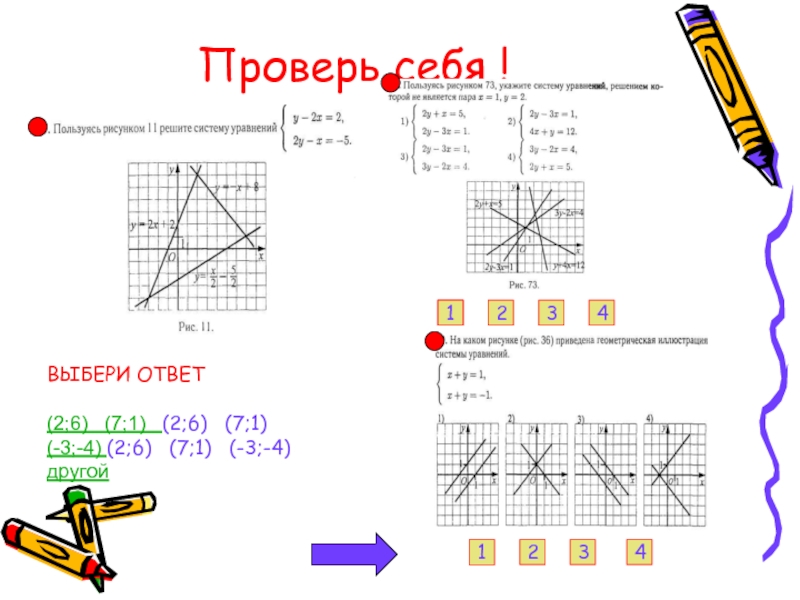
- 12. Проверь себя ! ВЫБЕРИ ОТВЕТ
- 13. подумай ещё
- 14. молодец!
- 15. Графический метод решения уравнения. Графический метод
- 16. Выбери ответ: (1;2), (-2;-1)
- 17. Правильно!
- 18. Неверно! вернись
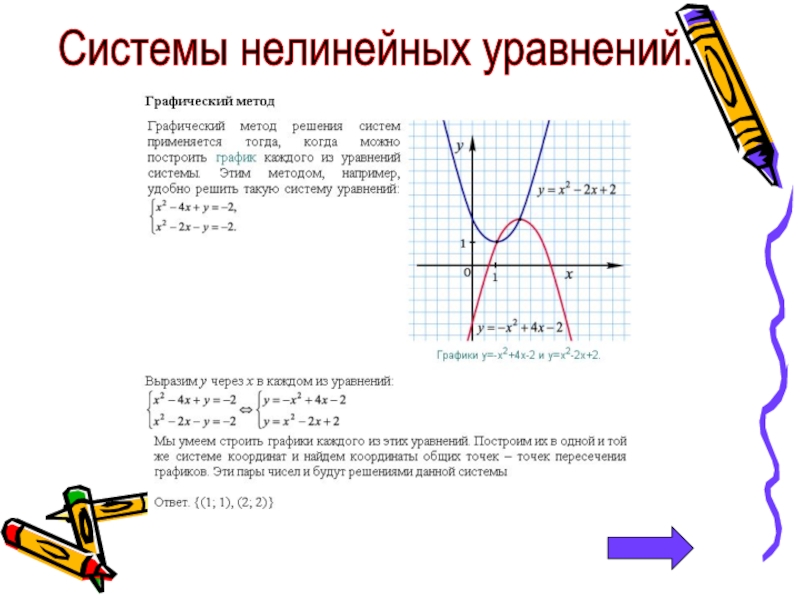
- 19. Системы нелинейных уравнений.
- 20. Оформление решения. Решение:
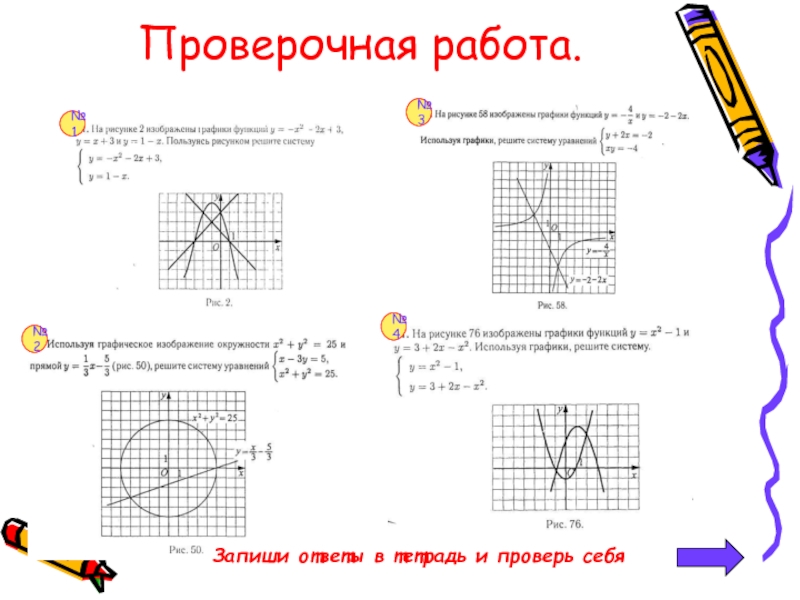
- 21. Проверочная работа. №1 №2 №3 №4 Запиши ответы в тетрадь и проверь себя
- 22. Проверь себя!
- 23. ДА! Перейди к следущему
- 24. НЕТ! Вернись обратно
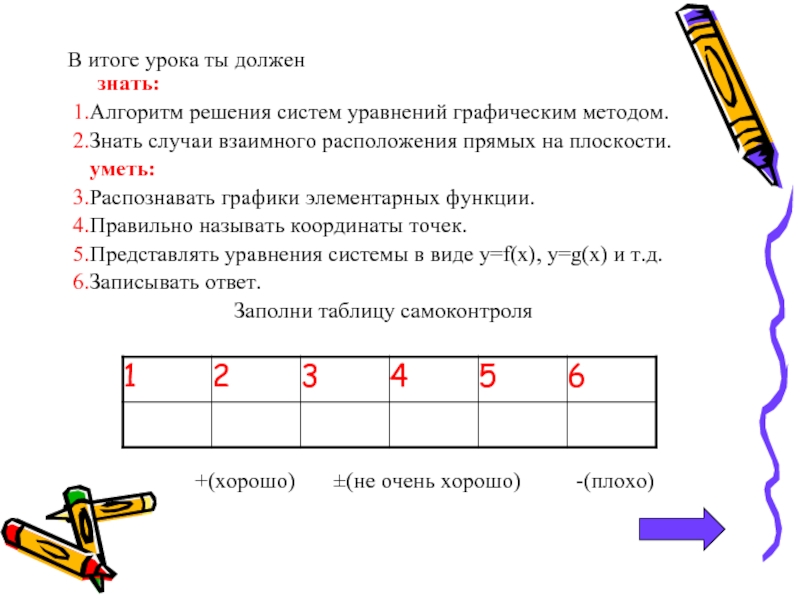
- 25. В итоге урока ты должен
- 26. СПАСИБО за работу!
План урока. 1.Актуализация знаний. 2.Системы линейных уравнений. 3.Нелинейные системы. 4.Отработка умений и навыков.
5.Итог урока.
Слайд 2План урока.
1.Актуализация знаний.
2.Системы линейных уравнений.
3.Нелинейные системы.
4.Отработка умений и навыков.
5.Итог урока.
Слайд 31.Повтори! ! !
1.Что называется системой уравнений?
2.Что называется решением системы?
3.Что значит решить
систему уравнений?
4Графический метод решения систем линейных уравнений.
4Графический метод решения систем линейных уравнений.
Слайд 4Теория темы.
Каждая пара значений переменных, которая является решением одновременно всех уравнений,
входящих в систему, называется ее решением.
Слайд 5Теория темы.
1.Системой уравнений называется некоторое количество уравнений, объединенных фигурной скобкой. Фигурная
скобка обозначает, что все уравнения должны выполняться одновременно.
Слайд 6Теория темы.
3.Решить систему уравнений –это значит найти все ее решения или
убедиться, что их нет.
Слайд 12Проверь себя !
ВЫБЕРИ ОТВЕТ
(2;6) (7;1) (2;6)
(7;1) (-3;-4) (2;6) (7;1) (-3;-4) другой
1
2
3
4
1
1
2
3
4
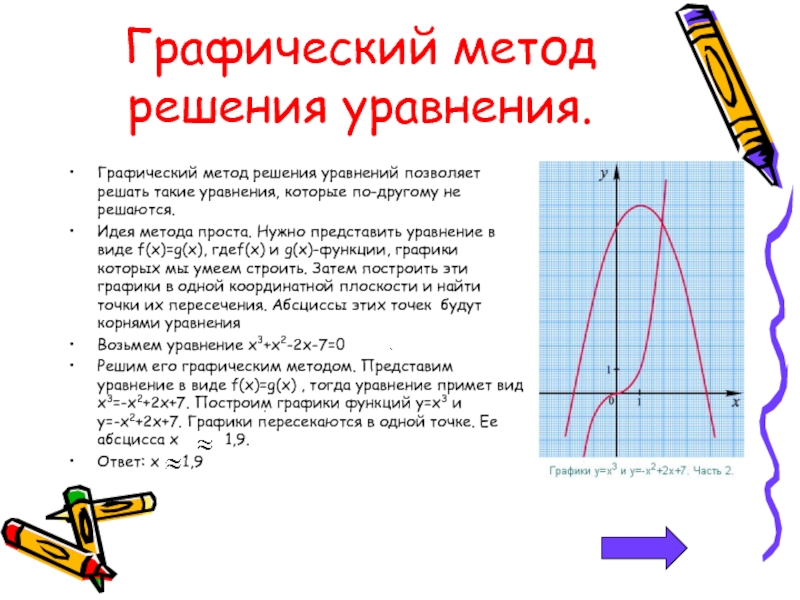
Слайд 15Графический метод решения уравнения.
Графический метод решения уравнений позволяет решать такие
уравнения, которые по-другому не решаются.
Идея метода проста. Нужно представить уравнение в виде f(x)=g(x), гдеf(x) и g(x)-функции, графики которых мы умеем строить. Затем построить эти графики в одной координатной плоскости и найти точки их пересечения. Абсциссы этих точек будут корнями уравнения
Возьмем уравнение x3+х2-2х-7=0
Решим его графическим методом. Представим уравнение в виде f(x)=g(x) , тогда уравнение примет вид х3=-х2+2х+7. Построим графики функций y=x3 и y=-x2+2x+7. Графики пересекаются в одной точке. Ее абсцисса х 1,9.
Ответ: х 1,9
Идея метода проста. Нужно представить уравнение в виде f(x)=g(x), гдеf(x) и g(x)-функции, графики которых мы умеем строить. Затем построить эти графики в одной координатной плоскости и найти точки их пересечения. Абсциссы этих точек будут корнями уравнения
Возьмем уравнение x3+х2-2х-7=0
Решим его графическим методом. Представим уравнение в виде f(x)=g(x) , тогда уравнение примет вид х3=-х2+2х+7. Построим графики функций y=x3 и y=-x2+2x+7. Графики пересекаются в одной точке. Ее абсцисса х 1,9.
Ответ: х 1,9
Слайд 16
Выбери ответ: (1;2), (-2;-1)
(1;2), (-2;-1) (-1;-2), (2;1) (1;2), (-2;-1) (-1;-2), (2;1) другой
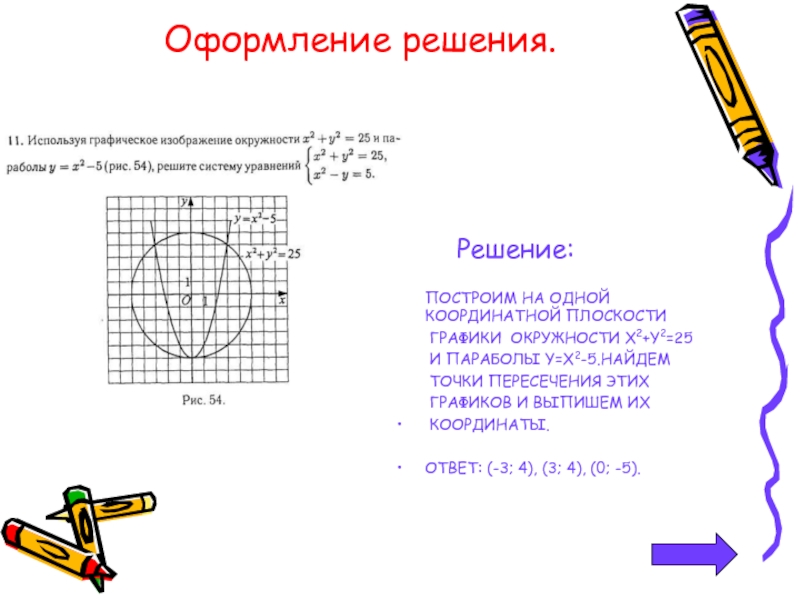
Слайд 20Оформление решения.
Решение:
ПОСТРОИМ НА ОДНОЙ КООРДИНАТНОЙ ПЛОСКОСТИ
ГРАФИКИ ОКРУЖНОСТИ
Х2+Y2=25
И ПАРАБОЛЫ Y=Х2-5.НАЙДЕМ
ТОЧКИ ПЕРЕСЕЧЕНИЯ ЭТИХ
ГРАФИКОВ И ВЫПИШЕМ ИХ
КООРДИНАТЫ.
ОТВЕТ: (-3; 4), (3; 4), (0; -5).
И ПАРАБОЛЫ Y=Х2-5.НАЙДЕМ
ТОЧКИ ПЕРЕСЕЧЕНИЯ ЭТИХ
ГРАФИКОВ И ВЫПИШЕМ ИХ
КООРДИНАТЫ.
ОТВЕТ: (-3; 4), (3; 4), (0; -5).
Слайд 25В итоге урока ты должен
знать:
1.Алгоритм решения систем уравнений графическим методом.
2.Знать случаи взаимного расположения прямых на плоскости.
уметь:
3.Распознавать графики элементарных функции.
4.Правильно называть координаты точек.
5.Представлять уравнения системы в виде y=f(x), y=g(x) и т.д.
6.Записывать ответ.
Заполни таблицу самоконтроля
+(хорошо) ±(не очень хорошо) -(плохо)
1.Алгоритм решения систем уравнений графическим методом.
2.Знать случаи взаимного расположения прямых на плоскости.
уметь:
3.Распознавать графики элементарных функции.
4.Правильно называть координаты точек.
5.Представлять уравнения системы в виде y=f(x), y=g(x) и т.д.
6.Записывать ответ.
Заполни таблицу самоконтроля
+(хорошо) ±(не очень хорошо) -(плохо)
