- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Симметрия в нашей жизни Геометрия презентация
Содержание
- 1. Симметрия в нашей жизни Геометрия
- 2. научить распознавать симметричные фигуры среди других;
- 3. Симметричность точек относительно прямой Симметричность фигуры относительно
- 4. “Симметрия (от греческого symmetria - «соразмерность») -
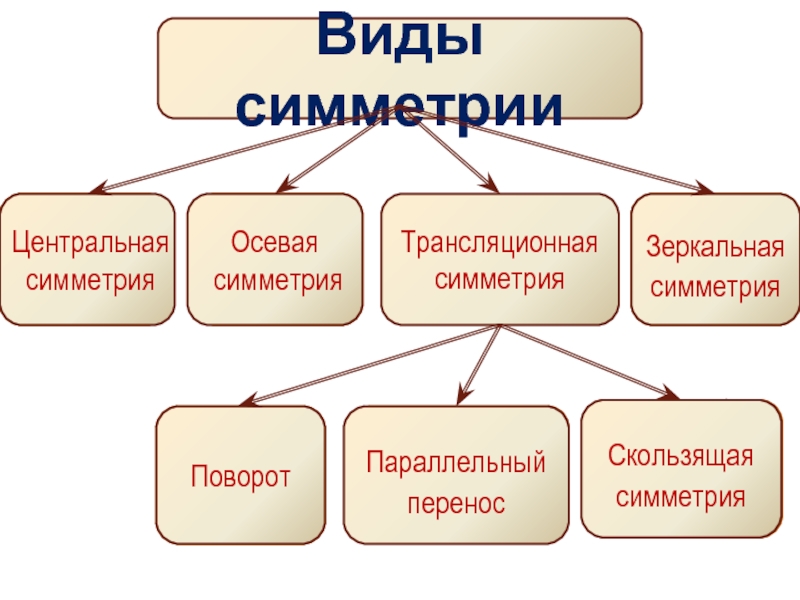
- 5. Виды симметрии Трансляционная симметрия Зеркальная симметрия Поворот Параллельный перенос Скользящая симметрия
- 6. Симметричность точек относительно прямой Определение
- 7. Симметричность фигуры относительно прямой Определение
- 8. Какие из данных фигур имеют ось симметрии?
- 9. Симметричность точек относительно точки Определение
- 10. Симметричность фигуры относительно точки Определение
- 11. Осевая симметрия
- 12. Центральная симметрия
- 13. Нетрадиционные виды симметрии Винтовая симметрия Симметрия поворота Переносная симметрия
- 14. Винтовая симметрия
- 15. Переносная симметрия или скользящее преобразование
- 16. Симметрия поворота
- 17. Симметрия в природе
- 18. Симметрия в архитектуре
- 19. Часто такую симметрию называют зеркальной. А зеркало
- 20. Предметы
- 21. Симметрия танца
- 22. Симметрия в литературе Палиндром - это абсолютное
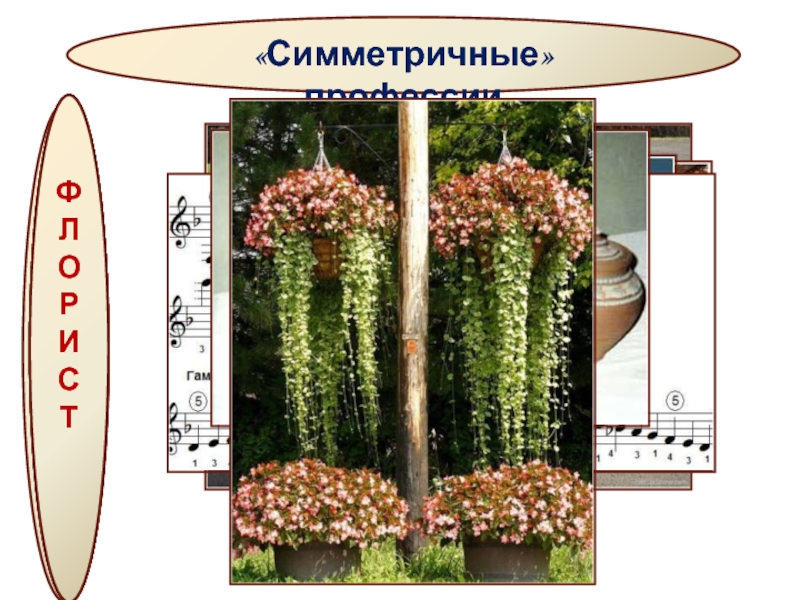
- 23. «Симметричные» профессии И Н Ж Е Н
- 24. Математики о симметрии Математик любит прежде всего
- 25. Заключение Симметрия играет огромную роль в
- 26. Ответьте на вопросы: С каким понятием мы
научить распознавать симметричные фигуры среди других; познакомить учащихся с использованием симметрии в природе, быту, искусстве, технике; развивать умения анализировать и сравнивать предметы; ЗАДАЧИ:
Слайд 2научить распознавать симметричные фигуры среди других;
познакомить учащихся с использованием симметрии
в природе, быту, искусстве, технике;
развивать умения анализировать и сравнивать предметы;
развивать умения анализировать и сравнивать предметы;
ЗАДАЧИ:
Слайд 3Симметричность точек относительно прямой
Симметричность фигуры относительно прямой
Симметричность точек относительно точки
Симметричность фигуры
относительно точки
Симметрия вокруг нас
Математики о симметрии
Симметрия вокруг нас
Математики о симметрии
Содержание
Слайд 4“Симметрия (от греческого symmetria - «соразмерность») - понятие, означающее сохраняемость, повторяемость,
«инвариантность» каких-либо особенностей структуры изучаемого объекта при проведении с ним определенных преобразований».
СИММЕТРИЯ
Слайд 5Виды симметрии
Трансляционная
симметрия
Зеркальная симметрия
Поворот
Параллельный перенос
Скользящая симметрия
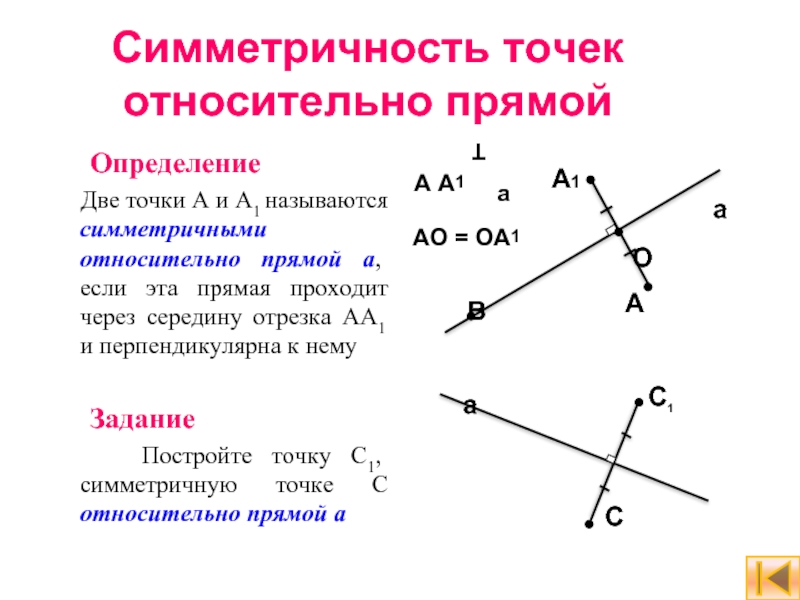
Слайд 6Симметричность точек относительно прямой
Определение
Две точки А и А1
называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему
Задание
Постройте точку C1, симметричную точке C относительно прямой а
Задание
Постройте точку C1, симметричную точке C относительно прямой а
A1
A
a
O
B
A A1
a
Т
AO = OA1
C1
a
C
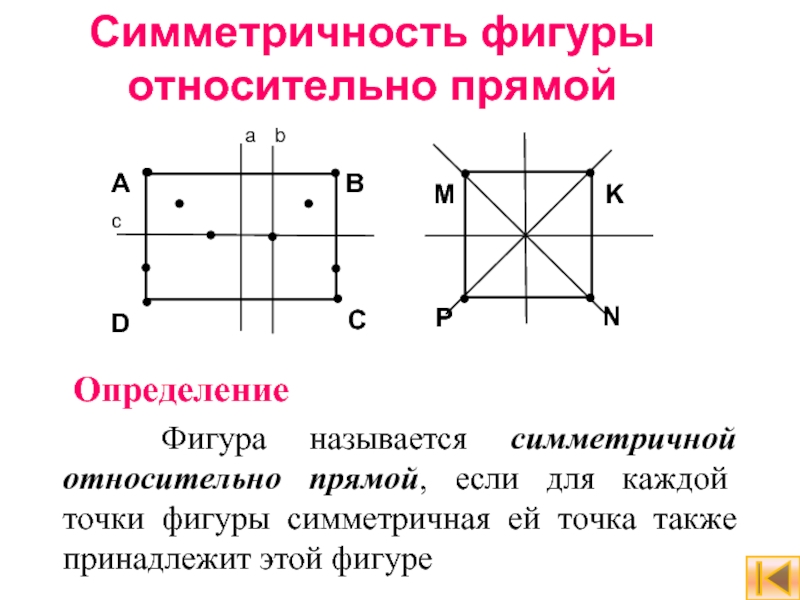
Слайд 7Симметричность фигуры относительно прямой
Определение
Фигура называется симметричной относительно прямой, если
для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре
А
D
B
C
M
K
N
P
a
b
c
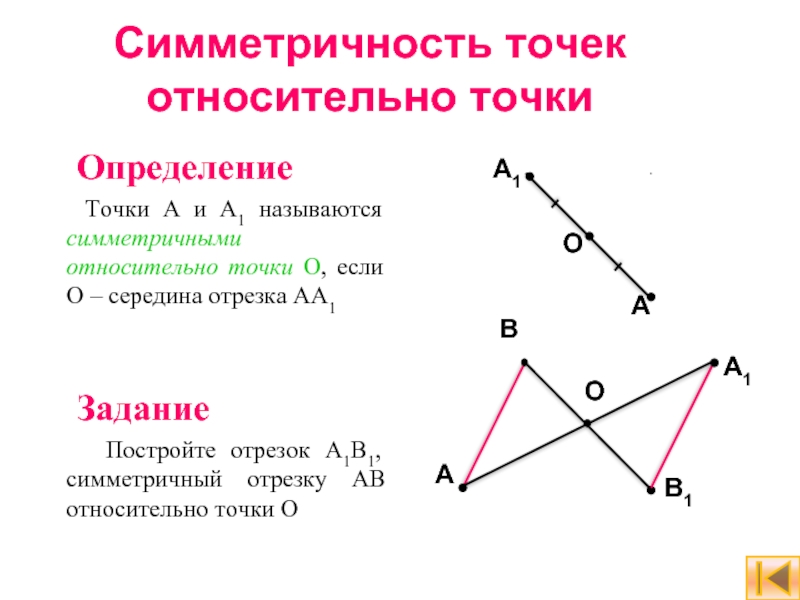
Слайд 9Симметричность точек относительно точки
Определение
Точки A и A1 называются симметричными
относительно точки О, если О – середина отрезка AA1
Задание
Постройте отрезок A1B1, симметричный отрезку AB относительно точки О
Задание
Постройте отрезок A1B1, симметричный отрезку AB относительно точки О
A
O
A
B
B1
O
A1
A1
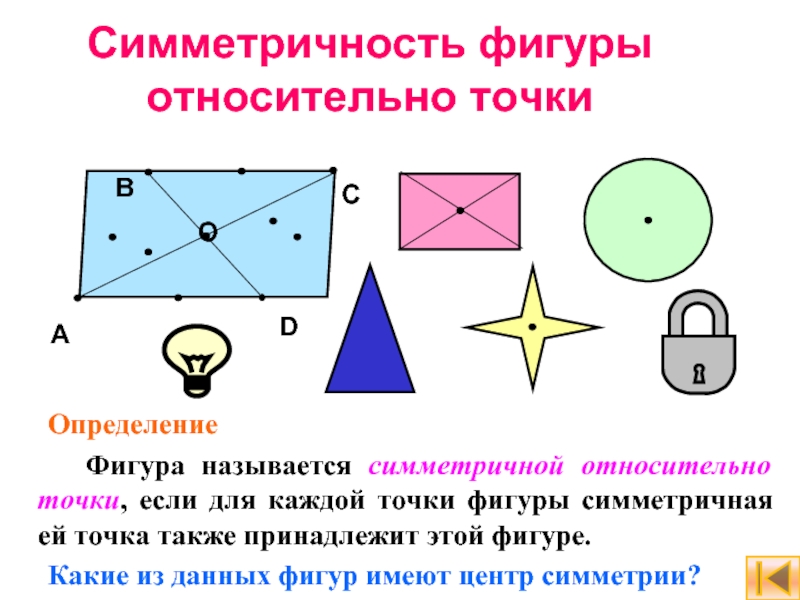
Слайд 10Симметричность фигуры относительно точки
Определение
Фигура называется симметричной относительно точки,
если для каждой точки фигуры симметричная ей точка также принадлежит этой фигуре.
Какие из данных фигур имеют центр симметрии?
Какие из данных фигур имеют центр симметрии?
A
B
C
D
O
Слайд 19Часто такую симметрию называют зеркальной. А зеркало не просто копирует объект,
но и меняет местами передние и задние части объекта по отношению к зеркалу.
Дубаи Башни Эмиратов
Соловецкий монастырь
Германия Гамбург
Слайд 22Симметрия в литературе
Палиндром - это абсолютное проявление симметрии в литературе. Например:
«А луна канула»,
«А роза упала на лапу Азора».
Палиндром В.Набокова:
Я ел мясо лося, млея...
Рвал Эол алоэ, лавр.
Те ему: "Ишь! И умеет Рвать!"
Он им: "Я - минотавр!"
назад
Слайд 24Математики о симметрии
Математик любит прежде всего симметрию
Максвелл Д.
Красота тесно связана с симметрией
Вейль Г.
Симметрия … является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство
Вейль Г.
Для человеческого разума симметрия обладает, по - видимому, совершенно особой притягательной силой
Фейнман Р.
Красота тесно связана с симметрией
Вейль Г.
Симметрия … является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство
Вейль Г.
Для человеческого разума симметрия обладает, по - видимому, совершенно особой притягательной силой
Фейнман Р.
Слайд 25Заключение
Симметрия играет огромную роль в искусстве: в архитектуре, в музыке,
в поэзии; природе: у растений и животных; в технике, в быту.
Слайд 26Ответьте на вопросы:
С каким понятием мы сегодня познакомились?
Какие виды симметрии вы
запомнили?
Что нового вы узнали?
