- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение задач С4 презентация
Содержание
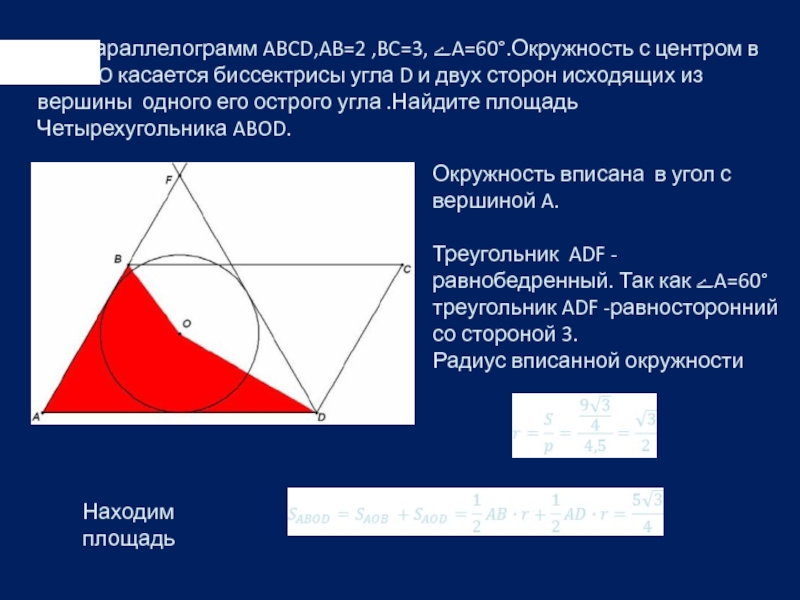
Слайд 2 Дан параллелограмм ABCD,AB=2 ,BC=3, ﮮA=60°.Окружность с центром в
Окружность вписана в угол с вершиной A.
Треугольник ADF -равнобедренный. Так как ﮮA=60° треугольник ADF -равносторонний со стороной 3.
Радиус вписанной окружности
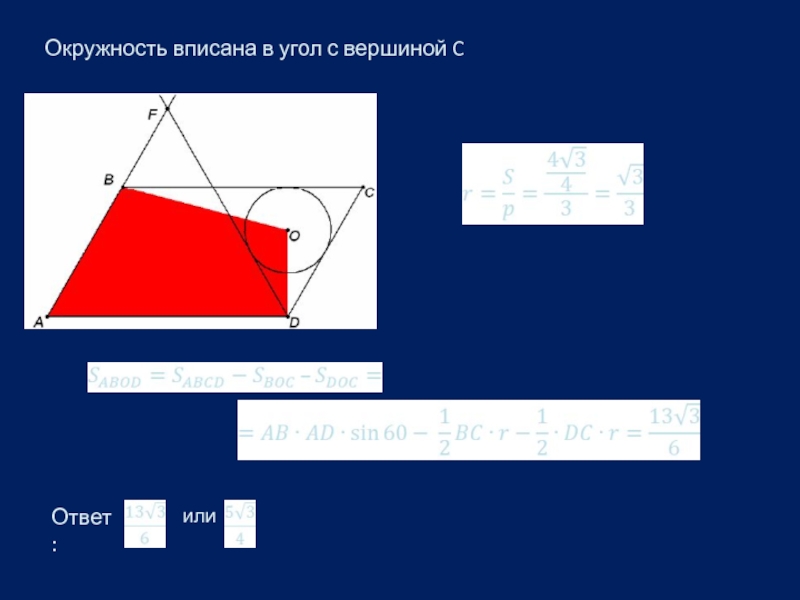
Находим площадь
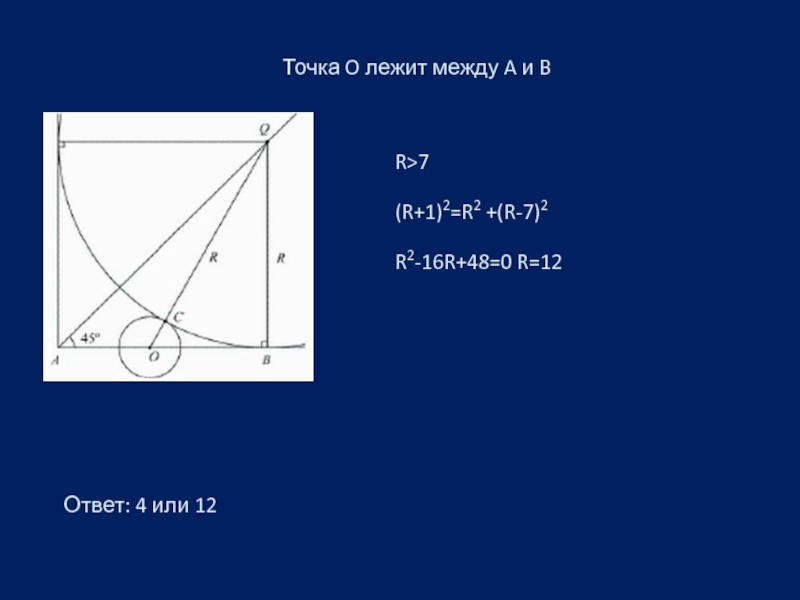
Слайд 4 На стороне прямого угла с вершиной A взята точка O, причем AO = 7.
Пусть Q –центр искомой окружности радиуса R, B-точка касания этой окружности со стороной AO,C- точка касания окружностей. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла, значит, BAQ=45. Тогда AB=QB=R. Линия центров двух касающихся окружностей проходит через точку их касания, поэтому OQ=OC+CQ=1+R.
Точка B лежит между A и O.Тогда R<7.По теореме Пифагора OQ2 =QB2+OB2 или, (1+R)2=R2+(7-R)2.
R2-16R+48=0 , а так как R<7 ,то R=4.
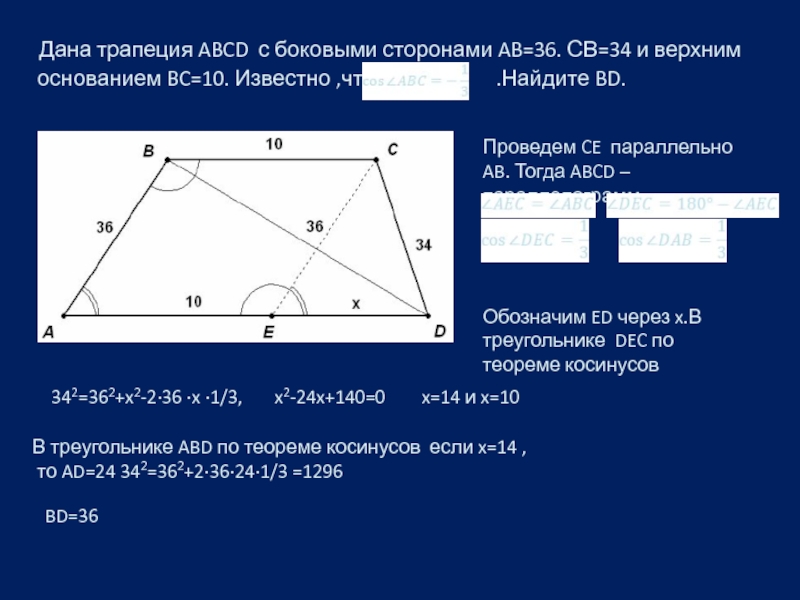
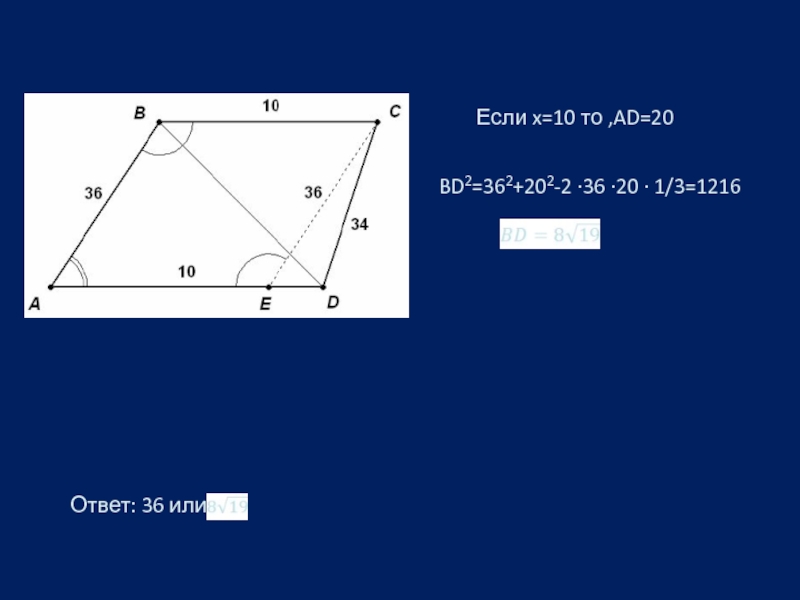
Слайд 6 Дана трапеция ABCD с боковыми сторонами AB=36. СВ=34 и
Проведем CE параллельно AB. Тогда ABCD – параллелограмм.
Обозначим ED через x.В треугольнике DEC по теореме косинусов
342=362+x2-2∙36 ∙x ∙1/3, x2-24x+140=0 x=14 и x=10
В треугольнике ABD по теореме косинусов если x=14 ,
то AD=24 342=362+2∙36∙24∙1/3 =1296
BD=36