Ratios презентация

Содержание

Statistical Indicators Statistical indicator is a numeric characteristic of social and economic processes. All indicators can be classified as individual and summary

Слайд 1Ratios
Lecture, the 22d of February

Слайд 2Statistical Indicators


Statistical indicator is a numeric characteristic of social and economic

processes.
All indicators can be classified as individual and summary


Слайд 3 Individual & Summary
Individual indicators characterize only one unit of population
Summary

indicators characterize one class of population or the whole population

Слайд 4Individual & Summary
Summary
Individual

Слайд 5Individual
Individual absolute value characterizes one unit of the population investigated. It

reflects the size of quantitative traits in individual units of the studied population.

Individual absolute values are obtained in the process of statistical observation and characterize the individual units of a population (a man's height, weight, volume of production, etc.)

Слайд 6Summary
The summary, or total absolute value characterizes the group of

units together, or population as a whole. It expresses the size, amount of quantitative traits in the whole studied population.
Summary indicator gives us the characteristic size of the phenomenon analyzed on a given set of objects or any part of the set. The total values are obtained by direct counting of units of observation or as a result of summation of the values of quantitative traits, which have a unit (for example, the population of the country, a separate branch of production).

Слайд 7Individual & Summary
When we study wages the individual absolute indicator is

a specific amount of wage for each worker, and the summary absolute value is the wages fund for the entire company, for some classes of workers or the payroll of a structural unit (for example, the first shop)
Summary indicators can also be classified as volumetric and calculated



Слайд 8 Volumetric & Calculated
Volumetric indicators are received by adding values

of population separate units
Calculated indicators can be received by making different calculations
All indicators can also be classified as absolute, ratio and average


Слайд 9 Absolute, Ratio & Average
Absolute indicators are measured in natural

units (ton, kg, meter), cost units (USD, ruble, euro), and labour units (man-hour, man-day)
Absolute values are the basis for the calculation of various statistical ratios
Average indicators will be described in the next lecture


Слайд 10Example 1 302. What is it? Possible answers: a) The date –

the 2nd of March; b) personal number of Dalaloyan Anait; c) a digital; г) a number; d) population of Surgut on the 1st of January, 2010; e) something else – point out

Слайд 111.Absolute indicators
In statistics, bare numbers can not exist without a specific

reference to the unit of measurement, time and place

Слайд 12 Ratios

Слайд 13Ratio

Any relative value is the result of comparison of two

variables 
Ratio, or relative indicator RI represents the result of dividing one absolute indicator A by another B and expresses a ratio between two quantitative indicators

Слайд 14Ratio


RI=A/B

Слайд 15Ratios

The ratio of quantities A and B can be expressed

as:
the ratio of A to B
as B is to A
A:B.
The quantities A and B are sometimes called terms with A being the antecedent and B being the consequent

Слайд 16Ratios

The proportion expressing the equality of the ratios A:B and

C:D is written A:B=C:D or A:B::C:D.
Again, A, B, C, D are called the terms of the proportion. A and D are called the extremes, and B and C are called the means. The equality of three or more proportions is called a continued proportion

Слайд 17Ratios

A ratio that has integers for both quantities and that

cannot be reduced any further (using integers) is said to be in simplest form or lowest terms
Sometimes it is useful to write a ratio in the form   1:n or n:1    to enable comparisons of different ratios.
For example, the ratio 4:5 can be written as   1:1.25 (dividing both sides by 4)
Alternatively, 4 : 5 can be written as  
0.8: 1   (dividing both sides by 5)

Слайд 18Ratios

Where the context makes the meaning clear, a ratio in

this form is sometimes written without the 1 and the colon, though, mathematically, this makes it a factor or multiplier

Слайд 19Ratios

Ratios express numeric relation specific to particular social phenomena or

processes. 
The indicator A is called compared value. The indicator B, that is compared with indicator A, is called the base or a base of comparison.
  When both indicators namely A and B have the same unit of measure, the result is expressed in coefficient (e.g. 0.3), percentage (30%) or per mil (from Latin pro mille) (300 ‰) 

Слайд 20Ratios

In mathematics, a ratio expresses the magnitude of quantities relative

to each other. Specifically, the ratio of two quantities indicates how many times the first quantity is contained in the second and may be expressed algebraically as their quotient

Слайд 21Quotient

A quotient is the result of a division. For example, when dividing

6 by 3, the quotient is 2, while 6 is called the divident, and 3 the divisor. The quotient can also be expressed as the number of times the divisor divides into the dividend.
A quotient can also mean just the integer part of the result of dividing two integers. For example, the quotient of 13 ÷ 5 would be 2 while the remainder would be 3

Слайд 22Properties of Ratio
Ratio shows how many times the compared value A is

more or less than the base B, or what proportion of A is in relation to B. In some cases, the relative value indicates how many units of A corresponds per unit of B.
Another important property - the ratio abstracts from absolute values and allows to compare indicators, the absolute amounts of which are not directly comparable

Слайд 23Expression forms of ratios

Слайд 24Expression forms of ratios
A comparison of the absolute values with the

same name gives us unnamed ratios. They can be expressed in the form of shares, times, percentages, per mils, etc.
A comparison of values with different names gives us named ratios. Their name is formed as combination of the names of A and B. The choice of form depends on the nature of analytical problems: just to express the ratio most clearly

Слайд 25Simple Division
RI=A/B
This case of Ratio shows:
1 - how many times

the compared value A is more or less than the base B
2 - what proportion of A is in relation to B
3 - in some cases, the Ratio indicates how many units of A corresponds per unit of B


Слайд 26Percentage
RI=A*100/B
To switch from % to coefficient, RI should be divided by

100
To obtain % from coefficients, we’ll multiply RI by 100

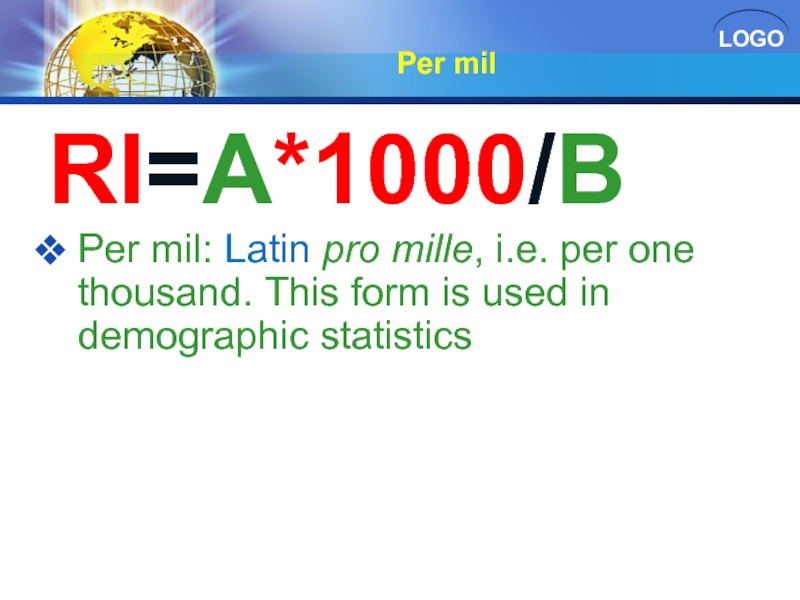
Слайд 27Per mil
RI=A*1000/B
Per mil: Latin pro mille, i.e. per one thousand. This

form is used in demographic statistics

Слайд 28Examples of Ratio
The quantities being compared in a ratio might be

physical quantities such as speed, or may simply refer to amounts of particular objects. A common example of the latter case is the weight ratio of water to cement used in concrete, which is commonly stated as 1:4. This means that the weight of cement used is four times the weight of water used. It does not say anything about the total amounts of cement and water used, nor the amount of concrete being made

Слайд 29Display parameters



The ratio of width to height of typical computer displays
Older

televisions have a 4:3 ratio which means that the height is 3/4 of the width. Widescreen TVs have a 16:9 ratio which means that the width is nearly double the height

Слайд 30Per mil
RI=A*1000/B
To pass from per mil to coefficients, RI should be

divided by 1000
To obtain per mil from coefficients, multiply RI by 1000
To go from per mil to per cent, RI divide by 10
To move from per cent to per mil, multiply RI by 10

Слайд 31There are seven kinds of ratios

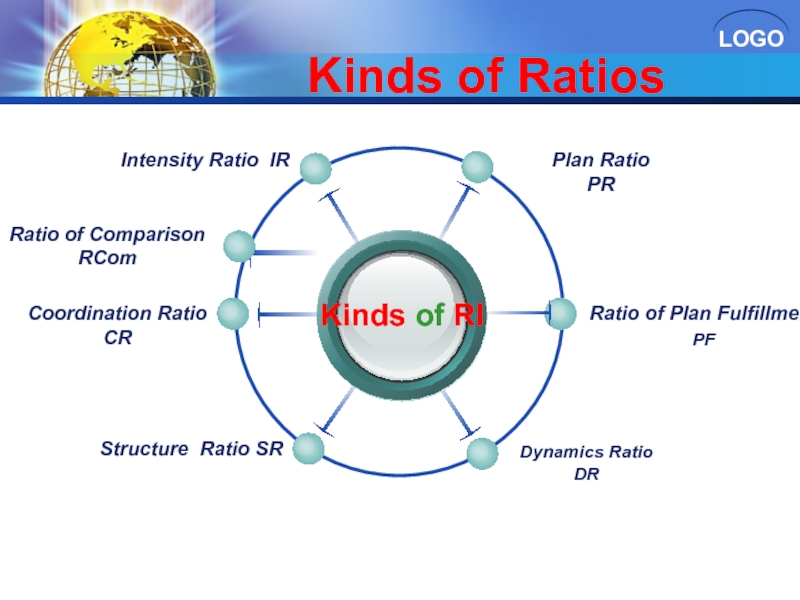
Слайд 32Kinds of Ratios










Kinds of RI
Plan Ratio
PR
Intensity Ratio IR
Ratio of Plan

Fulfillment
PF

Dynamics Ratio
DR

Coordination Ratio
CR

Structure Ratio SR



Ratio of Comparison
RCom

Слайд 33Ratio of Plan target RP
Plan Ratio PR is a ratio between

the planned value of future period and real achieved level of basic period (the previous or past or base value):





where - plan indicator;

- real level of basic period


Слайд 34PR
Plan Ratio is the ratio between the value of indicator set

at the planned period and the value of indicator achieved by the planned period or by the period taken as the basis of comparison
PR is expressed in coefficients or percentages after additional multiplication by 100%
In case of coefficients PR shows by how many times the plan is larger or smaller than achieved values by the planned period
In case of percentage PR shows by how many percent the planned value is larger or smaller than the actual value in previous or past value



Слайд 35PF
Ratios of plan fulfillment PF characterize the extent of accomplishment of

plan target
PF is the ratio between the current or reporting value and the planned value :


where - achieved indicator ;
- planned indicator.
It shows how the plan has been fulfilled




Слайд 36

DR

Dynamics Ratio or Time Ratio DR – represents the ratio of values of the same indicator during different periods of time). It is a ratio between the current or reporting value x1 and the past or base meaning x0 and expressed in percentages



where x1 – real, achieved indicator ;
x0 – basic indicator.

There are two kinds of DR – chain and basic


Слайд 37Basic DR
Basic ratio of dynamics – ratio between the value of

indicator of current period and the value considered as the basis of comparison


where x1 – current level;
x0 – basic level

Слайд 38Chain DR
Chain ratio of dynamics – ratio between the current value

and the past period value. Shows the change of the indicator from one period to another or from one moment of time to another.



where xi – current level;
xi-1 – previous adjacent level

Слайд 39Chain method
While using chain calculation method we should compare each consequent

level with the previous adjacent.
Time series analysis indicates its levels by letter Y instead of X

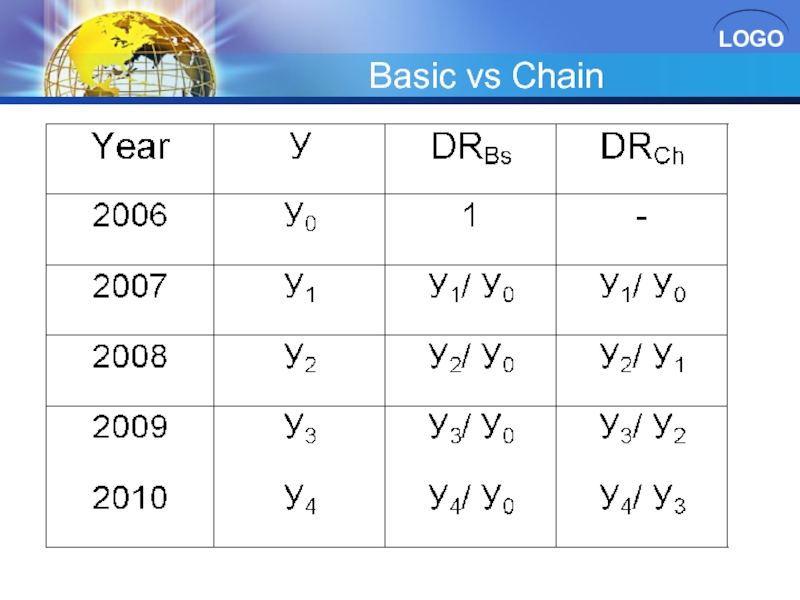
Слайд 40Basic vs Chain

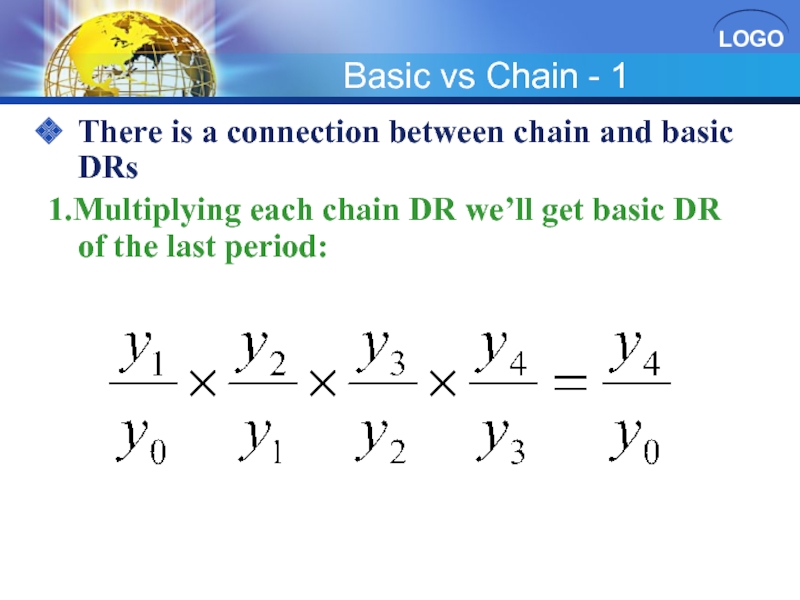
Слайд 41Basic vs Chain - 1
There is a connection between chain and

basic DRs
1.Multiplying each chain DR we’ll get basic DR of the last period:



Слайд 42Basic vs Chain - 2
2.Dividing the following basic DR by the

previous DR we’ll get the chain DR of the following period:

Слайд 43Basic vs Chain - 3
3. Dividing the following basic DR by

the chain DR of the same period we will get the previous basic DR:

Слайд 44Example 3
The sale of cotton fabric by a section of department

store in January totaled 3,956,000 rubles, in February – 4,200,000 rubles, in March – 4,700,000 rubles

Слайд 45Example 1
Rates of growth
Basic DRs (basis – level of sales in

January)
DRF/J = 4200 * 100% =106,3%
3950
DRMJ = 4700 * 100% =118,9%
3950
Chain RDs
DRF/J = 4200 * 100% =106,3%
3950
DRM/F = 4700 * 100% =111,9%
4200

Слайд 46Correlation of 3 ratios

DR = PR * PF

Слайд 47Example 2
In the third quarter the turnover was 150 million rubles.

Plan for the fourth quarter was 180 million rubles. Real turnover in the fourth quarter was 202,5 million rubles. Calculate DR, PR, PF and show their interconnection

y0=150;
y1pl=180;
y1=202,5




Слайд 48Example 2

Слайд 49Example 2

Interconnection of DR, PR & PF:

DR= PR* PF

1,35 =1,2 х

1,125

Слайд 50Example 3
The increase of the output of a branch during 2010

was planned to be 7.5%. Real increase during 2010 was 109,5%. Determine the ratio of plan fulfillment of the output.

PF = 109,5 * 100% = 102%
107,5

Слайд 51Ratio of comparison RCom

Слайд 52RCom

Ratio of comparison is the ratio of similar indicators related

to different objects. RCom is a ratio between two identical characteristics describing
different populations:

Слайд 53Example 4

The water reserves in Lake Baikal - 23000 cu. km, and

in Lake Ladoga 911cu. km

Слайд 54Example 4
Another way is to calculate a share in per cent,

it gives us an idea of the next ratio

Слайд 55Structure Ratio SR

Слайд 56 SR

Structure Ratio is a ratio of parts and the whole

characterizing the structure of the population, i.e. a share of each part in the population. SR is expressed in unit shares or in per cent:




The sum of SRs calculated for all parts of a population is equal to 1 or 100% depending on the unit of measure

Слайд 57 Example 5
The total number of Russian population at the beginning of

2009 was  equal to 141.9 million, 103.7 million were urban residents, 38.2 million - rural. Calculating SR, we can determine the structure of the population by place of residence:



Слайд 58Intensity Ratio IR

Слайд 59IR
Intensity Ratio IR shows how much a process under analysis is

spread (birth rate, death rate, GDP per capita). IR characterizes the distribution of the process in a certain environment (density, intensity of a certain event)

Слайд 60IR
Intensity Ratio IR is always a ratio of absolute values with

different units of measure. For instance density of population in persons per one km² we receive dividing number of population in thousands by square in thousand km²:
population density = the total number of people / area of land (measured in km² or sq miles)

Слайд 61IR
IR is the ratio of different indicators relating to the

same object

Слайд 62 Example 6
Number of retailers in the region at the end of

the year was 6324. The population of the region on the same date amounted to 234.2 thousand. 
IR = 6324 * 10 000 / 234 200 = 27.003                  Unit of measure – number of retailers per 10 thousand people living in the region

Слайд 63IR
IR characterizes the distribution of the process in a certain environment
For

example, production per capita is calculated as the ratio of annual production by the average annual population, the fertility rate is obtained by dividing the number of births during a year by the average number of women in the fertility age (15-49 years)

Слайд 64Coordination Ratio CR

Слайд 65Coordination Ratio CR

CR is a ratio between two parts of one

population




Слайд 66 CR

Coordination Ratio is the ratio of parts of the whole

between each other

RC = Part of the whole/ Another part of the same population

CR is put into times or unit shares. Multiplication by 10 and 100 is allowed if logic requires that – there cannot be a ratio between people: 1 to 1.5, there can be 10 to 15



Слайд 67RC

RC is used for additional characteristic of structure (e.g. number of

women for per 1000 men and vice versa)

Слайд 68 Example 7
At the beginning of the year the number of employees

with higher education working in “Trade house” association was equal to 53, while the number of employees with specialized secondary education was 106



Слайд 69 Example 7
Принимаем за базу сравнения численность специалистов с высшим образованием: We

take the number of employees with higher education as the base of comparison

RC = 106 / 53 = 2.0 : 1.0,

i.e. for every two employees with specialized secondary education there is one with higher education

Слайд 70 Ratio of level of economic development LED

Слайд 71LED ratio

Ratio of level of economic development characterizes the size of

different types of production per capita
It characterizes the size of output per capita. We put “capita” in the denominator – average population size

Слайд 72 LED ratio

LED ratio is a case of intensity ratio

Слайд 73Your Task 3
1.Send a request for a Ratio Puzzle on email

asidenko@fa.ru1.Send a request for a Ratio Puzzle on email asidenko@fa.ru or oknedis@bk.ru
2.Solve the puzzle: explain all calculations below the table
3.The number of points is equal to the number of cells filled (number of steps described below the table)

Слайд 74Task 3
4. Bonuses:
If you think the puzzle has no solution you

add a desirable number to any empty cell and add 10 points for each wrong cell
You may invent a new ratio puzzle and get a prize of minimum 50 points
5.Calculate the total desired number of your points gained
6.Send solved puzzle to my email

Слайд 75www.themegallery.com
Thank You !
www.themegallery.com

Похожие презентации

Наиболее характерные неисправности магнитных пускателей 251
ФСК Факел 233
Цена вопроса 212
Техники снижения нервно -психологического напряжения и 203
Дніпро 738
Загадочный танграм. 319

Обратная связь

Если не удалось найти и скачать презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть 

Что такое ThePresentation.ru?

Это сайт презентаций, докладов, проектов, шаблонов в формате PowerPoint. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами с другими пользователями.

Для правообладателей

Яндекс.Метрика