Владимир Владимирович Писляков
нач. отдела информационных систем
и электронных ресурсов библиотеки ГУ-ВШЭ, Москва
http://library.hse.ru
pislyakov@hse.ru
SCIENCE ONLINE: электронные информационные ресурсы для науки и образования
Турция, 2005
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
РАСПРЕДЕЛЕНИЕ БРЭДФОРДАИ ПОДОБНЫЕ ЕМУИНФОМЕТРИЧЕСКИЕ ЗАКОНЫна примере статистики использованияэлектронных ресурсов в университетской библиотеке презентация
Содержание
- 1. РАСПРЕДЕЛЕНИЕ БРЭДФОРДАИ ПОДОБНЫЕ ЕМУИНФОМЕТРИЧЕСКИЕ ЗАКОНЫна примере статистики использованияэлектронных ресурсов в университетской библиотеке
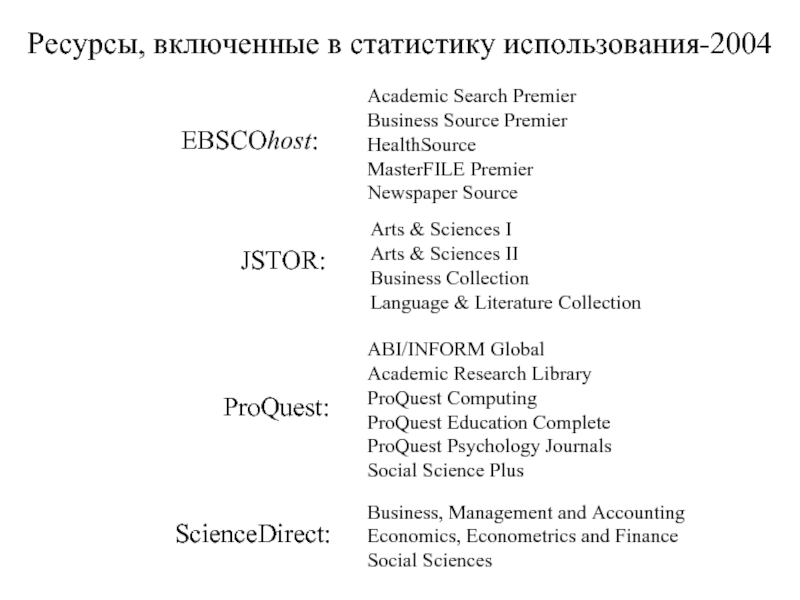
- 2. Academic Search Premier Business Source Premier HealthSource
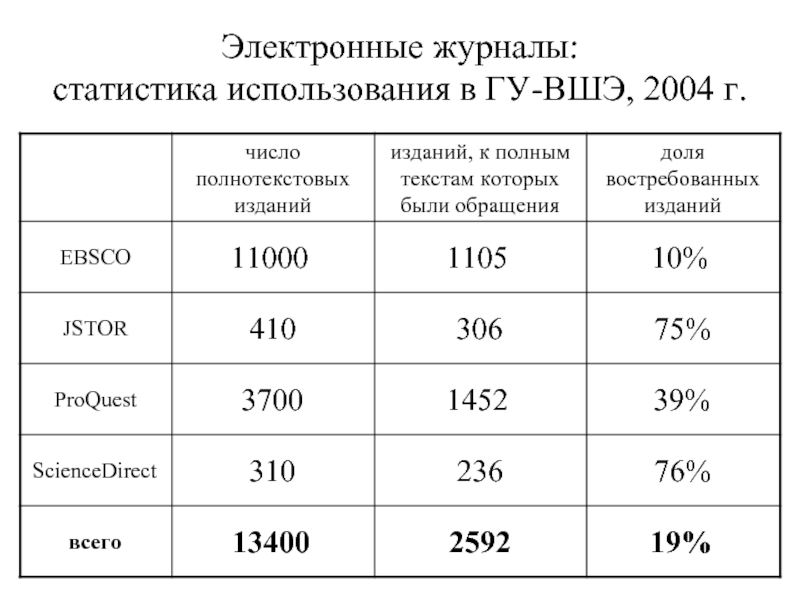
- 3. Электронные журналы: статистика использования в ГУ-ВШЭ, 2004 г.
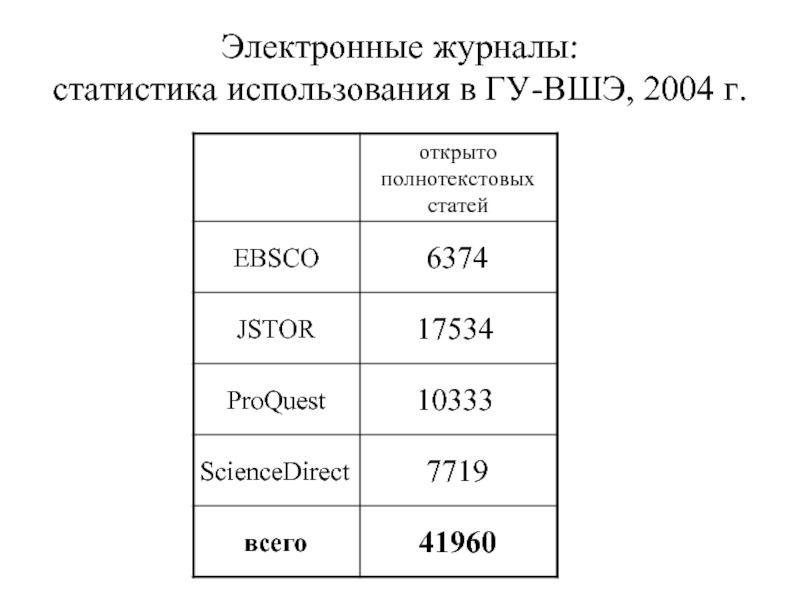
- 4. Электронные журналы: статистика использования в ГУ-ВШЭ, 2004 г.
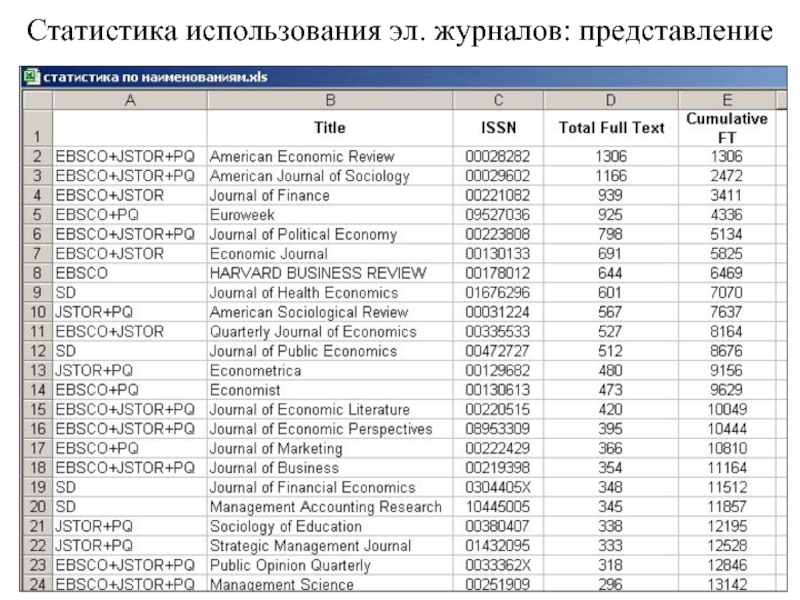
- 5. Статистика использования эл. журналов: представление
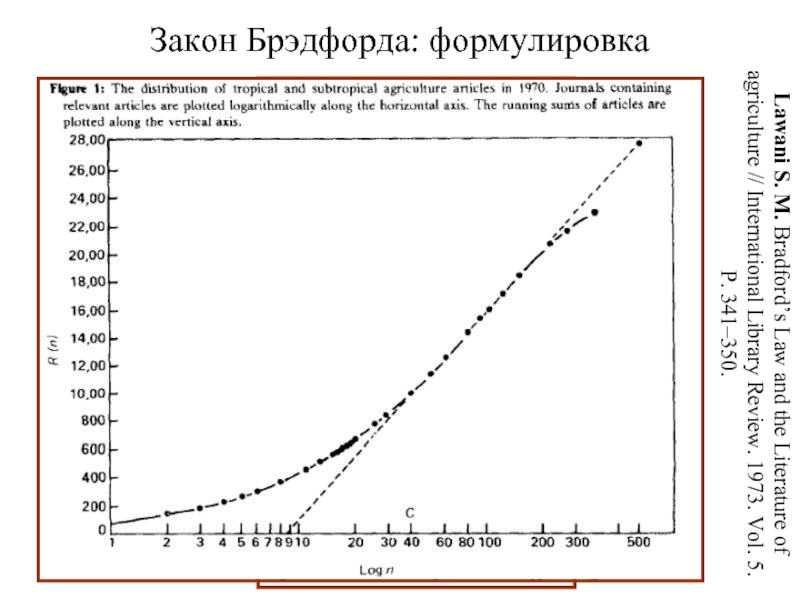
- 6. Закон Брэдфорда: формулировка Bradford S. C. Sources
- 7. 26 журналов — 13987 статей 139 журналов — 13975
- 8. Закон Брэдфорда: проверка на статистике ГУ-ВШЭ
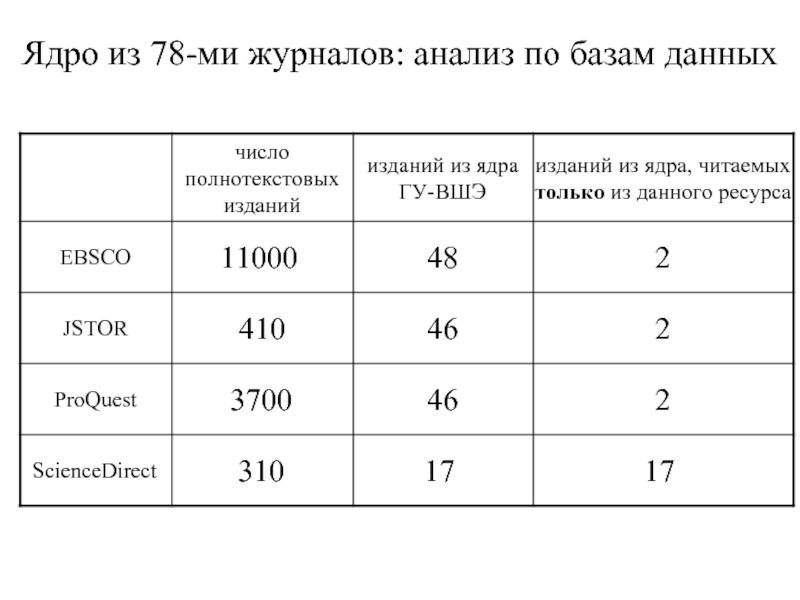
- 9. Ядро из 78-ми журналов: анализ по базам данных
- 10. Закон Леймкулера: формулировка Leimkuhler F. F. The
- 11. Используем нелинейную регрессию и пытаемся, подбирая коэффициент
- 12. Закон Лотки: формулировка Lotka A. J. The
- 13. Приложение закона к статистике использования электронных ресурсов:
- 14. Закон Ципфа: формулировка Zipf G. K. The
- 15. Приложение закона к статистике использования электронных ресурсов:
- 16. Pareto V. Cours d’Économie Politique. Vol. 2.
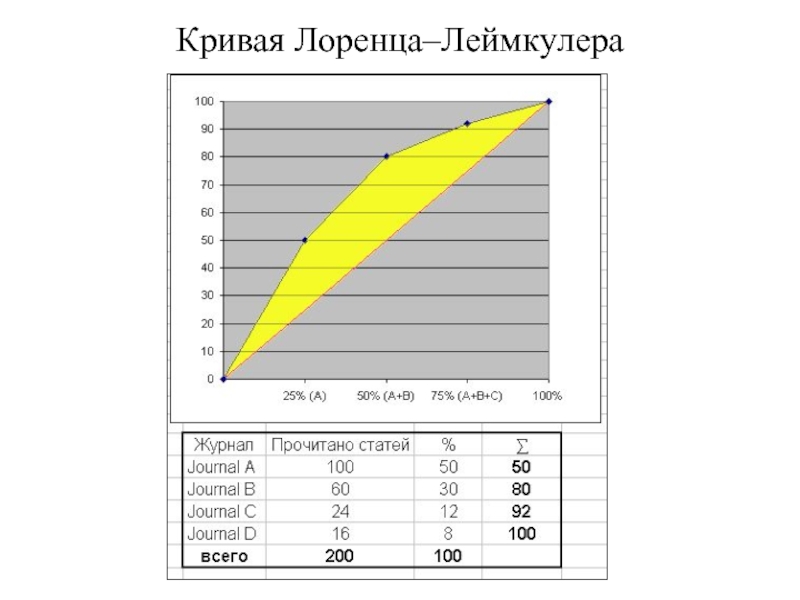
- 17. Кривая Лоренца–Леймкулера
- 18. Приложение закона к статистике использования электронных ресурсов:
- 19. Кривая Лоренца-Леймкулера и индекс Джини по статистике
- 20. Bookstein A. Informetric Distributions, part I: Unified
- 21. РАСПРЕДЕЛЕНИЕ БРЭДФОРДА И ПОДОБНЫЕ ЕМУ ИНФОМЕТРИЧЕСКИЕ ЗАКОНЫ
Слайд 1РАСПРЕДЕЛЕНИЕ БРЭДФОРДА И ПОДОБНЫЕ ЕМУ ИНФОМЕТРИЧЕСКИЕ ЗАКОНЫ на примере статистики использования электронных ресурсов в университетской
Слайд 2Academic Search Premier
Business Source Premier
HealthSource
MasterFILE Premier
Newspaper Source
ABI/INFORM Global
Academic Research Library
ProQuest Computing
ProQuest
Arts & Sciences I
Arts & Sciences II
Business Collection
Language & Literature Collection
EBSCOhost:
ProQuest:
JSTOR:
Ресурсы, включенные в статистику использования-2004
ScienceDirect:
Business, Management and Accounting
Economics, Econometrics and Finance
Social Sciences
Слайд 6Закон Брэдфорда: формулировка
Bradford S. C. Sources of information on specific subjects
Bradford S. C. Documentation. London: Crosley Lockwood, 1948 (Washington: Public Affairs Press, 1950).
429 статей
в 9 журналах
499 статей
в 59 журналах
404 статьи
в 258 журналах
Lawani S. M. Bradford’s Law and the Literature of agriculture // International Library Review. 1973. Vol. 5. P. 341–350.
Слайд 726 журналов — 13987 статей
139 журналов — 13975 статей
2427 журналов — 13998 статей
139 :
2427 : 139 = 17,5
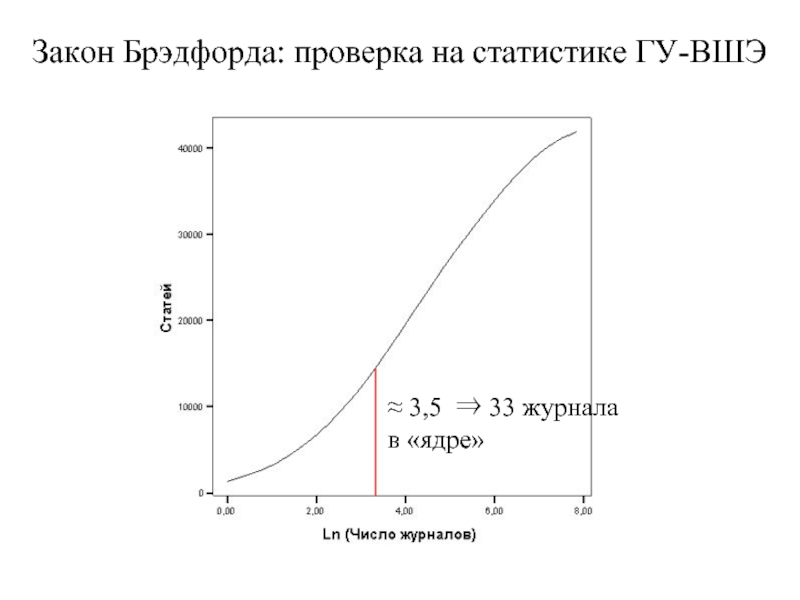
≈ 3,5 ⇒ 33 журнала в «ядре»
Закон Брэдфорда: проверка на статистике ГУ-ВШЭ
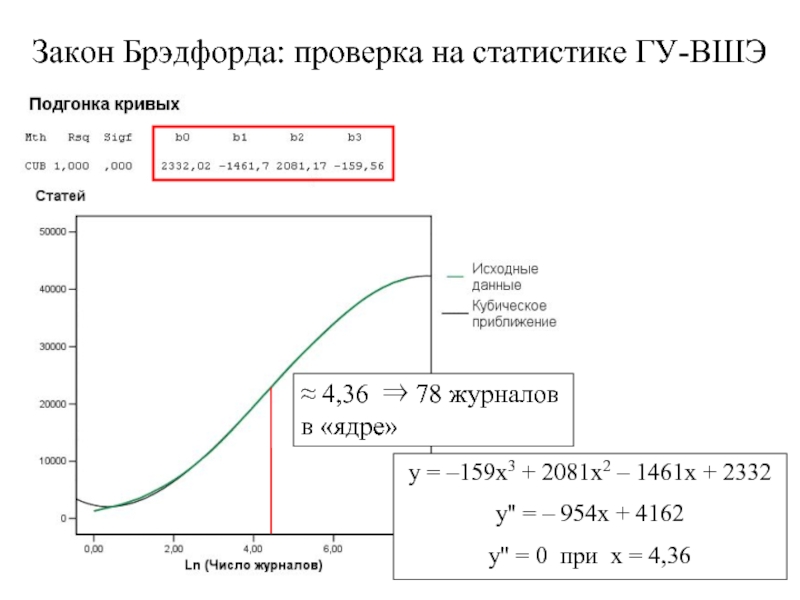
Слайд 8Закон Брэдфорда: проверка на статистике ГУ-ВШЭ
y = –159x3 + 2081x2 –
y'' = – 954x + 4162
y'' = 0 при x = 4,36
≈ 4,36 ⇒ 78 журналов в «ядре»
Слайд 10Закон Леймкулера: формулировка
Leimkuhler F. F. The Bradford Distribution // Journal of
Y = A ln(1 + BN)
Y — число статей в N наиболее продуктивных журналах;
A и B — некоторые коэффициенты
Для нормированных величин:
Y = ln(1 + βx) / ln(1 + β)
Y — доля от общего числа статей в доле x наиболее продуктивных журналов;
β — «коэффициент концентрации»
2500
42000
0
журналы
статьи
1
1
0
доля
журналов
доля
статей
кривая Леймкулера:
Слайд 11Используем нелинейную регрессию и пытаемся, подбирая коэффициент β, приблизить наш график
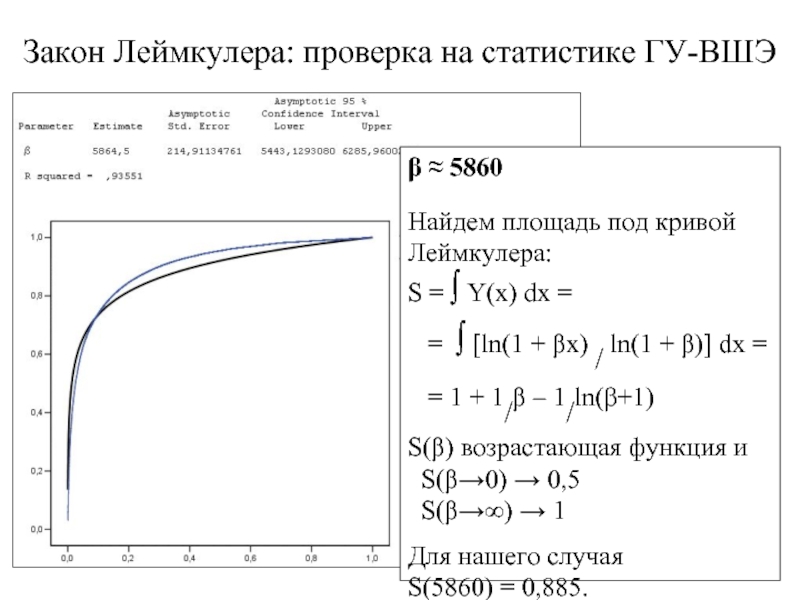
Закон Леймкулера: проверка на статистике ГУ-ВШЭ
нелинейная регрессия
исходные данные
β ≈ 5860
Найдем площадь под кривой Леймкулера:
S = ∫ Y(x) dx =
= ∫ [ln(1 + βx) / ln(1 + β)] dx =
= 1 + 1/β – 1/ln(β+1)
S(β) возрастающая функция и
S(β→0) → 0,5
S(β→∞) → 1
Для нашего случая
S(5860) = 0,885.
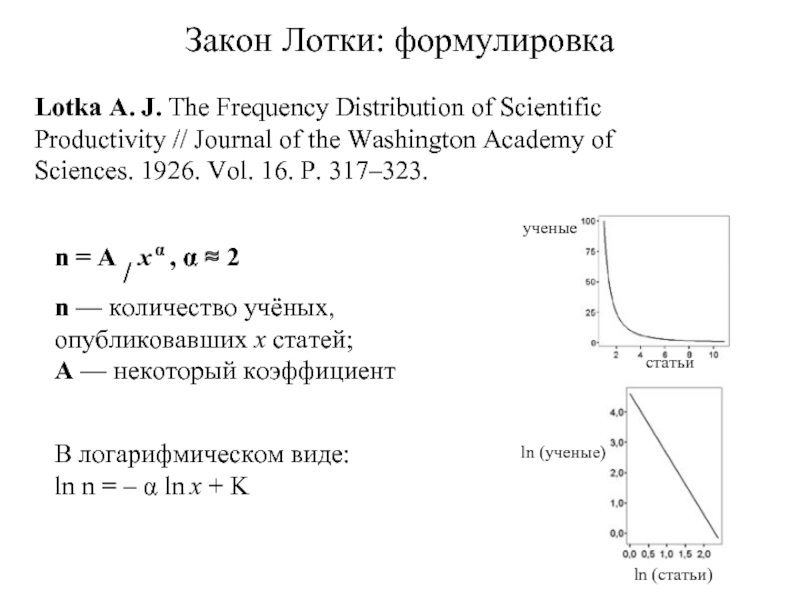
Слайд 12Закон Лотки: формулировка
Lotka A. J. The Frequency Distribution of Scientific Productivity
n = A / x α , α ≈ 2
n — количество учёных, опубликовавших x статей;
A — некоторый коэффициент
В логарифмическом виде:
ln n = – α ln x + K
статьи
ученые
ln (статьи)
ln (ученые)
Слайд 13Приложение закона к статистике использования электронных ресурсов: Найдем, из скольких журналов
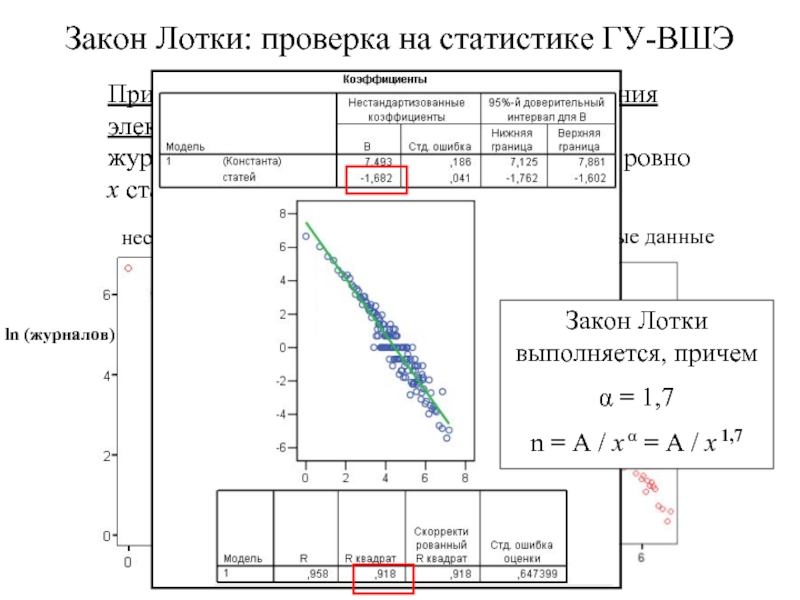
Закон Лотки: проверка на статистике ГУ-ВШЭ
нескорректированные данные
скорректированные данные
ln (журналов)
ln (статей)
Закон Лотки выполняется, причем
α = 1,7
n = A / x α = A / x 1,7
Слайд 14Закон Ципфа: формулировка
Zipf G. K. The Psycho-biology of Language. Boston: Houghton,
Zipf G. K. Human Behaviour and the Principle of Least Effort. Reading: Addison-Wesley, 1949.
r x f = const
r — порядковый номер слова (в порядке убывания частоты);
f — количество употреблений слова
В обобщенном виде:
α ln r + ln f = const, α ≈ 1
(обычно закон Ципфа плохо выполняется для верхних позиций рейтинга слов)
Слайд 15Приложение закона к статистике использования электронных ресурсов: Найдем зависимость между рангом
Закон Ципфа: проверка на статистике ГУ-ВШЭ
Закон Ципфа выполняется удовлетворительно и
α = 1,3
f x r 1,3 = const
ln (статей)
ln (место в рейтинге)
Слайд 16Pareto V. Cours d’Économie Politique. Vol. 2. Lausanne: 1 Université de
Lorenz M. O. Methods of measuring the concentration of wealth // Publications of the American Statisical Association. 1905. Vol. 9. P. 209–219 «Plot along one axis cumulated percents of the population from poorest to richest, and along the other the percent of the total wealth held by these percents» (p. 217)
Gini C. Variabilità e mutabilità // Memori di Metodologia Statistica. Vol. 1. Rome, 1912. P. 211–382.
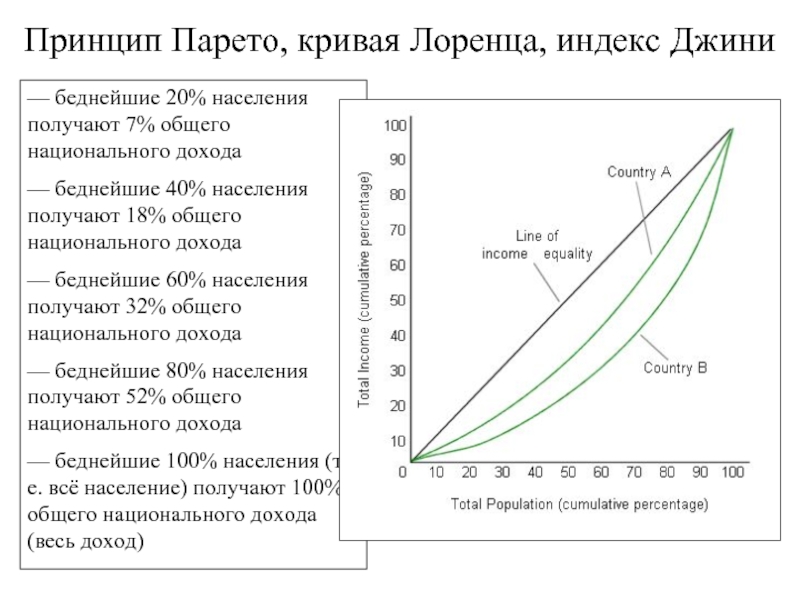
— беднейшие 20% населения получают 7% общего национального дохода
— беднейшие 40% населения получают 18% общего национального дохода
— беднейшие 60% населения получают 32% общего национального дохода
— беднейшие 80% населения получают 52% общего национального дохода
— беднейшие 100% населения (т.е. всё население) получают 100% общего национального дохода (весь доход)
Принцип Парето, кривая Лоренца, индекс Джини
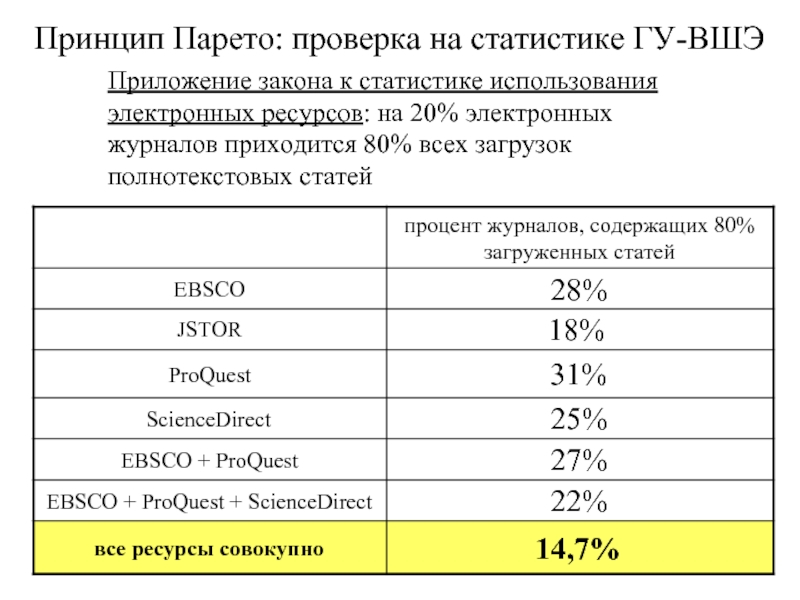
Слайд 18Приложение закона к статистике использования электронных ресурсов: на 20% электронных журналов
Принцип Парето: проверка на статистике ГУ-ВШЭ
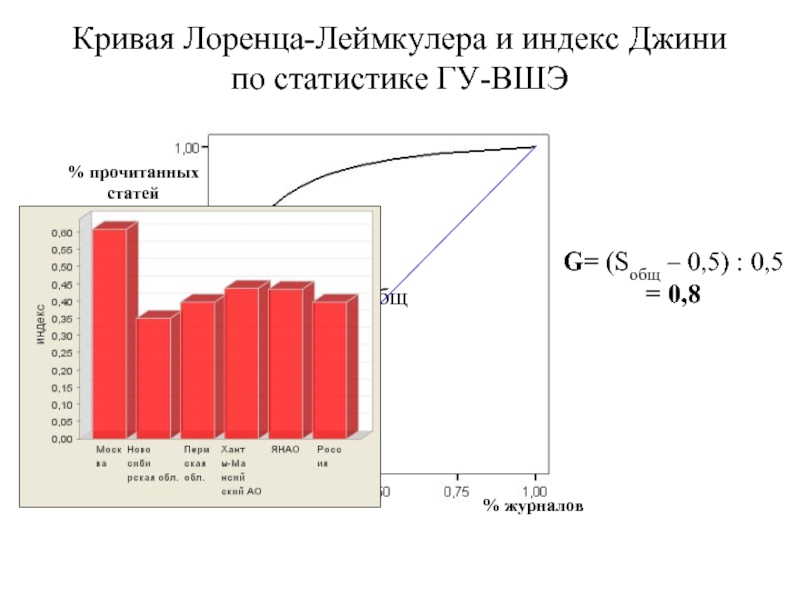
Слайд 19Кривая Лоренца-Леймкулера и индекс Джини
по статистике ГУ-ВШЭ
% журналов
% прочитанных
статей
Sобщ
Sобщ = 0,902
G=
Слайд 20Bookstein A. Informetric Distributions, part I: Unified Overview // Journal of
Garfield E. Bradford’s Law and Realted Statistical Patterns // Current Contents. 1980. No. 19, 12 May.
Egghe L. Type/Token-Taken Informetrics // Journal of the American Society for Information Science and Technology. 2003. Vol. 54. P. 603–610.
Egghe L., Rousseau R. A proposal to define a core of a scientific subject: A definition using concentration and fuzzy sets // Scientometrics. 2002. Vol. 54. No. 1. P. 51–62.
Burrell Q. Defining a core: Theoretical observations on the Egghe-Rousseau proposal // Scientometrics. 2003. Vol. 57. No. 1. P. 75–92.
Библиография
Слайд 21РАСПРЕДЕЛЕНИЕ БРЭДФОРДА И ПОДОБНЫЕ ЕМУ ИНФОМЕТРИЧЕСКИЕ ЗАКОНЫ на примере статистики использования электронных ресурсов в университетской
Владимир Владимирович Писляков
нач. отдела информационных систем
и электронных ресурсов библиотеки ГУ-ВШЭ, Москва
http://library.hse.ru
pislyakov@hse.ru
SCIENCE ONLINE: электронные информационные ресурсы для науки и образования
Турция, 2005