- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Пропорция презентация
Содержание
- 1. Пропорция
- 2. «Геометрия владеет двумя сокровищами: одно из них-
- 3. Человек различает окружающие его предметы по форме.
- 4. Отрезок прямой АВ можно разделить на
- 5. Понятие золотого сечения Золотое сечение – это
- 6. Число Фидия
- 7. A B 1 1 C Д E
- 8. Кеплер называл золотую пропорцию продолжающей саму
- 9. История золотого сечения Принято считать, что понятие
- 10. Золотой треугольник Каждый конец пятиугольной звезды представляет
- 11. Пентаграммы- вместилище золотых пропорций EB:KB=BP:BF= Стороны пентаграммы
- 12. Соотношения связанные
- 13. Соотношения связанные
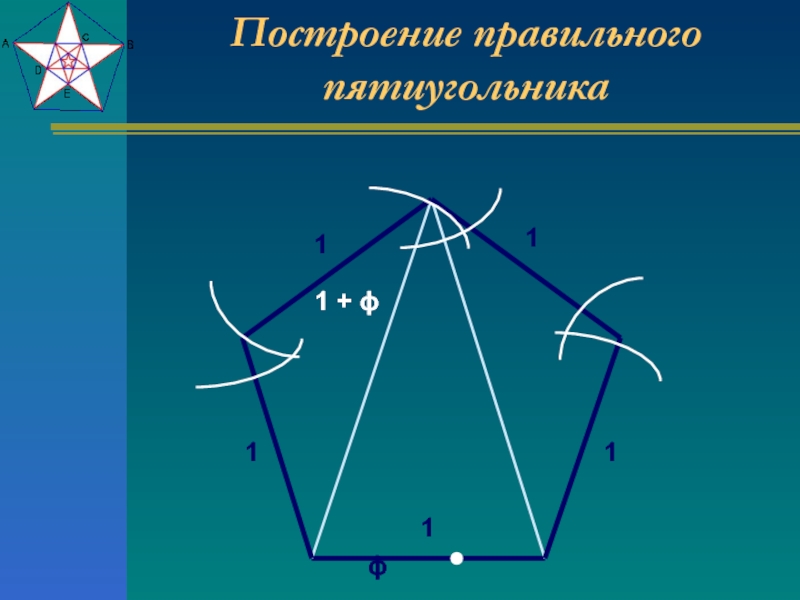
- 14. Построение правильного пятиугольника 1 ϕ 1 + ϕ 1 1 1 1
- 15. Лука Пачоли «О божественной пропорции»
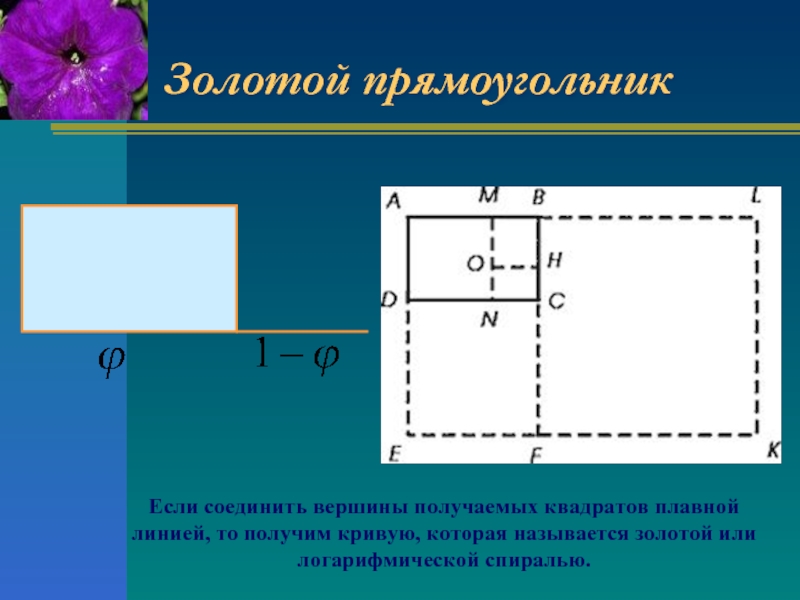
- 16. Золотой прямоугольник Если соединить вершины
- 17. Логарифмическая спираль Логарифмическая спираль единственная из спиралей
- 18. Ряд Фибоначчи С историей золотого сечения косвенным
- 19. Ряд чисел 0, 1, 1, 2, 3,
- 20. Золотое сечение и симметрия Золотое сечение нельзя
- 21. Домашнее задание Задача 1. Построить отрезок длиной
Слайд 2«Геометрия владеет двумя сокровищами: одно из них- теорема Пифагора, другое -
И.Кеплер
Слайд 3Человек различает окружающие его предметы по форме. Интерес к форме какого-либо
«Невозможно, чтобы две вещи совершенным образом соединились без третьей,… это наилучшим образом может выполнить пропорция.»
Тимей
Слайд 4
Отрезок прямой АВ можно разделить на две части следующими способами:
на две
2) на две неравные части в любом отношении (такие части пропорции не образуют);
3) таким образом, когда АВ : АС = АС : ВС.
Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.
Золотое сечение -
гармоничная пропорция
В математике пропорцией называют равенство двух отношений: a : b = c : d. (a*d=b*c)
А
В
С
Слайд 5Понятие золотого сечения
Золотое сечение – это такое пропорциональное деление отрезка на
a : b = b : c или с : b = b : а.
(1-х) : х = х : 1
Слайд 8 Кеплер называл золотую пропорцию продолжающей саму себя. «Устроена она так,
На прямой произвольной длины, отложим отрезок m, рядом откладываем отрезок M. На основании этих двух отрезков выстраиваем шкалу отрезков золотой пропорции восходящего и нисходящего рядов.
Слайд 9История золотого сечения
Принято считать, что понятие о золотом делении ввел в
Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.
Слайд 10Золотой треугольник
Каждый конец пятиугольной звезды представляет собой золотой треугольник. Его стороны
Слайд 11Пентаграммы- вместилище золотых пропорций
EB:KB=BP:BF=
Стороны пентаграммы пересекаясь, делят друг друга на отрезки,
Тр-к KBF подобен тр-ку EBP
Слайд 16Золотой прямоугольник
Если соединить вершины получаемых квадратов плавной линией, то получим кривую,
Слайд 17Логарифмическая спираль
Логарифмическая спираль единственная из спиралей не меняет своей формы при
Слайд 18Ряд Фибоначчи
С историей золотого сечения косвенным образом связано имя итальянского математика
Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами. В 1202 г вышел в свет его математический труд «Книга об абаке» (счетной доске), в котором были собраны все известные на то время задачи. Одна из задач гласила «Сколько пар кроликов в один год от одной пары родится». Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:
Слайд 19Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21,
Свойство чисел ряда Фибоначчи
Слайд 20Золотое сечение и симметрия
Золотое сечение нельзя рассматривать само по себе, отдельно,
Золотое деление не есть проявление асимметрии, чего-то противоположного симметрии. Согласно современным представлениям золотое деление – это асимметричная симметрия.
Слайд 21Домашнее задание
Задача 1. Построить отрезок длиной Ф, если дан квадрат со
Задача 2. С помощью циркуля и линейки построить прямоугольник с отношением сторон 1 : ϕ.
Задача 3. Докажите, что диагональ правильного пятиугольника равна Ф, если сторона этого пятиугольника равна 1.