- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация по геометрии презентация
Содержание
- 1. Презентация по геометрии
- 2. Системы координат Система координат — комплекс определений,
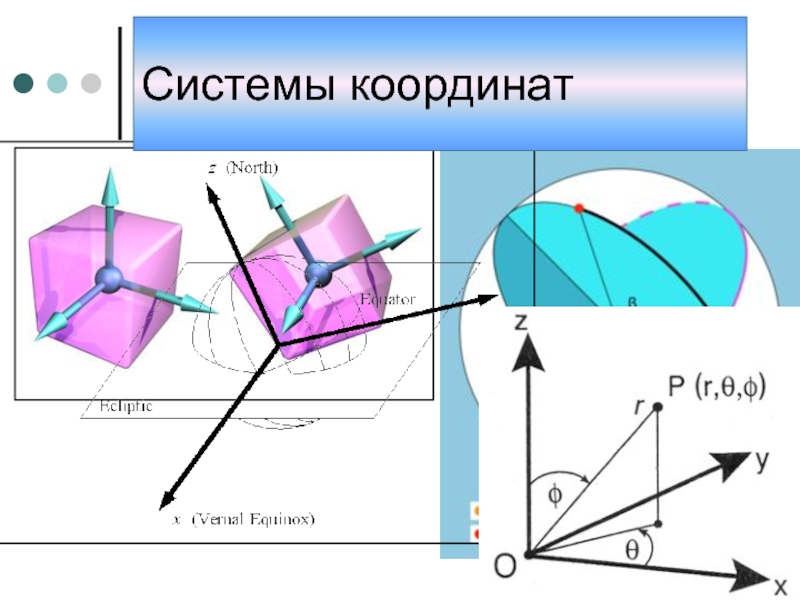
- 3. Различные примеры систем координат Системы координат
- 4. Прямоугольная (Декартова) система координат Аффинная (косоугольная) система
- 5. Прямоугольная (Декартова) система координат Системы координат
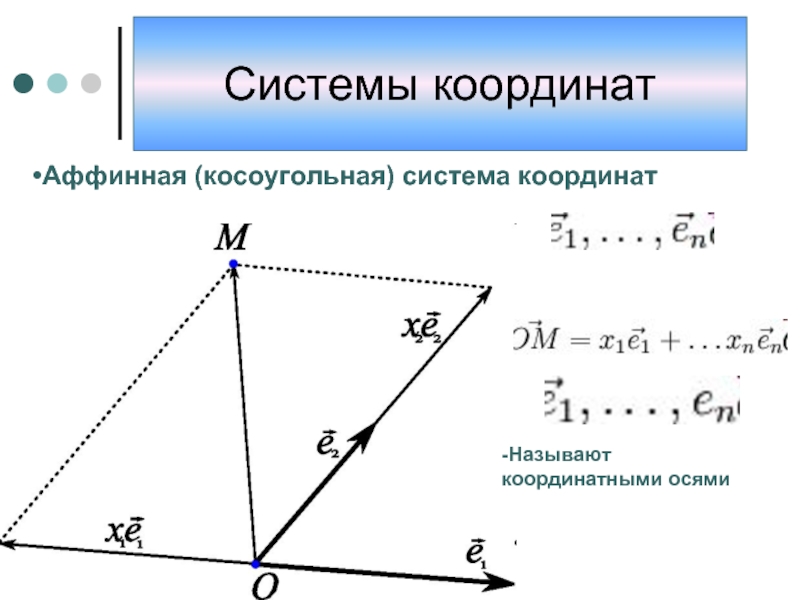
- 6. Аффинная (косоугольная) система координат -Называют координатными осями Системы координат
- 7. Координаты Риндлера Связь с декартовыми координатами Для
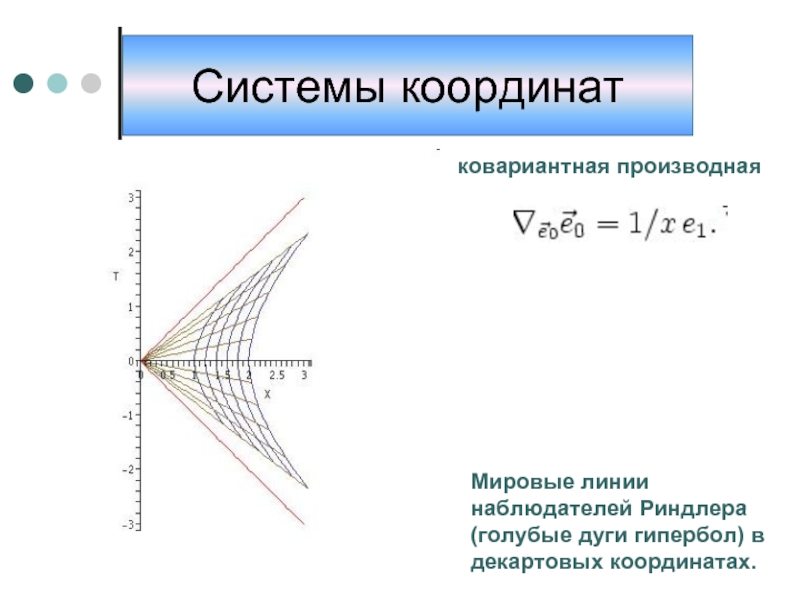
- 8. Мировые линии наблюдателей Риндлера (голубые дуги гипербол) в декартовых координатах. ковариантная производная Системы координат
- 9. Полярная система координат Формулы перехода от
- 10. Примеры использования Уравнение прямой на расстоянии
- 11. Цилиндрическая система координат Точка в цилиндрических координатах 2 точки в цилиндрических координатах Системы координат
- 12. Сферическая система координат Три координаты: (ρ, φ,
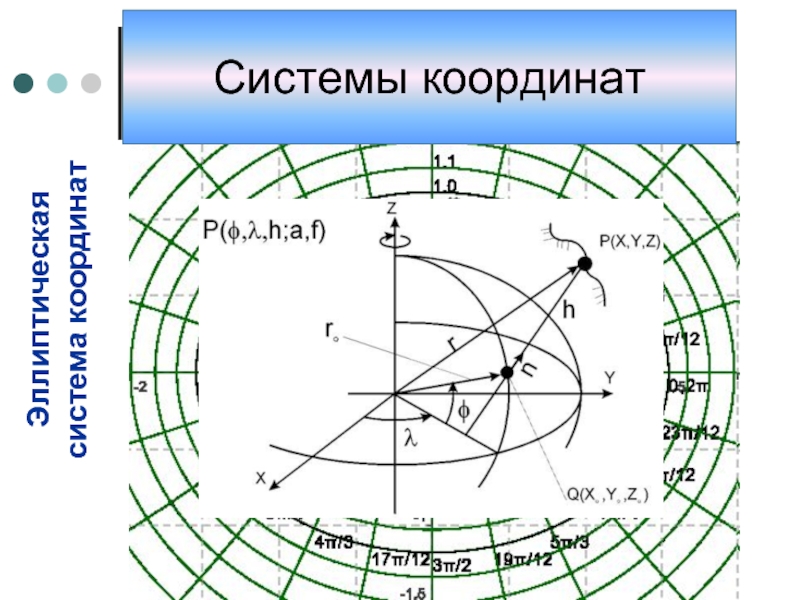
- 13. Эллиптическая система координат Системы координат
- 14. Спасибо за внимание!
Слайд 2Системы координат
Система координат — комплекс определений, реализующий метод координат, то есть
В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.
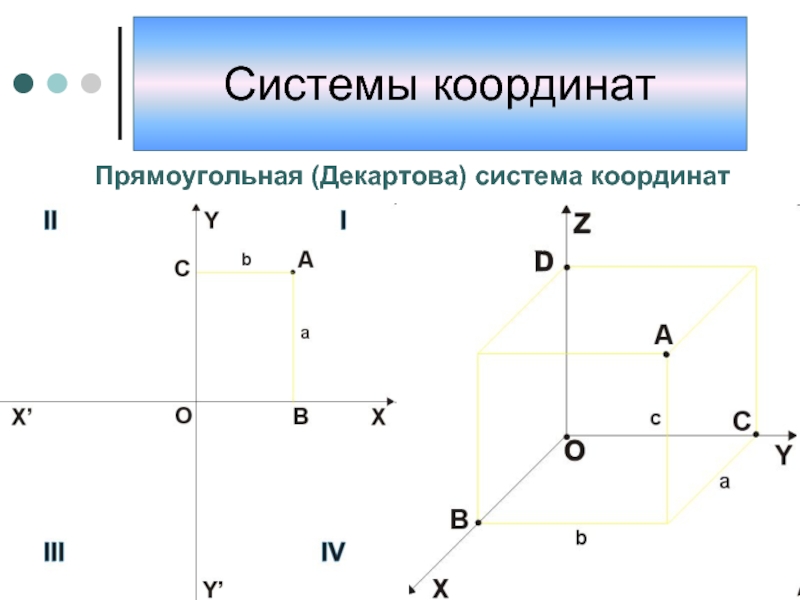
Слайд 4Прямоугольная (Декартова) система координат
Аффинная (косоугольная) система координат
Координаты Риндлера — в пространстве
Барицентрические координаты
Биангулярные координаты
Полярная система координат
Цилиндрическая система координат
Сферическая система координат
Тороидальная система координат
Параболическая система координат
Параболоидальные координаты
Бицентрические координаты
Биполярные координаты
Бицилиндрические координаты
Биангулярные координаты
Трилинейные координаты
Проективные координаты
Эллипсоидальные координаты (эллиптические координаты)
Конические координаты
Системы координат
Слайд 7Координаты Риндлера
Связь с декартовыми координатами
Для получения координат Риндлера естественно начать с
В области , которая часто называется Клином Риндлера, определим новые координаты, через следующее преобразование
Обратным преобразованием будет
В координатах Риндлера линейный элемент пространства Минковского переходит в
Системы координат
Слайд 8Мировые линии наблюдателей Риндлера (голубые дуги гипербол) в декартовых координатах.
ковариантная
Системы координат
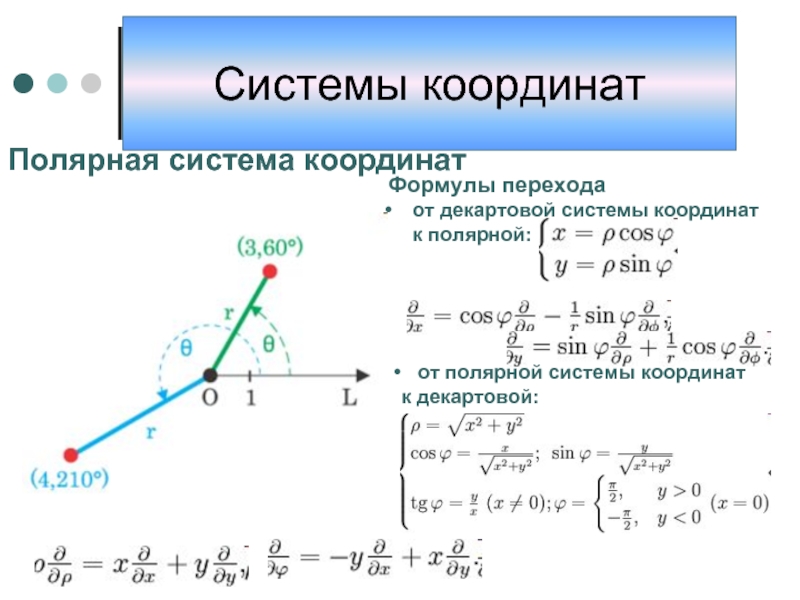
Слайд 9Полярная система координат
Формулы перехода
от декартовой системы координат к полярной:
к декартовой:
Системы координат
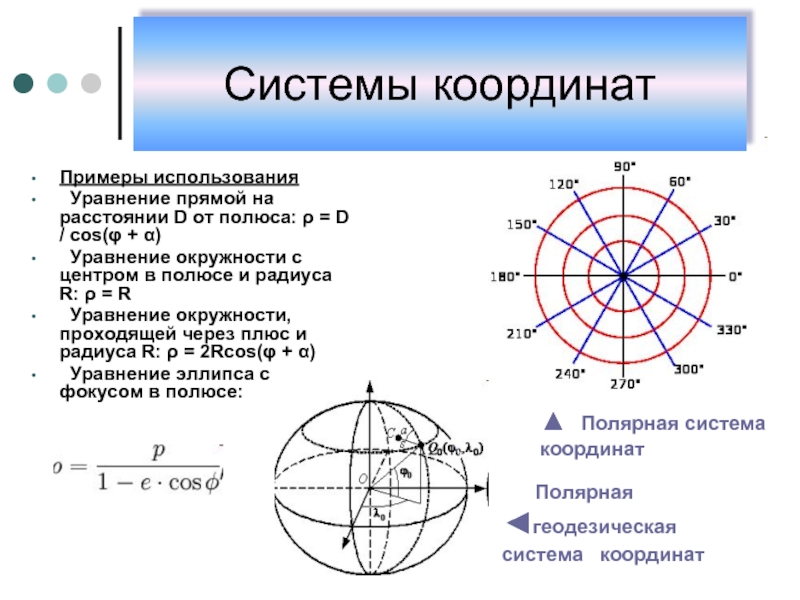
Слайд 10Примеры использования
Уравнение прямой на расстоянии D от полюса: ρ =
Уравнение окружности с центром в полюсе и радиуса R: ρ = R
Уравнение окружности, проходящей через плюс и радиуса R: ρ = 2Rcos(φ + α)
Уравнение эллипса с фокусом в полюсе:
Системы координат
▲ Полярная система координат
Полярная ◄геодезическая система координат
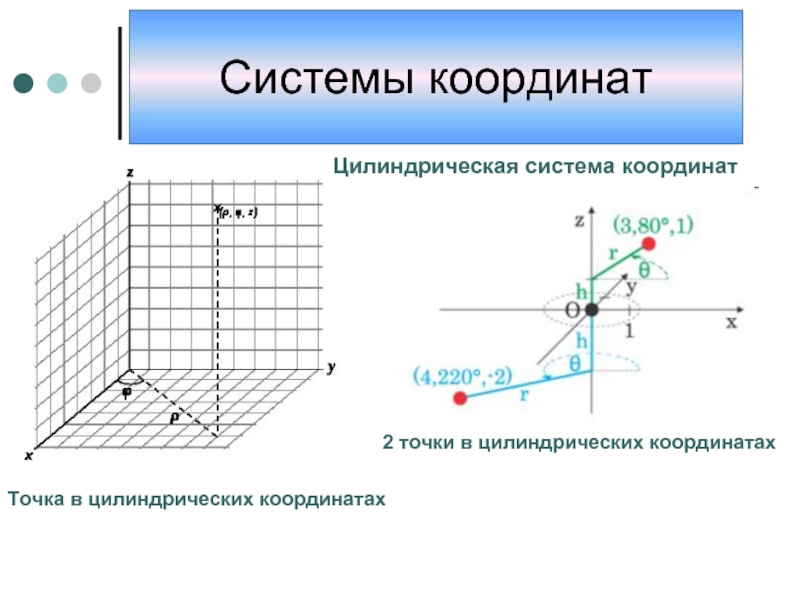
Слайд 11Цилиндрическая система координат
Точка в цилиндрических координатах
2 точки в цилиндрических координатах
Системы координат
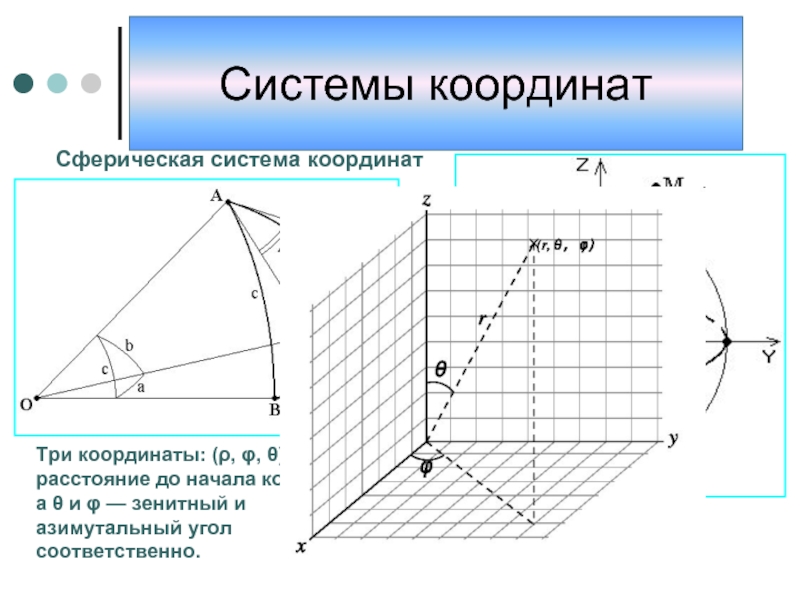
Слайд 12Сферическая система координат
Три координаты: (ρ, φ, θ), где ρ — расстояние
Системы координат