В.В. Абрамов
Институт физики высоких энергий, Протвино, Россия
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Прецессия спина кварка в цветовом поле и поляризация гиперонов в столкновениях тяжёлых ионов презентация
Содержание
- 1. Прецессия спина кварка в цветовом поле и поляризация гиперонов в столкновениях тяжёлых ионов
- 2. План доклада Введение Механизм односпиновых
- 3. Введение Спин является фундаментальной квантовой характеристикой частиц
- 4. Взаимодействие кварка с полем КХД-струны Зависимость
- 5. Действие сил Штерна-Герлаха на кварк в поле
- 6. Прецессия спина кварка в хромомагнитном поле струн
- 7. Поляризационные эффекты в поле КХД струн AN
- 8. Микроскопический эффект Штерна-Герлаха в поле КХД струн
- 9. Глобальная поляризация Λ-гиперонов в соударениях Au+Au (коллайдер
- 10. Глобальная поляризация Λ-гиперонов в соударениях Au+Au Au+Au→Λ:
- 11. Глобальная поляризация Λ̃ –гиперонов в соударениях
- 12. Глобальная поляризация Λ̃ –гиперонов в соударениях
- 13. Поляризация Λ в соударениях Au+Au при энергии
- 14. Правила кваркового счета для ωA ωq
- 15. Зависимость частоты ωA от энергии и атомного
- 16. Объем VT трубки радиуса RT в ядре
- 17. Зависимость частоты ωA от атомного веса сталкивающихся
- 18. Quark counting rules for ωA –
- 19. Quark counting rules for ωA –
- 20. Quark counting rules for ωA –
- 21. Сравнение измеренных значений ωA и предсказаний
- 22. Сравнение измеренных значений ωA и предсказаний
- 23. Заключение Предсказывается осцилляция PN и AN
- 24. Заключение Наблюдается микроскопический эффект Штерна-Герлаха в
- 25. Polarization effects in the string field
- 26. Physical meaning of E0 and preliminary
Слайд 1Прецессия спина кварка в цветовом поле и поляризация гиперонов в столкновениях
Слайд 2План доклада
Введение
Механизм односпиновых эффектов
Данные для Аu+Аu-соударений
Сравнение данных и
Заключение
Слайд 3Введение
Спин является фундаментальной квантовой характеристикой частиц и мощным инструментом для их
A↑ + B → C + X (односпиновая асимметрия, AN(pT, xF,√s) ).
A + B → C↑ + X (поляризация частицы C, PN(pT, xF,√s) ).
В т.в. КХД односпиновые эффекты малы: AN ≈ αSmQ/EQ ≤ 1%.
αS ≈ 0.2 – 0.5; токовая масса mQ ≈ 5-10 МэВ; EQ ≈ PT ≈ 1 ГэВ/с.
Предлагается новый квазиклассический механизм для односпиновых процессов, который основан на взаимодействии массивных составляющих кварков с эффективным хромомагнитным полем глюонных струн. Прецессия спина кварка в цветовом поле приводит к осцилляции поляризации адронов в зависимости от кинематических переменных.
14.46
Слайд 4Взаимодействие кварка с полем КХД-струны
Зависимость поля от расстояния r от
E(3)Z = -2αsν /ρ2 exp(-r2/ρ2), (1)
B(2)φ = -2αsν r/ρ3 exp(-r2/ρ2), (2)
где ν – число кварков, ρ =1.25RC ≈ 2.08 ГэВ-1,
RC-1 ≈ 0.6 ГэВ, RC – радиус конфайнмента, αs = qs2/4π ≈ 0.5;
Продольное хромоэлектрическое Ea и циркулярное хромомагнитное Ba поля КХД-струны.
μ = sgqs/2MQ – хромомагнитный момент составляющего кварка.
JETP Lett. 41, 194 (1985).
14.46
Слайд 5Действие сил Штерна-Герлаха на кварк в поле КХД струны
Эффективное хромомагнитное
Односпиновые эффекты – результат действия сил типа Штерна-Герлаха: (М.Рыскин, ЯФ 48(1988)1114.)
Взаимодействие с электромагнитным полем: M.Conte et al., ICFA Beam Dyn.Newslett. 24,66(2001). Аналогично, для взаимодействия с цветомагнитным полем КХД струн Ba полагаем:
fx ≈ μx ∂Bx/∂x + μy ∂By/∂x (3)
fy ≈ μx ∂Bx/∂y + μy ∂By/∂y (4)
СПЕКТАТОРЫ
14.46
Слайд 6Прецессия спина кварка в хромомагнитном поле струн
Ларморова прецессия спина кварка ξ
dξ/dt ≈ a[ξ B] (BMT-уравнение) (4)
a = qs/2MQ(g – 2 + 2MQ/EQ) (MU ≈ MD ≈ 0.3 ГэВ) (5)
ξy(S) = ξy0 [cos(kS)(Bx/B)2 + (By/B)2], (6)
S – пройденный кварком путь, k = aB/v, dS = vdt, v ≈ c =1.
μa =(g-2)/2 (аномальный хромомагнитный момент кварка)
Инстантонная модель: μa ≈ –0.2 (Кочелев); μa ≈ –0.74 (Дьяконов)
КЭД: μ a ≈ +α /2π ; т.в. КХД: μ a ≈ – αS /6π .
14.46
Слайд 7Поляризационные эффекты в поле КХД струн
AN ≈ δPx ∂/∂pT ln(d3σ/d3p);
AN ≈ C(√s)V(Ecm)F(PT,A)[G(yAωA) – σ(θcm)G(yBωB) ]; (11)
G(X) = [1 – cos(φ)]/φ; - прецессия спина и силы Ш-Г. (12)
yA = xA – (E0/√s + fA )[1 + cos(θcm )] + a0[1 – cos(θcm )] (13)
xA = (xR + xF)/2 – скейлинговая переменная 1
yB = xB – (E0/√s + fB )[1 – cos(θcm )] + a0[1 + cos(θcm )] (14)
xB = (xR – xF)/2 – скейлинговая переменная 2
δPx ≈ gv[1-cos(kS)]/{2ρkS( g - 2 +2MQ /EQ )}, (8)
где k = aB/v, a = qs/2MQ(g – 2 + 2MQ/EQ).
Угол вращения спина: φ = kS = ωAxA ≡ ωA(xR +xF)/2 (9)
14.47
Слайд 8Микроскопический эффект Штерна-Герлаха в поле КХД струн
Эффективное поле КХД-струн, возникающее после
Прецессия спина кварков приводит к осцилляции односпиновых наблюдаемых (AN и PN), как функций кинематических переменных (xF, pT, η,…).
14.47
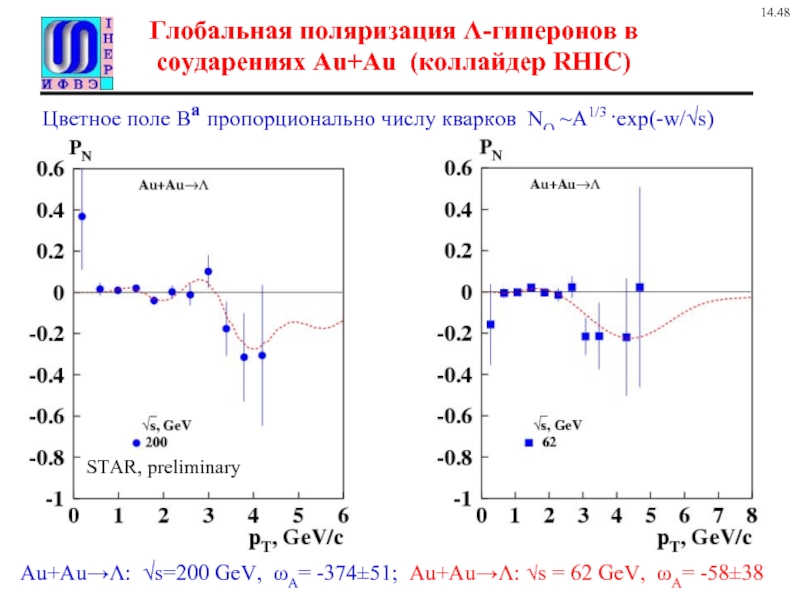
Слайд 9Глобальная поляризация Λ-гиперонов в соударениях Au+Au (коллайдер RHIC)
Au+Au→Λ: √s=200 GeV, ωA=
Цветное поле Ba пропорционально числу кварков NQ ~A1/3 ·exp(-w/√s)
STAR, preliminary
14.48
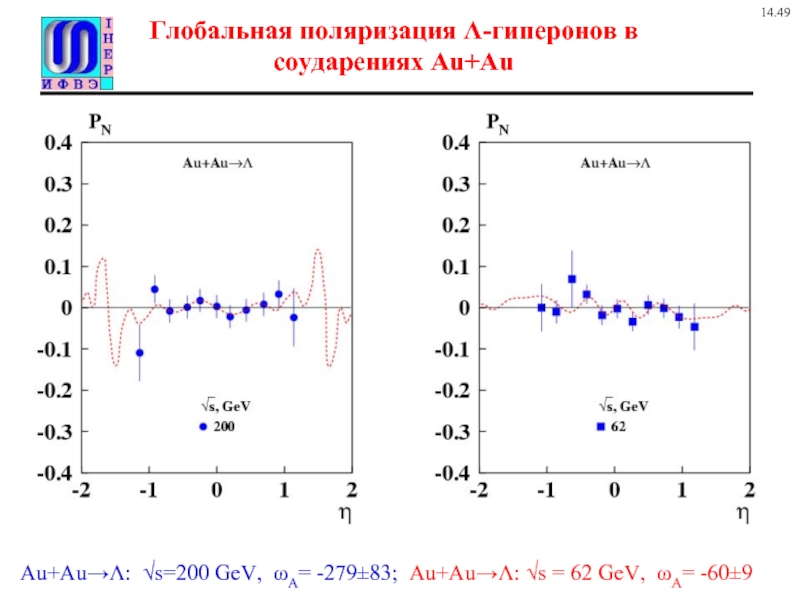
Слайд 10Глобальная поляризация Λ-гиперонов в соударениях Au+Au
Au+Au→Λ: √s=200 GeV, ωA= -279±83; Au+Au→Λ:
14.49
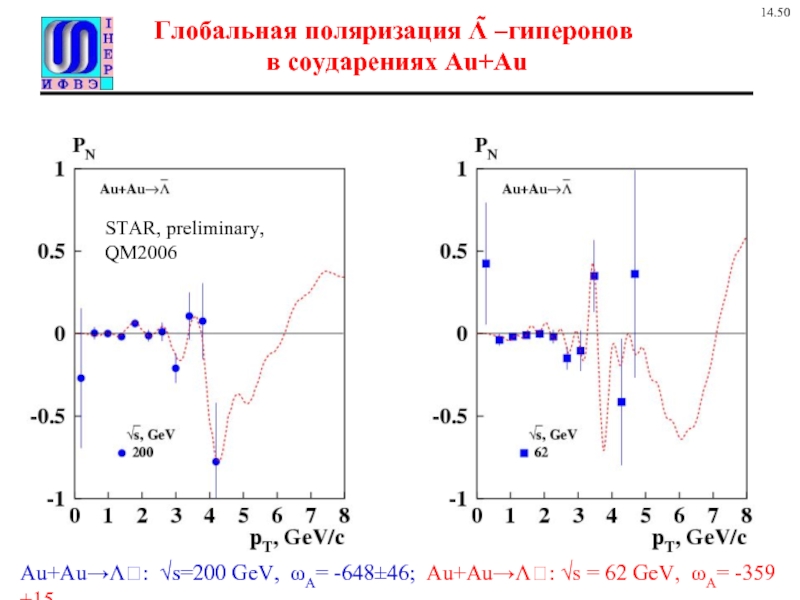
Слайд 11Глобальная поляризация Λ̃ –гиперонов
в соударениях Au+Au
Au+Au→Λ: √s=200 GeV, ωA= -648±46;
STAR, preliminary, QM2006
14.50
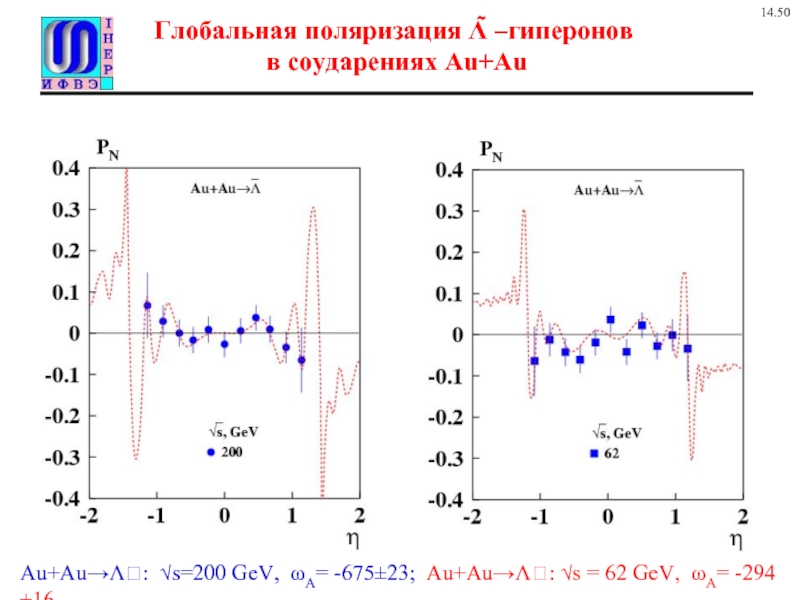
Слайд 12Глобальная поляризация Λ̃ –гиперонов
в соударениях Au+Au
Au+Au→Λ: √s=200 GeV, ωA= -675±23;
14.50
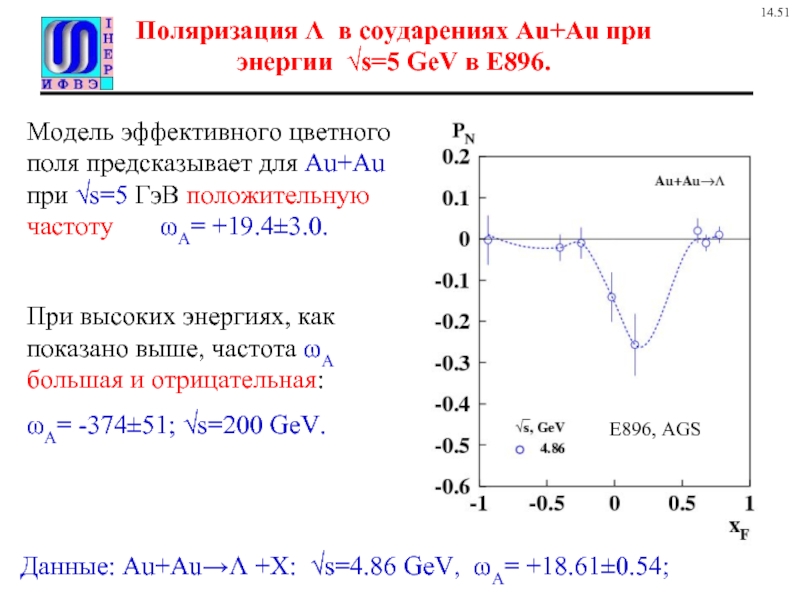
Слайд 13Поляризация Λ в соударениях Au+Au при энергии √s=5 GeV в E896.
Данные: Au+Au→Λ +X: √s=4.86 GeV, ωA= +18.61±0.54;
Модель эффективного цветного поля предсказывает для Au+Au при √s=5 ГэВ положительную частоту ωA= +19.4±3.0.
При высоких энергиях, как показано выше, частота ωA большая и отрицательная:
ωA= -374±51; √s=200 GeV.
E896, AGS
14.51
Слайд 14
Правила кваркового счета для ωA
ωq = ω0 Rq{q̃new +λqnew – q̃used
ωq̃ = ω0 Rq{λq̃new +qnew – λq̃used - qused +qA + λq̃A –τ(qB+ λq̃B)} (16)
Rq=(g-2)qMS/(g-2)SMq; ω0 = –3.24±0.30; λ = –0.106±0.018; τ = –0.016±0.027;
RU=1.60±0.24; RD=1.95±0.41; RS=1; RC=0.78±0.29;
СПЕКТАТОРЫ
Кварки- и антикварки- спектаторы из налетающего адрона вносят аддитивный вклад в ωА, равный λ и 1 соответственно. Спектаторы из мишени имеют дополнительный фактор –τ.
14.52
Слайд 15Зависимость частоты ωA
от энергии и атомного веса ядра
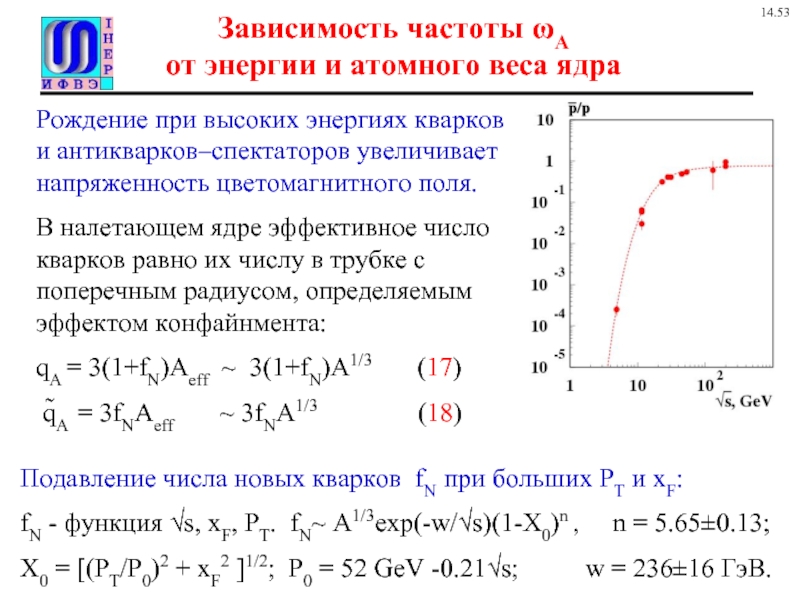
Рождение при высоких энергиях
В налетающем ядре эффективное число кварков равно их числу в трубке с поперечным радиусом, определяемым эффектом конфайнмента:
qA = 3(1+fN)Aeff ~ 3(1+fN)A1/3 (17)
q̃A = 3fNAeff ~ 3fNA1/3 (18)
Подавление числа новых кварков fN при больших PT и xF:
fN - функция √s, xF, PT. fN~ A1/3exp(-w/√s)(1-X0)n , n = 5.65±0.13;
X0 = [(PT/P0)2 + xF2 ]1/2; P0 = 52 GeV -0.21√s; w = 236±16 ГэВ.
14.53
Слайд 16Объем VT трубки радиуса RT в ядре радиуса R:
VT = 4π
где xm = [1 – (RT/R)2]3/2. (77)
Полагая R = r0A1/3, RT = r0Ac1/3, где r0 ≈1.2 Фм, получаем:
Зависимость частоты ωA от атомного веса сталкивающихся ядер
xm = [1 – (Ac/A)2/3]3/2; Aeff = A(1 – xm); (78)
Число кварков в трубке радиуса RT = r0Ac1/3 будет:
3Aeff = 3A(1 – xm) = 3A{1 – [1 – (Ac/A)2/3]3/2} ≈ 11.7A1/3. (79)
Если Ac > A, то Aeff = A. Для нуклонов Aeff = 1.
Ac является свободным параметром модели.
Фит: Ac =4.19 ± 1.13; RT = r0Ac1/3 ≈1.94 ± 0.20 Фм.
14.53
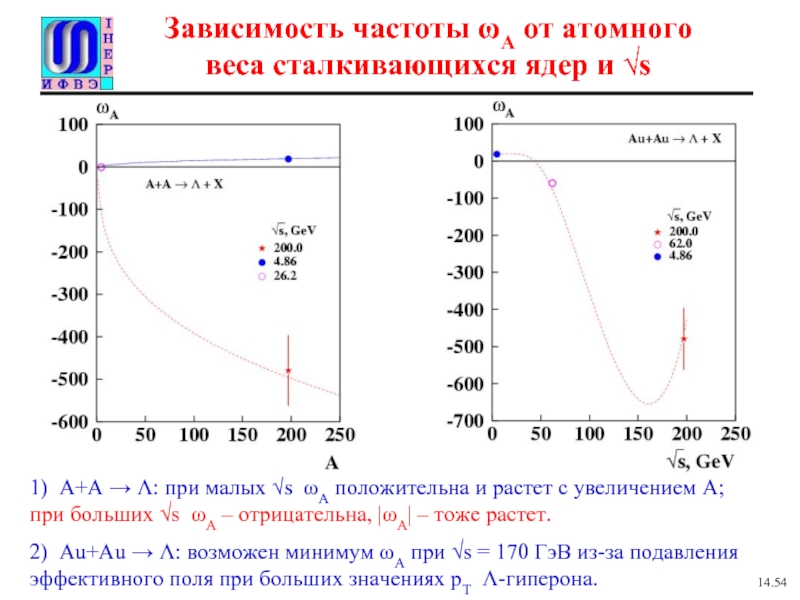
Слайд 17Зависимость частоты ωA от атомного веса сталкивающихся ядер и √s
1) A+A
2) Au+Au → Λ: возможен минимум ωA при √s = 170 ГэВ из-за подавления эффективного поля при больших значениях рТ Λ-гиперона.
14.54
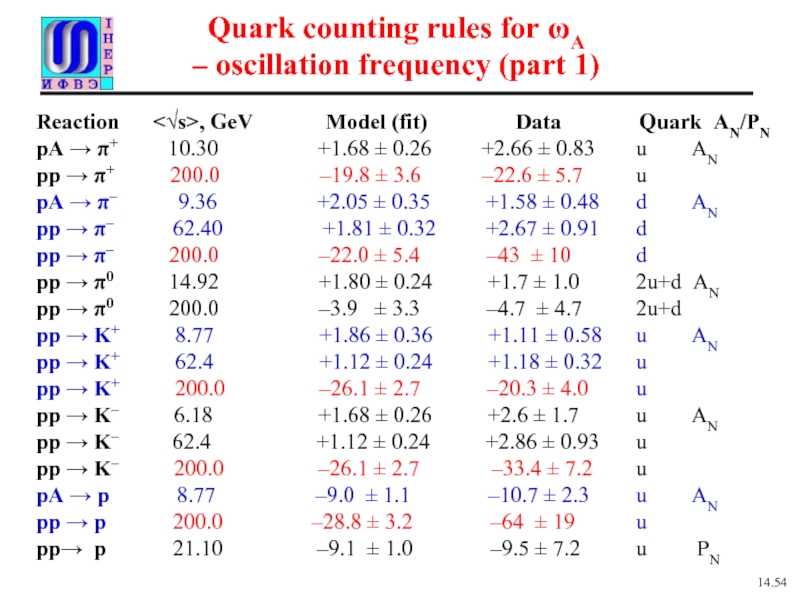
Слайд 18Quark counting rules for ωA
– oscillation frequency (part 1)
Reaction
pA → π+ 10.30 +1.68 ± 0.26 +2.66 ± 0.83 u AN
pp → π+ 200.0 –19.8 ± 3.6 –22.6 ± 5.7 u
pA → π– 9.36 +2.05 ± 0.35 +1.58 ± 0.48 d AN
pp → π– 62.40 +1.81 ± 0.32 +2.67 ± 0.91 d
pp → π– 200.0 –22.0 ± 5.4 –43 ± 10 d
pp → π0 14.92 +1.80 ± 0.24 +1.7 ± 1.0 2u+d AN
pp → π0 200.0 –3.9 ± 3.3 –4.7 ± 4.7 2u+d
pp → K+ 8.77 +1.86 ± 0.36 +1.11 ± 0.58 u AN
pp → K+ 62.4 +1.12 ± 0.24 +1.18 ± 0.32 u
pp → K+ 200.0 –26.1 ± 2.7 –20.3 ± 4.0 u
pp → K– 6.18 +1.68 ± 0.26 +2.6 ± 1.7 u AN
pp → K– 62.4 +1.12 ± 0.24 +2.86 ± 0.93 u
pp → K– 200.0 –26.1 ± 2.7 –33.4 ± 7.2 u
pA → p 8.77 –9.0 ± 1.1 –10.7 ± 2.3 u AN
pp → p 200.0 –28.8 ± 3.2 –64 ± 19 u
pp→ p 21.10 –9.1 ± 1.0 –9.5 ± 7.2 u PN
14.54
Слайд 19Quark counting rules for ωA
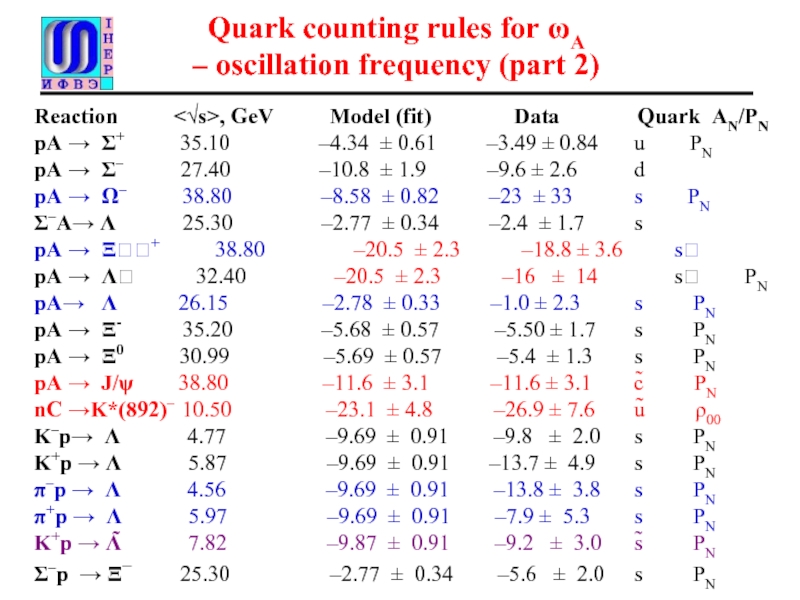
– oscillation frequency (part 2)
Reaction
pA → Σ+ 35.10 –4.34 ± 0.61 –3.49 ± 0.84 u PN
pA → Σ– 27.40 –10.8 ± 1.9 –9.6 ± 2.6 d
pA → Ω– 38.80 –8.58 ± 0.82 –23 ± 33 s PN
Σ–A→ Λ 25.30 –2.77 ± 0.34 –2.4 ± 1.7 s
pA → Ξ+ 38.80 –20.5 ± 2.3 –18.8 ± 3.6 s
pA → Λ 32.40 –20.5 ± 2.3 –16 ± 14 s PN
pA→ Λ 26.15 –2.78 ± 0.33 –1.0 ± 2.3 s PN
pA → Ξ- 35.20 –5.68 ± 0.57 –5.50 ± 1.7 s PN
pA → Ξ0 30.99 –5.69 ± 0.57 –5.4 ± 1.3 s PN
pA → J/ψ 38.80 –11.6 ± 3.1 –11.6 ± 3.1 c̃ PN
nC →K*(892)– 10.50 –23.1 ± 4.8 –26.9 ± 7.6 ũ ρ00
K–p→ Λ 4.77 –9.69 ± 0.91 –9.8 ± 2.0 s PN
K+p → Λ 5.87 –9.69 ± 0.91 –13.7 ± 4.9 s PN
π–p → Λ 4.56 –9.69 ± 0.91 –13.8 ± 3.8 s PN
π+p → Λ 5.97 –9.69 ± 0.91 –7.9 ± 5.3 s PN
K+p → Λ̃ 7.82 –9.87 ± 0.91 –9.2 ± 3.0 s̃ PN
Σ–p → Ξ– 25.30 –2.77 ± 0.34 –5.6 ± 2.0 s PN
Слайд 20Quark counting rules for ωA
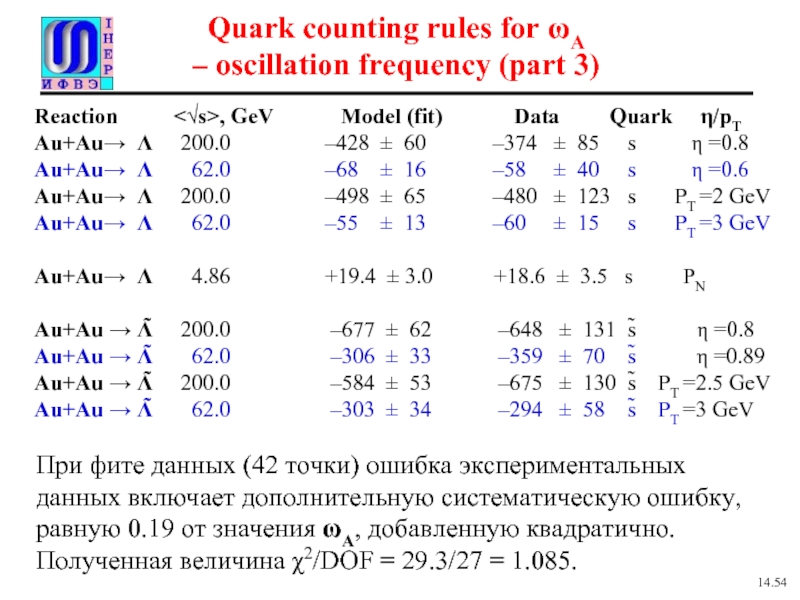
– oscillation frequency (part 3)
Reaction
Au+Au→ Λ 200.0 –428 ± 60 –374 ± 85 s η =0.8
Au+Au→ Λ 62.0 –68 ± 16 –58 ± 40 s η =0.6
Au+Au→ Λ 200.0 –498 ± 65 –480 ± 123 s PT =2 GeV
Au+Au→ Λ 62.0 –55 ± 13 –60 ± 15 s PT =3 GeV
Au+Au→ Λ 4.86 +19.4 ± 3.0 +18.6 ± 3.5 s PN
Au+Au → Λ̃ 200.0 –677 ± 62 –648 ± 131 s̃ η =0.8
Au+Au → Λ̃ 62.0 –306 ± 33 –359 ± 70 s̃ η =0.89
Au+Au → Λ̃ 200.0 –584 ± 53 –675 ± 130 s̃ PT =2.5 GeV
Au+Au → Λ̃ 62.0 –303 ± 34 –294 ± 58 s̃ PT =3 GeV
При фите данных (42 точки) ошибка экспериментальных данных включает дополнительную систематическую ошибку, равную 0.19 от значения ωA, добавленную квадратично. Полученная величина χ2/DOF = 29.3/27 = 1.085.
14.54
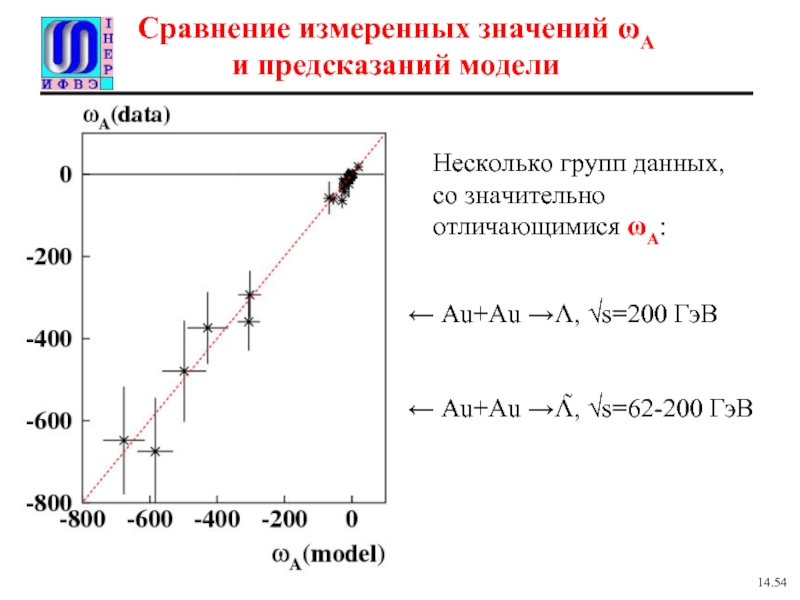
Слайд 21Сравнение измеренных значений ωA
и предсказаний модели
Несколько групп данных, со значительно
← Au+Au →Λ̃, √s=62-200 ГэВ
← Au+Au →Λ, √s=200 ГэВ
14.54
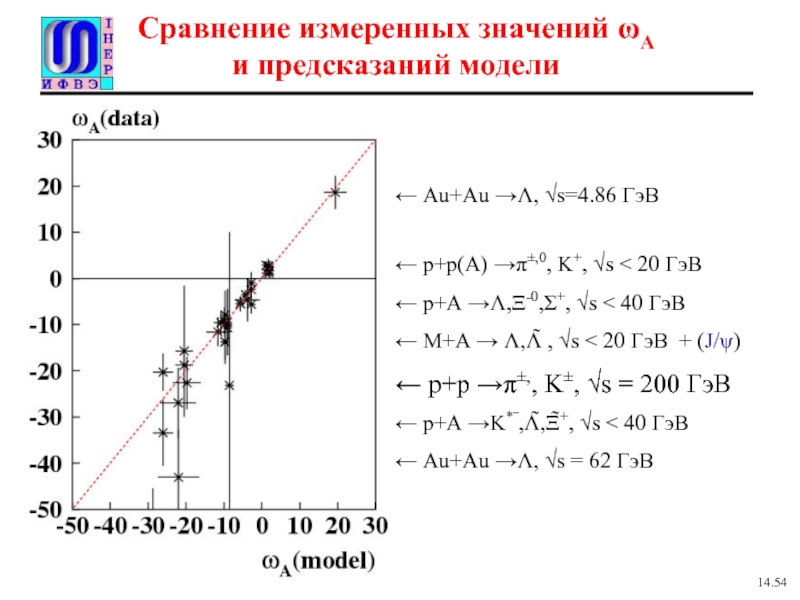
Слайд 22Сравнение измеренных значений ωA
и предсказаний модели
← Au+Au →Λ, √s=4.86 ГэВ
←
← p+A →Λ,Ξ-0,Σ+, √s < 40 ГэВ
← M+A → Λ,Λ̃ , √s < 20 ГэВ + (J/ψ)
← p+p →π±,, K±, √s = 200 ГэВ
← p+A →K*‾,Λ̃,Ξ̃+, √s < 40 ГэВ
← Au+Au →Λ, √s = 62 ГэВ
14.54
Слайд 23Заключение
Предсказывается осцилляция PN и AN как результат прецессии спина составляющего
Осцилляции PN и AN наблюдаются в соударениях тяжелых ионов (Au+Au → Λ (Λ̃)) и в образовании других адронов (р, J/ψ, K*(892)-, Ξ0, Ξ- ) в рр и рА-соударениях.
Частота осцилляции ωA описывается правилами кваркового счета и растет по абсолютной величине при увеличении энергии √s и атомного веса сталкивающихся ядер.
14.55
Слайд 24Заключение
Наблюдается микроскопический эффект Штерна-Герлаха в поле КХД струн
Суперпозиция полей,
The end
14.56
Слайд 25Polarization effects in the string field
AN ≈ C(√s)V(Ecm)F(PT,A)[G(yAωA) – σ(θcm)G(yBωB)
σ(θcm) = χ sin(θcm) + ε; (σ=1 for A ≡B) (15)
C (√s) = C0/(1 – ER/√s ); (2MQ/EQ/(g-2) ~ ER/√s ); (16)
V(Ecm) ≈ ± Θ(Ecm –EcmTh), where Ecm –hadron energy in c.m. (17)
F(PT,A) = {1 – exp[-(PT/d0)3 ]}(1 – η lnA) – PT and A-dependence.
Phenomenological parameters (N=12): ωA, ωB, a0, E0, C0, ER, χ, ε, η, fA, fB, d0. In case of A≡B we have ωA=ωB, fA=fB, χ =0, ε = 1.
Eq. (11) predicts oscillation of AN or PN as a function of scaling variable yA ( yB ) with frequency ωA (ωB) which depends on quantum numbers of hadrons A, B, C, and reaction energy √s. In the case of heavy ion collisions it depends also on a projectile A atomic number.
Слайд 26Physical meaning of E0 and preliminary estimate of (g-2)Q
Model phenomenological
E0 is related with threshold energy in c.m. (where AN or PN =0).
E0 ≈ 2MQ[1 +2/(2 – g)], where MU ≈ MD ≈ 0.35 GeV; (22)
Data fit: E0 = 2.02 ± 0.21 GeV (π–) and E0 = 1.640 ± 0.040 GeV (π+);
μa =(g-2)d /2 ≈ – 0.53 +0.10-0.07 ; μa =(g-2)u /2 ≈ – 0.745 ± 0.033;
These model dependent estimations of μa=(g-2)/2 are in the range of the existing instanton model predictions:
μa = -0.2 (N.Kochelev) and μa = -0.74 (D.Diakonov)












![Polarization effects in the string field AN ≈ C(√s)V(Ecm)F(PT,A)[G(yAωA) – σ(θcm)G(yBωB) ]; (11)](/img/tmb/2/189654/c2f1f30634b1699ed0b325f196f775eb-800x.jpg)






