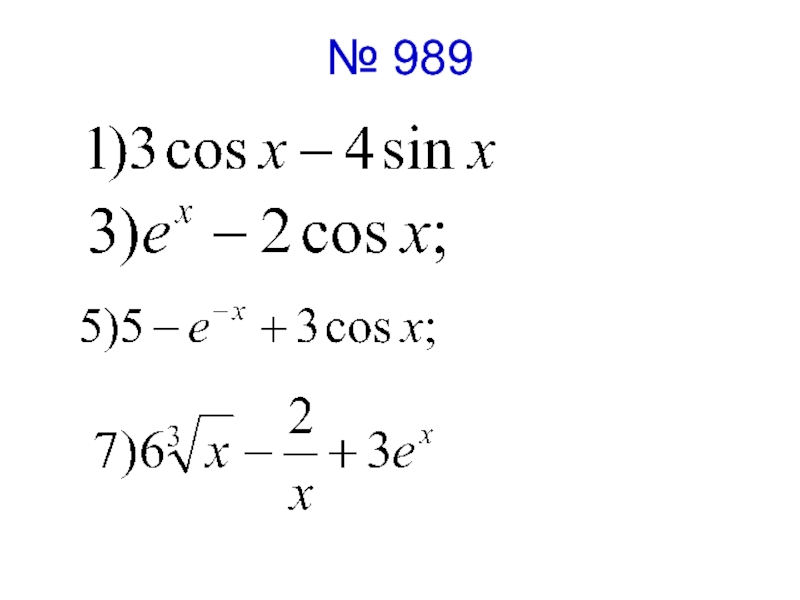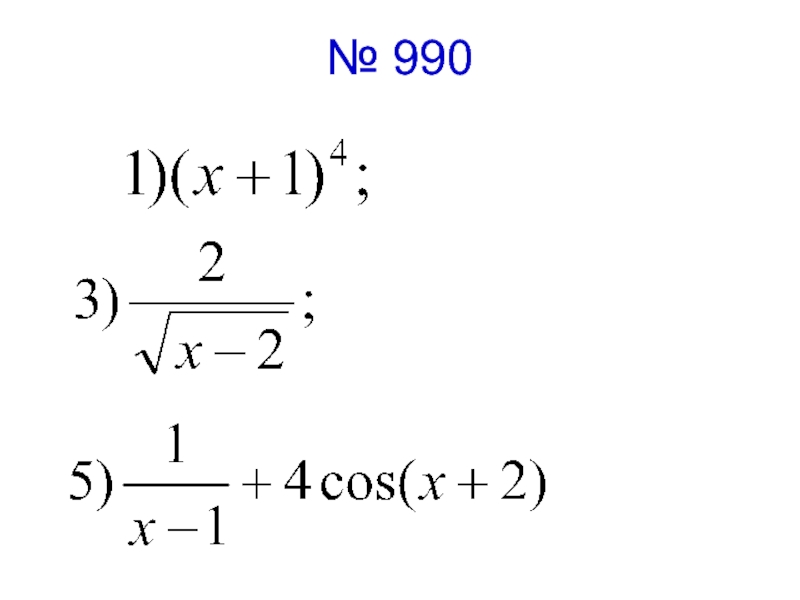Правила нахождения первообразной. презентация

Содержание

1. Правила нахождения первообразной.
2. Устно: Найдите производную функции
3. Задача о движении точки Точка движется с
4. Задача о движении точки Точка движется
5. Функция F(х) называется первообразной функции f(х)
6. Если функция F(х) является первообразной функции f(х)
7. Пусть F(x) и G(x) –первообразные соответственно функций
8. В классе: № 989(1,3,5,7) № 990(1,3,5) № 991 № 994
9. № 989
10. № 990
12. №991 1)sin(2x+3); 2) cos (3x+4);
14. Дома: № 989(2,4,6,8) № 990(2,4)

Главная
Разное
Правила нахождения первообразной.

Слайд 1Правила нахождения первообразной.

Слайд 2Устно: Найдите производную функции

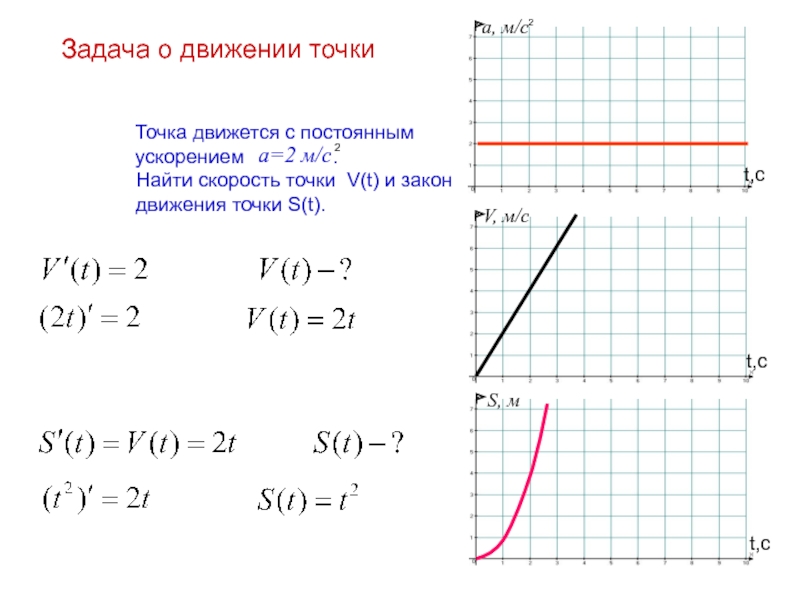
Слайд 3Задача о движении точки
Точка движется с постоянным
ускорением

Найти скорость точки V(t) и закон
движения точки S(t).

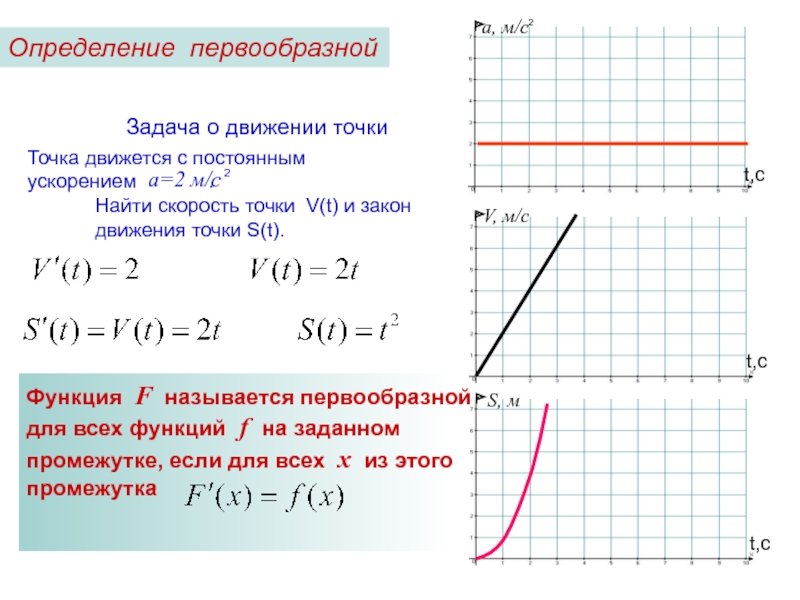
Слайд 4
Задача о движении точки
Точка движется с постоянным ускорением

Найти скорость точки V(t) и закон
движения точки S(t).

Функция F называется первообразной
для всех функций f на заданном
промежутке, если для всех х из этого
промежутка

Определение первообразной

Слайд 5Функция F(х) называется первообразной функции f(х) на некотором промежутке, если для

всех х из этого промежутка F'(x) = f(х)

Для заданной функции ее
первообразная определяется неоднозначно

Слайд 6Если функция F(х) является первообразной функции f(х) на некотором промежутке, то все

первообразные функции f(х) записываются в виде F(х) + С, где С - произвольная постоянная

Если функция F(х) одна из
первообразных функции f(х),
то любая первообразная этой функции получается прибавлением к F(х) некоторой постоянной: F(х) + С.

Графики функций у = F(х) + С получаются из графика у = F(х)
сдвигом вдоль оси Оу