- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Потеря устойчивости мостичного амортизатора из эластомера презентация
Содержание
- 1. Потеря устойчивости мостичного амортизатора из эластомера
- 2. Начальное состояние системы Tz – усилие, сжимающее
- 3. Несимметричная деформация
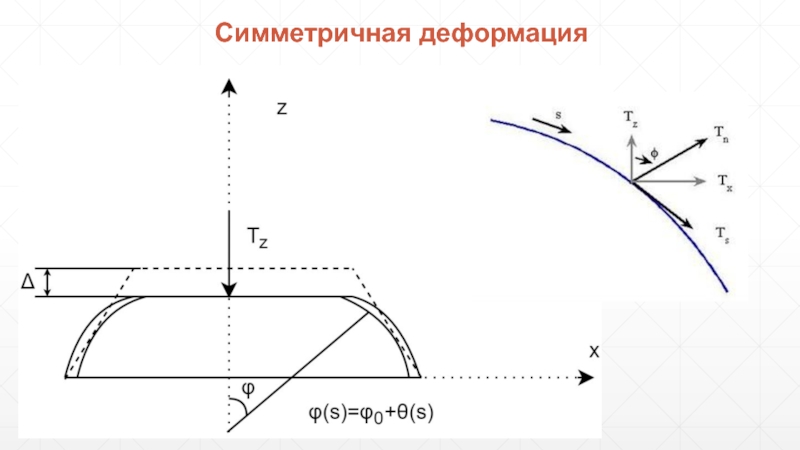
- 4. Симметричная деформация
- 5. λ – кратность удлинения срединной поверхности
- 6. Задача решается методом Стрельбы в сочетании с
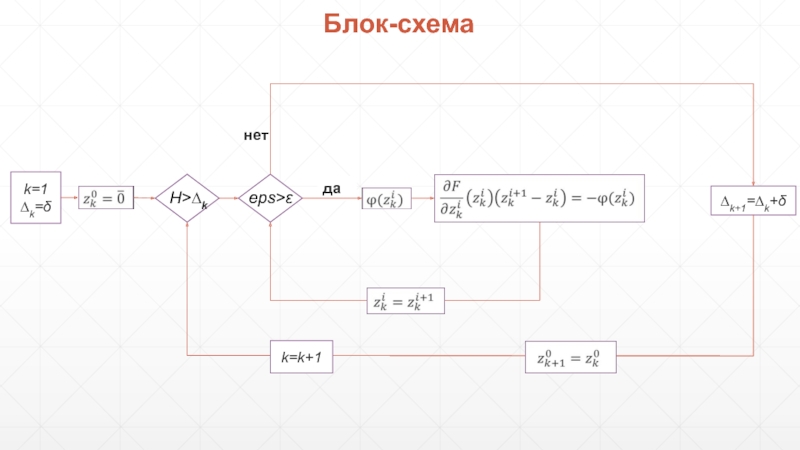
- 7. Блок-схема k=1 ∆k=δ
- 8. Используемая литература Черных К.Ф. Нелинейная
Слайд 1Потеря устойчивости мостичного амортизатора из эластомера
Студент: Горх Э.В.
Научный руководитель: Кабриц С.А.
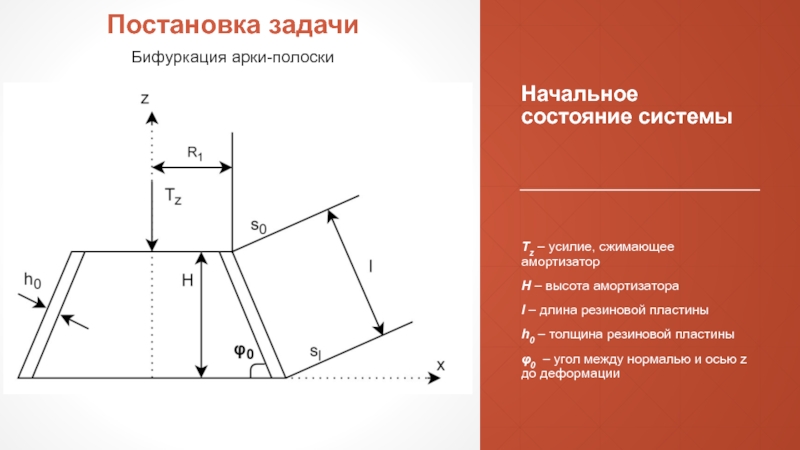
Слайд 2Начальное состояние системы
Tz – усилие, сжимающее амортизатор
H – высота амортизатора
l –
h0 – толщина резиновой пластины
φ0 – угол между нормалью и осью z до деформации
Постановка задачи
Бифуркация арки-полоски
Слайд 5 λ – кратность удлинения срединной поверхности арки-полоски по s κ – изменение
Система уравнений, описывающая деформацию арки-полоски
– блок геометрии
v – перемещение по оси x
u – перемещение по оси z
θ – угол поворота
M – изгибающий момент
Tx – проекция усилия на ось x
Tz – проекция усилия на ось z
Ts – проекция усилия на касательную
Tn – перерезывающее усилие
Слайд 6Задача решается методом Стрельбы в сочетании с методом продолжения по параметру
Здесь:
V
W – переменные λ, κ, Ts , Tn
Слайд 8
Используемая литература
Черных К.Ф. Нелинейная теория изотропно-упругих тонких оболочек. Изв. АН СССР.
Колпак Е.П. О краевом эффекте в нелинейной теории тонких оболочек. Механика эластомеров, №4, 1981. Краснодар, из-во КПИ. Стр. 87-95.
С.А. Кабриц, Е.И. Михайловский, П.Е. Товстик, К.Ф. Черных, В.А. Шамин. Общая нелинейная теория упругих оболочек. 2002. 376 с.
Черных К.Ф. Нелинейная теория упругости (в машиностроительных расчетах). 1986. 336 с.
Пановко Я.Г., Губанова И.И. Устойчивость и колебания упругих систем. С.74.
Бахвалов Н.С. Численные методы (анализ, алгебра, обыкновенные дифференциальные уравнения). 1973. 631 с.
Статьи:
А.Е. Белкин, В.В. Семенов, В.К. Семенов. Численный анализ больших плоский деформаций арочного амортизатора. Вестник МГТУ им. Н.Э. Баумана. 2011
А.Е. Белкин, Д.С. Хоминич. Расчет больших деформаций арочного амортизатора с учетом объемной сжимаемости резины.