- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Построение уточненной теории пластин с применением уравнения равновесия элементарного столбика Выполнил: Скращук Дмитрий Геннадьевич Руководитель: профессор Крушевский Александр Евгеньевич презентация
Содержание
- 1. Построение уточненной теории пластин с применением уравнения равновесия элементарного столбика Выполнил: Скращук Дмитрий Геннадьевич Руководитель: профессор Крушевский Александр Евгеньевич
- 2. Элементарный столбик Постановка задачи Решение задачи Результаты Выводы
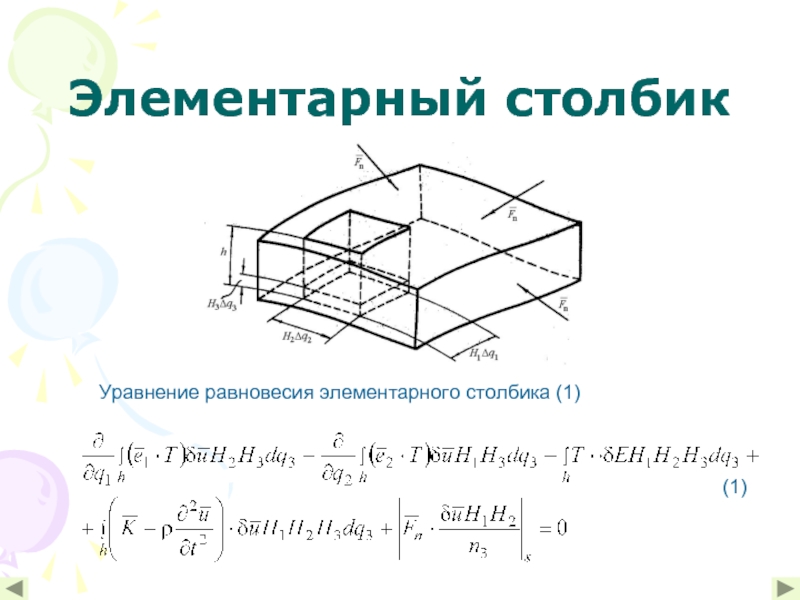
- 3. Элементарный столбик Уравнение равновесия элементарного столбика (1) (1)
- 4. Постановка задачи Дана круглая толстая плита
- 5. Решение задачи Для решения поставленной
- 6. Решение задачи Раскрывая вариационное уравнение
- 7. Решение задачи Их общие решения приведенные принимают
- 8. Решение задачи Применяя метод неопределённых коэффициентов можно
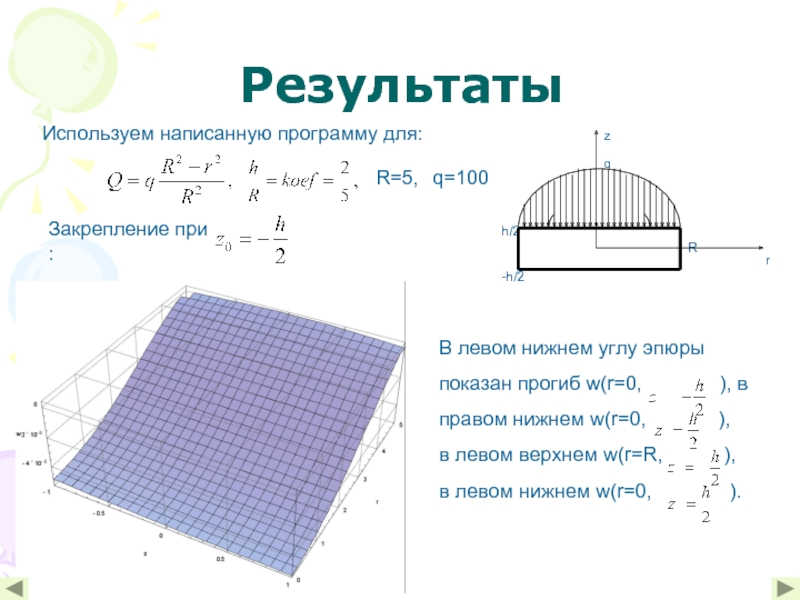
- 9. Результаты R=5, q=100 Используем
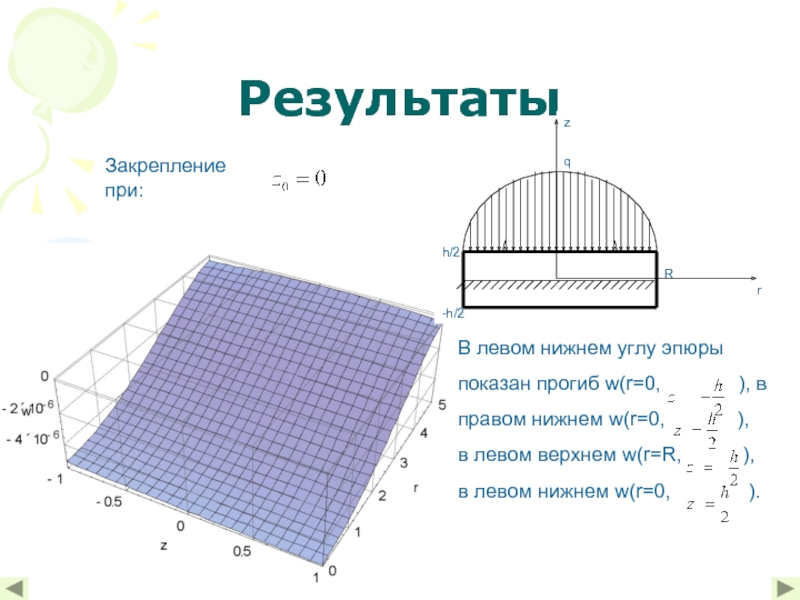
- 10. Результаты Закрепление при: :
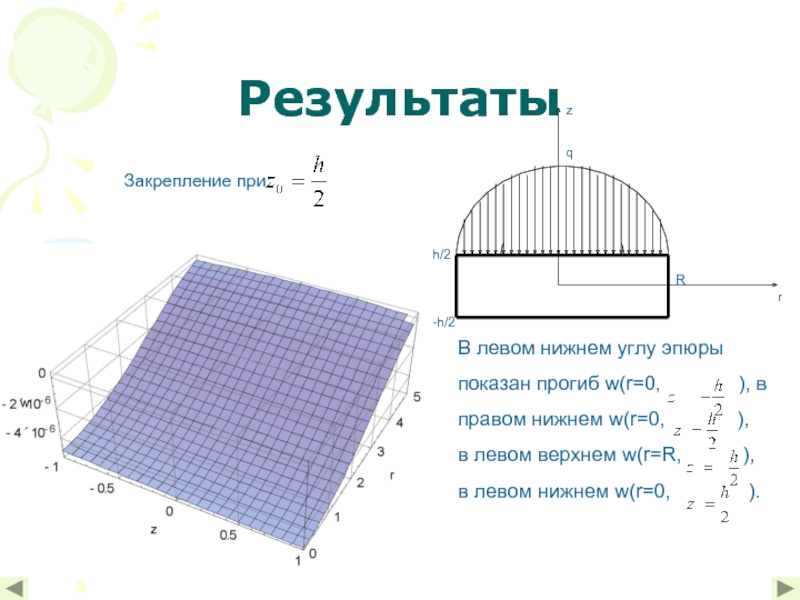
- 11. Результаты Закрепление при:
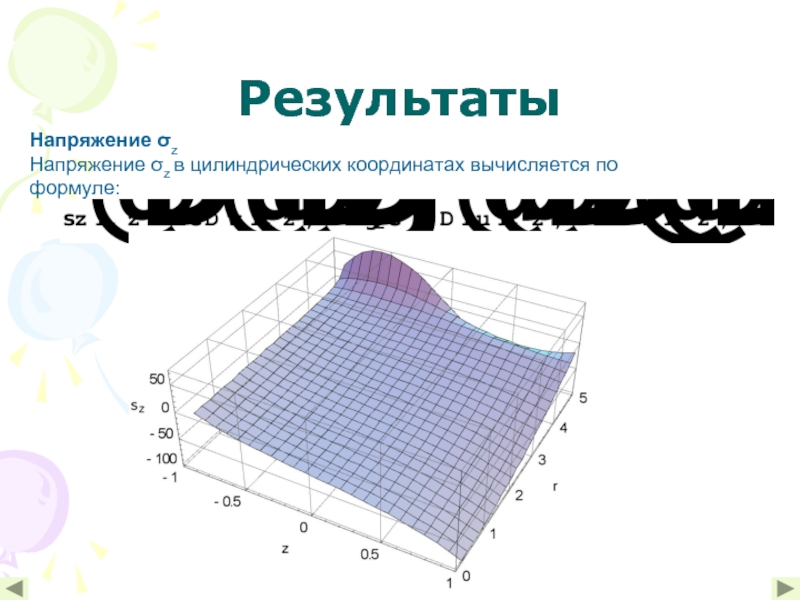
- 12. Результаты Напряжение σz Напряжение σz в цилиндрических координатах вычисляется по формуле:
- 13. Результаты Напряжение τrz в цилиндрических координатах вычисляется
- 14. Выводы Основными новыми результатами работы являются:
- 15. Спасибо за внимание
Слайд 1Построение уточненной теории пластин с применением уравнения равновесия элементарного столбика Выполнил:
Слайд 4Постановка задачи
Дана круглая толстая плита нагруженная параболической нагрузкой, края которой
Используя уравнение равновесия элементарного столбика исследовать:
Зависимость вертикальных перемещений w круглой толстой плиты от положения контура закрепления.
2. Зависимость напряжений σz и τrz круглой толстой от положения контура закрепления.
Слайд 5 Решение задачи
Для решения поставленной задачи используем уравнение равновесия элементарного
,
(2)
(3)
Слайд 6 Решение задачи
Раскрывая вариационное уравнение (1) для разложений (2) и
Слайд 8Решение задачи
Применяя метод неопределённых коэффициентов можно построить решения для Wi и
Ui найдём из следующих условий:
Слайд 13Результаты
Напряжение τrz в цилиндрических координатах вычисляется по формуле:
τrz [r, z]=G( D[u[r,
Напряжение τrz:
Слайд 14Выводы
Основными новыми результатами работы являются:
1. Разработана программа для нахождения вертикального
края которой находятся в абсолютно жёстких вертикальных направляющих, препятствующих тангенциальному перемещению, причём контурная окружность неподвижна.
2. Проведено численное исследование напряжённо-деформированного состояния круглой пластины нагруженной параболической нагрузкой.
3. Вычислены прогибы пластины во всех точках, а также напряжения σz и τrz.
4. Обнаружено, что напряжения σz и τrz не зависят от положения закрепленного контура по вертикали







![РезультатыНапряжение τrz в цилиндрических координатах вычисляется по формуле: τrz [r, z]=G( D[u[r, z], z]+ D[w[r, z],](/img/tmb/1/30767/f6ff93dd00a458dfa90af116c78a7656-800x.jpg)







