- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятие правильногомногогранника презентация
Содержание
- 1. Понятие правильногомногогранника
- 2. Одно из древнейших упоминаний о правильных многогранниках
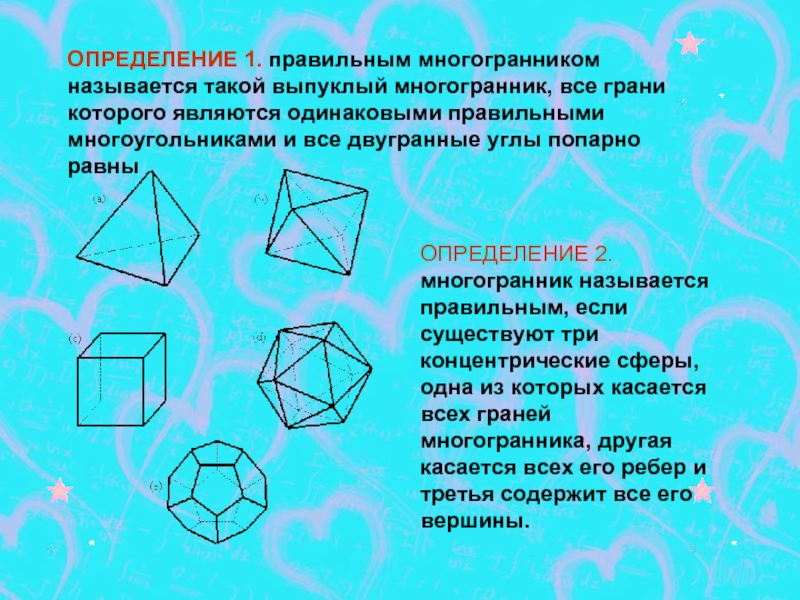
- 3. ОПРЕДЕЛЕНИЕ 1. правильным многогранником называется такой выпуклый
- 4. Если правильные многоугольники существуют с любым
- 5. Правильный тетраэдр составлен из четырех равносторонних треугольников.
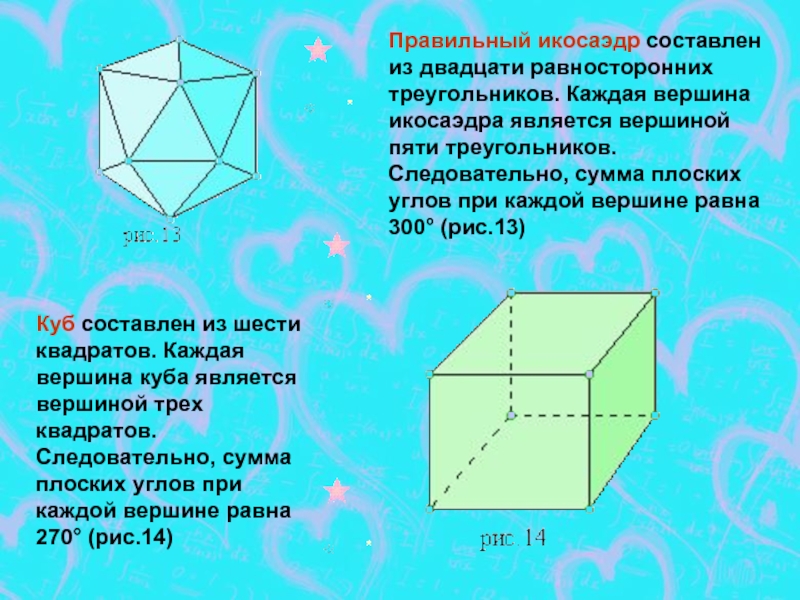
- 6. Правильный икосаэдр составлен из двадцати равносторонних треугольников.
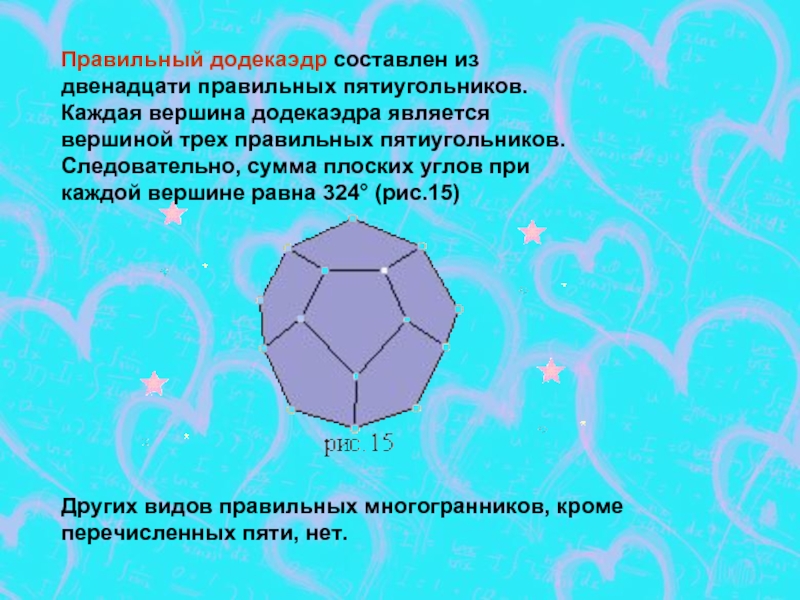
- 7. Правильный додекаэдр составлен из двенадцати правильных пятиугольников.
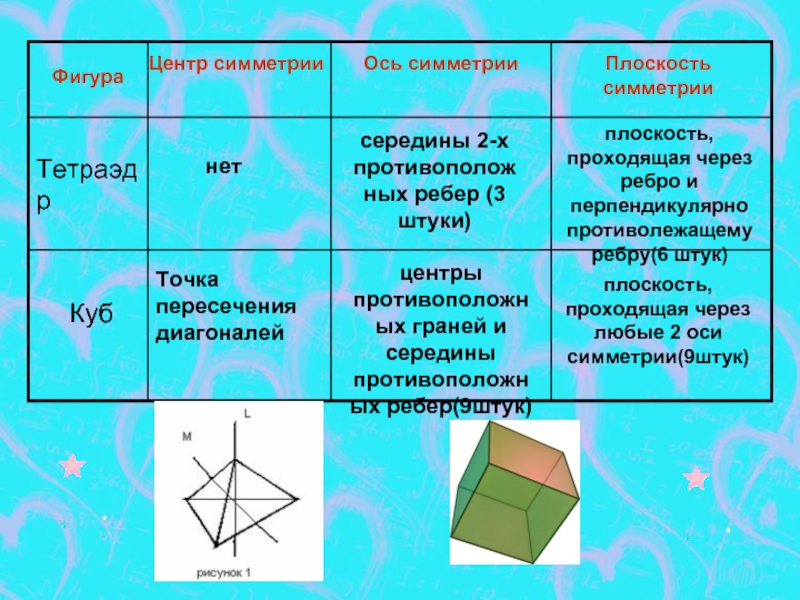
- 8. ЭЛЕМЕНТЫ СИММЕТРИИ ПРАВИЛЬНЫХ МНОГОГРАННИКОВ
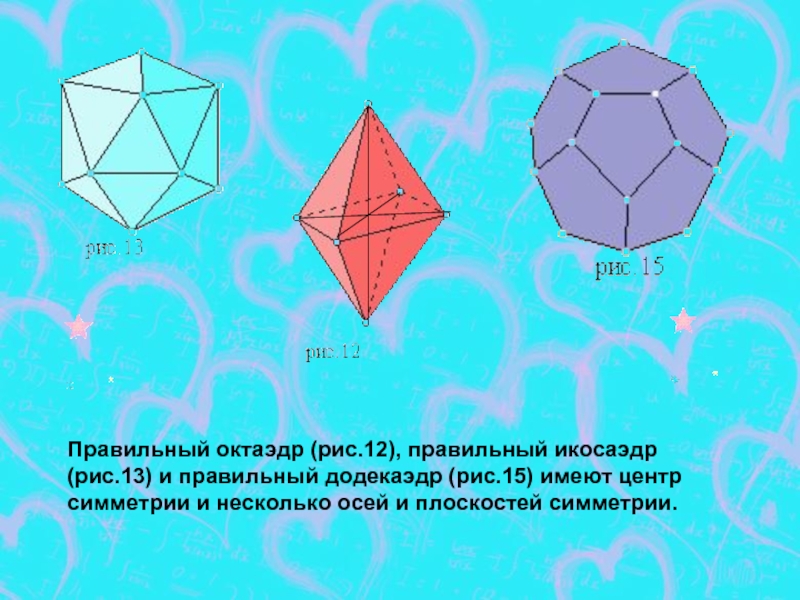
- 10. Правильный октаэдр (рис.12), правильный икосаэдр (рис.13) и
Слайд 2Одно из древнейших упоминаний о правильных многогранниках находится в трактате Платона
Слайд 3ОПРЕДЕЛЕНИЕ 1. правильным многогранником называется такой выпуклый многогранник, все грани которого
ОПРЕДЕЛЕНИЕ 2. многогранник называется правильным, если существуют три концентрические сферы, одна из которых касается всех граней многогранника, другая касается всех его ребер и третья содержит все его вершины.
Слайд 4 Если правильные многоугольники существуют с любым числом сторон n≥3, то
ДОКАЗАТЕЛЬСТВО.
Угол правильного n-угольника при n>=6 не меньше 180(n-2)/n => 180(6-2)/6=180*4/6=120 градусов. С другой стороны, при каждой вершине многогранника должно быть не менее трех плоских углов. Поэтому если бы существовал правильный многогранник, у которого грани – правильные n-угольники при n>=6, то сумма плоских углов при каждой вершине такого многогранника была бы не меньше чем 120*3=360 градусов. Но это невозможно, так как сумма всех плоских углов при каждой вершине выпуклого многогранника меньше 360 градусов.
Слайд 5Правильный тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является
Правильный октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех теугольников. Следовательно, сумма плоских углов при каждой вершине равна 240° (рис.12)
Слайд 6Правильный икосаэдр составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является
Куб составлен из шести квадратов. Каждая вершина куба является вершиной трех квадратов. Следовательно, сумма плоских углов при каждой вершине равна 270° (рис.14)
Слайд 7Правильный додекаэдр составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является
Других видов правильных многогранников, кроме перечисленных пяти, нет.