- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Показатели надежности презентация
Содержание
- 1. Показатели надежности
- 2. Функция отказа Q t 1
- 3. Введем понятие плотности вероятности отказа объекта f(t).
- 4. Плотность вероятности отказа f t
- 5. Обозначим вероятность безотказной работы в течение времени
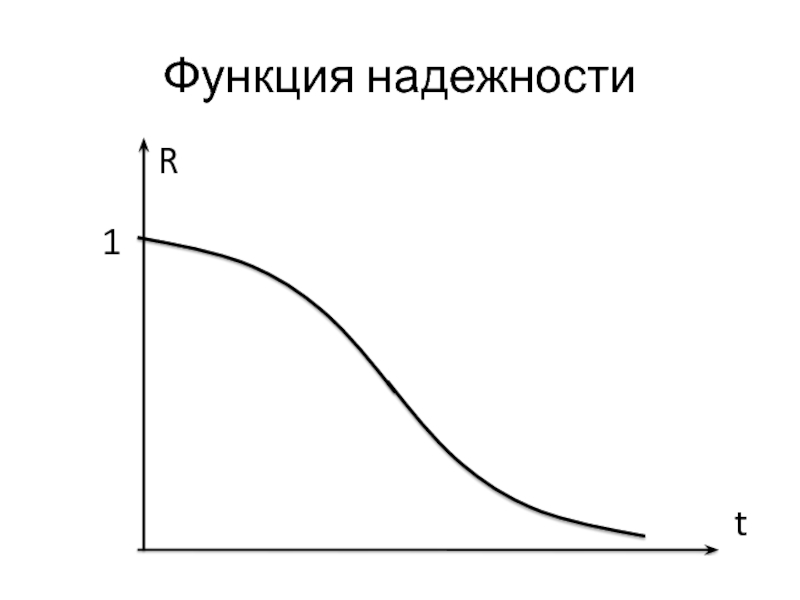
- 6. Функция надежности R t 1
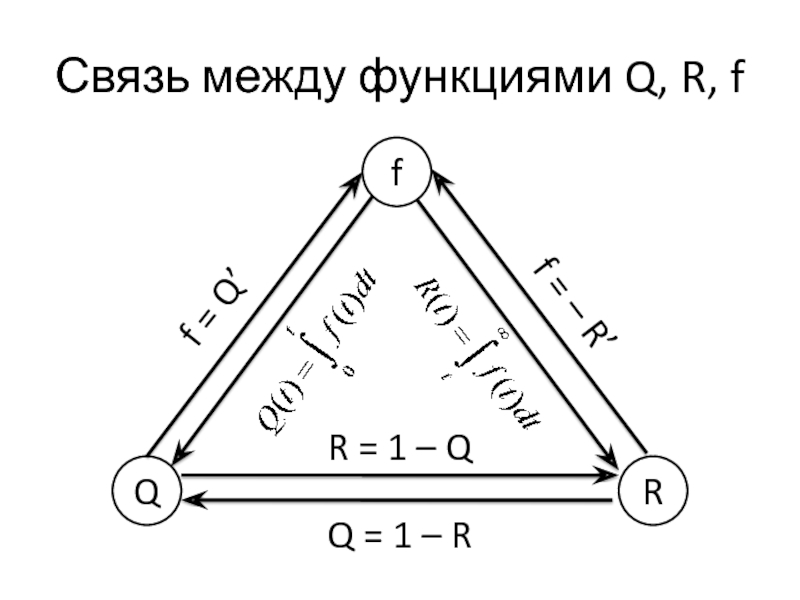
- 7. Связь между функциями Q, R, f Q
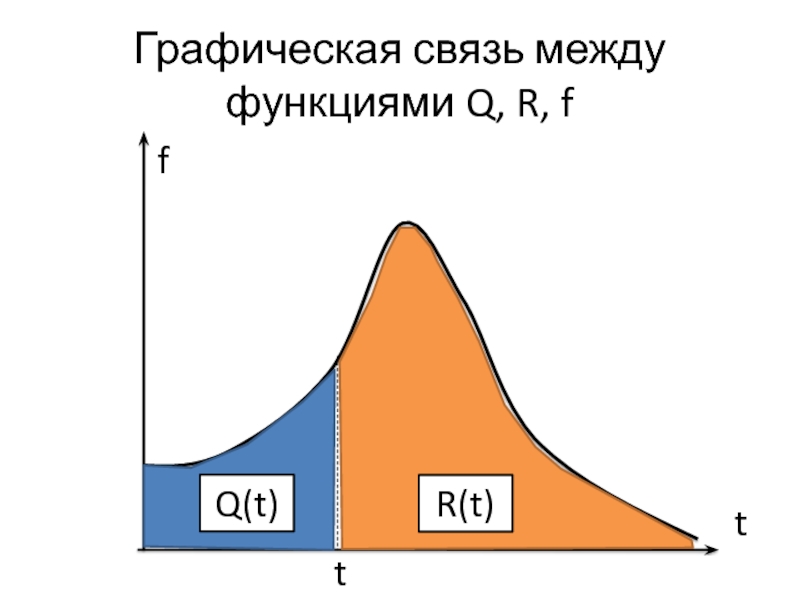
- 8. Графическая связь между функциями Q, R, f f t t Q(t) R(t)
- 9. Среднее время безотказной работы Т0 R t
- 10. Среднее время безотказной работы Т0 Статистически:
- 11. Среднее время безотказной работы Т0 Если нет
- 12. Интенсивность отказов λ(t) [λ] = с-1, ч-1,
- 13. Интенсивность отказов λ(t) Аналитически: Статистически: где m(Δt) – количество отказов за время Δt.
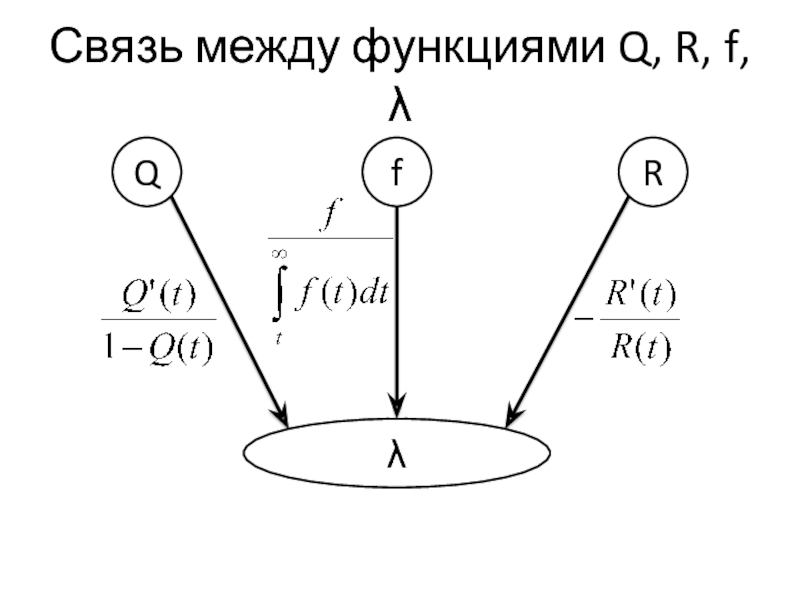
- 14. Связь между функциями Q, R, f, λ Q R f λ
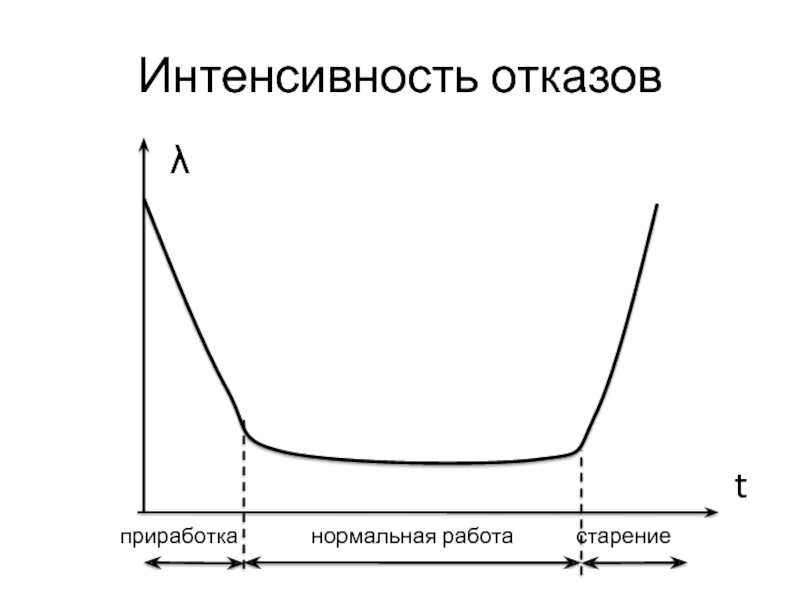
- 15. Интенсивность отказов λ t приработка нормальная работа старение
- 16. Рассмотрим нормальную работу Для нормальной работы можно
- 17. При экспоненциальном законе вероятность безотказной работы на
- 18. Упрощение формул для малых времён t В
- 19. 3.2. Объекты с мгновенным восстановлением Эксплуатация восстанавливаемого
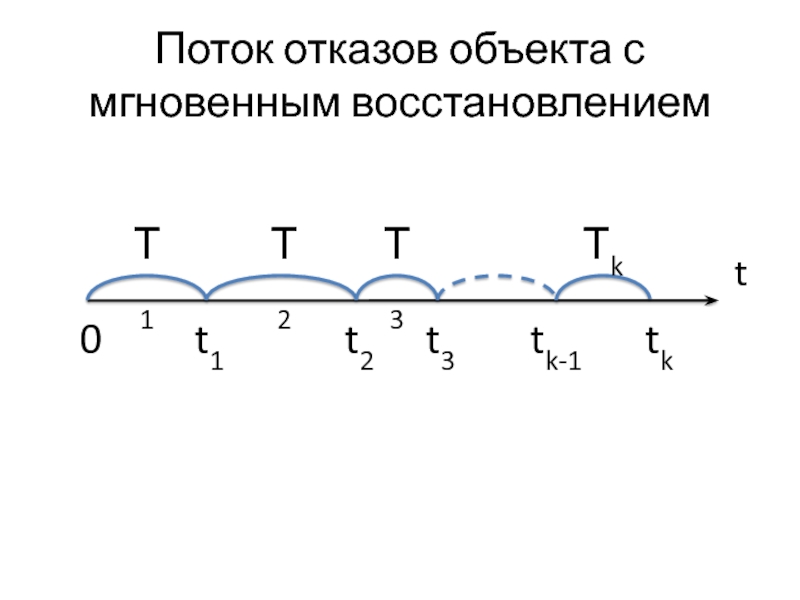
- 20. Поток отказов объекта с мгновенным восстановлением t
- 21. Рассмотрим плотности вероятностей времени: до первого отказа
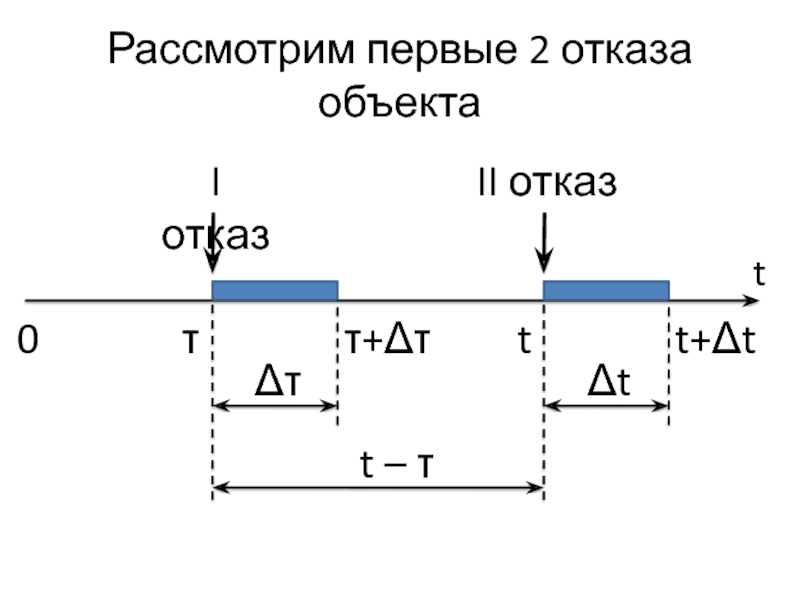
- 22. Рассмотрим первые 2 отказа объекта t I
- 23. Выведем формулу для f2(t) Наработка на второй
- 24. Обобщим этот результат на k отказов. Выведем
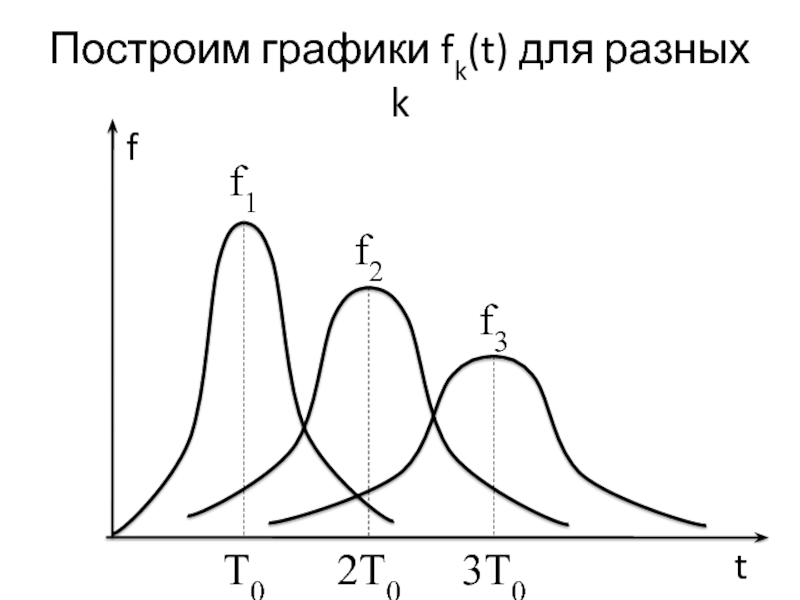
- 25. Построим графики fk(t) для разных k f
- 26. Свойства графиков fk(t) Каждый график fk(t) имеет
- 27. Параметр потока отказов ω(t) Назовём сумму f1(t)
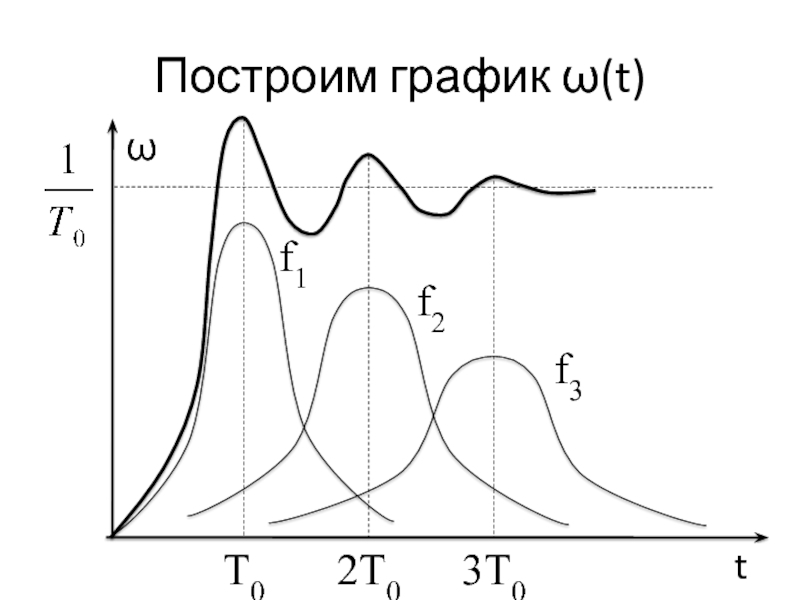
- 28. Построим график ω(t) ω t 2T0 T0
- 29. Свойство графика ω(t) График ω(t) имеет максимумы
- 30. Свойства потоков отказов Потоки отказов могут обладать
- 31. Виды потоков отказов Если выполняется (1),
- 32. Для простейшего потока: f1(t) = λ exp(–λt)
- 33. Для простейшего потока: Вероятность k отказов за
- 34. 3.3. Объекты с конечным временем восстановления Время
- 35. Поток отказов объекта с конечным временем восстановления
- 36. Сделаем допущения: 1) Тk, τk – независимые
- 37. Введём понятие коэффициента готовности Кг(t) Кг(t) –
- 38. Две гипотезы РСС объекта в момент времени
- 39. По формуле полной вероятности: Р(А) = Р(Н1)∙Р(А|Н1)
- 40. В разделе 3.1 доказано, что: R(Δt) =
- 41. Статистически:
- 42. Коэффициент неготовности – вероятность нахождения объекта в
Слайд 1Глава 3. Показатели надежности
3.1. Невосстанавливаемые объекты
Пусть при t = 0 объект
начинает работу;
при t = Т происходит отказ объекта.
Т – НСВ, которая называется наработка до отказа.
Обозначим функцию распределения этой НСВ Q(t).
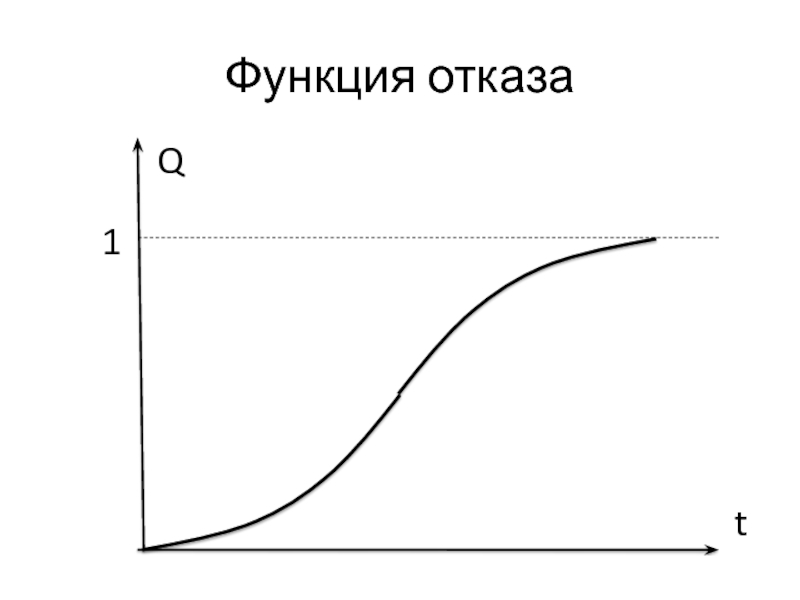
Назовём Q(t) функцией отказа.
По определению:
Q(t) = P(T < t) – вероятность отказа объекта до момента t.
при t = Т происходит отказ объекта.
Т – НСВ, которая называется наработка до отказа.
Обозначим функцию распределения этой НСВ Q(t).
Назовём Q(t) функцией отказа.
По определению:
Q(t) = P(T < t) – вероятность отказа объекта до момента t.
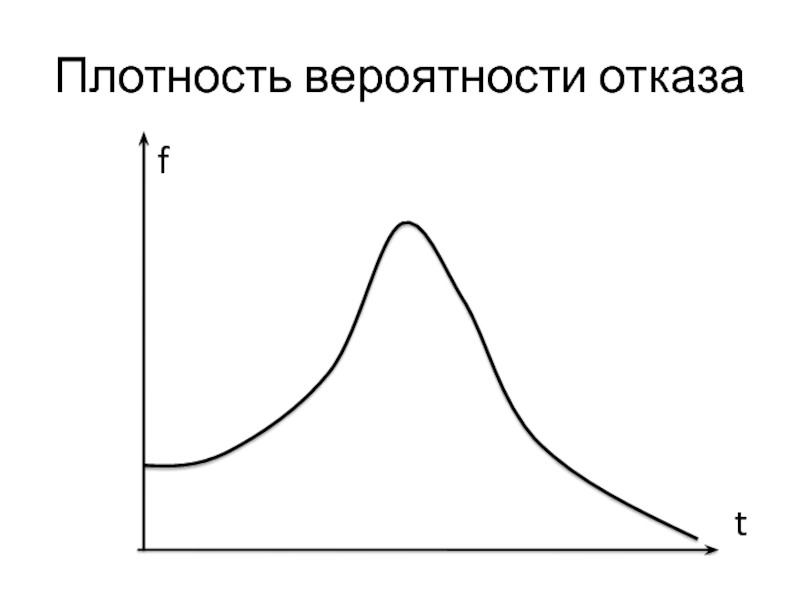
Слайд 3Введем понятие плотности вероятности отказа объекта f(t).
Аналитически:
f(t) = Q’(t).
Статистически:
где m(t)
– количество объектов, отказавших к моменту времени t;
N(t) – количество объектов, исправных к моменту времени t;
N0 – количество объектов, исправных при t = 0.
N(t) – количество объектов, исправных к моменту времени t;
N0 – количество объектов, исправных при t = 0.
Слайд 5Обозначим вероятность безотказной работы в течение времени t:
R(t) = P(T >
t)
Назовём R(t) функцией надежности.
Аналитически:
R(t) = 1 – Q(t).
Статистически:
Назовём R(t) функцией надежности.
Аналитически:
R(t) = 1 – Q(t).
Статистически:
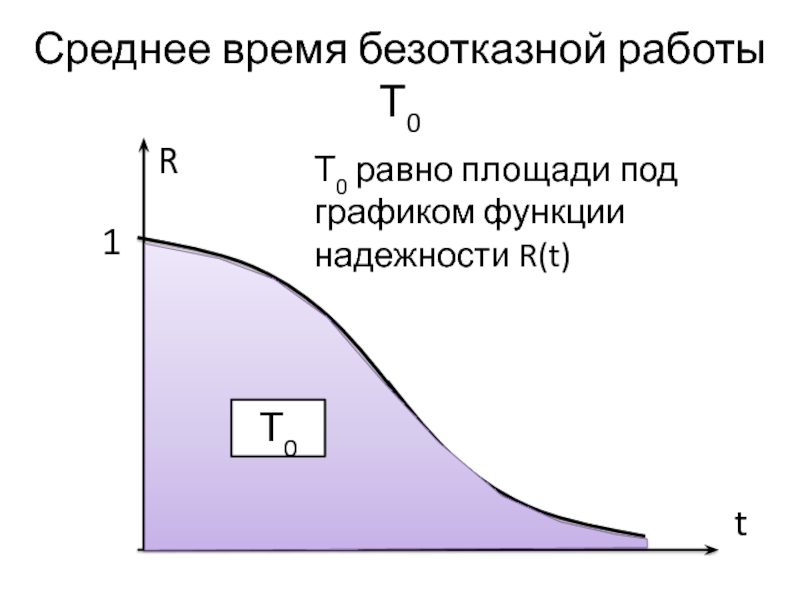
Слайд 9Среднее время безотказной работы Т0
R
t
1
Т0
Т0 равно площади под графиком функции надежности
R(t)
Слайд 10Среднее время безотказной работы Т0
Статистически:
где
ti – наработка до отказа i-го
объекта;
N0 – первоначальное количество исправных объектов.
Причём испытания проводят, пока все N0 объектов не откажут.
N0 – первоначальное количество исправных объектов.
Причём испытания проводят, пока все N0 объектов не откажут.
Слайд 11Среднее время безотказной работы Т0
Если нет возможности дожидаться отказа всех объектов
(из-за недостатка времени), то Т0 можно оценить так:
где
t – время испытания;
m – число отказавших объектов за время t
где
t – время испытания;
m – число отказавших объектов за время t
Слайд 12Интенсивность отказов λ(t)
[λ] = с-1, ч-1, год-1 и т. д.
Статистически:
λ(t) –
число отказов в единицу времени, отнесённое к числу безотказно проработавших до этого времени объектов.
С позиций теории вероятности:
λ(t) – условная плотность вероятности отказа объекта при условии, что до рассматриваемого момента отказа не было.
Таким образом λ(t) является локальной характеристикой надёжности, т.е. определяет надёжность объекта в каждый данный момент времени.
С позиций теории вероятности:
λ(t) – условная плотность вероятности отказа объекта при условии, что до рассматриваемого момента отказа не было.
Таким образом λ(t) является локальной характеристикой надёжности, т.е. определяет надёжность объекта в каждый данный момент времени.
Слайд 13Интенсивность отказов λ(t)
Аналитически:
Статистически:
где m(Δt) – количество отказов за время Δt.
Слайд 16Рассмотрим нормальную работу
Для нормальной работы можно считать:
λ(t) = const = λ
Тогда
R(t)
= exp(– λt)
Q(t) = 1 – exp(– λt)
f(t) = λexp(– λt)
T0 = 1/λ
Получили экспоненциальный закон распределения с параметром λ.
Q(t) = 1 – exp(– λt)
f(t) = λexp(– λt)
T0 = 1/λ
Получили экспоненциальный закон распределения с параметром λ.
Слайд 17При экспоненциальном законе вероятность безотказной работы на интервале (t; t +
Δt) не зависит от времени предшествующей работы t, а зависит только от продолжительности интервала Δt.
Доказательство:
По формуле условной вероятности
R(t; t + Δt) = R(t + Δt) / R(t) =
= exp(– λ(t + Δt)) / exp(– λt) =
= exp(– λ(t + Δt) + λt) = exp(– λΔt).
Доказательство:
По формуле условной вероятности
R(t; t + Δt) = R(t + Δt) / R(t) =
= exp(– λ(t + Δt)) / exp(– λt) =
= exp(– λ(t + Δt) + λt) = exp(– λΔt).
Слайд 18Упрощение формул для малых времён t
В практических расчетах при малых временах
рассмотренные выше формулы упрощают, используя соотношение из теории эквивалентов:
exp(x) ~ 1 + x при х → 0
Тогда
R(t) = 1 – λt
R(t; t + Δt) = 1 – λΔt
Q(t) = λt
Эти зависимости верны для малых λt (т.е. t << T0).
exp(x) ~ 1 + x при х → 0
Тогда
R(t) = 1 – λt
R(t; t + Δt) = 1 – λΔt
Q(t) = λt
Эти зависимости верны для малых λt (т.е. t << T0).
Слайд 193.2. Объекты с мгновенным восстановлением
Эксплуатация восстанавливаемого объекта не прекращается при его
отказе.
Объект ремонтируется или заменяется новым.
Наработка между отказами и продолжительность восстановления являются НСВ.
Рассмотрим ситуацию, когда время восстановления << наработки между отказами.
Объект ремонтируется или заменяется новым.
Наработка между отказами и продолжительность восстановления являются НСВ.
Рассмотрим ситуацию, когда время восстановления << наработки между отказами.
Слайд 21Рассмотрим плотности вероятностей времени:
до первого отказа f1(t);
до второго отказа f2(t);
…
до k-го
отказа fk(t).
Пусть первый отказ произошёл в момент τ;
пусть второй отказ произошёл в момент t.
Пусть первый отказ произошёл в момент τ;
пусть второй отказ произошёл в момент t.
Слайд 23Выведем формулу для f2(t)
Наработка на второй отказ равна t – τ.
Рассмотрим
вероятность того, что второй отказ произойдёт на интервале (t; t + Δt):
Δf2(t) Δt = f1(τ) Δτ ∙ f1(t – τ) Δt
Разделим на Δt и проинтегрируем по τ от 0 до t:
Δf2(t) Δt = f1(τ) Δτ ∙ f1(t – τ) Δt
Разделим на Δt и проинтегрируем по τ от 0 до t:
Слайд 24Обобщим этот результат на k отказов.
Выведем формулу для fk(t).
Пояснение:
Дошли до (k
– 1)-го отказа,
зафиксировали накопившуюся вероятность
и начали отсчёт времени с нуля.
Значит, следующий отказ будет первым =>
=> в интеграле имеется f1(t).
зафиксировали накопившуюся вероятность
и начали отсчёт времени с нуля.
Значит, следующий отказ будет первым =>
=> в интеграле имеется f1(t).
Слайд 26Свойства графиков fk(t)
Каждый график fk(t) имеет максимум в точке
t =
kТ0.
Каждый график fk(t) приблизительно симметричен относительно оси t = kТ0.
Максимальное значение функции fk(t) уменьшается с ростом k, т.к. накапливаются неопределённости по предыдущим наработкам.
Кривая fk(t) становится более пологой (широкой) с ростом k.
Каждый график fk(t) приблизительно симметричен относительно оси t = kТ0.
Максимальное значение функции fk(t) уменьшается с ростом k, т.к. накапливаются неопределённости по предыдущим наработкам.
Кривая fk(t) становится более пологой (широкой) с ростом k.
Слайд 27Параметр потока отказов ω(t)
Назовём сумму
f1(t) + f2(t) + … + fk(t)
= ω(t)
параметром потока отказов.
По сути ω(t) – это плотность вероятности отказа.
С одной стороны функция ω(t) является локальной по времени, с другой стороны она охватывает одновременно все отказы, т.е. является глобальной по отказам.
параметром потока отказов.
По сути ω(t) – это плотность вероятности отказа.
С одной стороны функция ω(t) является локальной по времени, с другой стороны она охватывает одновременно все отказы, т.е. является глобальной по отказам.
Слайд 29Свойство графика ω(t)
График ω(t) имеет максимумы в точках
t = kТ0.
Кривая
ω(t) стабилизируется с течением времени и с ростом k на уровне 1/Т0, т.е. процесс возникновения отказов становится стационарным, его локальные характеристики перестают зависеть от времени.
Слайд 30Свойства потоков отказов
Потоки отказов могут обладать свойствами:
Свойство ординарности. Вероятность совмещение 2-х
и более отказов в один момент времени равна нулю.
Свойство отсутствия последействия. Числа отказов для любых неперекрывающихся интервалов времени независимы.
Свойство стационарности. Вероятность появления k отказов на любом промежутке времени зависит только от числа k и от длительности Δt и не зависит от начала отсчёта времени.
Свойство отсутствия последействия. Числа отказов для любых неперекрывающихся интервалов времени независимы.
Свойство стационарности. Вероятность появления k отказов на любом промежутке времени зависит только от числа k и от длительности Δt и не зависит от начала отсчёта времени.
Слайд 31Виды потоков отказов
Если выполняется (1),
то поток ординарный.
Если выполняются (1) и
(2),
то поток пуассоновский.
Если выполняются (1), (2), (3), то поток простейший.
Если выполняются (1), (2), (3), то поток простейший.
Слайд 33Для простейшего потока:
Вероятность k отказов за время t:
Вероятность безотказной работы за
время t:
P0(t) = exp(–λt)
P0(t) = exp(–λt)
Слайд 343.3. Объекты с конечным временем восстановления
Время восстановления τ = tп +
tр
tп – поиск неисправности;
tр – ремонт или замена.
Пусть объект, проработав время T1, выходит из строя и восстанавливается в течение τ1.
Восстановленный объект через T2 вновь отказывает, за τ2 снова восстанавливается и т.д.
tп – поиск неисправности;
tр – ремонт или замена.
Пусть объект, проработав время T1, выходит из строя и восстанавливается в течение τ1.
Восстановленный объект через T2 вновь отказывает, за τ2 снова восстанавливается и т.д.
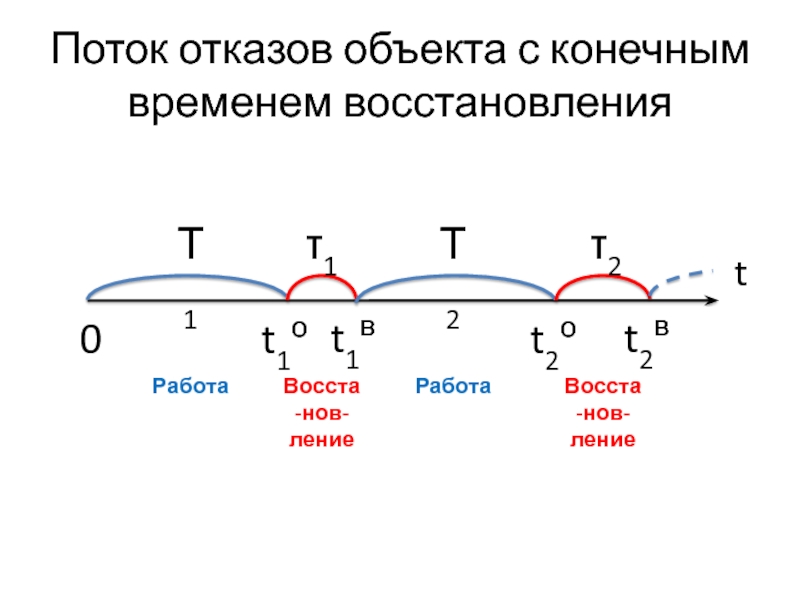
Слайд 35Поток отказов объекта с конечным временем восстановления
t
Т1
τ1
Т2
τ2
t1о
0
t1в
t2о
t2в
Работа
Восста-нов-ление
Работа
Восста-нов-ление
Слайд 36Сделаем допущения:
1) Тk, τk – независимые НСВ.
2) Все периоды работы Тk
имеют:
- законы F(t), f(t);
- среднюю наработку на отказ Т = М(Тk);
- интенсивность отказов λ = 1/Т.
3) Все периоды восстановления τk имеют: - законы G(t), g(t); - среднее время восстановления τ = М(τk) ; - интенсивность восстановлений μ = 1/τ.
4) Поток отказов и восстановлений – простейший.
3) Все периоды восстановления τk имеют: - законы G(t), g(t); - среднее время восстановления τ = М(τk) ; - интенсивность восстановлений μ = 1/τ.
4) Поток отказов и восстановлений – простейший.
Слайд 37Введём понятие коэффициента готовности Кг(t)
Кг(t) – это вероятность того, что в
момент времени t объект находится в работоспособном состоянии (РСС).
Найдём зависимость Кг(t).
Вероятность застать объект в РСС в момент (t + Δt) зависит от его состояния в момент t и его поведения на интервале Δt.
Найдём зависимость Кг(t).
Вероятность застать объект в РСС в момент (t + Δt) зависит от его состояния в момент t и его поведения на интервале Δt.
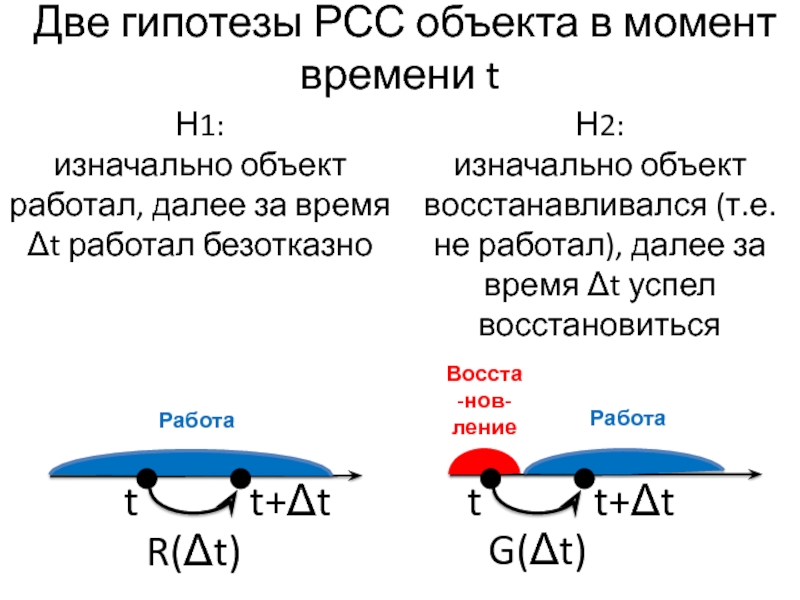
Слайд 38Две гипотезы РСС объекта в момент времени t
t
Работа
Работа
Восста-нов-ление
t+Δt
t
t+Δt
Н1:
изначально объект работал, далее
за время Δt работал безотказно
Н2:
изначально объект восстанавливался (т.е. не работал), далее за время Δt успел восстановиться
R(Δt)
G(Δt)
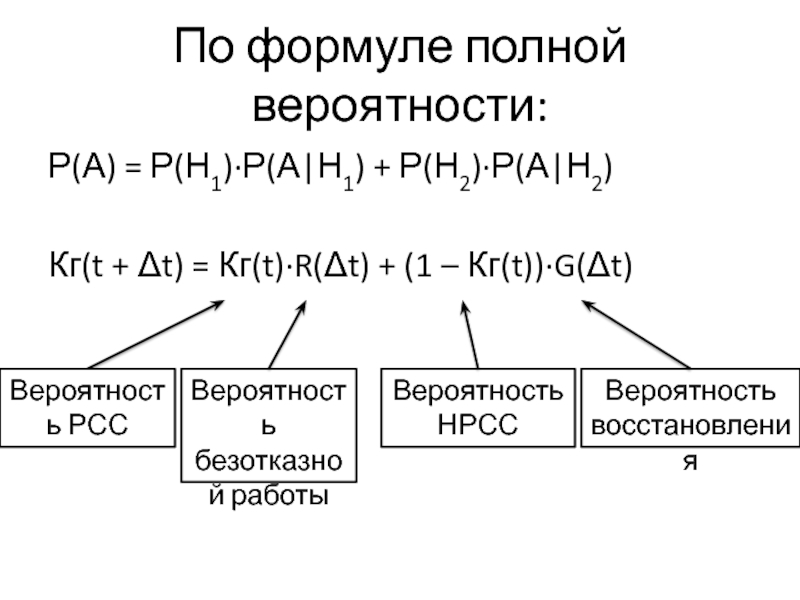
Слайд 39По формуле полной вероятности:
Р(А) = Р(Н1)∙Р(А|Н1) + Р(Н2)∙Р(А|Н2)
Кг(t + Δt)
= Кг(t)∙R(Δt) + (1 – Кг(t))∙G(Δt)
Вероятность РСС
Вероятность безотказной работы
Вероятность НРСС
Вероятность восстановления
Слайд 42Коэффициент неготовности – вероятность нахождения объекта в НРСС.
Кнг = 1 –
Кг
Кнг(0) = 0
Кнг(∞) = λ/(λ+μ) = τ/(Т+τ)
график Кнг(t)
Коэффициент аварийного простоя – относительная длительность восстановления.
qав = λ/μ = τ/Т
Кнг(0) = 0
Кнг(∞) = λ/(λ+μ) = τ/(Т+τ)
график Кнг(t)
Коэффициент аварийного простоя – относительная длительность восстановления.
qав = λ/μ = τ/Т





![Интенсивность отказов λ(t)[λ] = с-1, ч-1, год-1 и т. д.Статистически:λ(t) – число отказов в единицу](/img/tmb/5/464907/7afe815482f7f48544b8aadee7ecafc0-800x.jpg)