- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Подготовка школьников к предметным олимпиадам по математике презентация
Содержание
- 1. Подготовка школьников к предметным олимпиадам по математике
- 2. а Система работы с одаренными детьми
- 3. а Работа олимпиадных элективных занятий строится
- 4. а Трудно рекомендовать какой-либо общий план
- 5. а Учителю математики, занимающемуся подготовкой учащихся
- 6. а Из каждого раздела не
- 7. а При непосредственной подготовке учащихся к
- 8. а Свойства четных и нечетных чисел
- 9. а Задачи
- 10. а Задачи
- 11. Задачи
- 12. а Тема:
- 13. а Тема: Делимость чисел Свойства делимости
- 14. а Задачи
- 15. а Задачи 11) 1) 1) 2)
- 16. а 3) Докажите, что при любом
- 17. а Задачи 11) 3) 11) 4)
- 18. а Тема: Неравенства в целых числах
- 19. а Тема: Доказательство неравенств
- 20. а Задачи Докажите, что если
- 21. а Задачи Докажите, что если
- 22. а Задачи Решение
- 23. а Тема:
- 24. а Задачи Уравнения, которые содержат квадрат только одного неизвестного
- 25. Задачи Уравнения, которые содержат квадраты обоих неизвестных
- 26. Задачи Решите в целых числах уравнение
- 27. Задачи Решите в целых числах уравнение
- 28. Задачи Уравнения, которые не имеют решений
- 29. Задачи Уравнения, которые не имеют решений 1) 2)
- 30. рекомендации учителям, работающим над подготовкой к олимпиадам
- 31. http://www. mathematics. ru - Математика в
Слайд 1
Подготовка школьников к предметным олимпиадам по математике
МБОУ «КРАСНОСЛОБОДСКИЙ МНОГОПРОФИЛЬНЫЙ ЛИЦЕЙ»
Подготовила:
Пузина Надежда Васильевна
учитель математики
высшей квалификационной категории
Слайд 2а
Система работы с одаренными детьми включает в себя следующие компоненты:
развитие творческих способностей на
уроках;
развитие способностей во внеурочной
деятельности (олимпиады, конкурсы,
исследовательская работа);
создание условий для всестороннего
развития одаренных детей.
Слайд 3а
Работа олимпиадных элективных занятий строится на следующих принципах
1.
2. Принцип параллельности.
3. Принцип опережающей сложности.
4. Принцип смены приоритетов.
5. Принцип вариативности.
6. Принцип самоконтроля.
7. Принцип работы с текстом.
Слайд 4а
Трудно рекомендовать какой-либо общий план элективного занятия – форма их может
Занятия могут проходить в виде:
лекции или семинара, олимпиады, математической регаты или математического боя, командного соревнования по решению задач
Планирование элективных занятий тоже должно носить гибкий характер: неожиданно возникший на уроке вопрос может послужить темой ближайшего занятия.
Слайд 5а
Учителю математики, занимающемуся подготовкой учащихся к олимпиадам необходимо обеспечить работу с
1. Ребусы, криптограммы.
2. Текстовые задачи.
3. Теория чисел.
4. Планиметрия.
5. Стереометрия.
6. Уравнения, неравенства и системы.
7. Доказательства числовых неравенств.
8. Задачи на взвешивание.
9. Логические задачи.
10. Комбинаторные задачи.
Слайд 6а
Из каждого раздела не стоит рассматривать случайную выборку задач, нужно
1. Восстановление знаков действий.
2. Восстановление цифр натуральных чисел.
3. Числовые ребусы.
4. Четные и нечетные числа.
5. Признаки делимости.
6. Простые и составные числа.
7. Деление с остатком.
8. Перестановка и зачеркивание цифр в натуральном числе.
9. Последние цифры натурального числа.
10. Степень с натуральным показателем.
11. Системы счисления.
12. Уравнения в целых числах.
13. Неравенства в целых числах.
Слайд 7а
При непосредственной подготовке учащихся к математическим конкурсам и олимпиадам необходимо акцентировать
в задачах на доказательство требуется полное
обоснование
если в условии требуется указать все возможные
способы решения, то от полноты количества указанных
способов зависит и количество полученных баллов
если в условии требуется ответить на вопрос «Можно
ли…?», то для ответа достаточно привести один
положительный пример, а для того, чтобы дать ответ
«нельзя». Необходимо рассмотреть все возможные
случаи, обобщая их в доказательство
Слайд 8а
Свойства четных и нечетных чисел
Тема: Четные и нечетные
Разность четна, если числа а и b одинаковой четности , (тогда эта разность делится на 4) и нечетна, если числа а и b разной четности
Слайд 16а
3) Докажите, что при любом целом m выражение m3 + 17m
Доказательство
m3 + 17m = m3 – m + 18m = (m – 1)m(m + 1) + 18m, т.к. (m – 1)m(m + 1) делится на 6 и 18m делится на 6, то и все выражение делится на 6.
Произведение трех последовательных целых чисел делится на 6 ( по задаче 2)
Задачи
Слайд 19а
Тема: Доказательство неравенств
Часто при доказательстве неравенств используются формулы
(частные
Слайд 20а
Задачи
Докажите, что если a > 0, b> 0, c> 0,
Доказательство
Перемножим неравенства
Слайд 21а
Задачи
Докажите, что если a > 0, b> 0, то (a
Доказательство
Перемножим неравенства
Слайд 22а
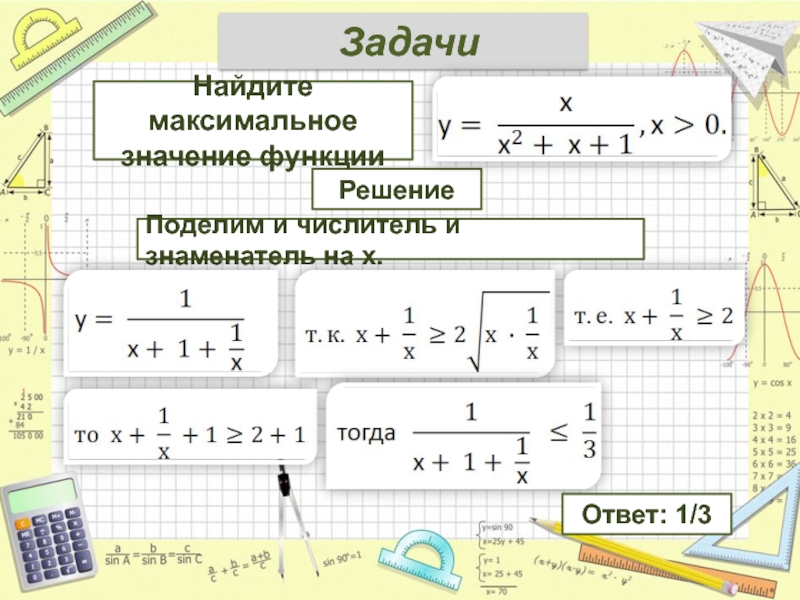
Задачи
Решение
Найдите максимальное значение функции
Поделим и числитель и знаменатель на х.
Ответ:
Слайд 23а
Тема: Уравнения в целых числах
11))
Уравнения, которые не
Слайд 26 Задачи
Решите в целых числах уравнение
х2 + у2 = 2
1 способ(нерациональный) х2 - х + у2 - у – 2 = 0
Откуда - 4у2 + 4у +9 ≥ 0
т.е. у = -1, 0, 1, 2, подставляя вместо у эти значения получим решения: (1;-1), (0;-1), (2;0), (-1;0), (2;1), (-1;1), (1;2), (0;2)
Решение
Слайд 27 Задачи
Решите в целых числах уравнение
х2 + у2 = 2
2 способ(рациональный) (х2 – х) + (у2 – у) = 2
х2 – х = х(х-1) и у2 – у = у(у-1) - четные числа, т.к. х2 – х ≥0 и у2 – у ≥ 0 , то
либо х2 – х = 0, у2 – у = 2,
либо х2 – х = 2, у2 – у = 0
получим решения:
(1;-1), (0;-1), (2;0), (-1;0), (2;1), (-1;1), (1;2), (0;2)
Решение
Слайд 28 Задачи
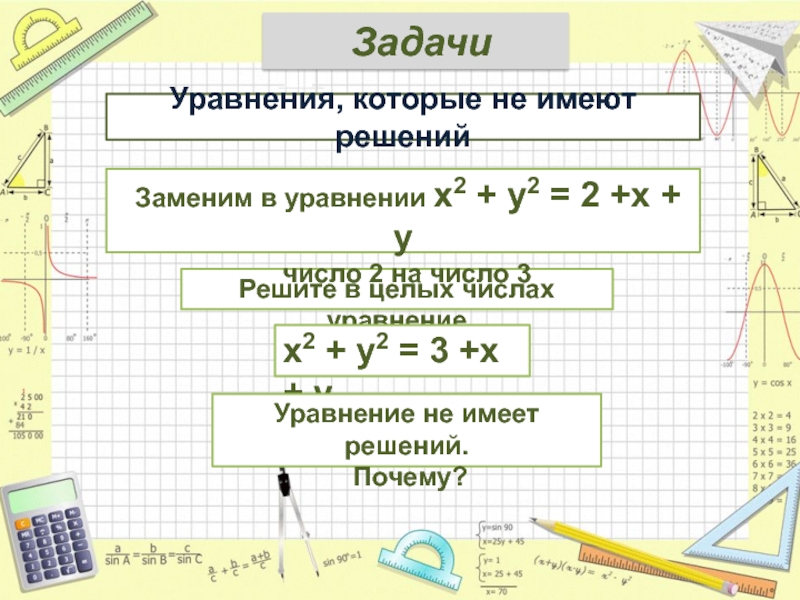
Уравнения, которые не имеют решений
Решите в целых числах уравнение
х2
Заменим в уравнении х2 + у2 = 2 +х + у
число 2 на число 3
Уравнение не имеет решений.
Почему?
Слайд 30рекомендации учителям, работающим над подготовкой к олимпиадам одаренных детей
1. необходимо усиливать
2. при подготовке уделять особое внимание геометрическим нестандартным задачам, способу доказательства от противного и смешанным задачам (комбинаторика и теория чисел и др.),
3. усилить изучение внепрограммного материала: теория чисел и логические задачи с шахматами),
4. обращать внимание на специфику решения задач с параметрами и на интеграцию геометрии и комбинаторики.
5. создавать индивидуальные траектории подготовки к олимпиадам
6. готовить задачи с измененным условием
7. развивать мышление одаренных детей в направлении культуры алгоритмизации и пространственного мышления
8. формировать навыки исследования,
9. использовать склонность одаренных детей к самообучению.
Заключение
Слайд 31 http://www. mathematics. ru - Математика в Открытом колледже
http://www. allmath.
http://www. eqworld. ipmnet. ru - EqWorld: Мир математических уравнений
http://www. exponenta. ru - Exponenta.ru: образовательный математический сайт
http://www. neive. by. ru - Геометрический портал
http://www. graphfunk. narod. ru - Графики функций
http://www. uztest. ru - ЕГЭ по математике: подготовка к тестированию
http://www. tasks. ceemat. ru - Задачник для подготовки к олимпиадам по математике
http://www. math-on-line. com - Занимательная математика — школьникам (олимпиады, игры,
конкурсы по математике)
http://www. problems. ru - Интернет-проект «Задачи»
http://www. etudes. ru - Математические этюды
http://www. mathem. h1.ru - Математика on-line: справочная информация в помощь студенту
http://www. mathtest. ru - Математика в помощь школьнику и студенту (тесты по математике
online)
http://www. matematika. agava. ru - Математика для поступающих в вузы
http://www. zaba. ru - Математические олимпиады и олимпиадные задачи
http://www. kenguru. sp. ru - Международный математический конкурс «Кенгуру»
http://www. olympiads. mccme. ru/mmo - Московская математическая олимпиада школьников
http://www. mathnet. spb. ru - Сайт элементарной математики Дмитрия Гущина
http://www. turgor. ru - Турнир городов — Международная математическая олимпиада для
школьников
Список ресурсов