- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Периметр и площадь презентация
Содержание
- 1. Периметр и площадь
- 2. Что же такое периметр? Периметр — общая
- 3. Кое-что интересное В Древнем мире теория измерений
- 4. Формулы для нахождения периметра Периметр фигуры =
- 5. Теперь поговорим о площади Площадь фигуры — числовая
- 6. Немного об истории площади и вообще геометрии в других странах и в другое время
- 7. Египет В Древнем Египте в области геометрии
- 8. Вавилон В геометрии рассматривались те же фигуры,
- 9. Древняя Греция Древнеегипетскую и вавилонскую культуру в
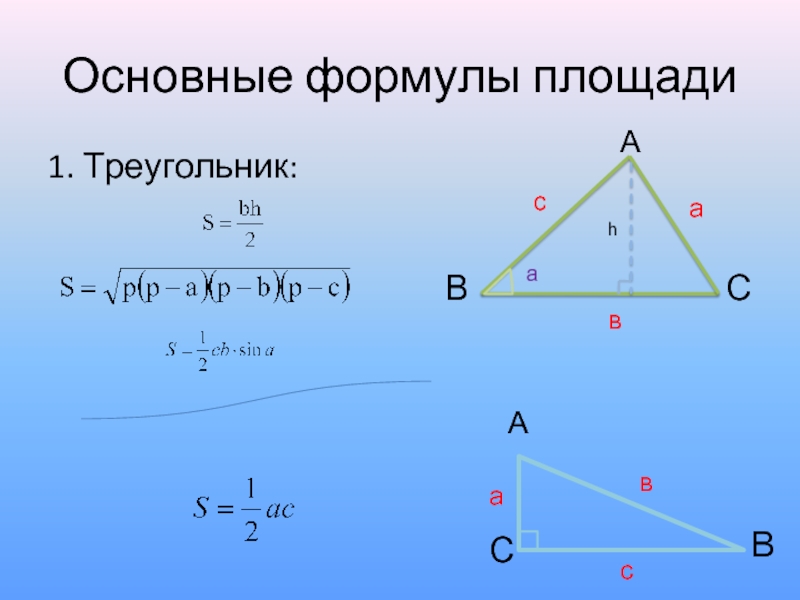
- 10. Основные формулы площади 1. Треугольник:
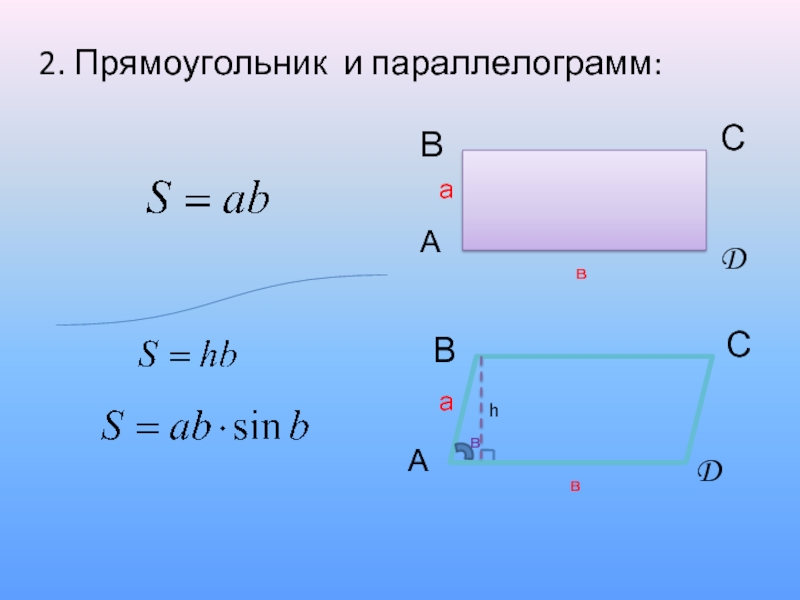
- 11. 2. Прямоугольник и параллелограмм: в
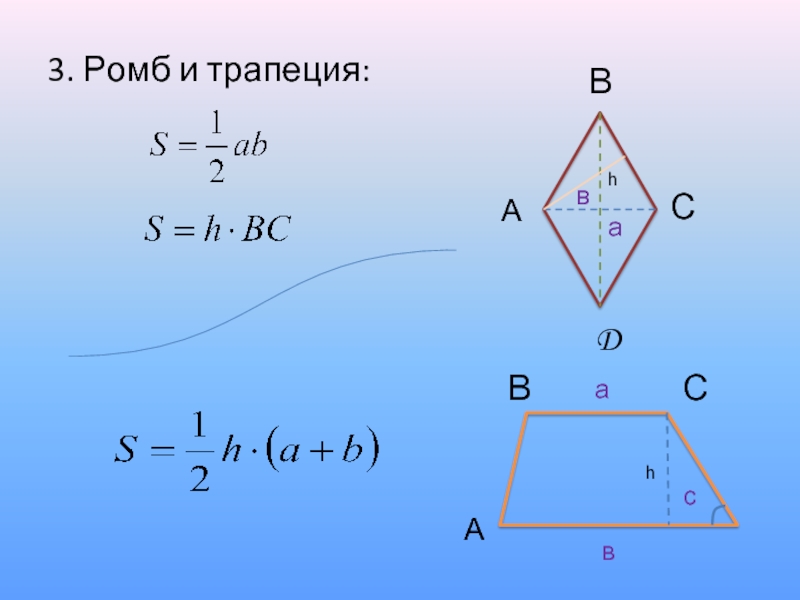
- 12. 3. Ромб и трапеция: с
- 13. Круг, Круговой сектор a r
- 14. Площадь можно измерить с помощью разделения на
- 15. Конец
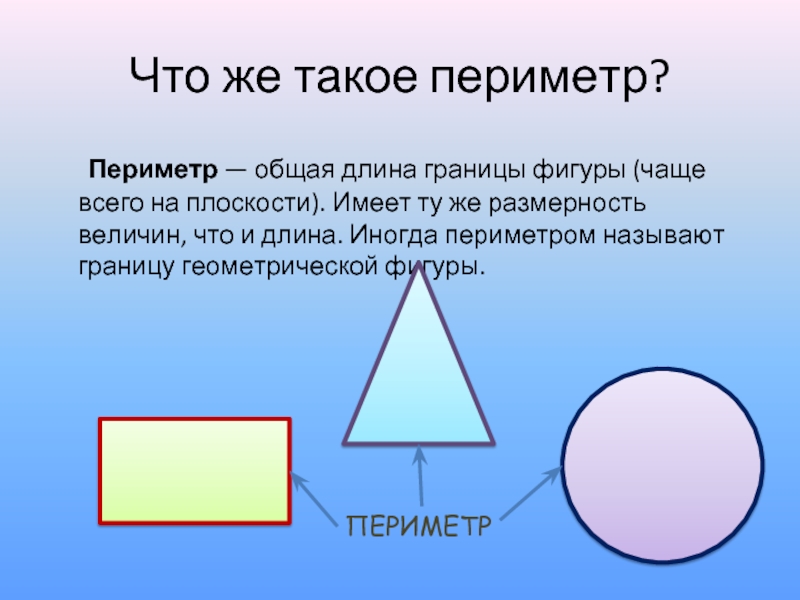
Слайд 2Что же такое периметр?
Периметр — общая длина границы фигуры (чаще всего
на плоскости). Имеет ту же размерность величин, что и длина. Иногда периметром называют границу геометрической фигуры.
ПЕРИМЕТР
Слайд 3Кое-что интересное
В Древнем мире теория измерений нередко содержала ошибки: характерным примером
является ложное учение о равенстве площадей фигур при равенстве их периметров, и обратно. Это неудивительно: измерительным инструментом служила мерная верёвка с узлами или пометками, так что измерить периметр можно было без труда, а для определения площади в общем случае ни инструментов, ни математических методов не было. Измерения служили важнейшим применением дробных чисел и источником развития их теории.
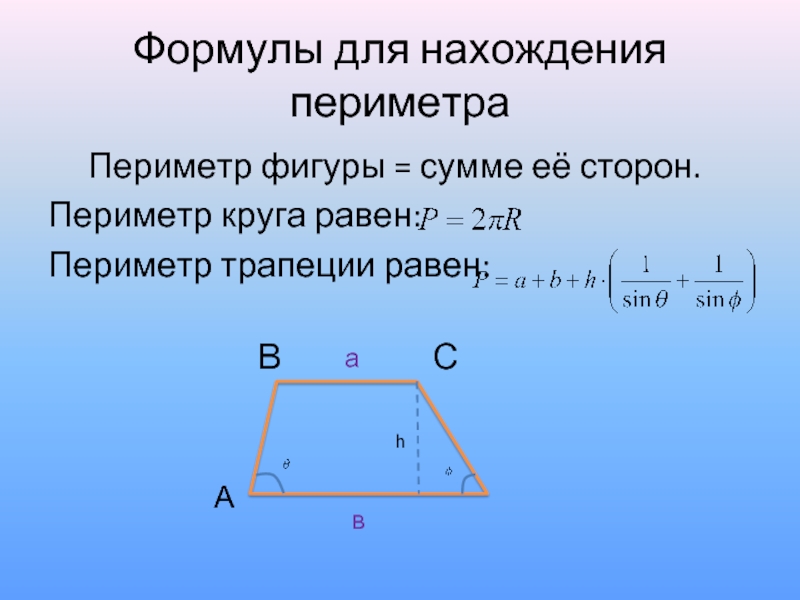
Слайд 4Формулы для нахождения периметра
Периметр фигуры = сумме её сторон.
Периметр круга равен:
Периметр
трапеции равен:
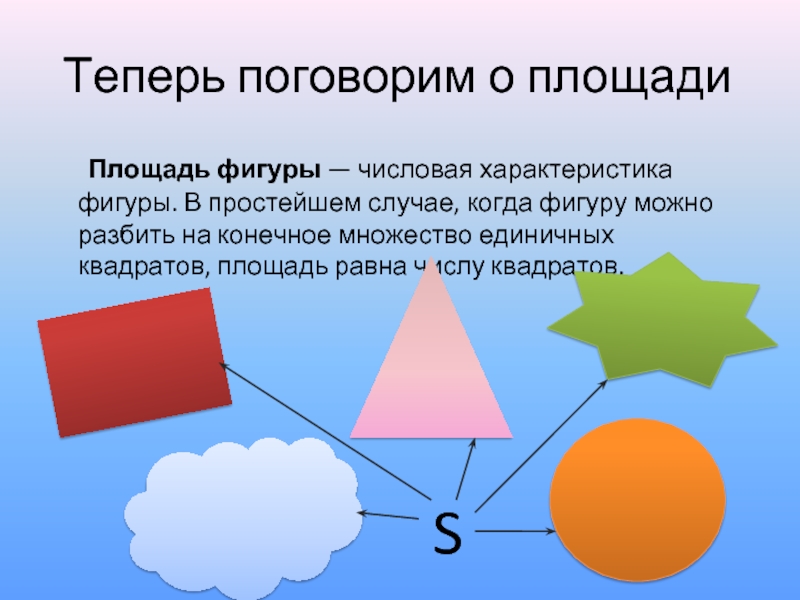
Слайд 5Теперь поговорим о площади
Площадь фигуры — числовая характеристика фигуры. В простейшем случае,
когда фигуру можно разбить на конечное множество единичных квадратов, площадь равна числу квадратов.
Слайд 7Египет
В Древнем Египте в области геометрии египтяне точно знали формулы для
нахождения площади прямоугольника, треугольника и трапеции. Площадь произвольного четырёхугольника со сторонами a, b, c, d вычислялась приближённо как ; эта грубая формула даёт приемлемую точность, если фигура близка к прямоугольнику. Площадь круга вычислялась, исходя из предположения: (погрешность менее 1 %).
Слайд 8Вавилон
В геометрии рассматривались те же фигуры, что и в Египте, плюс
сегмент круга и усечённый конус. В ранних документах полагают π = 3; позже встречается приближение 25/8 = 3,125. Вавилоняне умели вычислять площади правильных многоугольников; видимо, им был знаком принцип подобия. Для площади неправильных четырёхугольников использовалась та же приближённая формула, что и в Египте:
Венцом геометрии была теорема Пифагора, известная ещё в эпоху Хаммурапи.
Всё же богатая теоретическая основа математики Вавилона не имела целостного характера и сводилась к набору разрозненных приёмов, лишённых доказательной базы.
Венцом геометрии была теорема Пифагора, известная ещё в эпоху Хаммурапи.
Всё же богатая теоретическая основа математики Вавилона не имела целостного характера и сводилась к набору разрозненных приёмов, лишённых доказательной базы.
Слайд 9Древняя Греция
Древнеегипетскую и вавилонскую культуру в области математики продолжали греки. Они
не только усвоили весь опыт их геометрии, но и пошли гораздо дальше. Ученые древней Греции сумели привести в систему накопленные геометрические знания и, таким образом, заложить начала геометрии как дедуктивной науки.
Греческие купцы познакомились с восточной математикой, прокладывая торговые пути. Но люди Востока почти не занимались теорией, и греки быстро это обнаружили. Они задавались вопросами: почему в равнобедренном треугольнике два угла при основании равны; почему площадь треугольника равна половине площади прямоугольника при одинаковых основаниях и высотах?
Первой среди научных и философских школ древней Греции была ионийская (VI в. до н.э.). Ее ученые впервые стали заниматься геометрией, однако строгой геометрической системы не создали. У них имелось лишь собрание правил, найденных эмпирическим путем, которыми они пользовались при конкретных построениях.
После падения Милета, развитие математики происходило в другой древнегреческой школе, основателем которой был легендарный Пифагор (564-473 г.г. до н. э.).
Греческие купцы познакомились с восточной математикой, прокладывая торговые пути. Но люди Востока почти не занимались теорией, и греки быстро это обнаружили. Они задавались вопросами: почему в равнобедренном треугольнике два угла при основании равны; почему площадь треугольника равна половине площади прямоугольника при одинаковых основаниях и высотах?
Первой среди научных и философских школ древней Греции была ионийская (VI в. до н.э.). Ее ученые впервые стали заниматься геометрией, однако строгой геометрической системы не создали. У них имелось лишь собрание правил, найденных эмпирическим путем, которыми они пользовались при конкретных построениях.
После падения Милета, развитие математики происходило в другой древнегреческой школе, основателем которой был легендарный Пифагор (564-473 г.г. до н. э.).
Слайд 14Площадь можно измерить с помощью разделения на квадраты.
Но этот способ больше
подходит для начальной школы.