- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Переход Андерсона:теория и численный экспериментИ.М.СусловИнститут физических проблем им. П.Л.Капицы РАН презентация
Содержание
- 1. Переход Андерсона:теория и численный экспериментИ.М.СусловИнститут физических проблем им. П.Л.Капицы РАН
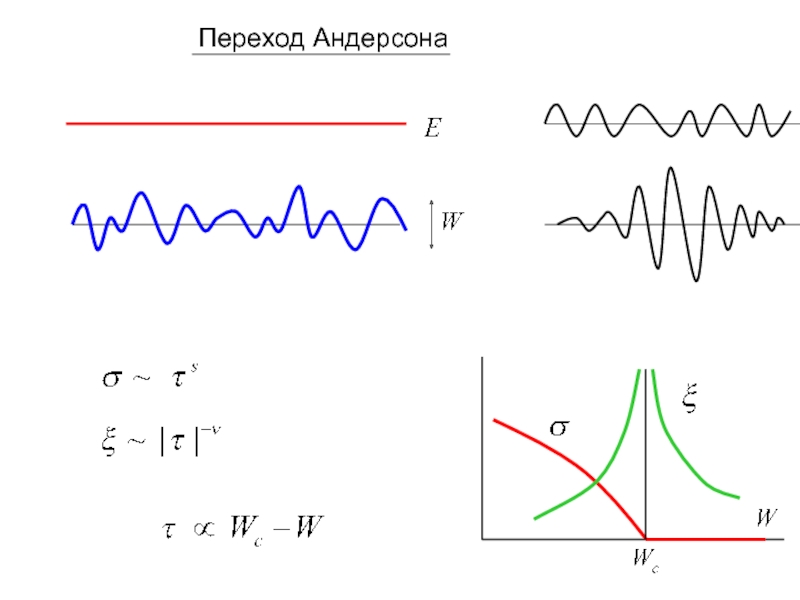
- 2. Переход Андерсона
- 3. Современная ситуация: Численный счет противоречит всей
- 4. Самосогласованная теория Вольхардта-Вольфле дает результат
- 5. Гипотеза о том, что
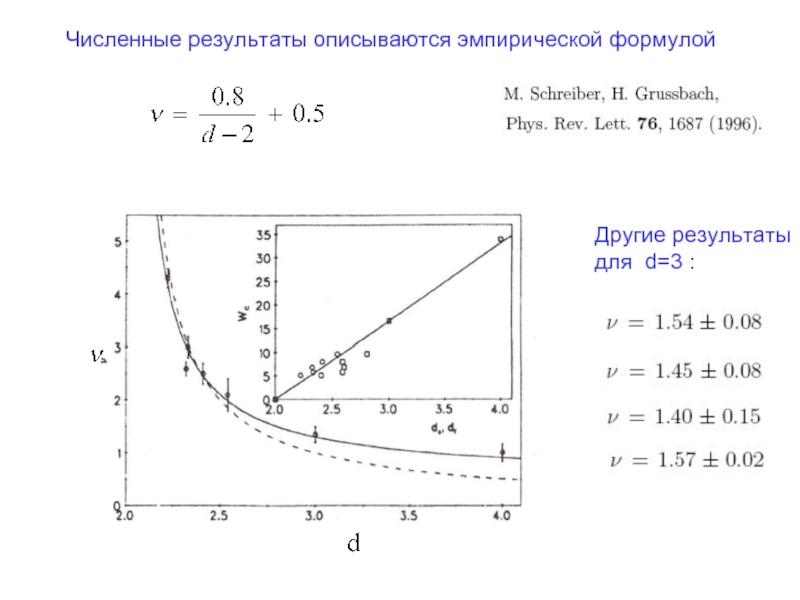
- 6. Численные результаты описываются эмпирической формулой Другие результаты для d=3 :
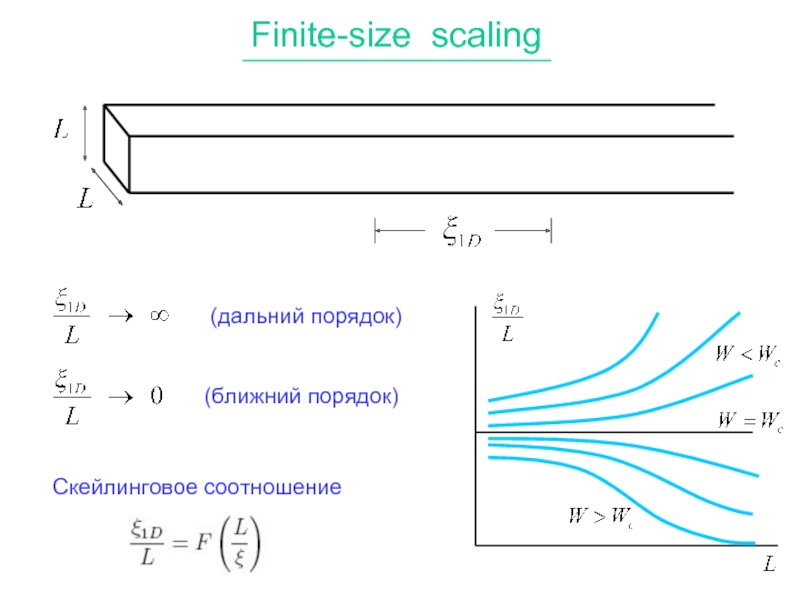
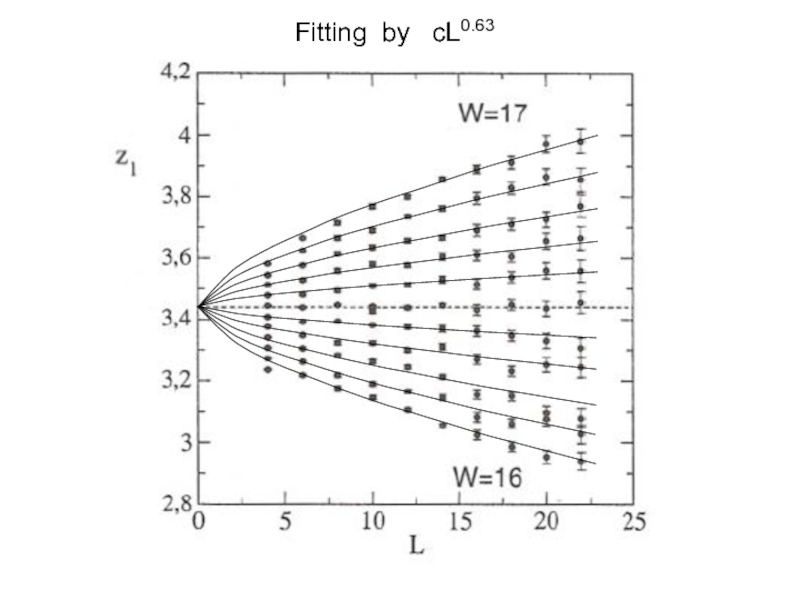
- 7. Finite-size
- 8. Теория Вольхардта-Вольфле Основана на существовании диффузионного
- 9. Уравнение самосогласования Базовый интеграл
- 10. Уравнение самосогласования Диэлектрическая фаза:
- 11. Квазиодномерные системы Для описания квазиодномерных систем базовый
- 12. Преобразование интегралов: что надо подставить в уравнение самосогласования
- 13. Уравнение самосогласования в
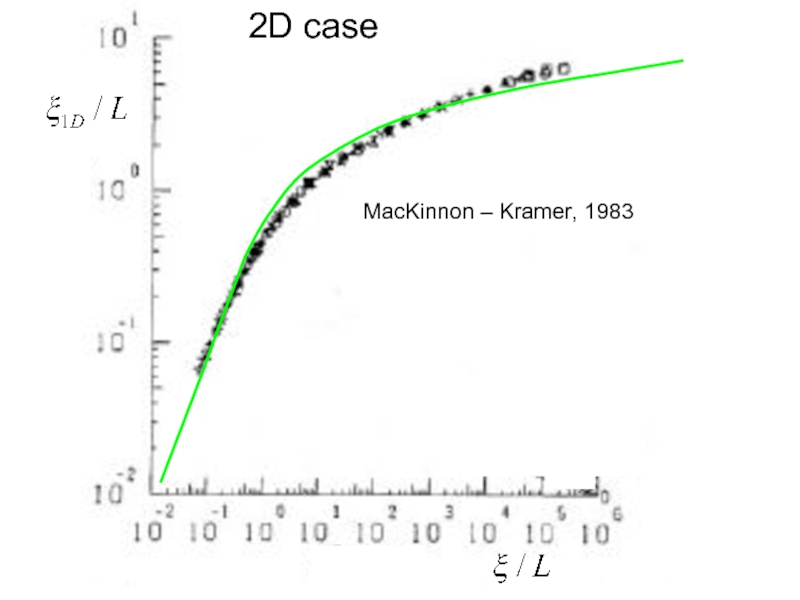
- 15. MacKinnon – Kramer, 1983 2D case
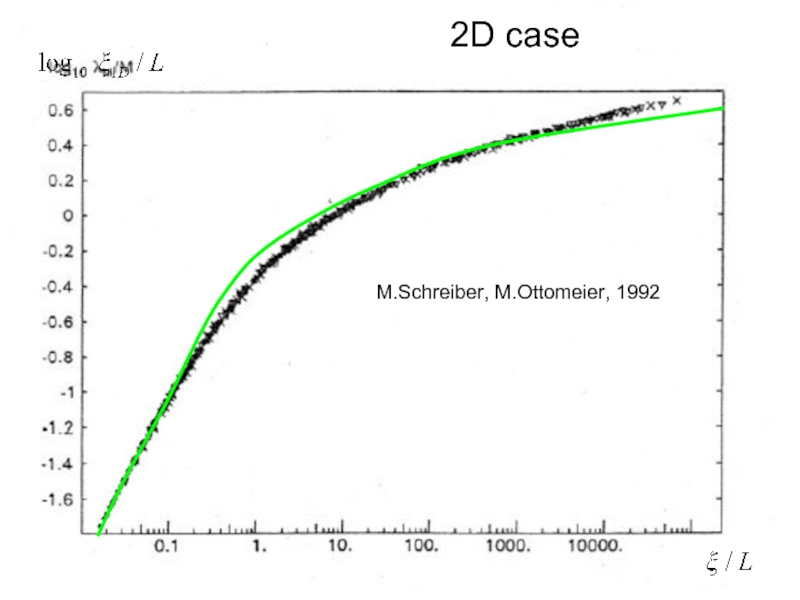
- 16. 2D case M.Schreiber, M.Ottomeier, 1992
- 17. Трехмерный случай Используя асимптотики
- 18. MacKinnon – Kramer, 1983 3D case
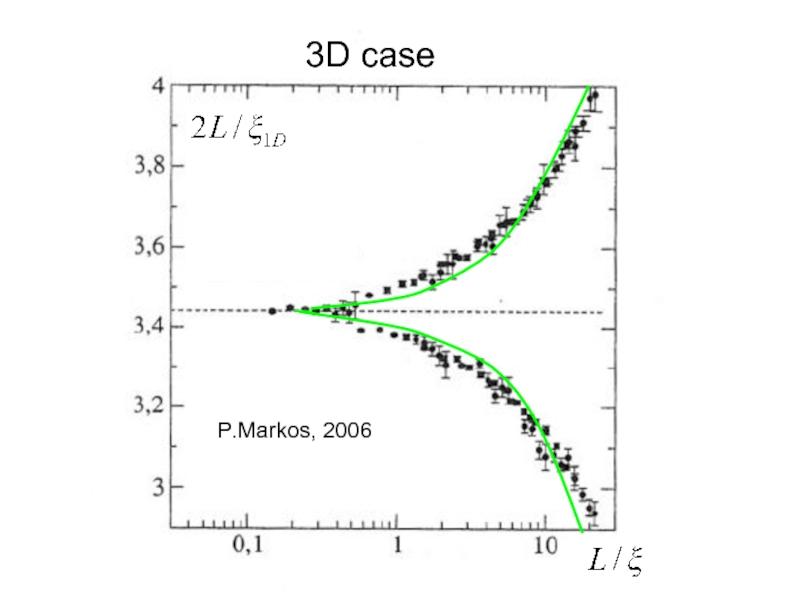
- 19. P.Markos, 2006 3D case
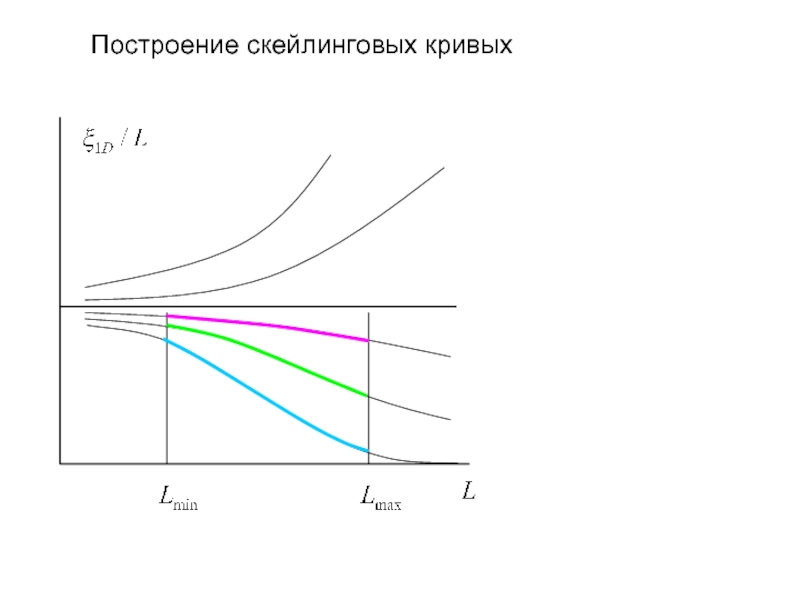
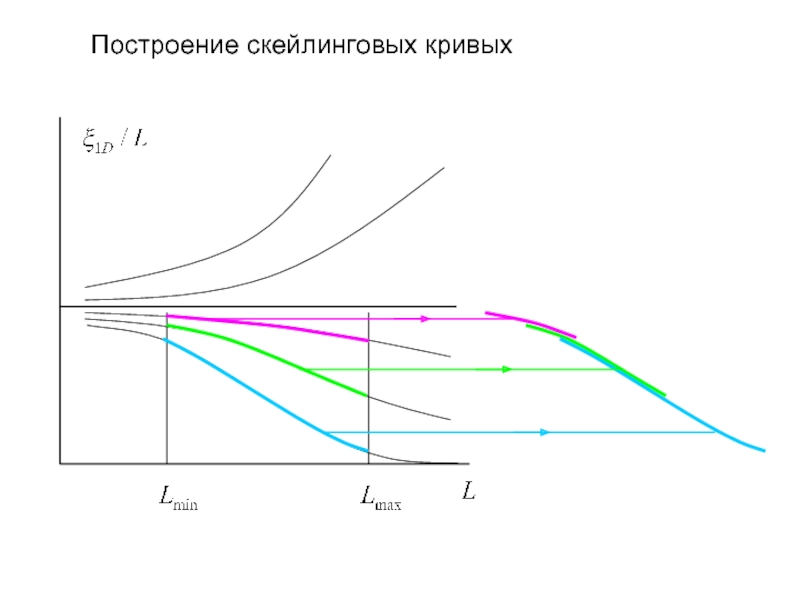
- 20. Построение скейлинговых кривых
- 21. Построение скейлинговых кривых
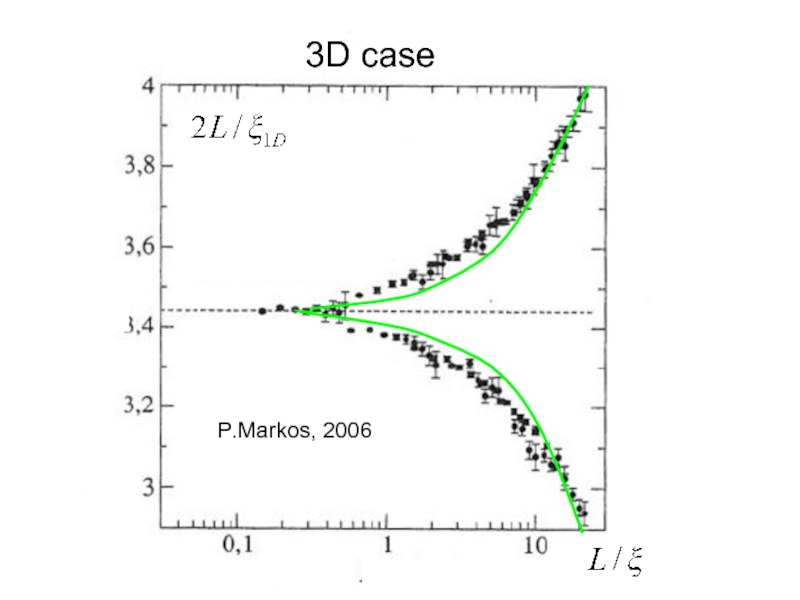
- 22. P.Markos, 2006 3D case
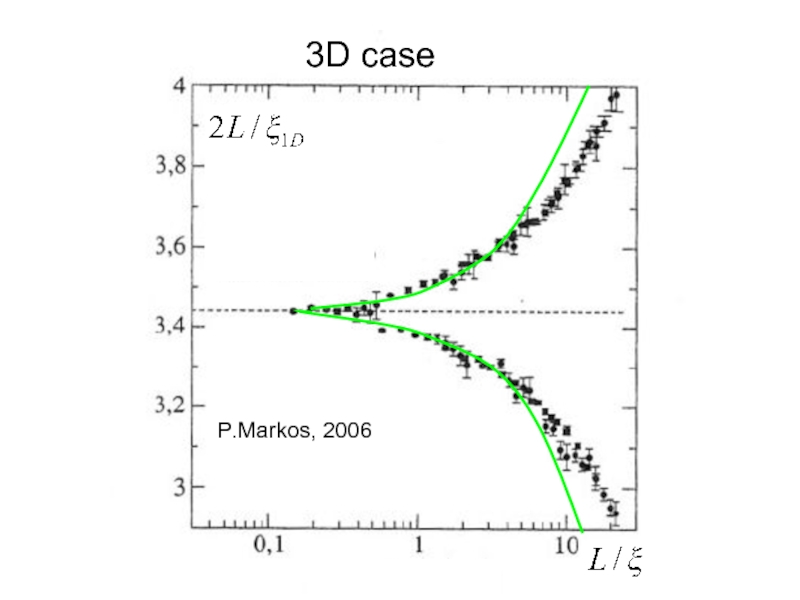
- 23. P.Markos, 2006 3D case
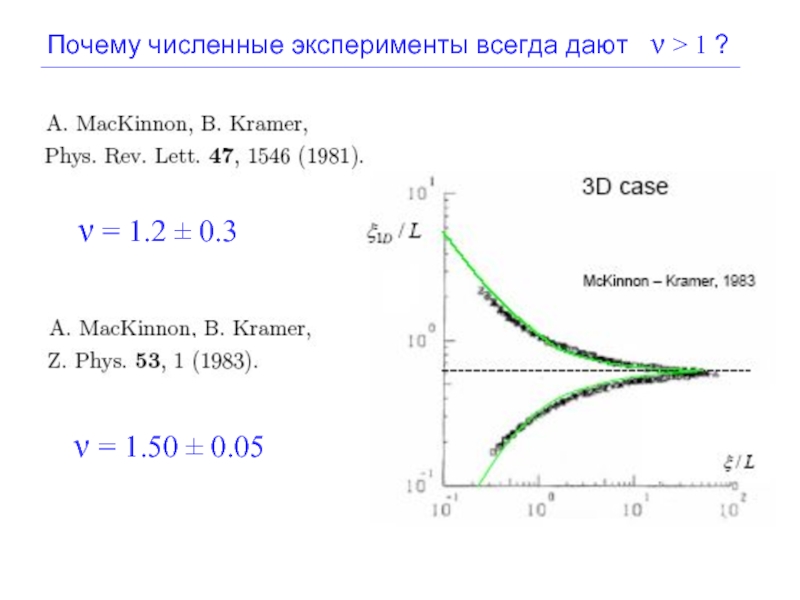
- 24. Почему численные эксперименты всегда дают ν
- 25. Ситуация в окрестности перехода Стандартные представления:
- 26. В теории Вольхардта – Вольфле при d=3
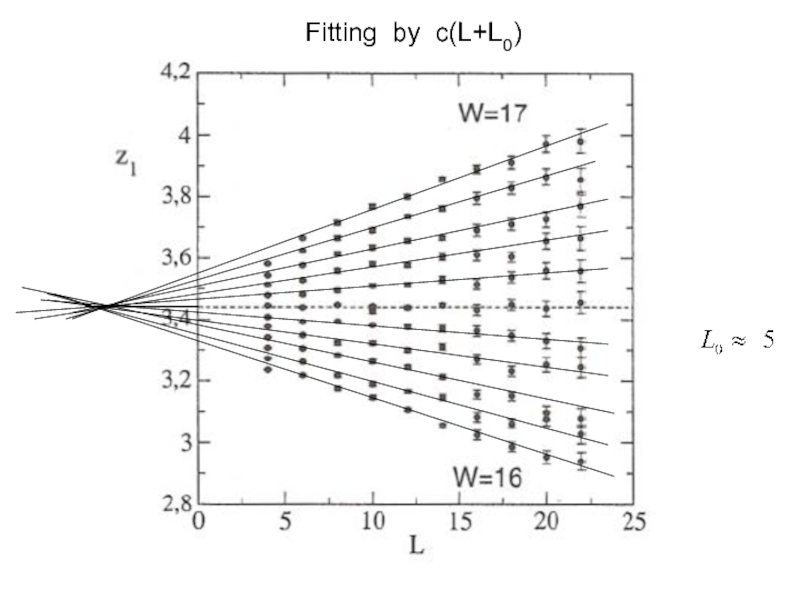
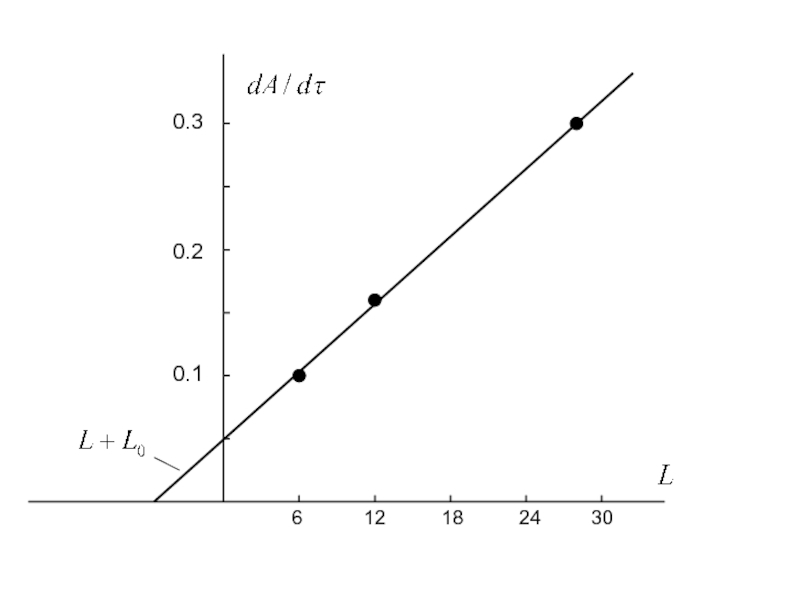
- 28. Fitting by c(L+L0)
- 29. Скейлинг для высших размерностей Меняется ситуация с
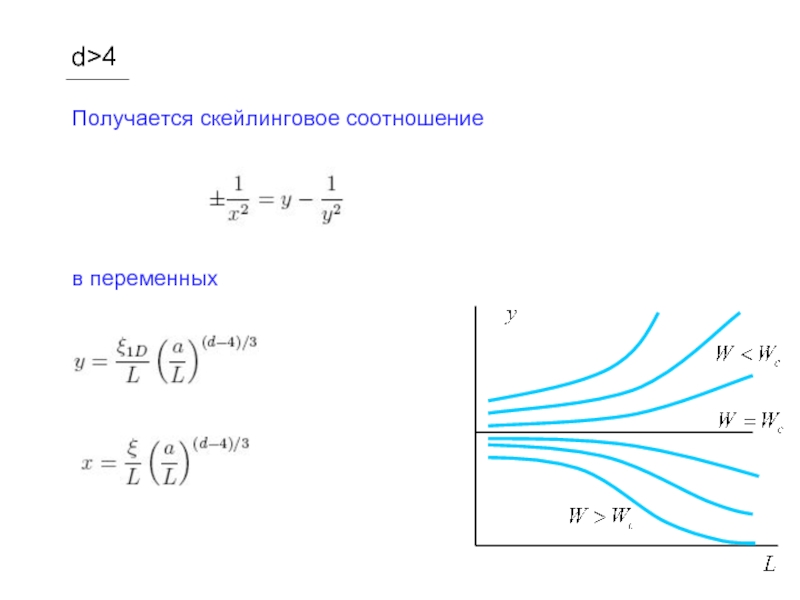
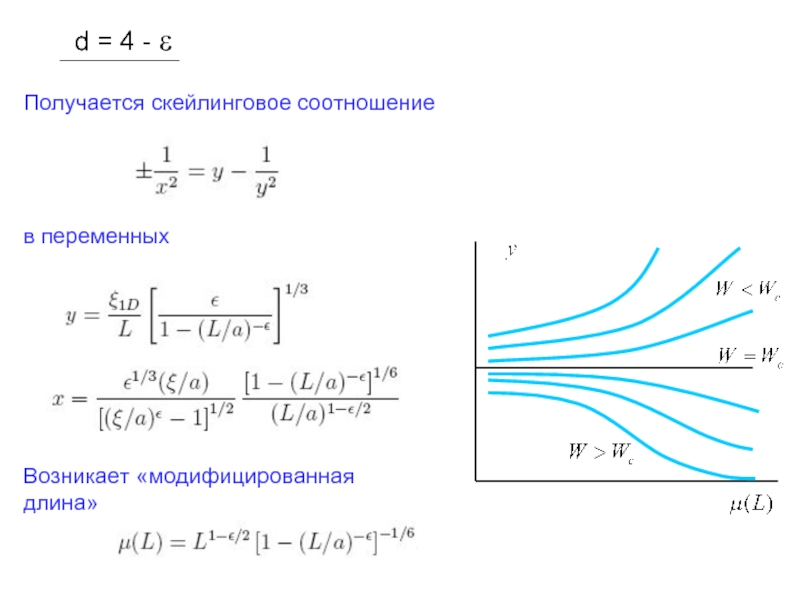
- 30. d>4 Получается скейлинговое соотношение
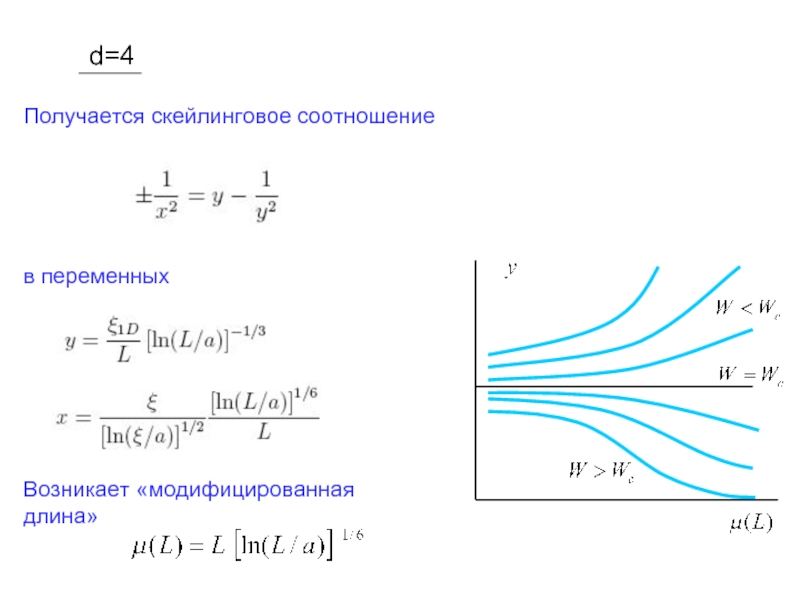
- 31. d=4
- 32. d = 4
- 33. Поведение в точке перехода для «стандартного» скейлингового параметра
- 34. Другие варианты конечно-размерного скейлинга Квазиодномерные
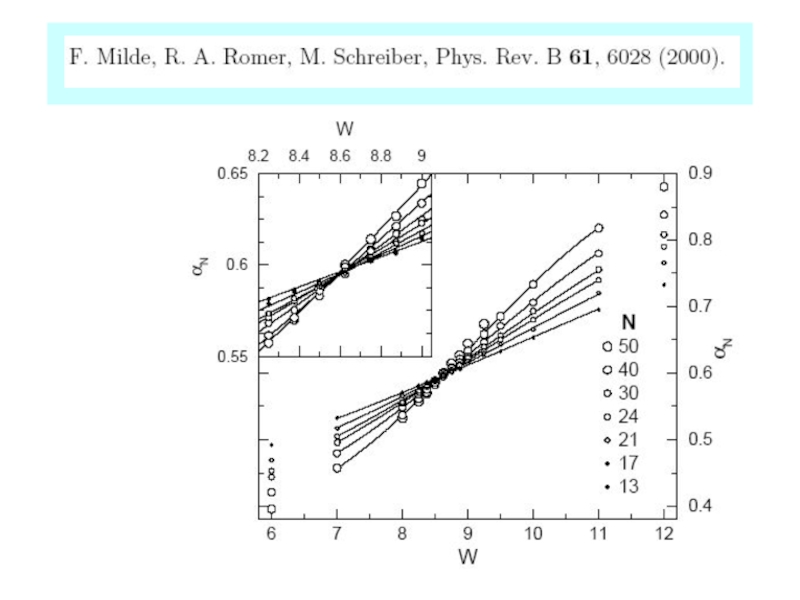
- 35. Статистика уровней I.Kh.Zharekeshev, B.Kramer, PRL,
- 36. 0.1 0.2 0.3 6
- 37. 0.1 0.2 0.3 6
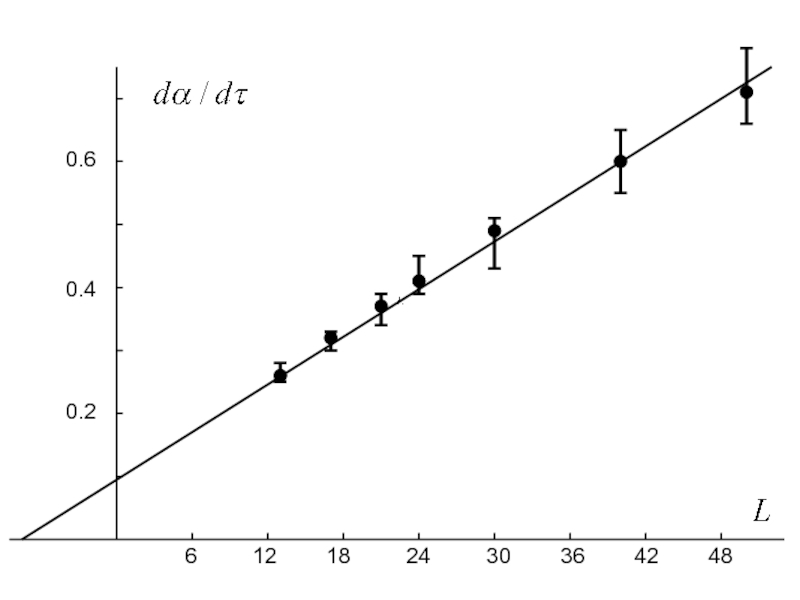
- 39. 0.2 0.4 0.6 6
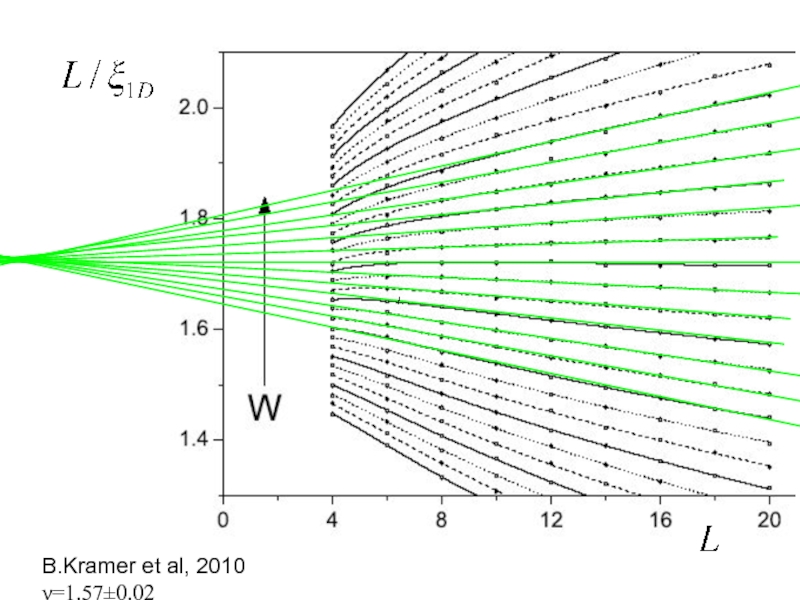
- 40. B.Kramer et al, 2010 ν=1.57±0.02
Переход Андерсона
Слайд 1
Переход Андерсона:
теория и численный эксперимент
И.М.Суслов
Институт физических проблем им. П.Л.Капицы РАН
Слайд 3Современная ситуация:
Численный счет противоречит всей прочей
информации о критическом поведении
Numerical analysis
of the Anderson localization
Слайд 4 Самосогласованная теория Вольхардта-Вольфле дает результат
который:
(а) выделяет значения dc1=2 и dc2=4
как верхнюю и нижнюю
критические размерности;
(б) согласуется с результатом для d=2+ε
(в) удовлетворяет скейлинговому соотношению s=ν(d-2) для d(г) дает независящие от d индексы для d>dc2;
(д) согласуется с результатами s=1 и ν=1/2 для d=∞.
(е) согласуется с экспериментальными результатами
s≈1 и ν≈1 для d=3.
критические размерности;
(б) согласуется с результатом для d=2+ε
(в) удовлетворяет скейлинговому соотношению s=ν(d-2) для d
(д) согласуется с результатами s=1 и ν=1/2 для d=∞.
(е) согласуется с экспериментальными результатами
s≈1 и ν≈1 для d=3.
Слайд 5
Гипотеза о том, что результаты теории Вольхардта-Вольфле
являются точными:
Вывод без грубых аппроксимаций:
Слайд 8Теория Вольхардта-Вольфле
Основана на существовании
диффузионного полюса
в неприводимой
четыреххвостке
играющей роль вероятности перехода
в квантовом кинетическом
уравнении.
Аппроксимация типа τ - приближения дает
уравнение самосогласования
уравнении.
Аппроксимация типа τ - приближения дает
уравнение самосогласования
= + +
= + +
Слайд 9Уравнение самосогласования
Базовый интеграл
конечен при m=0 только для d>2.
Металлическая фаза:
D=const при ω→ 0
т.е. s=1.
т.е. s=1.
Слайд 11Квазиодномерные системы
Для описания квазиодномерных систем базовый интеграл
достаточно представить в виде
( ) :
Член с расходится при m → 0 .
Разбиение интеграла
Член с расходится при m → 0 .
Разбиение интеграла
Слайд 13Уравнение самосогласования
в пределе a→0 дает скейлинговые соотношения
Определение функции H(z):
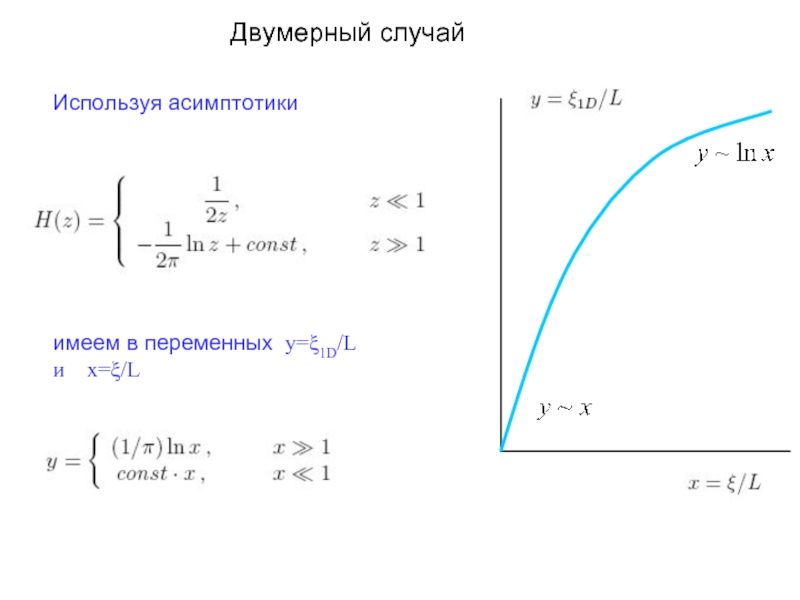
Слайд 17 Трехмерный случай
Используя асимптотики
имеем в переменных y=ξ1D/L и x=ξ/L
или для зависимостей от L
Слайд 26В теории Вольхардта – Вольфле при d=3 :
(с точностью до членов,
исчезающих при L → ∞ ).
Вместо стандартного
Вместо стандартного
P.Markos, 2006
Слайд 29Скейлинг для высших размерностей
Меняется ситуация с интегралом
Теперь нельзя устремлять Λ →
∞, но зато есть сходимость на
нижнем пределе
так что вычисление возможно аналитически при произвольных
значениях mL .
нижнем пределе
так что вычисление возможно аналитически при произвольных
значениях mL .
Слайд 34 Другие варианты конечно-размерного скейлинга
Квазиодномерные системы
Статистика уровней
Распределение кондактансов
Средний кондактанс
Параметр Таулеса
(«ускорение уровней»)
Inverse participation ratios
Inverse participation ratios
Слайд 35Статистика уровней
I.Kh.Zharekeshev, B.Kramer,
PRL, 79, 717 (1997)
Размеры до 1003
I.M.Suslov,
cond-mat/0105325
