- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Параболоиды презентация
Содержание
- 1. Параболоиды
- 2. Определение эллиптического параболоида Эллиптическим параболоидом называется поверхность
- 3. Если рассмотреть сечение эллиптического параболоида координатными плоскостями
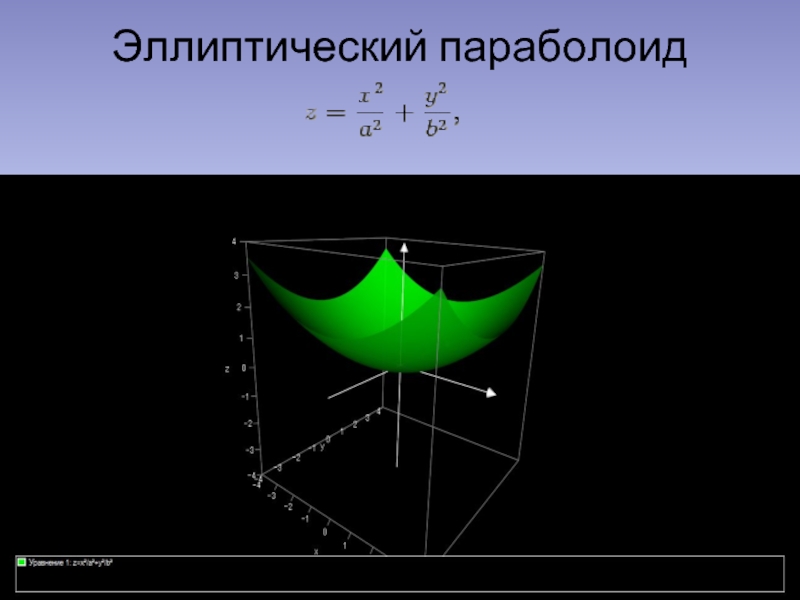
- 4. Эллиптический параболоид
- 5. Эллиптический параболоид
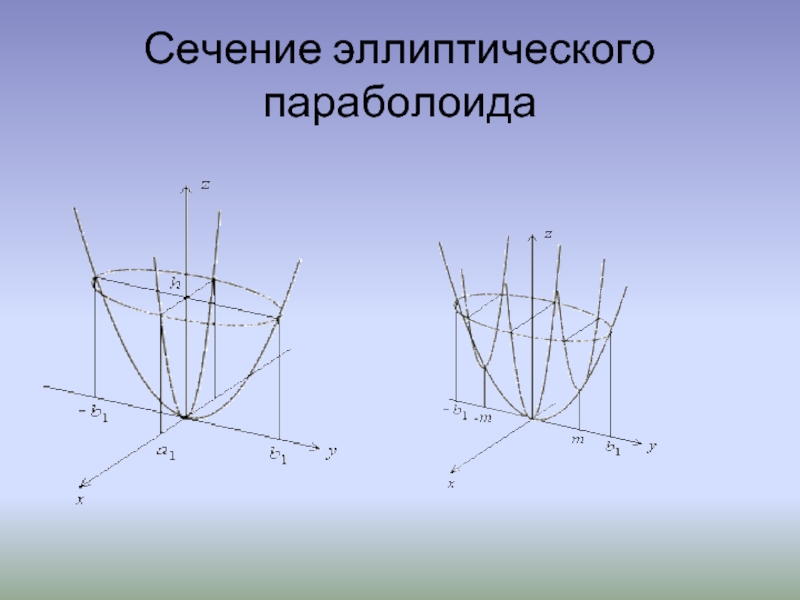
- 6. Сечение эллиптического параболоида
- 7. Определение гиперболического параболоида Гиперболическим параболоидом называется поверхность
- 8. Рассматривая аналогично сечения гиперболического параболоида плоскостью xOy:
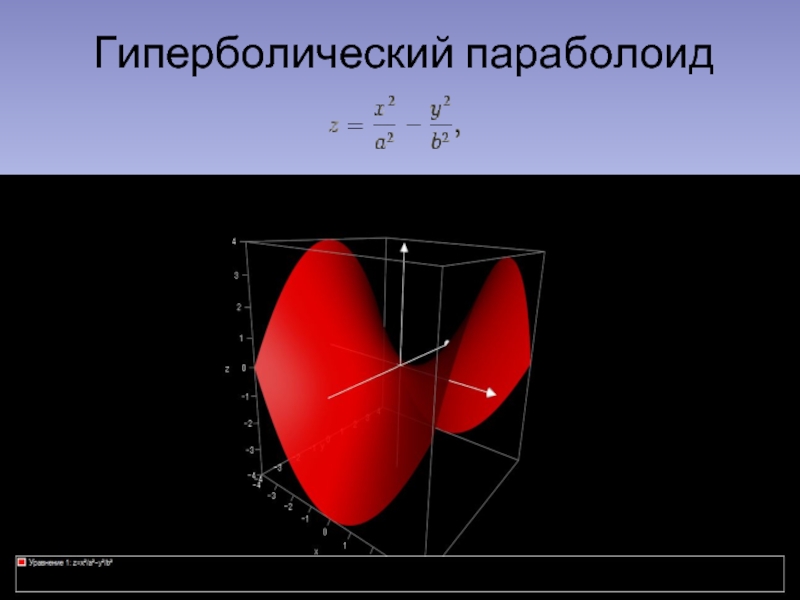
- 9. Гиперболический параболоид
- 10. Гиперболический параболоид
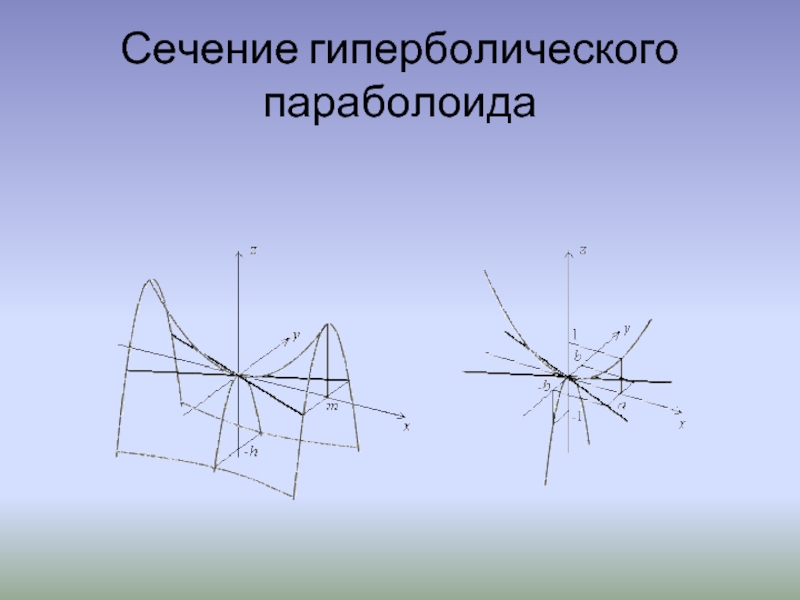
- 11. Сечение гиперболического параболоида
Слайд 1Параболоиды
Учитель математики ГОУ СОШ №718
Бугрова Елена Владимировна
(Использована программа АвтоГраф 3.20)
Слайд 2Определение эллиптического параболоида
Эллиптическим параболоидом называется поверхность второго порядка, которая в канонической
Ось аппликат Oz канонической системы координат является единственной осью симметрии эллиптического параболоида, плоскости xOz и yOz − плоскостями симметрии. Ось аппликат, называемая осью эллиптического параболоида, пересекает его в начале координат, эта точка называется вершиной параболоида.
Слайд 3Если рассмотреть сечение эллиптического параболоида координатными плоскостями xOz: y = 0
откуда при подстановке второго уравнения в первое последовательно получаем:
и уравнение параболы
.
Получаемые таким образом параболы лежат в параллельных плоскостях, отличаясь лишь положением в пространстве.
Рассматривая аналогично сечения эллиптического параболоида плоскостью xOy: z = 0, а также плоскостями, параллельными плоскости xOy: z = h, получаем кривые второго порядка эллиптического типа. Это – либо эллипс (при h > 0), либо пара мнимых пересекающихся прямых, т.е. точка (при h = 0), либо мнимый эллипс (при h < 0).
Слайд 7Определение гиперболического параболоида
Гиперболическим параболоидом называется поверхность второго порядка, которая в канонической
Ось аппликат Oz канонической системы координат является единственной осью симметрии гиперболического параболоида, плоскости xOz и yOz − плоскостями симметрии. Ось аппликат, называемая осью гиперболического параболоида, пересекает его в начале координат; эта точка называется вершиной параболоида.
Слайд 8Рассматривая аналогично сечения гиперболического параболоида плоскостью xOy: z = 0, а
Если рассмотреть сечение гиперболического параболоида координатными плоскостями xOz: y = 0 и yOz: x = 0, и плоскостями, им параллельными (x = h1, y = h2), то в сечении получаются параболы. Например, сечение гиперболического параболоида плоскостью x = h1 задается системой уравнений
откуда при подстановке второго уравнения в первое последовательно получаем:
и уравнение параболы
.