- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
П И Ф А Г О Р презентация
Содержание
Слайд 1П И Ф А Г О Р
Древнегреческий философ и
Слайд 2История открытия теоремы
Обычно открытие теоремы Пифагора приписывают древнегреческому философу и математику
Но несмотря на все эти доказательства, имя Пифагора столь прочно сплавилось с теоремой Пифагора, что сейчас просто невозможно представить, что это словосочетание распадётся.
Слайд 3Способы
доказательства
теоремы
Пифагора
Да, путь познания не гладок.
Но знайте
Слайд 4
А
В
С
А
В
С
Простейшее доказательство
Достаточно взглянуть на мозаику из цветных треугольников
Слайд 5
С2
b2
a2
а
а
а
а
а
а
а
а
b
b
b
b
b
b
b
b
c
c
c
c
c
c
Равновеликость фигур
На рисунке изображено два равных квадрата. Длина сторон каждого квадрата равна а+b. Каждый из квадратов разбит на части, состоящие из квадратов и прямоугольных треугольников. Ясно, что если от площади квадрата отнять учетверенную площадь прямоугольного треугольника с катетами а, b., то остаются равные площади, т.е. с2 = а2 + b2.
Слайд 6
1
2
A
B
C
D
E
F
P
N
M
Q
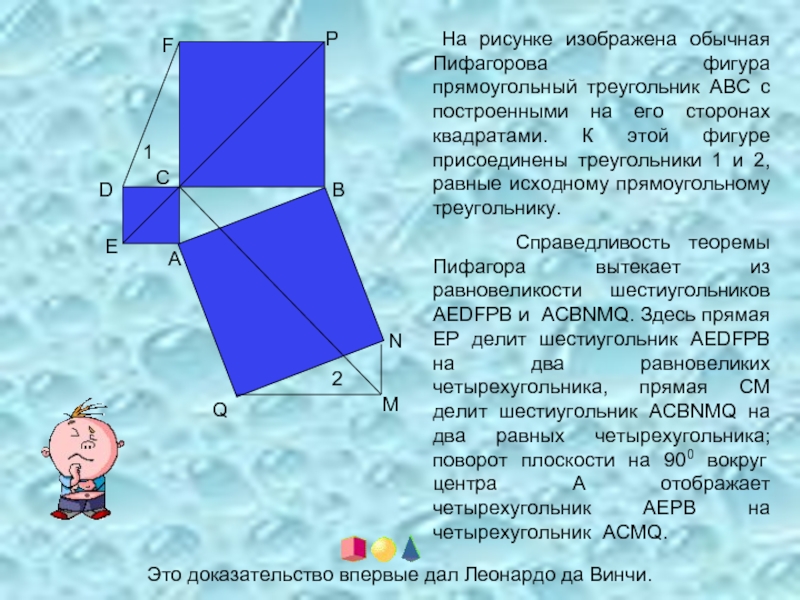
На рисунке изображена обычная Пифагорова фигура прямоугольный треугольник АВС с
Справедливость теоремы Пифагора вытекает из равновеликости шестиугольников AEDFPB и ACBNMQ. Здесь прямая ЕР делит шестиугольник AEDFPB на два равновеликих четырехугольника, прямая СМ делит шестиугольник ACBNMQ на два равных четырехугольника; поворот плоскости на 900 вокруг центра А отображает четырехугольник AEPB на четырехугольник ACMQ.
Это доказательство впервые дал Леонардо да Винчи.
Слайд 7А
В
С
D
F
E
a
b
c
Оригинальное доказательство, предложенное Гофманом. Здесь треугольник АВС с прямым углом С;
Слайд 8
с
с
с
с
½ab
½ab
½ab
½ab
(b-a)2
A
B
C
b
a
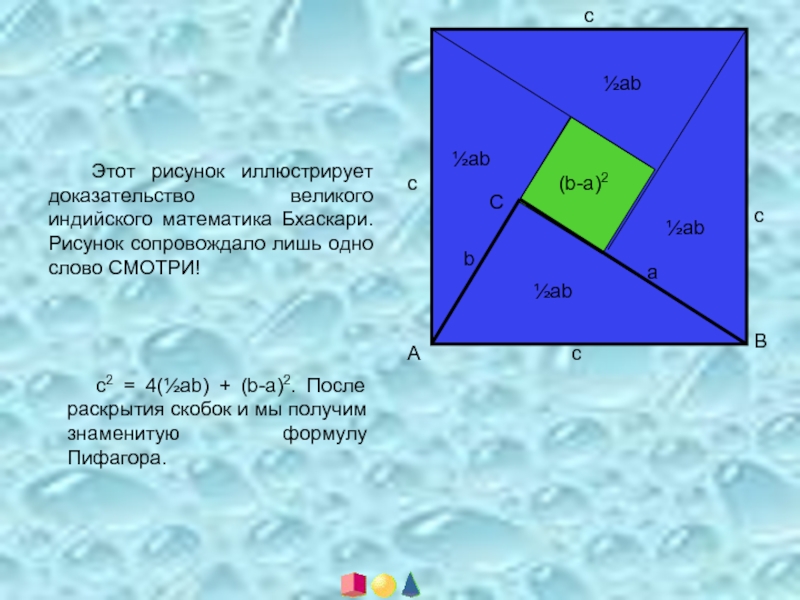
Этот рисунок иллюстрирует доказательство великого индийского математика Бхаскари. Рисунок
с2 = 4(½аb) + (b-a)2. После раскрытия скобок и мы получим знаменитую формулу Пифагора.
Слайд 9А
С
В
h
M
b1
a1
a
b
Приведем в современном изложении одно из доказательств, принадлежащих Пифагору.
На рисунке треугольник АВС – прямоугольный, С – прямой угол, (СМ ┴ АВ) b1 - проекция катета b на гипотенузу, a1 – проекция катета на гипотенузу, h – высота треугольника, проведенная к гипотенузе.
Из того что треугольник ∆АВС подобен ∆АСМ, следует b2 = сb1; из того что ∆АВС подобен ∆ВСМ следует а2 = са1. Складывая почленно равенства, получим а2 + b2 = сb1 + са1 = с(b1 + а1) = с2.
Если Пифагор действительно предложил такое доказательство, то он был знаком и с целым рядом важных геометрических теорем, которые современные историки математики обычно приписывают Евклиду.
Слайд 10
А
В
С
а
с
b
Доказательство Мёльманна
Площадь данного прямоугольного треугольника, с одной стороны, равна
Слайд 11а
а
с
с
b
b
Доказательство Гарфилда
На рисунке три прямоугольных треугольника составляют трапецию.
Слайд 12
с2
а
b
а2
b2
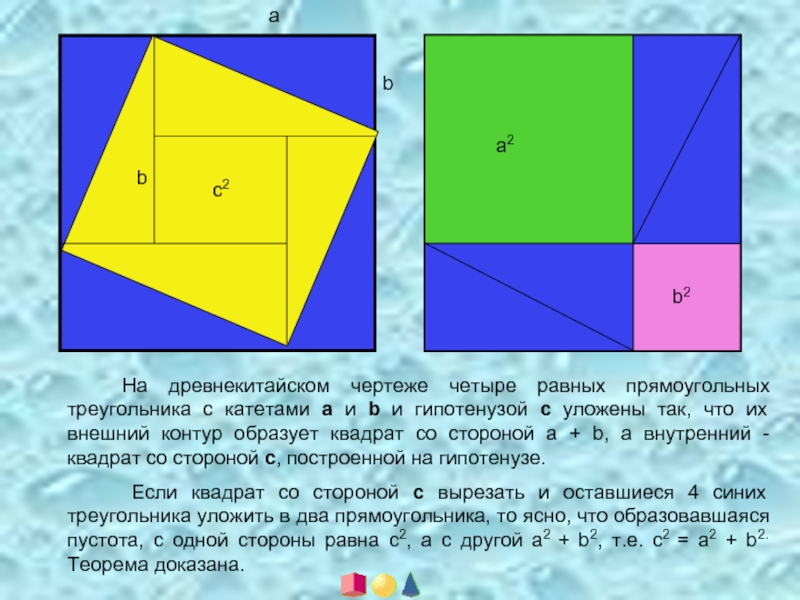
На древнекитайском чертеже четыре равных прямоугольных треугольника с катетами
Если квадрат со стороной с вырезать и оставшиеся 4 синих треугольника уложить в два прямоугольника, то ясно, что образовавшаяся пустота, с одной стороны равна с2, а с другой а2 + b2, т.е. с2 = а2 + b2. Теорема доказана.
b