начальных классов МАОУ СОШ № 2 Тертица И. Б.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Особенности обучения учащихся младшего школьного возраста решению нестандартных (олимпиадных) задач презентация
Содержание
- 1. Особенности обучения учащихся младшего школьного возраста решению нестандартных (олимпиадных) задач
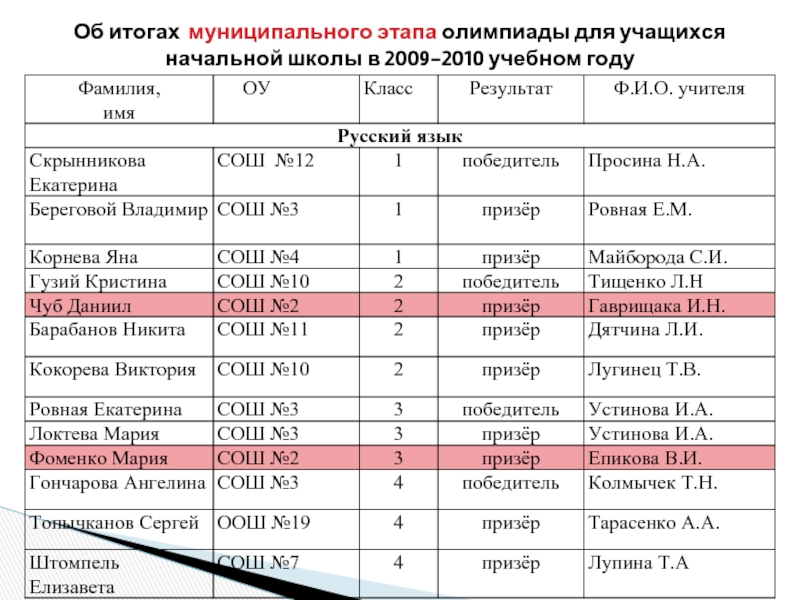
- 2. Об итогах муниципального этапа олимпиады для учащихся
- 3. Об итогах муниципального этапа олимпиады для учащихся начальной школы в 2009-2010 учебном году
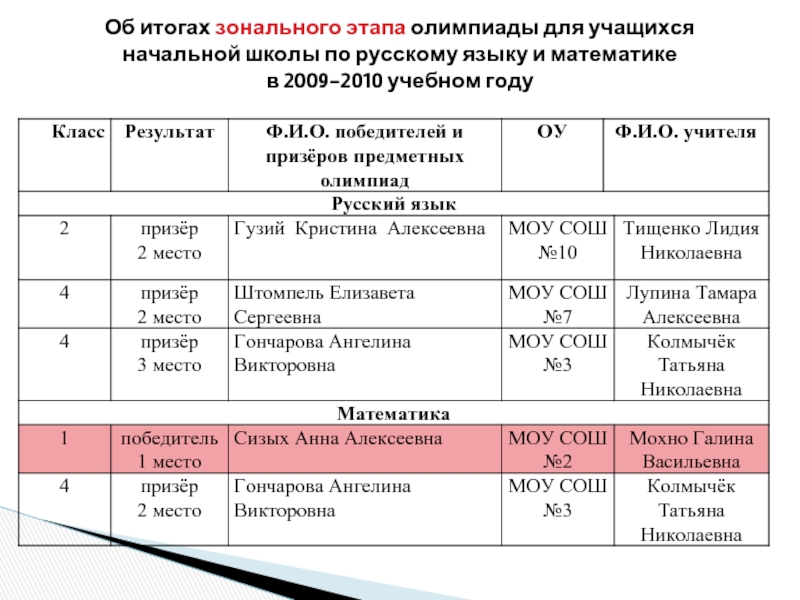
- 4. Об итогах зонального этапа олимпиады для учащихся
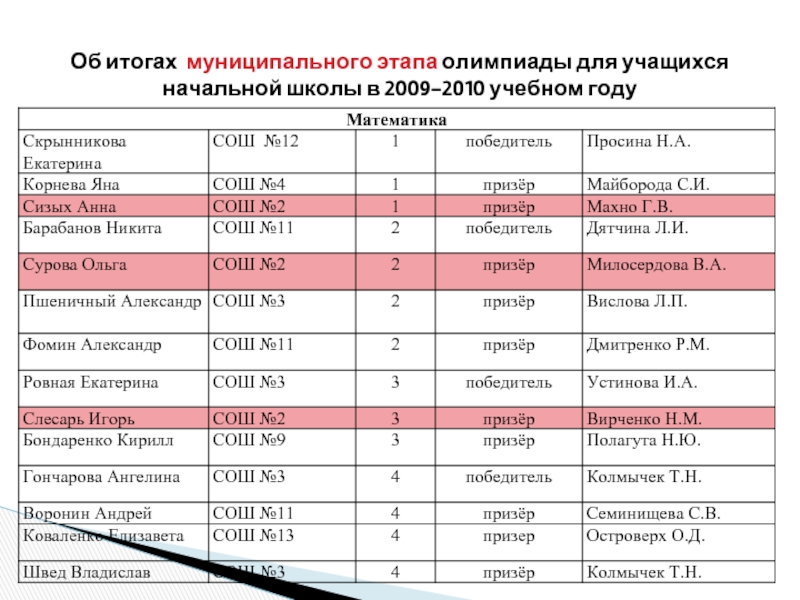
- 5. Об итогах муниципального этапа олимпиады для учащихся
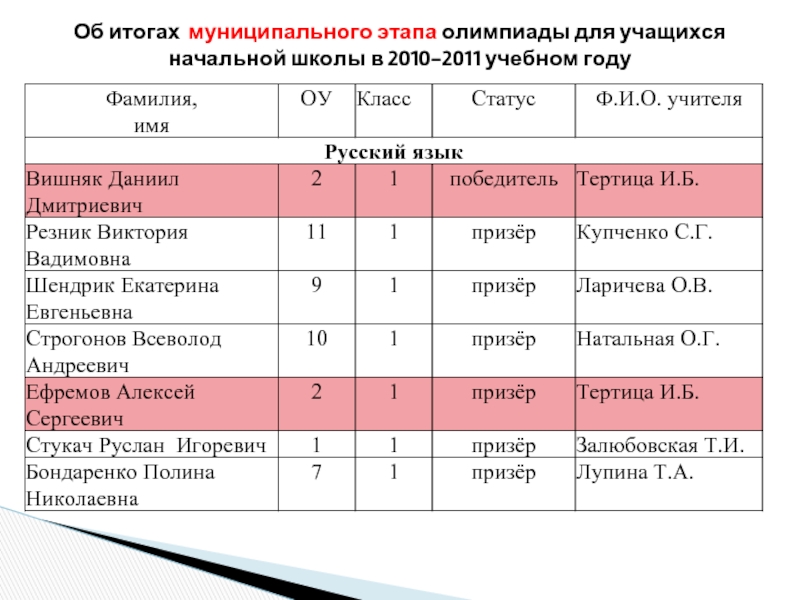
- 12. Участие в предметных олимпиадах муниципального уровня 2010- 2011 уч год
- 13. Об участии в зональном этапе олимпиады по
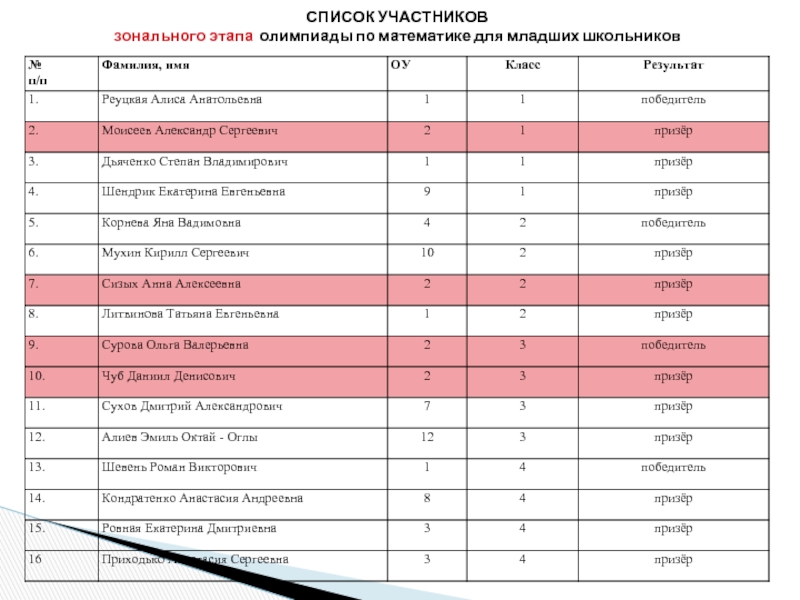
- 14. СПИСОК УЧАСТНИКОВ зонального этапа олимпиады по математике для младших школьников
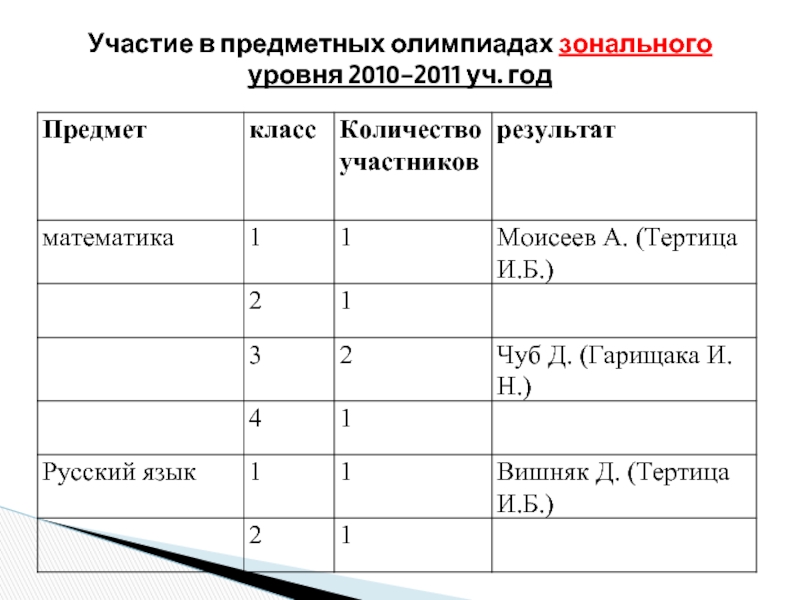
- 15. Участие в предметных олимпиадах зонального уровня 2010-2011 уч. год
- 16. Одаренный ребенок –
- 17. Виды одаренности «актуальная» - очевидная, замеченная психологами,
- 18. Две крайние точки зрения: все дети
- 19. Диагностика 1.Обученность 2.Обучаемость 3.Интерес к предмету
- 20. «Школа 2100» – ориентир на личность, формирование ученика как самостоятельно мыслящего человека
- 21. Под «нестандартной задачей» мы понимаем задачу, заключающую
- 22. Вывод: обучение решению нестандартных (олимпиадных) задач должно
- 23. Аппарат творчества Психологические свойства личности, обстоятельства, настрои
- 24. кризисный Стремление к успеху, эксперименту Отсутствие опыта
- 25. Схема подготовки учащихся Детей стабильного возраста
- 26. Признаки ( развитое воображение, критичность мышления, аналитичность,
- 27. Формирование и развитие умений творческой самостоятельной работы
- 28. Сначала выделяется суть проблемы. Происходит ориентация в
- 29. « Ответственность преподавателей математики особенно велика, так
- 30. Особенности логического мышления младших школьников.
- 31. От мышления наглядно-образного К словесно-логическому, понятийному мышлению
- 32. При общении в начальных классах у детей
- 33. Все операции логического мышления тесно взаимосвязаны и
- 34. Дидактические игры стимулируют прежде всего наглядно –
- 35. ВИДЫ нестандартных задач
- 37. 1-й подтип. Какое из чисел 333, 555,
- 38. 1. Тройка лошадей проскакала 15 км. Сколько
- 39. 1. Три спички выложены на столе так,
- 40. Способы решения нестандартных задач
- 41. 1. Коротышки из цветочного городка посадили арбуз.
- 42. Вадим, Сергей и Михаил изучают различные иностранные
- 43. Подготовительная группа: Учим выделять существенные признаки
- 44. Для детей со средним и низким уровнем
- 45. Решение нестандартных задач формирует у учащихся умения
- 46. Сухомлинский наблюдал за ходом мышления детей, и
Об итогах муниципального этапа олимпиады для учащихся
начальной школы в 2009-2010 учебном году
Слайд 1Особенности обучения учащихся младшего школьного возраста решению нестандартных (олимпиадных) задач
Подготовила:
учитель
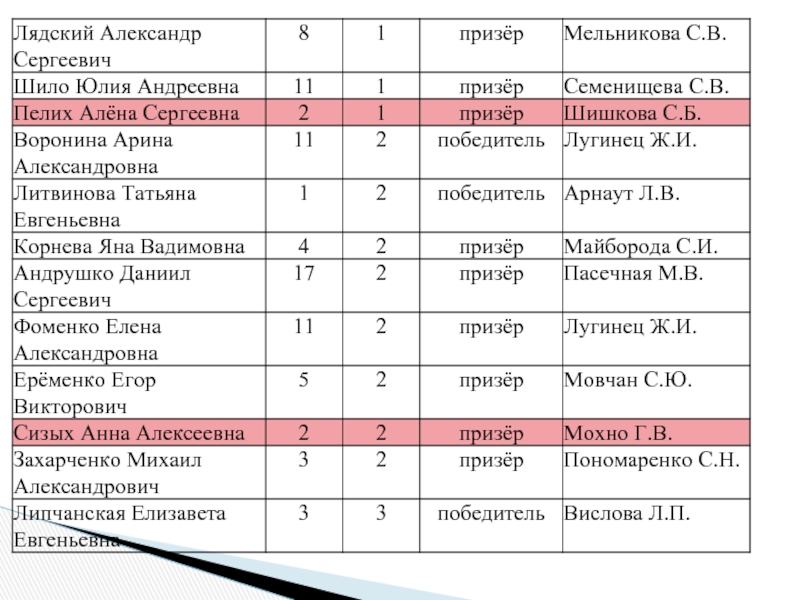
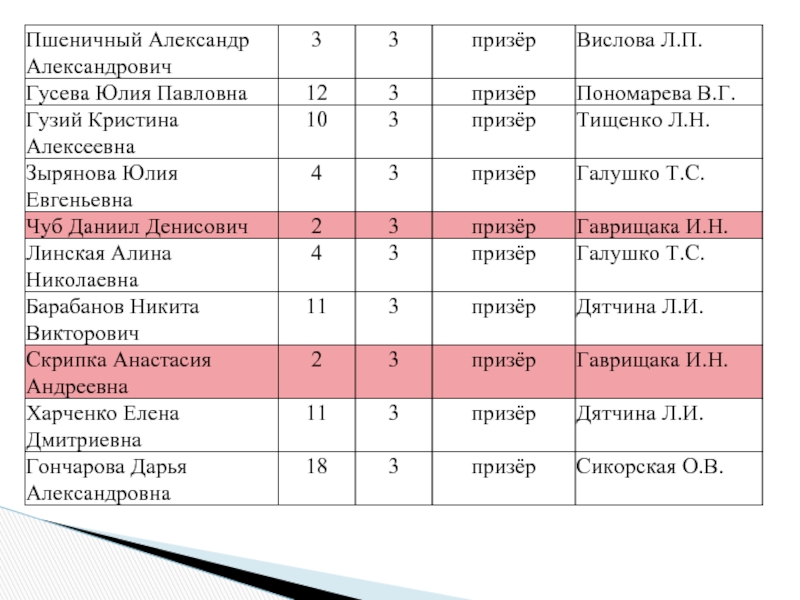
Слайд 2Об итогах муниципального этапа олимпиады для учащихся начальной школы в 2009-2010
учебном году
Слайд 3Об итогах муниципального этапа олимпиады для учащихся начальной школы в 2009-2010
учебном году
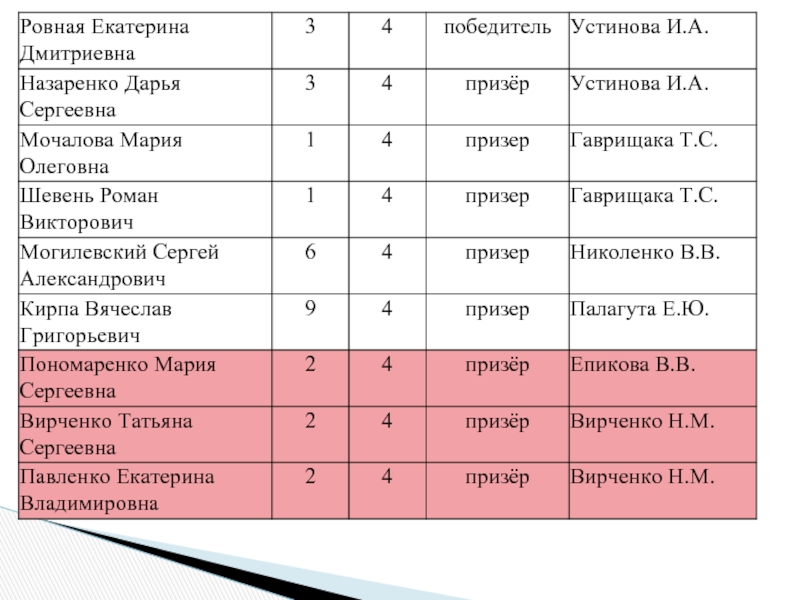
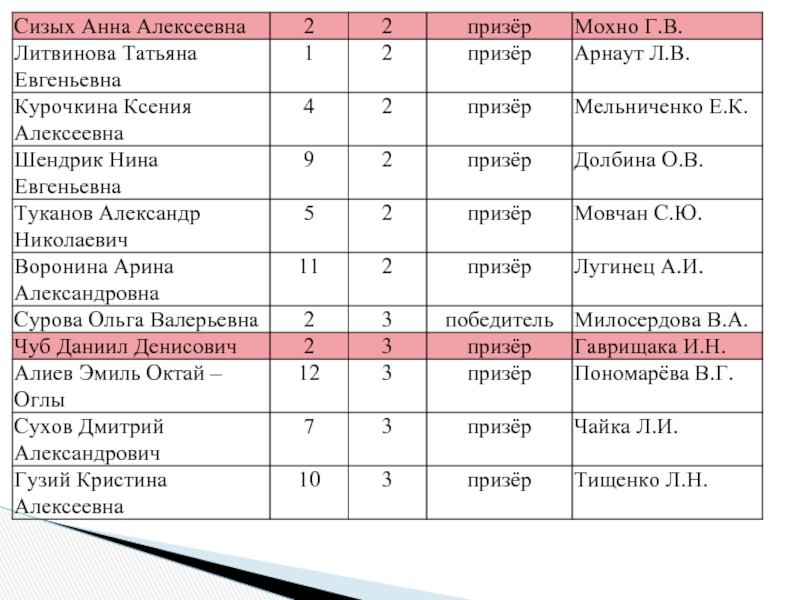
Слайд 4Об итогах зонального этапа олимпиады для учащихся начальной школы по русскому
языку и математике
в 2009-2010 учебном году
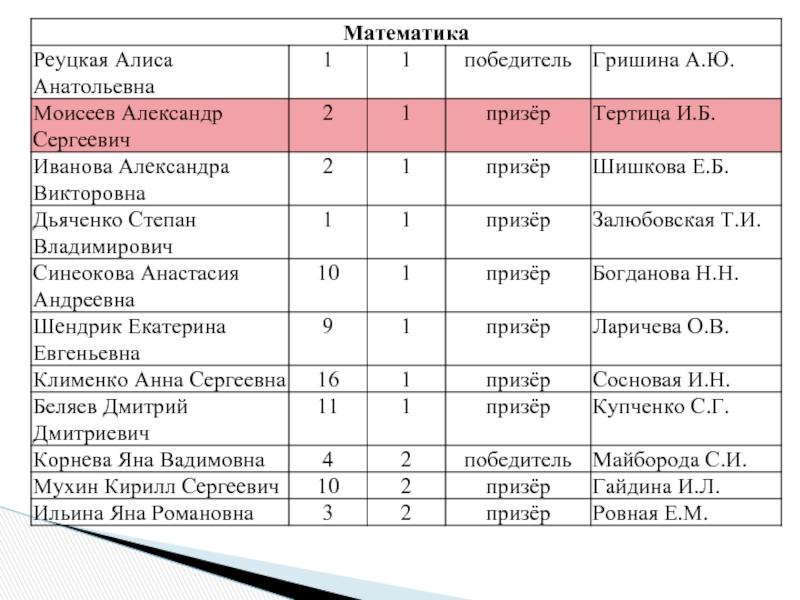
Слайд 5Об итогах муниципального этапа олимпиады для учащихся начальной школы в 2010-2011
учебном году
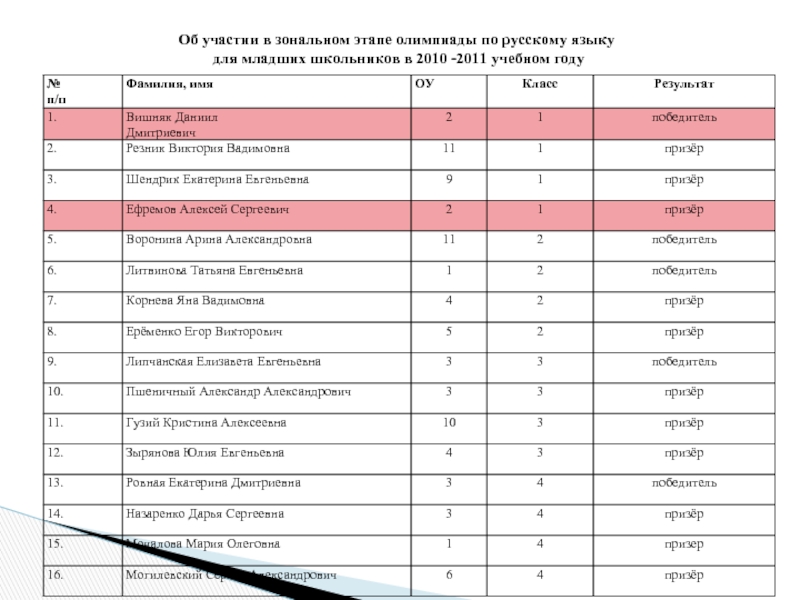
Слайд 13Об участии в зональном этапе олимпиады по русскому языку
для младших
школьников в 2010 -2011 учебном году
Слайд 16 Одаренный ребенок – это ребенок, который выделяется яркими, очевидными, иногда выдающимися
достижениями
(или имеет внутренние предпосылки для таких достижений)
Одаренность - постоянно развивающийся потенциал, существующий только в динамике, а потому практически непрерывно меняющийся.
Детство - самый благодатный период для развития одаренности.
Слайд 17Виды одаренности
«актуальная» - очевидная, замеченная психологами, педагогами, родителями
«потенциальная», которая не
сразу заметна, неочевидна для окружающих
Формы одаренности
интеллектуальная
творческая
Слайд 18Две крайние точки зрения:
все дети
являются одаренными
одаренные дети встречаются крайне редко
Слайд 20«Школа 2100» – ориентир на личность, формирование ученика как самостоятельно мыслящего
человека
Слайд 21Под «нестандартной задачей» мы понимаем задачу, заключающую в себе нечто оригинальное
творческое.
«Олимпиадная» задача трактуется как определённое задание из какой-либо области знаний, данное учащимся для соревнования.
Решение «олимпиадной» задачи – это творчество, определяющееся самим процессом.
«Олимпиадная» задача трактуется как определённое задание из какой-либо области знаний, данное учащимся для соревнования.
Решение «олимпиадной» задачи – это творчество, определяющееся самим процессом.
Для реализации этого творческого процесса учащийся должен овладеть аппаратом творческой деятельности.
Чем больше значимых элементов, составляющих процесс творчество, задействовано, тем быстрее будет достигнута цель
Слайд 22Вывод: обучение решению нестандартных (олимпиадных) задач должно вестись с учётом внутри
возрастного разграничения внутри него кризисного и стабильного возраста.
Кризисный возраст: ученики 1-2 классов более перспективны для овладения основ творческой деятельности
Стабильный возраст: 8-12 лет даёт возможность ученику приобрести научный тип мышления
Слайд 23Аппарат творчества
Психологические свойства личности, обстоятельства, настрои
Творческое мышление, умение творчески и самостоятельно
работать, научные знания
Слайд 24кризисный
Стремление к успеху, эксперименту
Отсутствие опыта
Неустойчивое внимание
Недостаточный уровень организованности, воли
стабильный
Стремительный темп усвоения
навыков
Проявление фантазии
Проявление самостоятельности
Ожидание тайн
Проявление фантазии
Проявление самостоятельности
Ожидание тайн
Слайд 25Схема подготовки учащихся
Детей стабильного возраста обучают в системе
Детей кризисного возраста обучают
этапам, компонентам, показывая их связь, ориентируясь на сравнение, обобщение, анализ
Слайд 26Признаки ( развитое воображение, критичность мышления, аналитичность, оригинальность )
Качества ( открытость
опыту, беглость мышления, широта категоризации)
Умения ( определять скрытый признак, анализировать, быстро переходить от одной категории к другой)
Умения ( определять скрытый признак, анализировать, быстро переходить от одной категории к другой)
ТВОРЧЕСКОЕ МЫШЛЕНИЕ
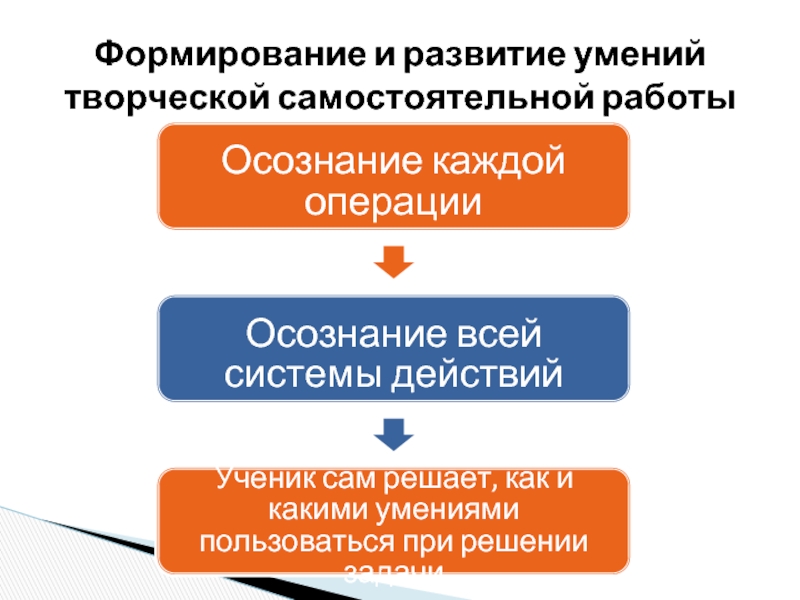
Слайд 27Формирование и развитие умений творческой самостоятельной работы
Осознание каждой операции
Осознание всей системы
действий
Ученик сам решает, как и какими умениями пользоваться при решении задачи
Слайд 28Сначала выделяется суть проблемы.
Происходит ориентация в знаниях: находятся нужные знания, пути
и способы решения задачи, привлекается опыт для выдвижения гипотезы.
Потом ставятся эксперименты и проводятся специальные наблюдения с последующим их обобщением в виде выводов и гипотез.
Затем оформляются результаты решения нестандартных задач в виде математических, графических, предметных структур.
Устанавливается социальная ценность полученного продукта.
Потом ставятся эксперименты и проводятся специальные наблюдения с последующим их обобщением в виде выводов и гипотез.
Затем оформляются результаты решения нестандартных задач в виде математических, графических, предметных структур.
Устанавливается социальная ценность полученного продукта.
Схема творческой деятельности при решении нестандартных задач
Слайд 29« Ответственность преподавателей математики особенно велика, так как отдельного предмета «логика»
в школе нет, и умение логически мыслить и строить правильные умозаключения необходимо развивать с первых «прикосновений» детей к математике. И то, как этот процесс мы сможем внедрить в различные школьные программы, будет зависеть какое поколение придёт нам на смену»
Г. Н. Дорофеев писал:
Слайд 30Особенности логического мышления младших школьников.
Предметно-действенное
(наглядно-действенное)
Наглядно-образное.
Абстрактное (словесно-логическое)
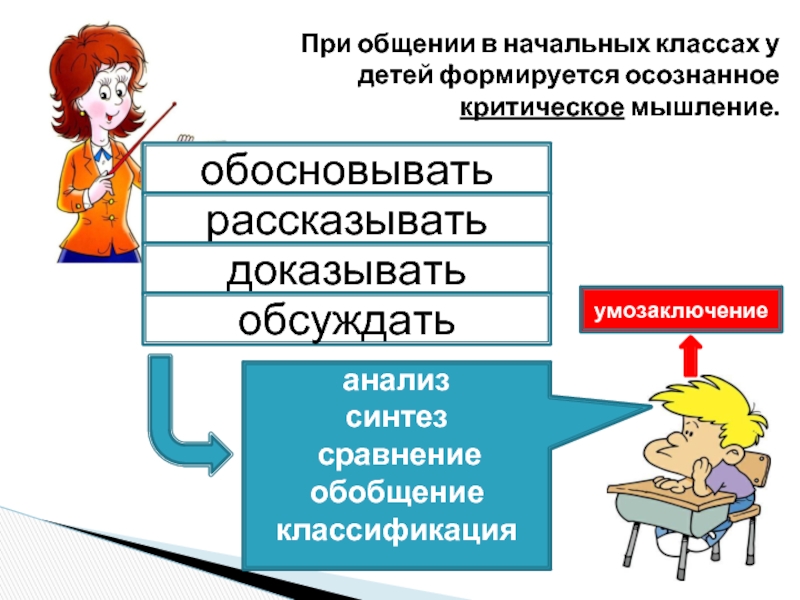
Слайд 32При общении в начальных классах у детей формируется осознанное критическое мышление.
обосновывать
рассказывать
доказывать
обсуждать
анализ
синтез
сравнение обобщение классификация
умозаключение
Слайд 33Все операции логического мышления тесно взаимосвязаны и их полноценное формирование возможно
только в комплексе.
Только взаимообусловленное их развитие способствует развитию логического мышления в целом.
Именно в младшем школьном возрасте необходимо проводить целенаправленную работу по обучению детей основным приёмам мыслительной деятельности.
Только взаимообусловленное их развитие способствует развитию логического мышления в целом.
Именно в младшем школьном возрасте необходимо проводить целенаправленную работу по обучению детей основным приёмам мыслительной деятельности.
Выводы:
Слайд 34Дидактические игры стимулируют прежде всего наглядно – образное мышление, а затем
и словесно – логическое.
Головоломки.
Нестандартные задачи.
Ребусы
Загадки, шарады, кроссворды
Головоломки.
Нестандартные задачи.
Ребусы
Загадки, шарады, кроссворды
Изучив теорию развития мышления и развитие творческой самостоятельности, я стала на уроках и во внеклассной работе по математике включать задания, связанные с умением делать выводы, используя приёмы анализа, синтеза, сравнения и обобщения.
Слайд 371-й подтип. Какое из чисел 333, 555, 666, 999 не делится
на 3?
Поскольку 333=3х111, 666=3х222, 999=3*333, то многие учащиеся, отвечая на вопрос, называют число 555.
Но это неверно, так как 555=3*185. Правильный ответ: Никакое.
2-й подтип. Задачи, побуждающие сделать неправильный выбор ответа из предложенных верных и неверных ответов. Что легче: пуд пуха или пуд железа?
Многие полагают, что пуд пуха легче, поскольку железо тяжелее пуха. Но этот ответ неверен: пуд железа имеет массу - 16кг и масса пуда пуха тоже - 16кг.
Поскольку 333=3х111, 666=3х222, 999=3*333, то многие учащиеся, отвечая на вопрос, называют число 555.
Но это неверно, так как 555=3*185. Правильный ответ: Никакое.
2-й подтип. Задачи, побуждающие сделать неправильный выбор ответа из предложенных верных и неверных ответов. Что легче: пуд пуха или пуд железа?
Многие полагают, что пуд пуха легче, поскольку железо тяжелее пуха. Но этот ответ неверен: пуд железа имеет массу - 16кг и масса пуда пуха тоже - 16кг.
I тип. Задачи, навязывающие в явной форме один вполне определённый ответ.
Слайд 381. Тройка лошадей проскакала 15 км. Сколько км проскакала каждая лошадь?
Хочется выполнить деление 15:3 и тогда ответ: 5 км. На самом деление выполнять совсем не требуется, поскольку каждая лошадь проскакала столько же, сколько и тройка.
2. (Старинная задача) Шёл мужик в Москву, а навстречу ему шли 7 богомолок, у каждой из них было по мешку, а в каждом мешке – по коту. Сколько существ направлялось в Москву?
Решающий с трудом удерживается от того, чтобы сказать: «15 существ, так как 1+7+7=15», но ответ неверен, сумму находить не требуется. Ведь в Москву шёл один мужик.
II тип. Задачи, условия которых подталкивают решающего к тому, чтобы выполнить какое-либо действие с заданными числами или величинами, тогда как выполнять это действие вовсе не требуется.
Слайд 391. Три спички выложены на столе так, что получилось четыре. Могло
ли такое быть, если других предметов на столе не было?
Напрашивающийся отрицательный ответ опровергается рисунком
2. (Старинная задача) Крестьянин продал на рынке трёх коз за три рубля. Спрашивается: «По чему каждая коза пошла?»
Очевидный ответ: «По одному рублю» - опровергается: козы по деньгам не ходят, ходят по земле.
Напрашивающийся отрицательный ответ опровергается рисунком
2. (Старинная задача) Крестьянин продал на рынке трёх коз за три рубля. Спрашивается: «По чему каждая коза пошла?»
Очевидный ответ: «По одному рублю» - опровергается: козы по деньгам не ходят, ходят по земле.
III тип. Задачи, условия которых допускают возможность «опровержения» семантически верного решения синтаксическим или иным нематематическим решением
Слайд 411. Коротышки из цветочного городка посадили арбуз. Для его полива требуется
ровно 1л воды. У них есть только 2 пустых бидона ёмкостью 3л и 5л. Как, пользуясь этими бидонами, набрать из реки ровно 1л воды?
Решение: Представим решение в таблице.
Составим выражение: 3*2-5=1. Необходимо 2 раза наполнить трёхлитровый сосуд и один раз опустошить пятилитровый.
Решение: Представим решение в таблице.
Составим выражение: 3*2-5=1. Необходимо 2 раза наполнить трёхлитровый сосуд и один раз опустошить пятилитровый.
Задачи, решаемые составлением таблицы.
Слайд 42Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и
арабский. На вопрос, какой язык изучает каждый из них, один ответил: ''Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский”. Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей?
Решение нестандартных логических задач с помощью рассуждений.
Решение. Имеется три утверждения:
Вадим изучает китайский;
Сергей не изучает китайский;
Михаил не изучает арабский.
Если верно первое утверждение, то верно и второе, так как юноши изучают разные языки. Это противоречит условию задачи, поэтому первое утверждение ложно.
Если верно второе утверждение, то первое и третье должны быть ложны. При этом получается, что никто не изучает китайский. Это противоречит условию, поэтому второе утверждение тоже ложно.
Остается считать верным третье утверждение, а первое и второе - ложными. Следовательно, Вадим не изучает китайский, китайский изучает Сергей.
Ответ: Сергей изучает китайский язык, Михаил - японский, Вадим - арабский.
Слайд 43Подготовительная группа:
Учим выделять существенные признаки
Учим ребёнка сравнивать.
Учим классифицировать предметы.
«Что общего?»
«Что лишнее?».
«Что объединяет?»
Специфика работы
Слайд 44Для детей со средним и низким уровнем развития необходимо давать задачи
с обязательной опорой:
На схемы, чертежи, таблицы.
Ключевые слова, которые позволяют лучше усвоить содержание задачи, выбрать способ записи.
На схемы, чертежи, таблицы.
Ключевые слова, которые позволяют лучше усвоить содержание задачи, выбрать способ записи.
Специфика работы
Слайд 45Решение нестандартных задач формирует у учащихся умения высказывать предположения, проверять их
достоверность, логически обосновывать. Проговаривание с целью доказательства, способствует развитию речи учащихся, выработке умения делать выводы из посылок, строить умозаключения.
Выполняя творческие задания, учащиеся анализируют условия, выделяют существенное в предложенной ситуации, соотносят данные и искомое, выделяют связи между ними.
Выполняя творческие задания, учащиеся анализируют условия, выделяют существенное в предложенной ситуации, соотносят данные и искомое, выделяют связи между ними.
Заключение.
Слайд 46Сухомлинский наблюдал за ходом мышления детей, и наблюдения подтвердили, «что, прежде
всего надо научить детей охватывать мысленным взором ряд предметов, явлений, событий, осмысливать связи между ними.
Изучая мышление тугодумов, я всё больше убеждался, что неумение осмыслить, например, задачу - следствие неумения абстрагироваться, отвлекаться от конкретного. Надо научить ребят мыслить абстрактными понятиями».
Изучая мышление тугодумов, я всё больше убеждался, что неумение осмыслить, например, задачу - следствие неумения абстрагироваться, отвлекаться от конкретного. Надо научить ребят мыслить абстрактными понятиями».
ВЫВОД
