- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Основы теории электрических цепей презентация
Содержание
- 1. Основы теории электрических цепей
- 2. 26.11.09 ОТЭЦ В осеннем/весеннем семестрах: Лекции- 34/18
- 3. 26.11.09 Расчет несимметричных трехфазных цепей методом симметричных составляющих. Преобразование Фортескью. (C.L.Fortescue, USA, 1918).
- 4. 26.11.09 Метод симметричных составляющих - мсс
- 5. 26.11.09 Мсс используется для расчета несимметричных (аварийных)
- 6. 26.11.09 В динамических трехфазных цепях имеется индуктивная связь между фазами, которую удобно учесть, используя мсс.
- 7. 26.11.09 Этот метод основан на разложении трехфазной
- 8. 26.11.09
- 9. 26.11.09 +j +1
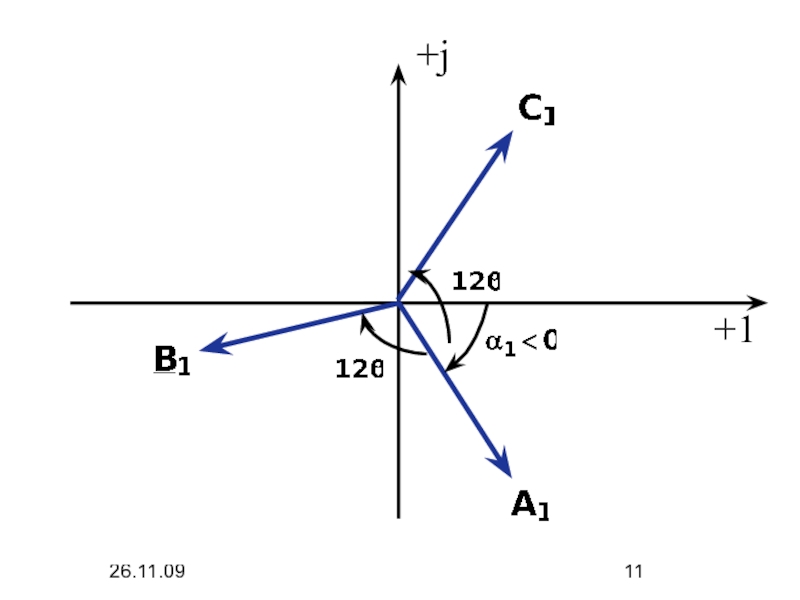
- 10. 26.11.09 1. Составляющие прямой последовательности
- 11. 26.11.09 +j +1
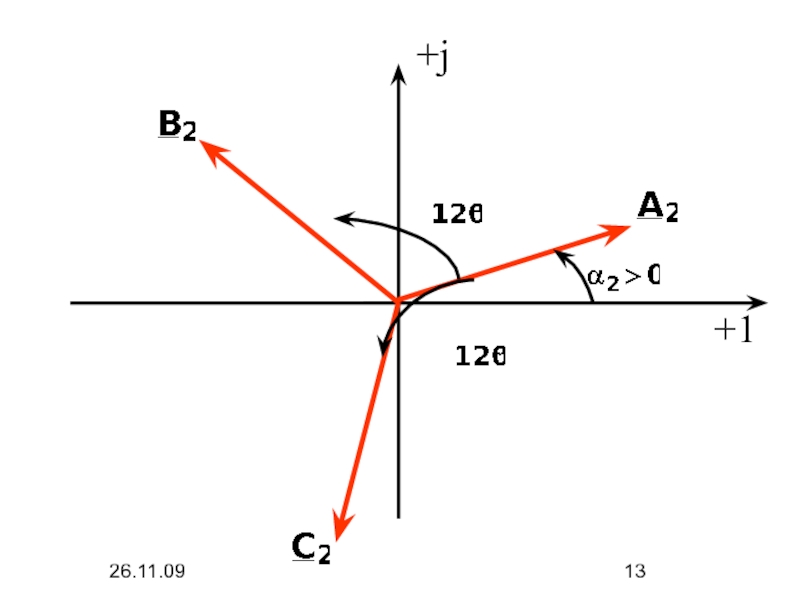
- 12. 26.11.09 2. Составляющие обратной последовательности
- 13. 26.11.09 +j +1
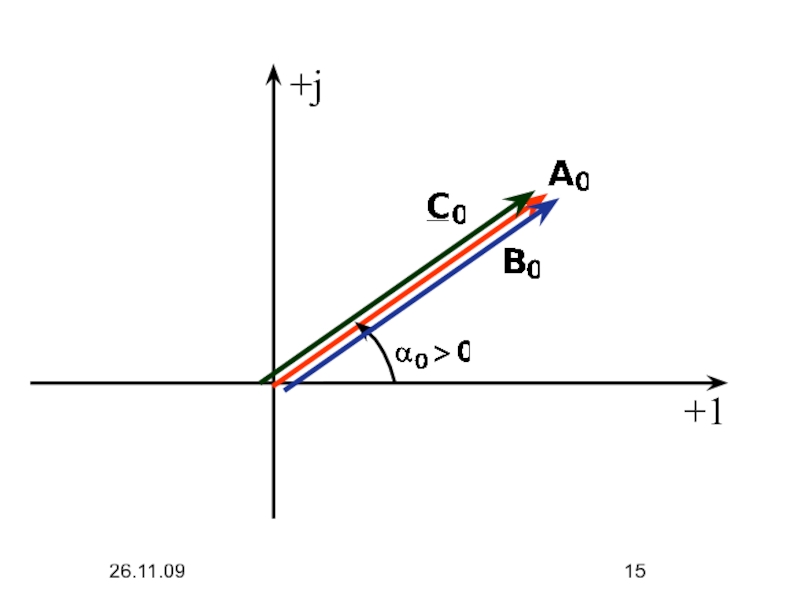
- 14. 26.11.09 3. Составляющие нулевой последовательности
- 15. 26.11.09 +j +1
- 16. 26.11.09 Расчет составляющих фазы А:
- 17. 26.11.09 Составляющие токов прямой последовательности создают магнитное
- 18. 26.11.09 Составляющие токов обратной последовательности создают магнитное поле, вращающееся навстречу вращению роторов двигателей и генераторов
- 19. 26.11.09 Составляющие токов нулевой последовательности создают неподвижное пульсирующее магнитное поле.
- 20. 26.11.09 Таким образом условия протекания составляющих токов
- 21. 26.11.09 Естественно, в линейной трехфазной цепи имеет
- 22. 26.11.09
- 23. 26.11.09 Фазные токи:
- 24. 26.11.09 Составляющие фазных напряжений:
- 25. 26.11.09 Фазные напряжения:
- 26. 26.11.09 Это означает, что расчет симметричной трехфазной
- 27. 26.11.09 Построим симметричные составляющие для
- 28. 26.11.09
- 29. 26.11.09 Прямой и обратный переходы от несимметричной
- 30. 26.11.09
- 31. 26.11.09 Их удобно удобно записывать в матричном виде:
- 32. 26.11.09
- 33. 26.11.09
- 34. 26.11.09
- 35. 26.11.09 Отношения комплексных фазных напряжений прямой, обратной
- 36. 26.11.09 В цепях со статическими нагрузками, т.е.
- 37. 26.11.09
- 38. 26.11.09
- 39. 26.11.09
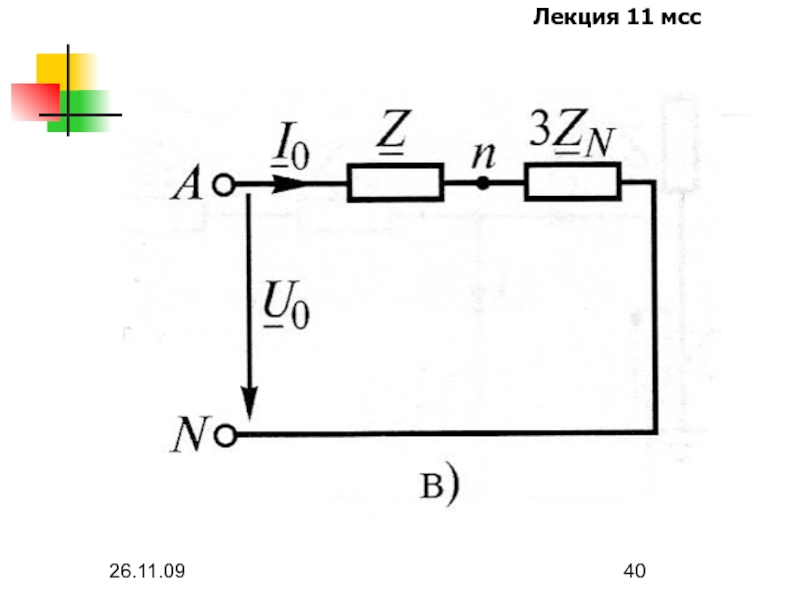
- 40. 26.11.09
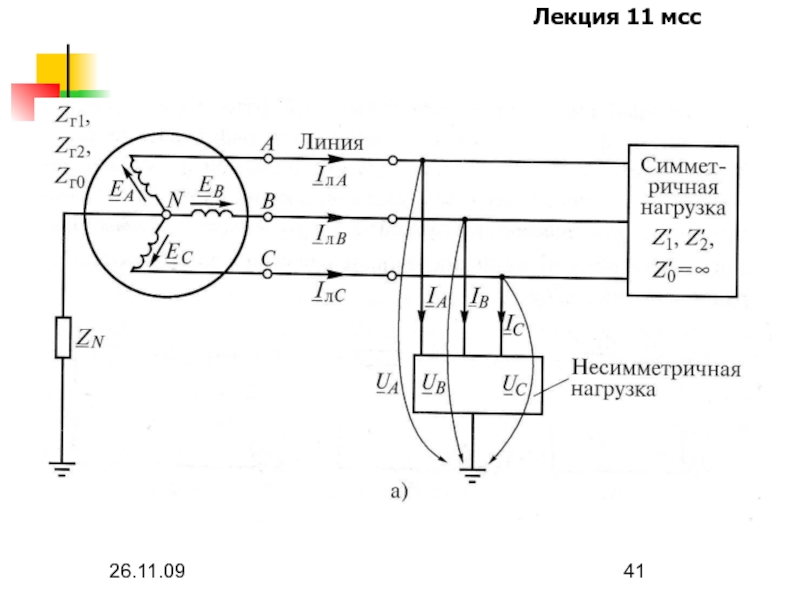
- 41. 26.11.09
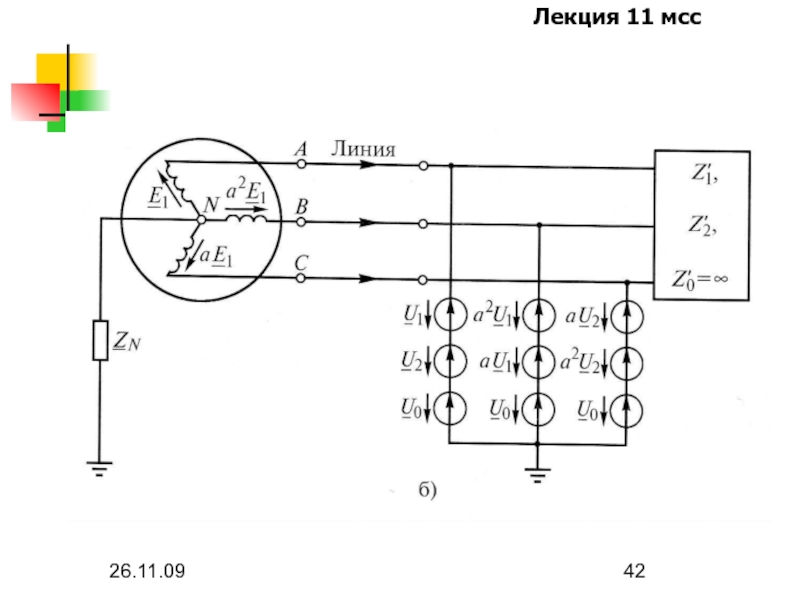
- 42. 26.11.09
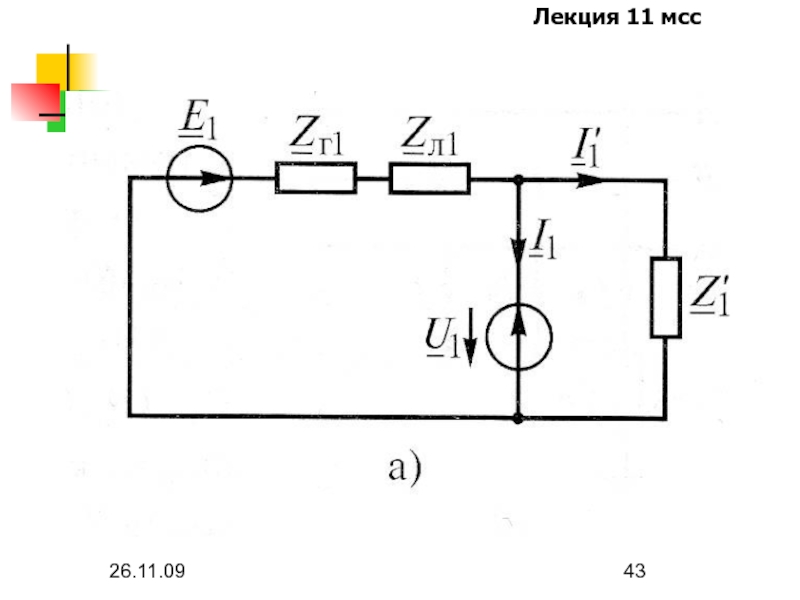
- 43. 26.11.09
- 44. 26.11.09
- 45. 26.11.09
- 46. 26.11.09
- 47. 26.11.09
- 48. 26.11.09 Особенности существования составляющих напряжений и токов нулевой последовательности
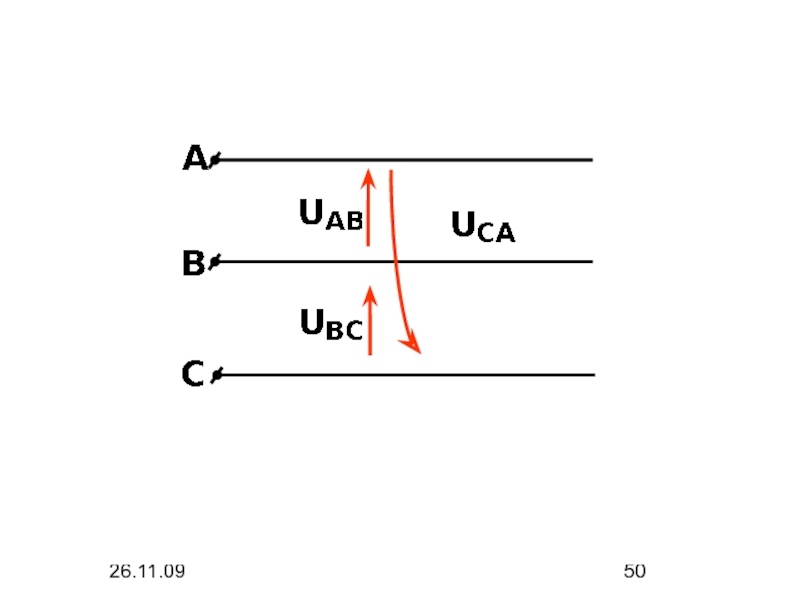
- 49. 26.11.09 1. Линейные напряжения
- 50. 26.11.09
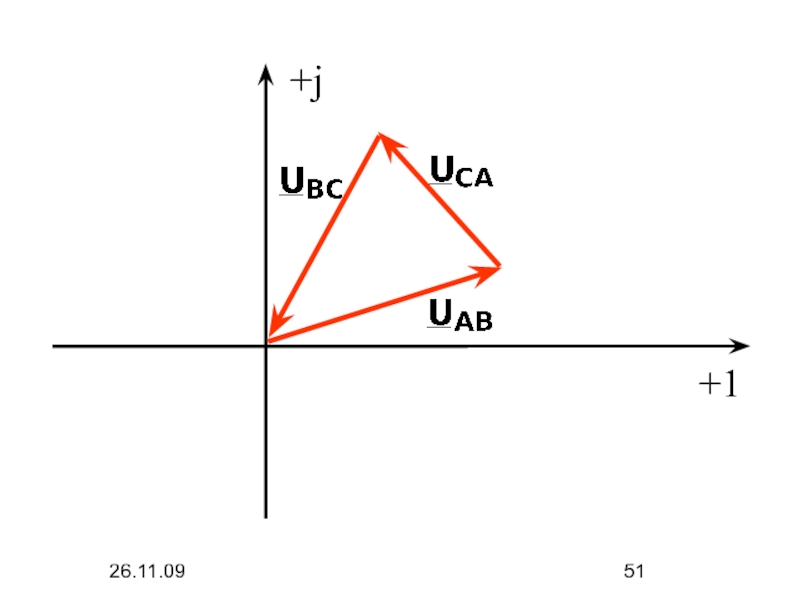
- 51. 26.11.09 +j +1
- 52. 26.11.09
- 53. 26.11.09 Линейные напряжения не содержат составляющих нулевой последовательности
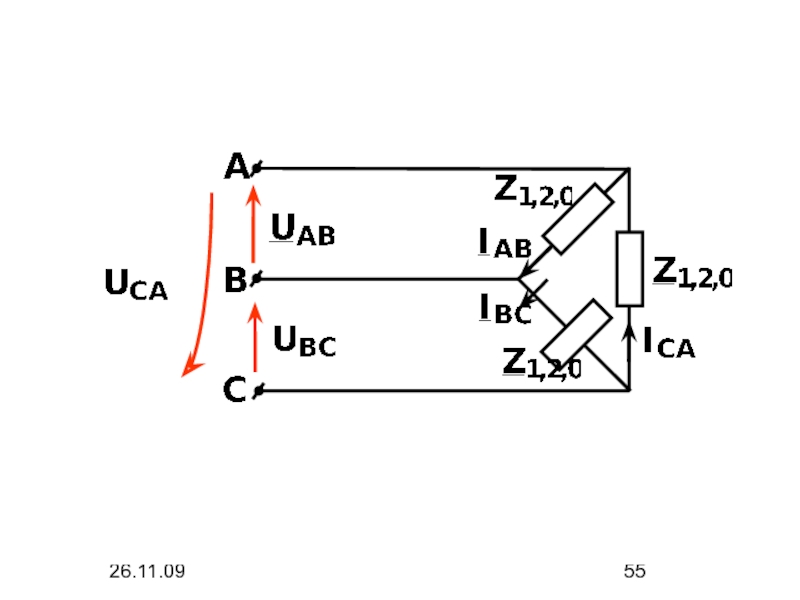
- 54. 26.11.09 2. Фазные токи треугольника
- 55. 26.11.09
- 56. 26.11.09 Так как То
- 57. 26.11.09 Фазные токи нагрузки, соединенной в треугольник, не содержат составляющих нулевой последовательности.
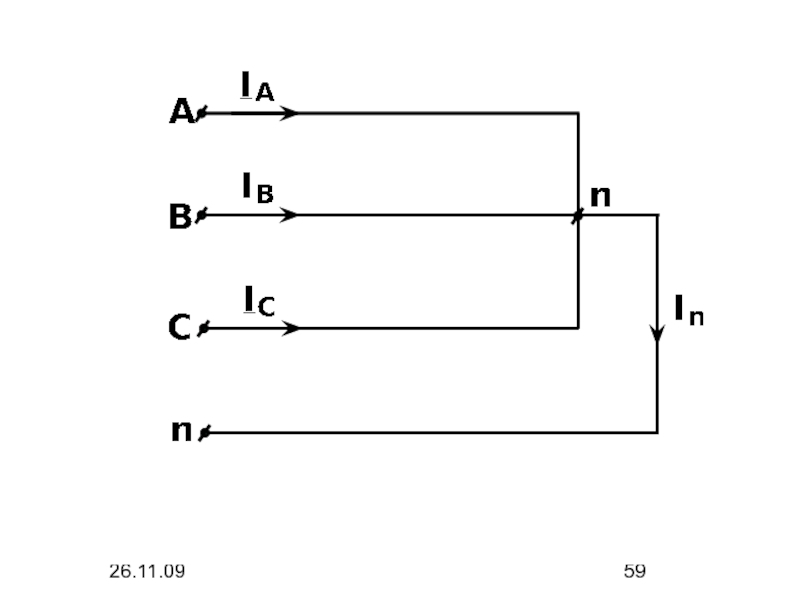
- 58. 26.11.09 3. Ток нулевого провода
- 59. 26.11.09
- 60. 26.11.09 Так как То
- 61. 26.11.09 Линейные токи звезды и пропорциональные им
Слайд 226.11.09
ОТЭЦ
В осеннем/весеннем семестрах:
Лекции- 34/18 час.
Лаборатория- 18/18 час.
Практические занятия- 18/18 час.
Компьютер. практика-
18/18 час.
Экзамен- зима/весна
Экзамен- зима/весна
Слайд 326.11.09
Расчет несимметричных трехфазных цепей
методом симметричных составляющих.
Преобразование Фортескью.
(C.L.Fortescue, USA, 1918).
Слайд 526.11.09
Мсс используется для расчета несимметричных (аварийных) режимов динамических трехфазных цепей, содержащих
генераторы, двигатели, лэп, трансформаторы и др. элементы необязятельно 3-х фазные.
Слайд 626.11.09
В динамических трехфазных цепях имеется индуктивная связь между фазами, которую удобно
учесть, используя мсс.
Слайд 726.11.09
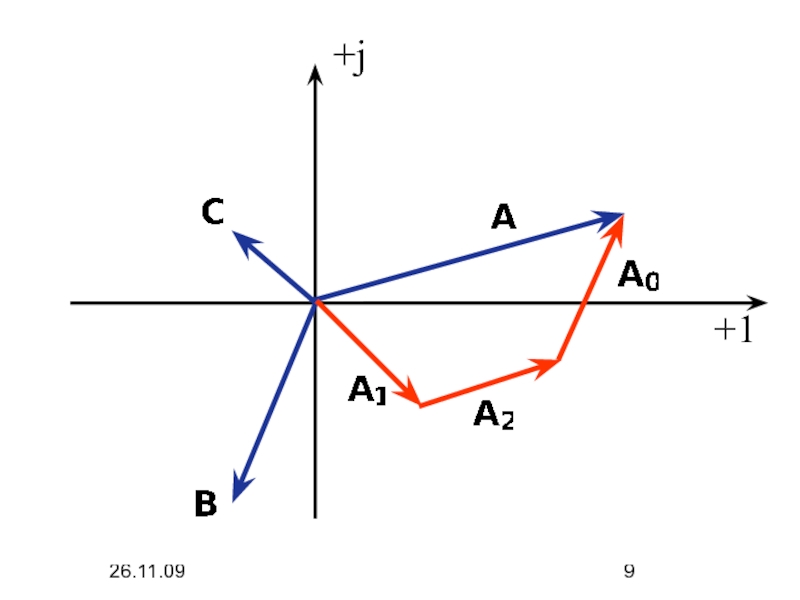
Этот метод основан на разложении трехфазной несимметричной системы
A ,B ,C
на симметричные составляющие прямой (A1,B1,C1), обратной (A2,B2,C2),
и нулевой (A0,B0,C0) последовательностей.
Слайд 1726.11.09
Составляющие токов прямой последовательности создают магнитное поле, вращающееся по направлению вращения
роторов двигателей и генераторов
Слайд 1826.11.09
Составляющие токов обратной последовательности создают магнитное поле, вращающееся навстречу вращению роторов
двигателей и генераторов
Слайд 1926.11.09
Составляющие токов нулевой последовательности создают неподвижное пульсирующее магнитное поле.
Слайд 2026.11.09
Таким образом условия протекания составляющих токов разные, следовательно, и сопротивления этим
составляющим разные:
у двигателей и генераторов
у линий и трансформаторов
Слайд 2126.11.09
Естественно, в линейной трехфазной цепи имеет место независимость действия симметричных составляющих
токов и напряжений различной последовательности.
Следовательно, можно применять метод наложения.
Слайд 2626.11.09
Это означает, что расчет симметричной трехфазной цепи можно вести на одну
фазу для каждой последовательности отдельно.
Слайд 2726.11.09
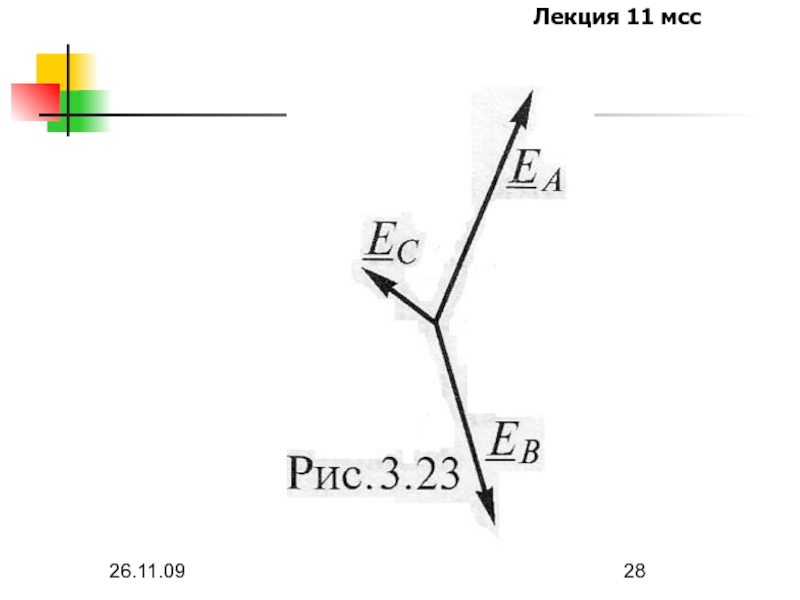
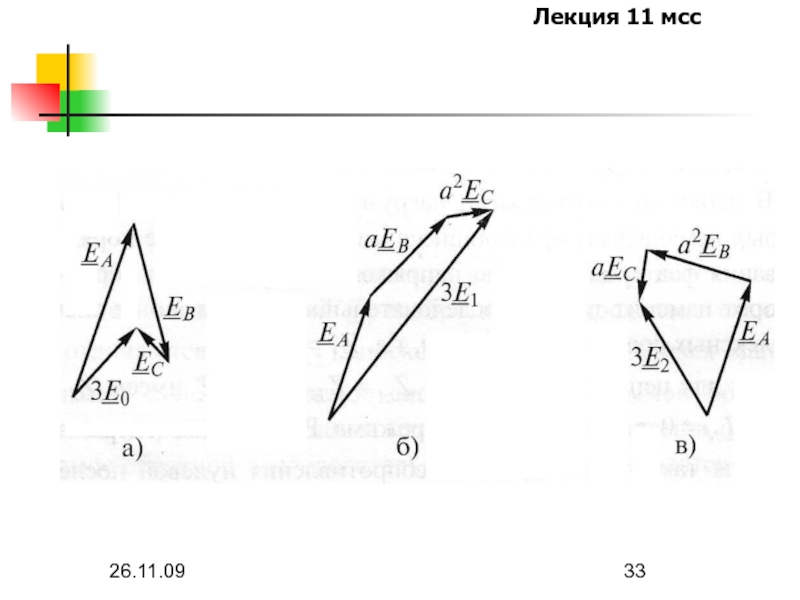
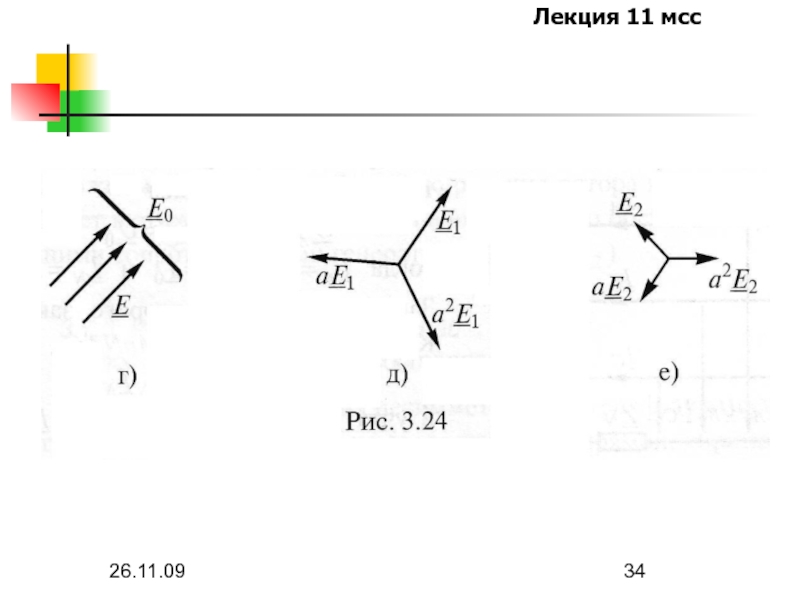
Построим симметричные составляющие для несимметричной 3-х фазной системы ЭДС, заданных
графически на следующей картинке.
Слайд 2926.11.09
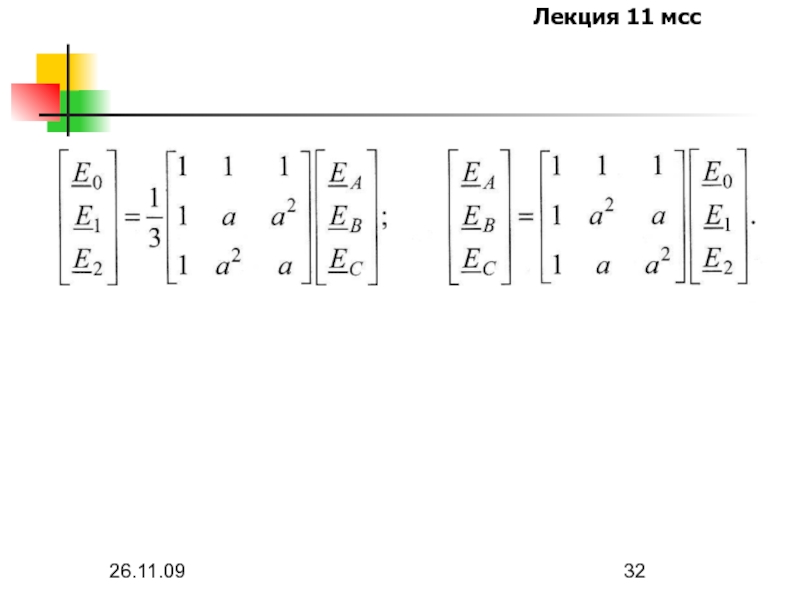
Прямой и обратный переходы от несимметричной системы ЭДС к трем её
симметричным составляющим даётся уже указанным преобразованием, называемым иногда преобразованием Фортескью:
Слайд 3526.11.09
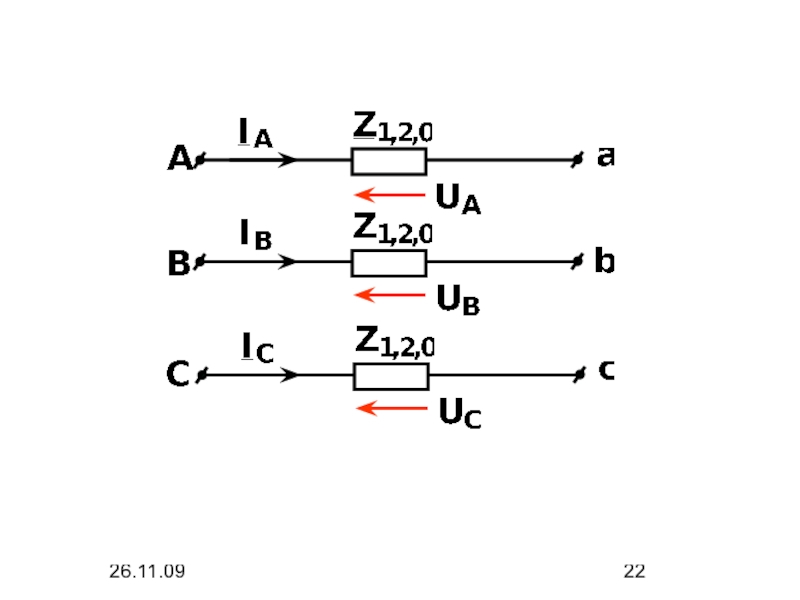
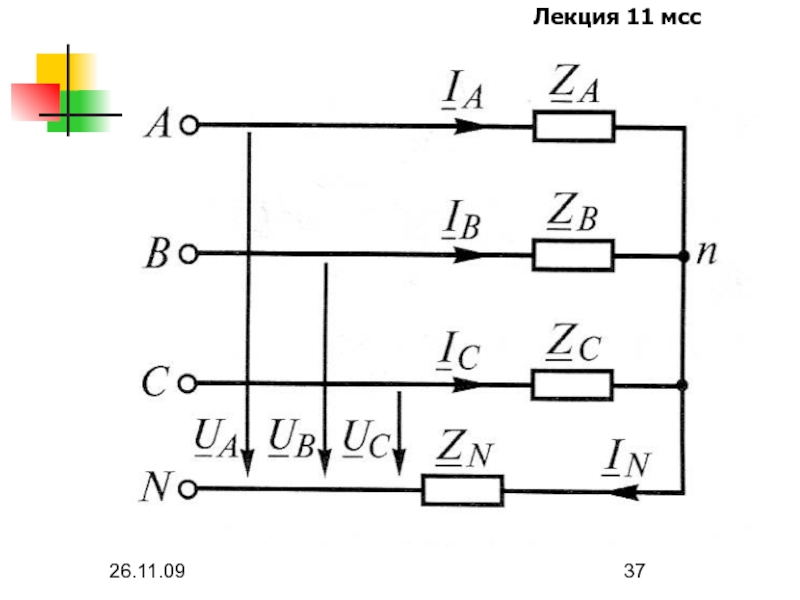
Отношения комплексных фазных напряжений прямой, обратной и нулевой последовательности к соответствующим
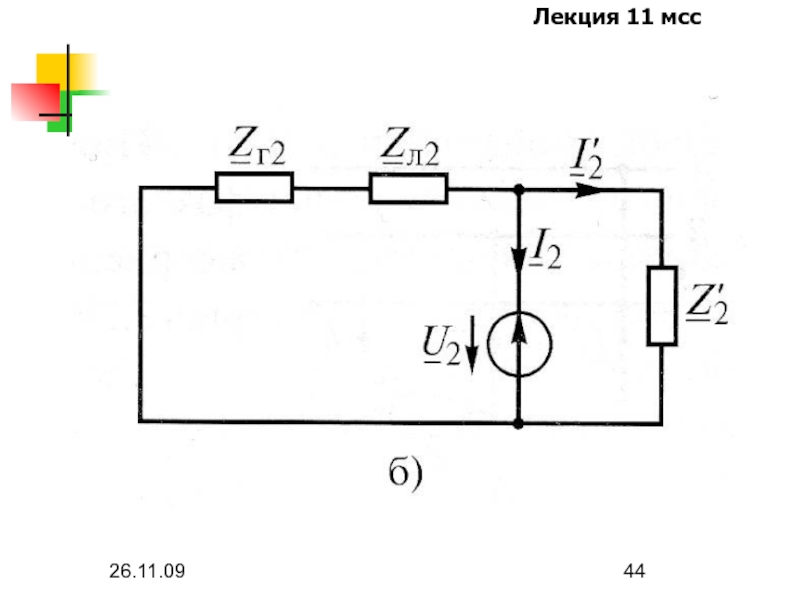
комплексным фазным токам называют комплексными сопротивлениями цепи прямой (Z1), обратной (Z2) и нулевой (Z0) последовательностей.
Слайд 3626.11.09
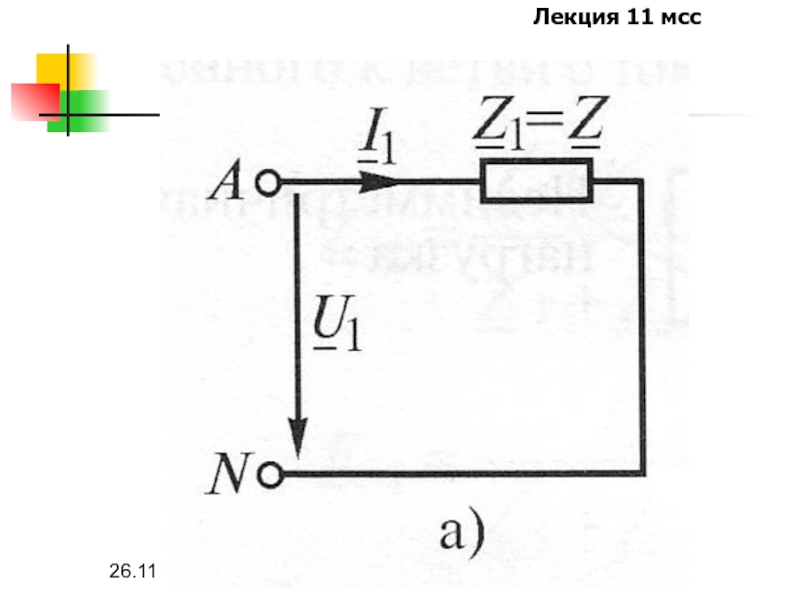
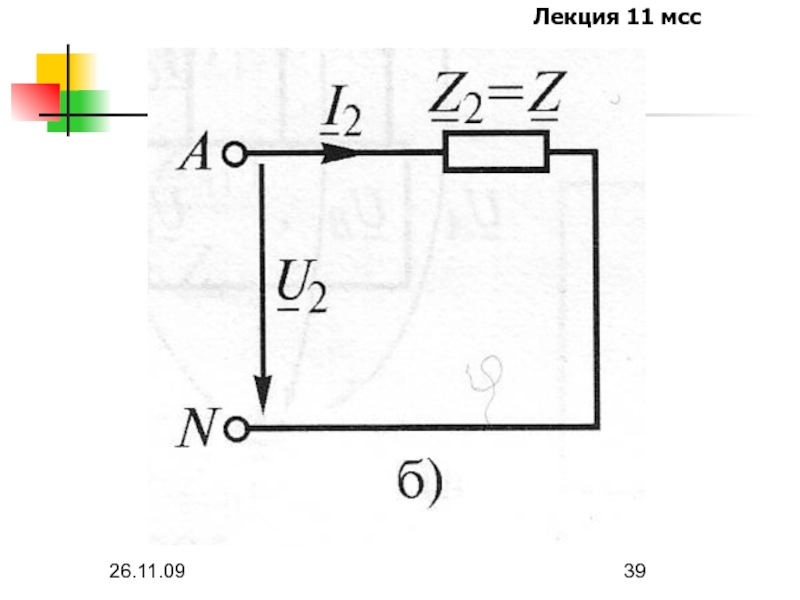
В цепях со статическими нагрузками, т.е. в цепях, приемники которых не
содержат вращающиеся машины, изменение порядка чередования фаз приложенного напряжения с прямого на обратный и наоборот изменит только последовательность токов, но не значения комплексных сопротивлений цепи, т.е. Z1=Z2.
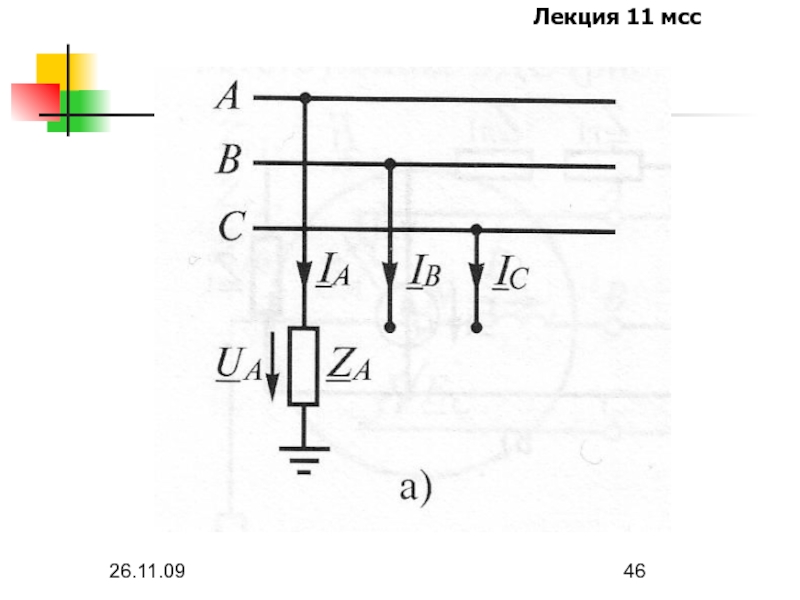
Слайд 4826.11.09
Особенности существования составляющих напряжений и токов нулевой последовательности
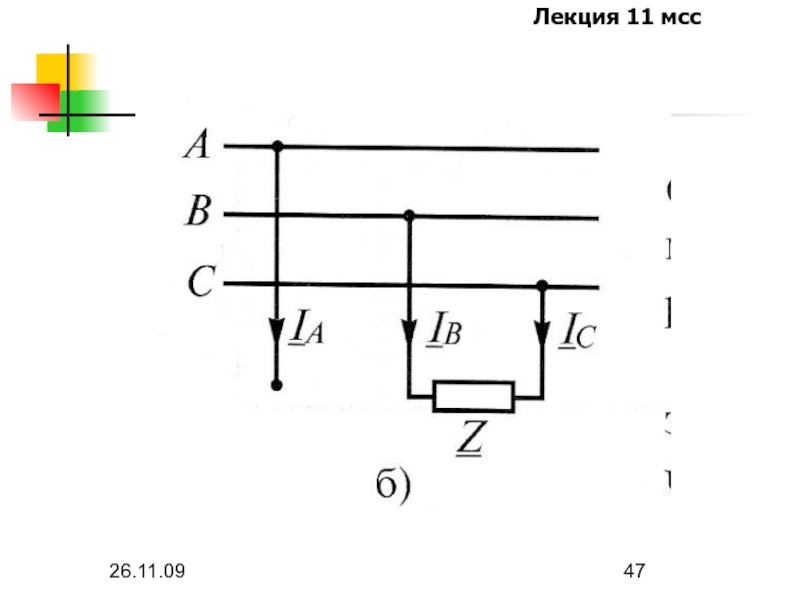
Слайд 5726.11.09
Фазные токи нагрузки, соединенной в треугольник, не содержат составляющих нулевой последовательности.
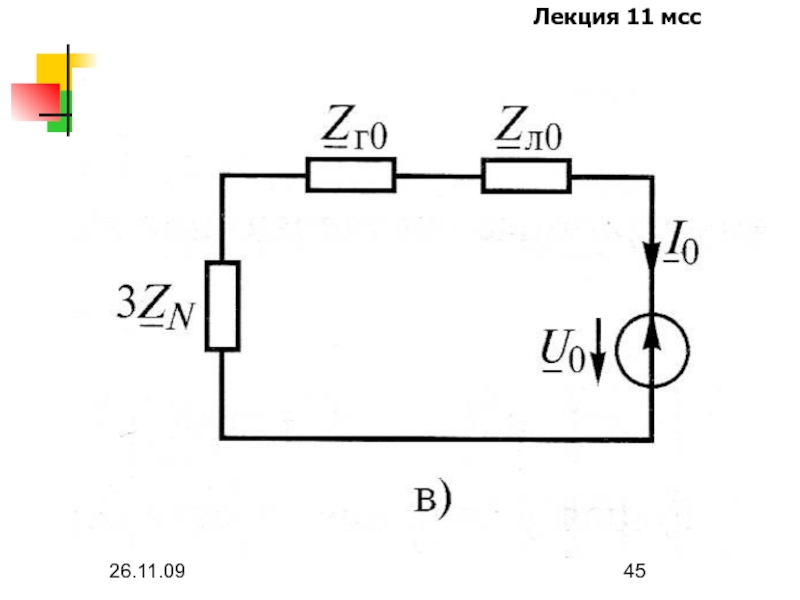
Слайд 6126.11.09
Линейные токи звезды и пропорциональные им фазные напряжения содержат составляющие нулевой
последовательности при наличии нулевого провода или связи с “землей”, причем в нулевом проводе протекают
только составляющие токов нулевой последовательности