Основы логики презентация

Автор: Соколов Кирилл
Дата: 19. 03. 11 г.
Учитель: Ковалева Ю.В.

Формы мышления
2 Алгебра высказываний
2.1 Логическое умножение ( конъюнкция)
2.2 Логическое сложение (дизъюнкция)
2.3 Логическое отрицание (инверсия)
3.1 Логические выражения и таблицы истинности
3.2 Логические выражения и таблицы истинности
4.1 Логические функции
4.2 Логические функции
5.1 Логические законы и правила преобразования логических выражений
5.2 Логические законы и правила преобразования логических выражений

существенные признаки предмета.
Высказывание- форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может быть либо истинно, либо ложно.
Умозаключение- форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение).

которые могут принимать лишь два значения: «истина» (1) и «ложь» (0).
Базовые логические операции («и», «или», «не»)
1 Логическое умножение (конъюнкция)
2 Логическое сложение (дизъюнкция)
3 Логическое отрицание (инверсия)

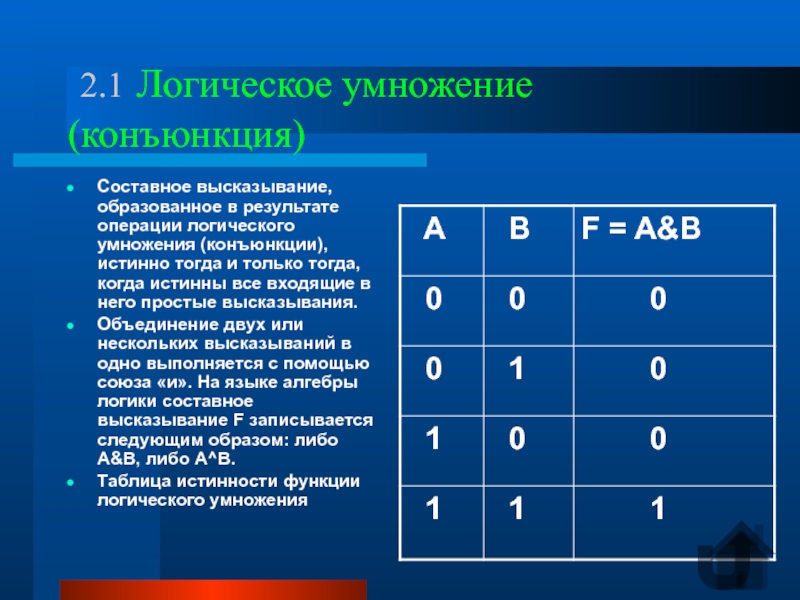
операции логического умножения (конъюнкции), истинно тогда и только тогда, когда истинны все входящие в него простые высказывания.
Объединение двух или нескольких высказываний в одно выполняется с помощью союза «и». На языке алгебры логики составное высказывание F записывается следующим образом: либо A&B, либо A^B.
Таблица истинности функции логического умножения

(дизъюнкции), истинно тогда, когда истинно хотя бы одно из входящих в него высказываний.
Объединение двух или нескольких высказываний происходит с помощью союза «или». На языке алгебры логики составное высказывание F записывается следующим образом: A+B
Таблица истинности функции логического сложения.

наоборот, ложное- истинным.
Присоединение частицы «не» к высказыванию называется операцией логического отрицания. На языке алгебры логики высказывание F записывается таким способом: F = A.
Таблица истинности функции логического отрицания

высказывание можно выразить с помощью формулы (логического выражения), в которую входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.
Для записи составного высказывания в виде логического выражения на языке алгебры логики в составном высказывании нужно выделить простые высказывания и логические связи между ними.

При этом необходимо соблюдать определённый порядок действий: 1 Определить количество строк в таблице истинности.
2 Необходимо определить количество столбцов в таблице истинности
3 Нужно построить таблицу истинности с указанным количеством строк и столбцов.
4 Необходимо заполнить таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности и в соответствии с их таблицами истинности.

Равносильные логические выражения – логические выражения, у которых последние столбцы таблиц истинности совпадают.

3.2 Логические выражения и таблицы истинности

в одно с помощью оборота речи «если…, то…». Логическая операция импликации «если А, то В», обозначается А В и выражается с помощью логической функции F14, которая задаётся соответствующей таблицей истинности.

речи «… тогда и только тогда, когда…». Логическая операция эквивалентности «А тогда и только тогда, когда В» обозначается А~В и выражается с помощью логической функции F10, которая задаётся соответствующей таблицей истинности.

4.2 Логические функции

А=А
Закон непротиворечия- А*А=0
Закон исключённого третьего- А+А=1
Закон двойного отрицания- А=А
Закон де Моргана- А+В= А+В, А*В=А+В
Закон коммутативности
А*В=В*А А+В=В+А
Закон ассоциативности
(А*В)*С= А*(В*С) (А+В)+С=А+(В+С)

(А+В)*(А+С)= А+(В*С)
Закон поглощения
А+(А*В)=А
Примеры преобразования выражений:
А*(В+В)= А*1=А
(А*В)+(А*В)=А*(В+В)=А

5.2 Логические законы и правила преобразования логических выражений

внимание