- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Определенный интеграл презентация
Содержание
- 1. Определенный интеграл
- 2. Понятие определенного интеграла Пусть на отрезке [a,b]
- 3. 2. Построение интегральной суммы. Выберем на каждом отрезке
- 4. 3. Предельный переход. Найдем теперь предел
- 5. Почему удобно использовать ЭВМ для расчетов ОИ
- 6. Известно, что определенный интеграл функции
- 7. Некоторые методы вычисления определенного интеграла с помощью
- 8. f(x) x a x1 x2
- 9. Метод Трапеций Интеграл равен сумме
- 10. Метод средних прямоугольников. Интеграл равен сумме
- 11. Метод Симпсона Разделим отрезок [a,b] на четное
- 12. Проблемы точного вычисления определенных интегралов.
- 13. Сравнение результатов расчетов на [0;
- 14. Еще несколько примеров ∫(x+1)dx = 6 на
- 15. Заключение и выводы. В настоящее время
- 16. Источники «Лекции по программированию. Язык программирования С.»
Слайд 1Определенный интеграл
И
некоторые методы приближенного вычисления определенного интеграла
с помощью ЭВМ
(методы
Слайд 2Понятие определенного интеграла
Пусть на отрезке [a,b] задана функция f(x). Построение понятия
1. Разбиение отрезка [a,b] на части.
Разобьем отрезок [a, b] на части точками так что
длина i-го «кусочка»
максимальная из этих длин.
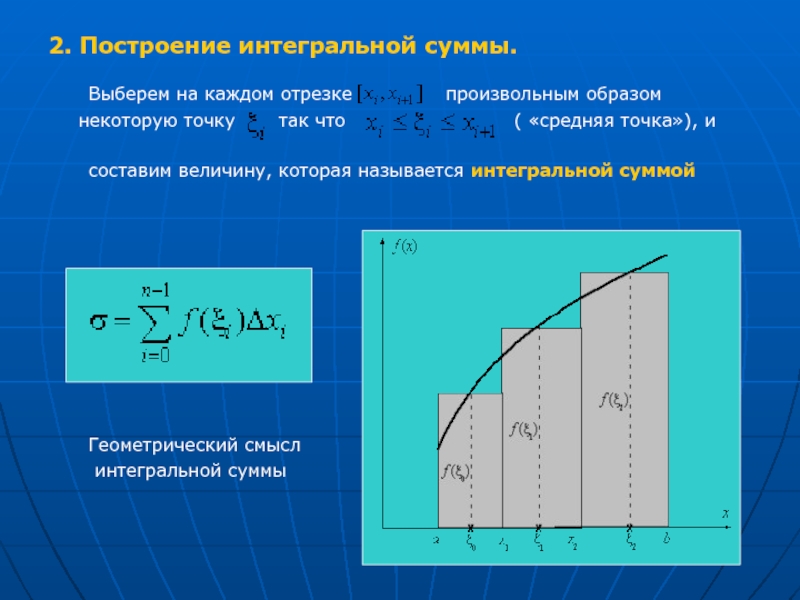
Слайд 32. Построение интегральной суммы.
Выберем на каждом отрезке
составим величину, которая называется интегральной суммой
Геометрический смысл
интегральной суммы
Слайд 43. Предельный переход.
Найдем теперь предел
Определение. Если существует
а) от способа разбиения отрезка на части
б) от способа выбора средней точки,
то говорят, что есть определенный интеграл
от функции f(x) по отрезку [a, b].
Функция f(x) называется интегрируемой на отрезке
[a, b], a и b - нижний и верхний пределы интегрирования соответственно.
Слайд 5Почему удобно использовать ЭВМ для расчетов ОИ ?
При решении многих задач
ЭВМ также быстро находит значение интегралов, для которых первообразная непрерывной функции f(x) не выражается через элементарные функции. В этом случае использование формулы Ньютона-Лейбница весьма затруднительно.
Слайд 6
Известно, что определенный интеграл функции
Типа
численно представляет собой площадь криволинейной трапеции ограниченной кривыми y=f(x), x=a, x=b и y=0
Криволинейная трапеция.
То есть, вычислив площадь криволинейной трапеции, мы получим значение определенного интеграла.
На этом основаны методы вычисления определенного интеграла с помощью ЭВМ.
Слайд 7Некоторые методы вычисления
определенного интеграла
с помощью ЭВМ
Метод трапеций
Метод средних прямоугольников
Метод Симпсона
Метод
и другие…
Слайд 8
f(x)
x
a x1 x2 x3 x4 ... b
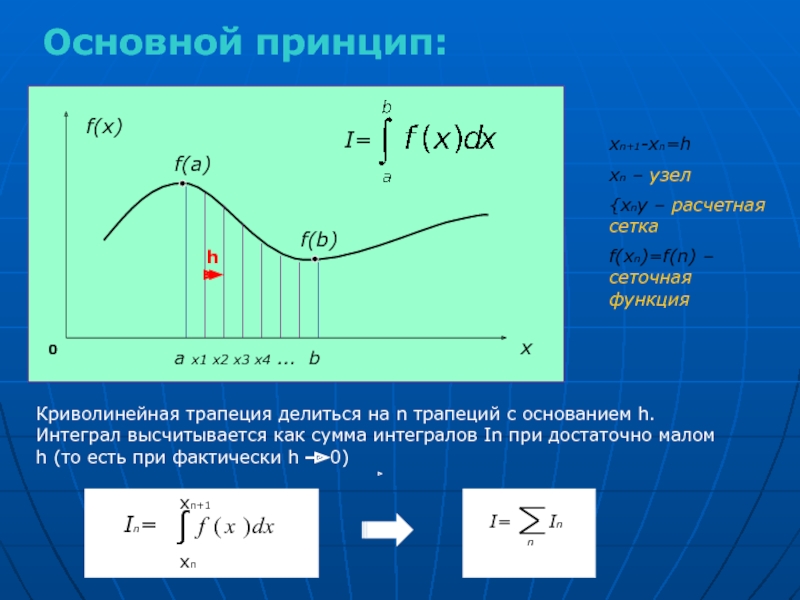
I=
xn+1-xn=h
xn – узел
{xny – расчетная
f(xn)=f(n) – сеточная функция
Криволинейная трапеция делиться на n трапеций с основанием h. Интеграл высчитывается как сумма интегралов In при достаточно малом h (то есть при фактически h 0)
h
In=
0
I= In
n
f(a)
f(b)
Основной принцип:
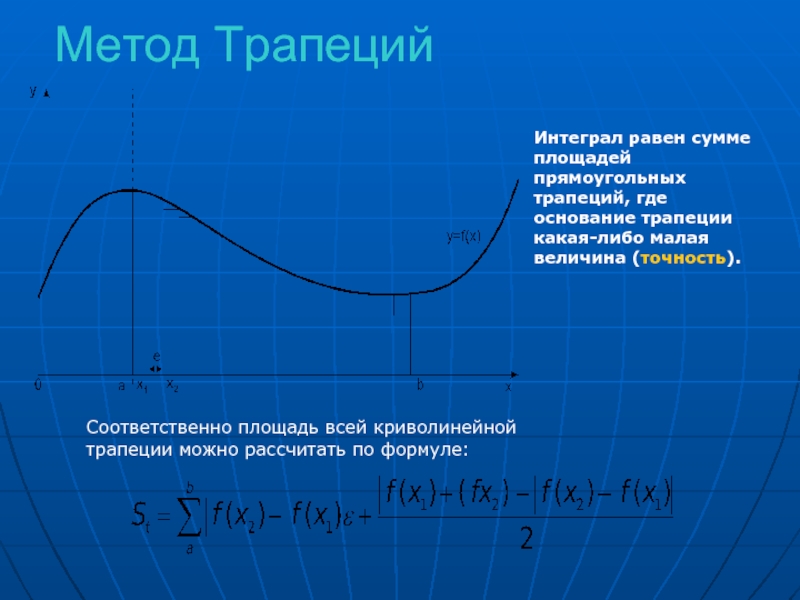
Слайд 9Метод Трапеций
Интеграл равен сумме площадей прямоугольных трапеций, где основание трапеции какая-либо
Соответственно площадь всей криволинейной трапеции можно рассчитать по формуле:
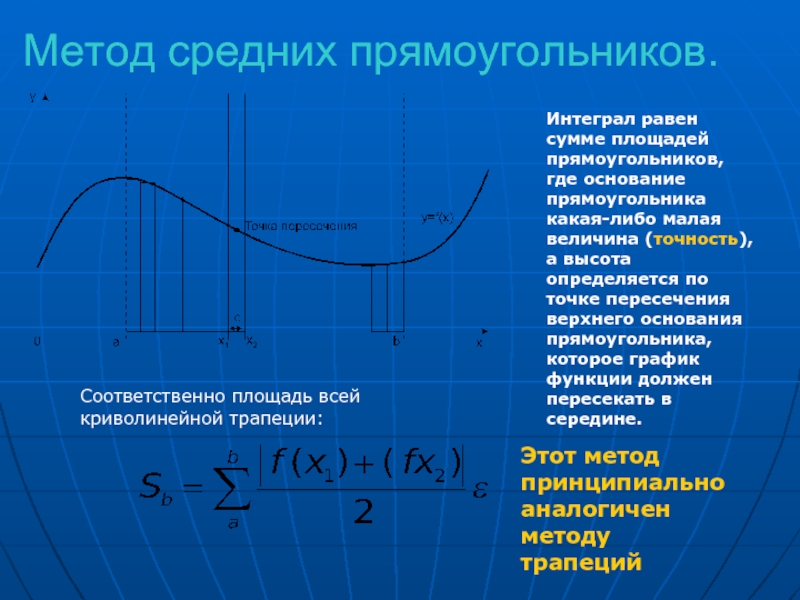
Слайд 10Метод средних прямоугольников.
Интеграл равен сумме площадей прямоугольников, где основание прямоугольника какая-либо
Соответственно площадь всей криволинейной трапеции:
Этот метод принципиально аналогичен методу трапеций
Слайд 11Метод Симпсона
Разделим отрезок [a,b] на четное число равных частей n =
Уравнение параболы с осью, ll Оу, имеет вид
y = Ax*х + Bx + C.
Коэффициенты А, В и С однозначно определяются по трем точкам.
Аналогичные параболы строим и для других пар отрезков. Сумма площадей параболических трапеций и даст приближенное значение интеграла.
Формула Симпсона:
, где уi=f(xi)
Слайд 13Сравнение результатов расчетов
на [0; ]
n=1000
на [0;1]
при
на [0;1] n=1000
Из этих трех методов более точные результаты дает метод Симпсона.
Однако, изменяя n мы можем получить достаточно точный результат с помощью любого метода.
Слайд 14Еще несколько примеров
∫(x+1)dx = 6 на [1;3] ; ∫ (x*x)dx =
(По формуле Ньютона-Лейбница).
Результаты, полученные на ЭВМ с использованием метода трапеций:
Слайд 15Заключение и выводы.
В настоящее время ЭВМ решают множество задач, для которых
Очевидно, что вычисление определенных интегралов методами трапеций, средних прямоугольников и методом Симпсона не дает нам точного значения, а только приближенное.
Чем ниже задается численное значение точности вычислений (основание трапеции), тем точнее результат получаемый машиной. При этом, число итераций составляет обратно пропорциональное от численного значения точности. Следовательно для большей точности необходимо большее число итераций, что обуславливает возрастание затрат времени вычисления интеграла на компьютере обратно пропорционально точности вычисления.
Использование для вычисления одновременно нескольких методов позволило исследовать зависимость точности вычислений при применении этих методов.
Следовательно при понижении численного значения точности вычислений результаты расчетов по всем методам стремятся друг к другу и все - к точному результату.
Слайд 16Источники
«Лекции по программированию. Язык программирования С.» Белошапкин В.В. Copyright © Красноярский
«Основы математического анализа », Ильин В.А., Позняк Э.Г., Физический факультет МГУ, изд. Физматлит, 2002 г.
Вольвачев А.Н., Крисевич В.С., «Программирование на языке Паскаль для ПЭВМ ЕС». Минск.: 1989 г.
Зуев Е.А. «Язык программирования Turbo Pascal». М.1992 г.
Белорусский Аграрный Технический Университет, Кафедра вычислительной техники, Курсовая работа: “Вычисление определенного интеграла методами трапеций и средних прямоугольников” студента 2-го курса, Полушкина О.А., Минск, 1997 г.
Магнитогорский Государственный Технический Университет, Курсовая работа: «Приближенное вычисление определенных интегралов. Формула Парабол (Формула Симпсона)» студента группы ФГК-98, Григоренко М.В., Магнитогорск, 1999 г.

![Понятие определенного интеграла Пусть на отрезке [a,b] задана функция f(x). Построение понятия определенного интеграла от этой](/img/tmb/3/204547/6c640f9a0433b278d583ec4774d9ce14-800x.jpg)




![Метод СимпсонаРазделим отрезок [a,b] на четное число равных частей n = 2m. Площадь криволинейной трапеции,](/img/tmb/3/204547/999c5a1dd65a35a55987bb29ad7c2fd4-800x.jpg)

![Сравнение результатов расчетовна [0; ] n=1000на [0;1] при различных nна [0;1] n=1000Из этих трех](/img/tmb/3/204547/a11e2bc08ea3dfdf3fe56e097d878411-800x.jpg)
![Еще несколько примеров∫(x+1)dx = 6 на [1;3] ; ∫ (x*x)dx = 9 на [0;3]; (По](/img/tmb/3/204547/1bdbb19f0f90c991283d354ab3455178-800x.jpg)







