Калачёв Максим Александрович
Разработчик
kalachevmax@gmail.com
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
О том, как Computer Science нам жить помогает или современные приложения теории графов презентация
Содержание
- 1. О том, как Computer Science нам жить помогает или современные приложения теории графов
- 2. Agenda веб-графы методы моделирования ранжирование неестественные структуры shortest path problem нерешённые проблемы
- 3. Метафизический вопрос №1
- 4. Метафизический вопрос №2
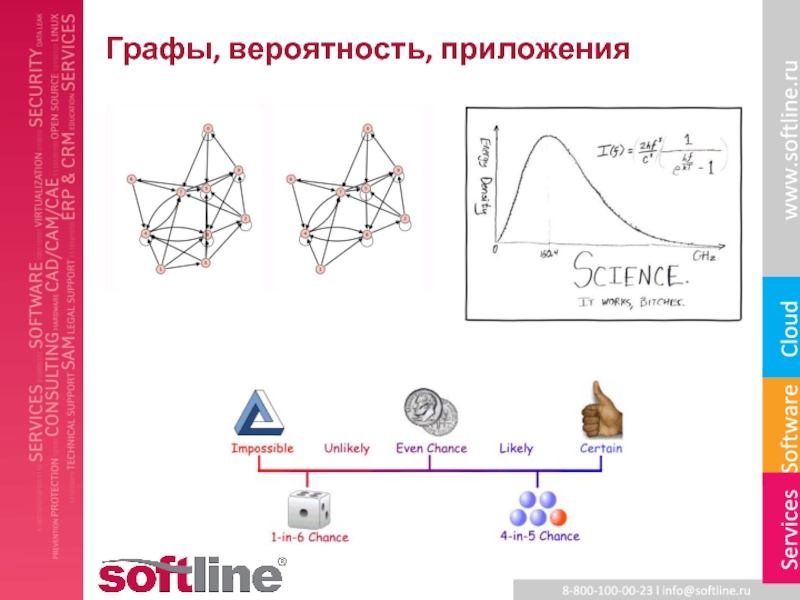
- 5. Графы, вероятность, приложения
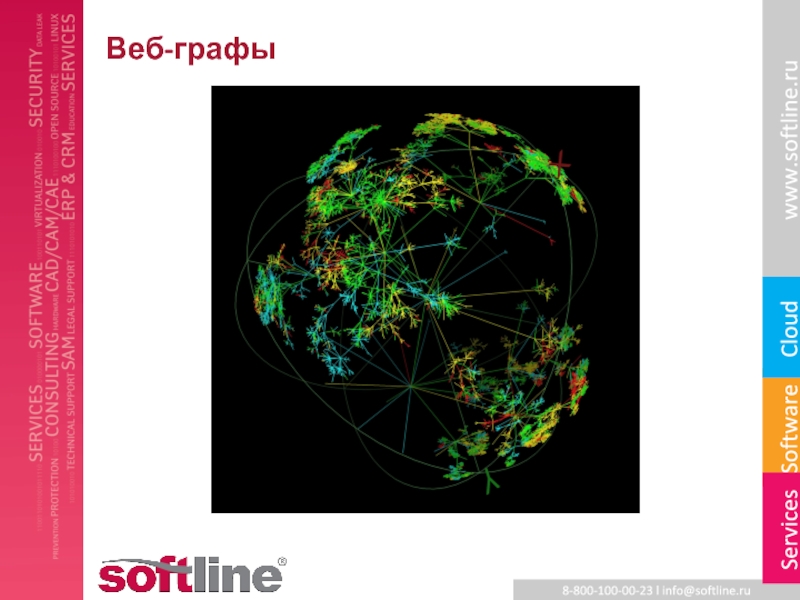
- 6. Веб-графы
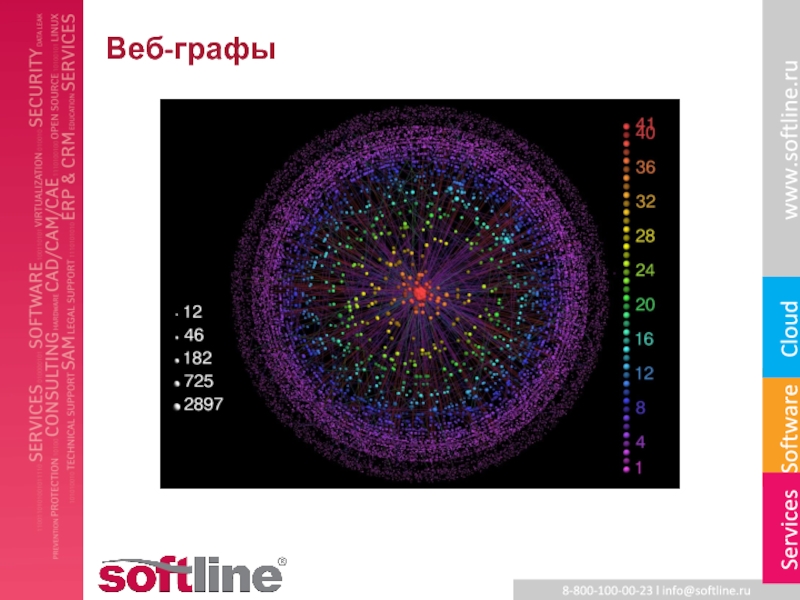
- 7. Веб-графы
- 8. Веб-графы
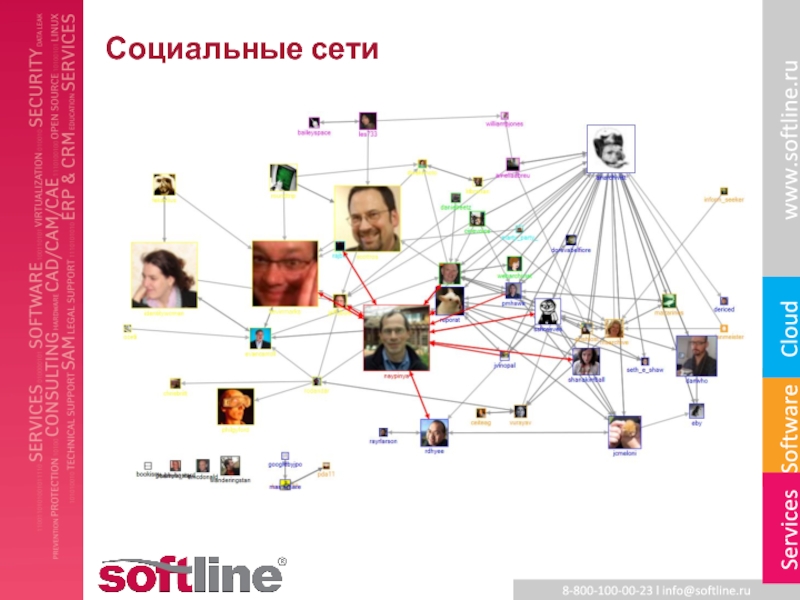
- 9. Социальные сети
- 10. Социальные сети
- 11. Моделирование веб-графов Случайные графы Исследования Barabasi-Albert Модель Bollobas-Riordan Модификации модели
- 12. Как устроен веб-граф? Albert-Laszlo Barabasi and Reka
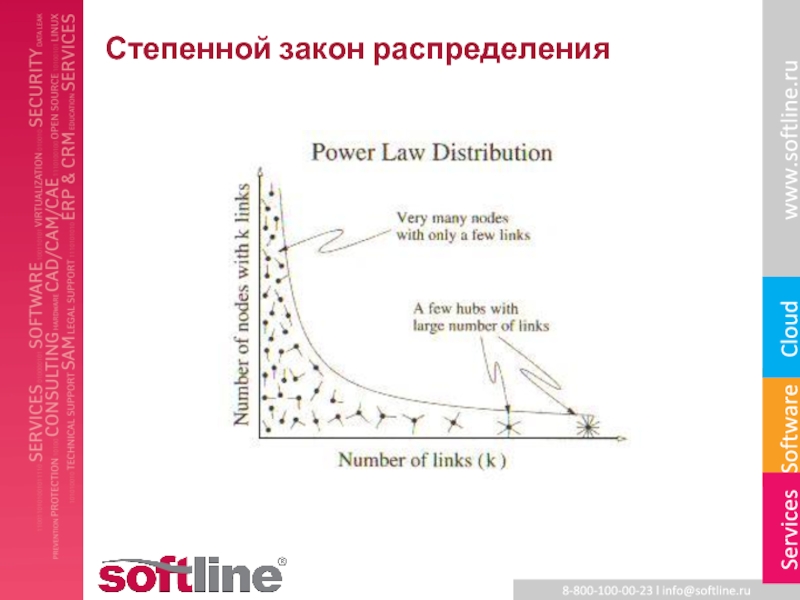
- 13. Степенной закон распределения
- 14. Эволюция веб-графа Модель предпочтительного соединения (preferential attachment)
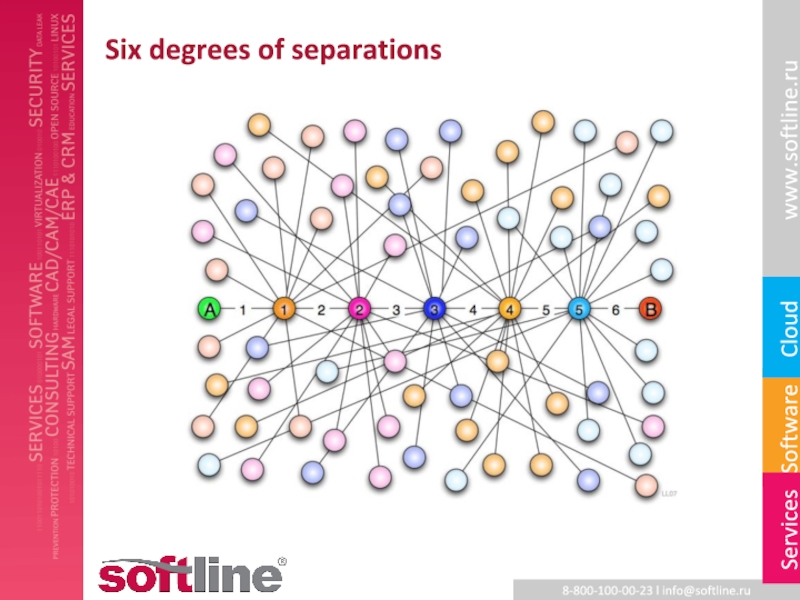
- 15. Six degrees of separations
- 16. Six degrees of separations
- 17. Масштабная инвариантность
- 18. Scale-free networks Техника: Сети электропередачи, VLSI, Интернет,
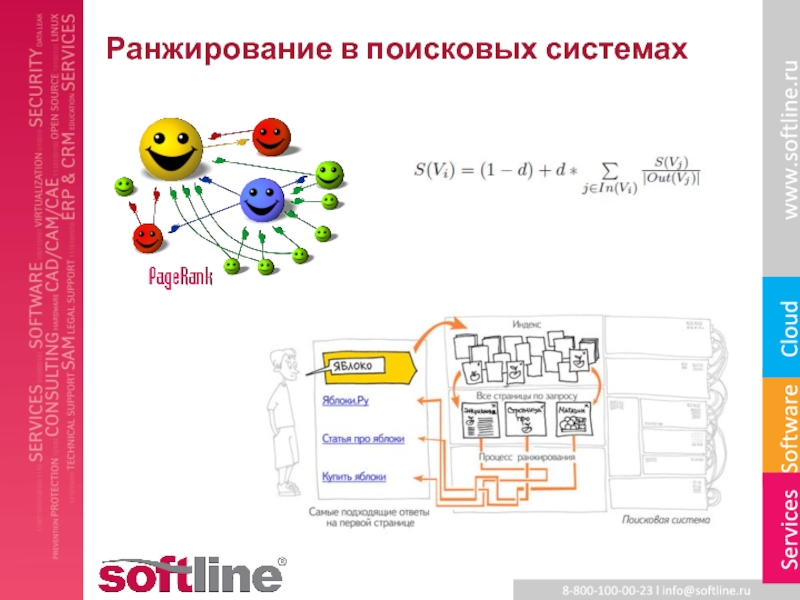
- 19. Ранжирование в поисковых системах
- 20. Ранжирование в семантических сетях проект WordNet (wordnet.princeton.edu)
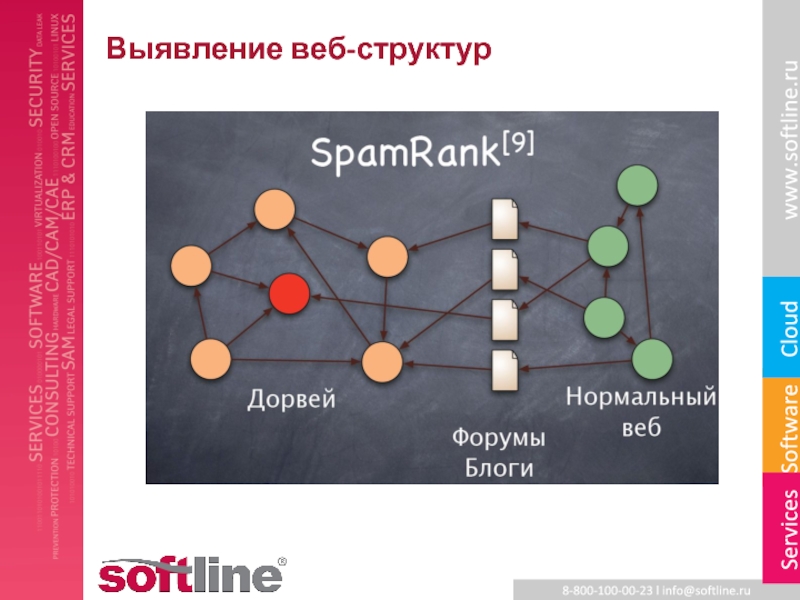
- 21. Выявление веб-структур
- 22. Выявление веб-структур
- 23. Shortest path problem Andrew Goldberg Microsoft Research
- 24. Shortest path problem Почему современные алгоритмы на
- 25. Нерешённые вопросы Самое главное, что ученик должен
- 26. P vs NP NP – класс всех
- 27. Послесловие Я.Б. Зельдович считал, что постановка задачи
Слайд 1О том, как Computer Science нам жить помогает или современные приложения
теории графов
Слайд 2Agenda
веб-графы
методы моделирования
ранжирование
неестественные структуры
shortest path problem
нерешённые проблемы
Слайд 11Моделирование веб-графов
Случайные графы
Исследования Barabasi-Albert
Модель Bollobas-Riordan
Модификации модели
Слайд 12Как устроен веб-граф?
Albert-Laszlo Barabasi and Reka Albert. Emergence of scaling in
random networks. Science, 286:509, 1999.
5 млрд вершин, псевдомультиорграф
Ключевые свойства веб-графа:
∙ Разрежённость
на k вершин kt рёбер, k ≥ 1
∙ Диаметр графа ∈ {5, 6}
Теория о шести рукопожатиях
∙ Степенное распределение степеней вершин
P(d) ∼ c / d λ
λ ≈ 2.1, c – нормирующий множитель
5 млрд вершин, псевдомультиорграф
Ключевые свойства веб-графа:
∙ Разрежённость
на k вершин kt рёбер, k ≥ 1
∙ Диаметр графа ∈ {5, 6}
Теория о шести рукопожатиях
∙ Степенное распределение степеней вершин
P(d) ∼ c / d λ
λ ≈ 2.1, c – нормирующий множитель
Слайд 18Scale-free networks
Техника: Сети электропередачи, VLSI, Интернет, Веб
Социум: контакты, связи, организации, язык,
дороги, авиамаршруты
Биология: нейроны; пищевые, экологические, метаболические сети
Физика: молекулы, галактики
Биология: нейроны; пищевые, экологические, метаболические сети
Физика: молекулы, галактики
Слайд 24Shortest path problem
Почему современные алгоритмы на картах работают очень быстро
100000 млн
вершин
Время работы 10-2 c
Интуитивные идеи:
Указатели на дугах
Поиск A*
Достижимость
Шоссейная и желаемые иерархии
Перевалочные пункты
Время работы 10-2 c
Интуитивные идеи:
Указатели на дугах
Поиск A*
Достижимость
Шоссейная и желаемые иерархии
Перевалочные пункты
Слайд 25Нерешённые вопросы
Самое главное, что ученик должен узнать от учителя - это
что некоторый вопрос ещё не решён.
Петровский И.Г.
Петровский И.Г.
brainware
hardware
Слайд 26P vs NP
NP – класс всех задач поиска, решение для которых
может быть быстро проверено.
P – класс задач поиска, решение для которых может быть быстро найдено.
P ≠ NP – верно ли, что каждый раз, когда решение можно быстро проверить, его можно быстро найти.
P – класс задач поиска, решение для которых может быть быстро найдено.
P ≠ NP – верно ли, что каждый раз, когда решение можно быстро проверить, его можно быстро найти.
Слайд 27Послесловие
Я.Б. Зельдович считал, что постановка задачи – искусство куда более тонкое,
чем решение. “Стоит точно сформулировать вопрос, - говорил он, - как тотчас найдётся подходящий математик для решения. Ведь математики, они как мухи, - умеют ходить по потолку!”
В.И. Арнольд, Задачи Арнольда.
В.И. Арнольд, Задачи Арнольда.