- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Новый Робот в новых задачах презентация
Содержание
- 1. Новый Робот в новых задачах
- 2. Система команд исполнителя РОБОТ, «живущего» в прямоугольном
- 3. Если РОБОТ начнёт движение в сторону находящейся
- 4. Решение 1. Указанные записи циклов ПОКА аналогичны
- 5. Решение 2. Внутренние циклы определяют перемещение РОБОТа
- 6. Решение Определяем клетки лабиринта, имеющие стенки и
- 7. Решение Анализируем диапазон A1:F1: достаточно проанализировать клетку
- 8. Решение Анализируем диапазон A2:F2: достаточно проанализировать клетку
- 9. Решение Анализируем диапазон A3:F3: достаточно проанализировать клетку
- 10. Решение Анализируем диапазон A4:F4: достаточно проанализировать клетку
- 11. Решение Анализируем диапазон A5:D5: достаточно проанализировать клетку
- 12. Решение Анализируем диапазон E5:F5: достаточно проанализировать клетку
- 13. Решение Анализируем диапазон A6:F6: достаточно проанализировать клетку
- 14. Решение Итого (зеленый цвет – клетки, являющиеся
Слайд 2Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости:
При
Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ:
Цикл
ПОКА <условие>
последовательность команд
КОНЕЦ ПОКА
выполняется, пока условие истинно.
В конструкции
ЕСЛИ <условие>
ТО команда1
ИНАЧЕ команда2
КОНЕЦ ЕСЛИ
выполняется команда1 (если условие истинно) или команда2 (если условие ложно)
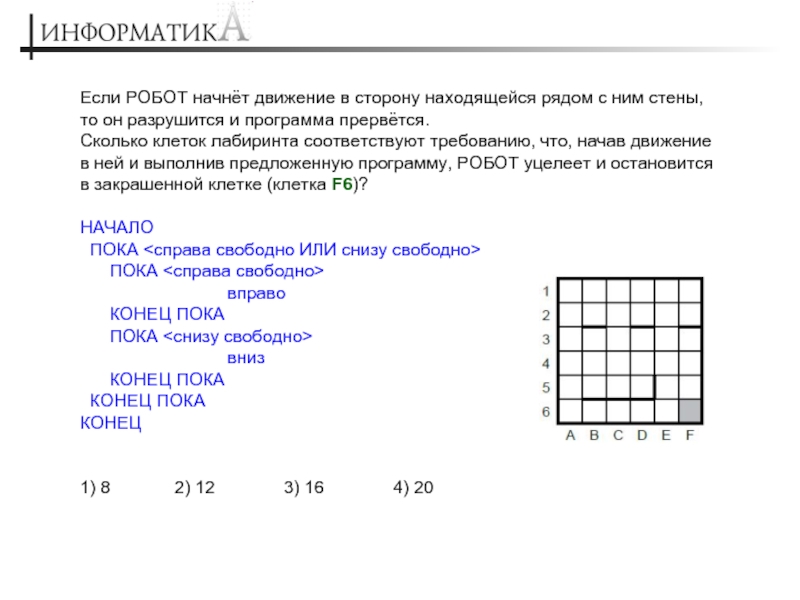
Слайд 3Если РОБОТ начнёт движение в сторону находящейся рядом с ним стены,
Сколько клеток лабиринта соответствуют требованию, что, начав движение в ней и выполнив предложенную программу, РОБОТ уцелеет и остановится в закрашенной клетке (клетка F6)?
НАЧАЛО
ПОКА <справа свободно ИЛИ снизу свободно>
ПОКА <справа свободно>
вправо
КОНЕЦ ПОКА
ПОКА <снизу свободно>
вниз
КОНЕЦ ПОКА
КОНЕЦ ПОКА
КОНЕЦ
1) 8 2) 12 3) 16 4) 20
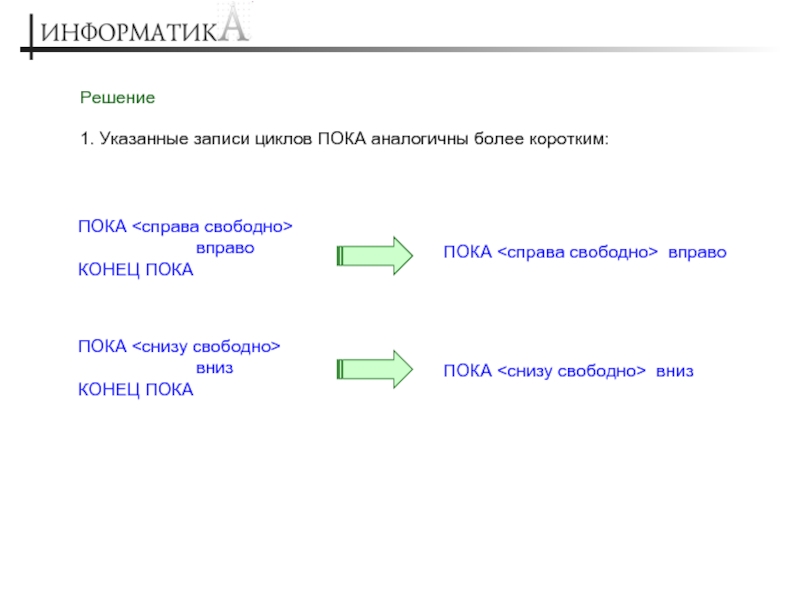
Слайд 4Решение
1. Указанные записи циклов ПОКА аналогичны более коротким:
ПОКА
вправо
КОНЕЦ ПОКА
ПОКА <справа свободно> вправо
ПОКА <снизу свободно>
вниз
КОНЕЦ ПОКА
ПОКА <снизу свободно> вниз
Слайд 5Решение
2. Внутренние циклы определяют перемещение РОБОТа в соответствующем
направлении
3. Внешний цикл означает, что «Г-образное» движение РОБОТа,
определяемое двумя внутренними циклами, может быть повторено,
если после остановки РОБОТа из-за препятствия снизу выяснится,
что справа препятствия нет.
4. Завершение движения РОБОТа – в клетке, которая имеет препятствия
(стенки) и снизу, и справа. Причем проверка этого условия производится
только после выполнения обоих вложенных циклов.
5. Любой из вложенных циклов ПОКА осуществляет движение РОБОТа
до препятствия. Поэтому можно разбить весь лабиринт на полоски
«равноправных» клеток: если какая-то из них является решением,
то решением являются и все остальные клетки этой полоски, и наоборот.
Слайд 6Решение
Определяем клетки лабиринта, имеющие стенки и справа, и снизу:
Клетка F6 –
Разбиваем лабиринт на диапазоны «равноправных» клеток:
A1:F1, A2:F2, A3:F3, A4:F4, A5:D5, E5:F5, A6:F6
Слайд 7Решение
Анализируем диапазон A1:F1: достаточно проанализировать клетку A1:
Из всех клеток этого диапазона
Слайд 8Решение
Анализируем диапазон A2:F2: достаточно проанализировать клетку A2:
Из всех клеток этого диапазона
Слайд 9Решение
Анализируем диапазон A3:F3: достаточно проанализировать клетку A3:
Из всех клеток этого диапазона
Слайд 10Решение
Анализируем диапазон A4:F4: достаточно проанализировать клетку A4:
Из всех клеток этого диапазона
Слайд 11Решение
Анализируем диапазон A5:D5: достаточно проанализировать клетку A5:
Из всех клеток этого диапазона
Слайд 12Решение
Анализируем диапазон E5:F5: достаточно проанализировать клетку E5:
Из всех клеток этого диапазона
Слайд 13Решение
Анализируем диапазон A6:F6: достаточно проанализировать клетку A6:
Из всех клеток этого диапазона
Слайд 14Решение
Итого (зеленый цвет – клетки, являющиеся решениями; оранжевый цвет – клетки,
Решениями задачи являются: 6 клеток диапазона A3:F3, 6 клеток диапазона A4:F4, 2 клетки диапазона E5:F5 и 6 клеток диапазона A6:F6 (включая саму клетку F6), т. е. всего 6 + 6 + 2 + 6 = 20 ячеек.
Ответ: вариант 4.