А.А.
Научный руководитель: проф., к.т.н. Авдошин С.М.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Новый подход к решению систем уравнений в задачах дискретного логарифмирования презентация
Содержание
- 1. Новый подход к решению систем уравнений в задачах дискретного логарифмирования
- 2. Криптографические системы, основанные на сложности дискретного логарифмирования
- 3. Алгоритмы дискретного логарифмирования в конечных полях, использующие
- 4. Постановка задачи Решить систему n линейных уравнений
- 5. Сведение задачи к : решению
- 6. Анализ методов решения систем линейных уравнений в
- 7. Метод сведения к решению системы над простыми
- 8. Метод сведения к решению системы над простыми полями: пример (продолжение) 1 2
- 9. Метод сведения к решению системы над простыми полями: пример (продолжение) 1 2 3
- 10. Метод сведения к решению системы над простыми полями: пример (продолжение) 3 2 1
- 11. Метод сведения к решению системы над простыми полями: пример (продолжение) По Китайской теореме об остатках:
- 12. Недостатки метода сведения к решению семейства систем
- 13. Анализ методов решения систем линейных уравнений в
- 14. Метод сведения к решению системы над кольцом
- 15. Метод сведения к решению системы над кольцом
- 16. Анализ методов решения систем линейных уравнений в
- 17. Метод сведения к уравнению над кольцом матриц
- 18. Предложенный метод В основе: Расширенный алгоритм Евклида
- 19. Расширенный алгоритм Евклида АЛГ Евклид(a,b)
- 20. Схема Жордана
- 21. Матрицы над кольцом Опр.2 Матрица
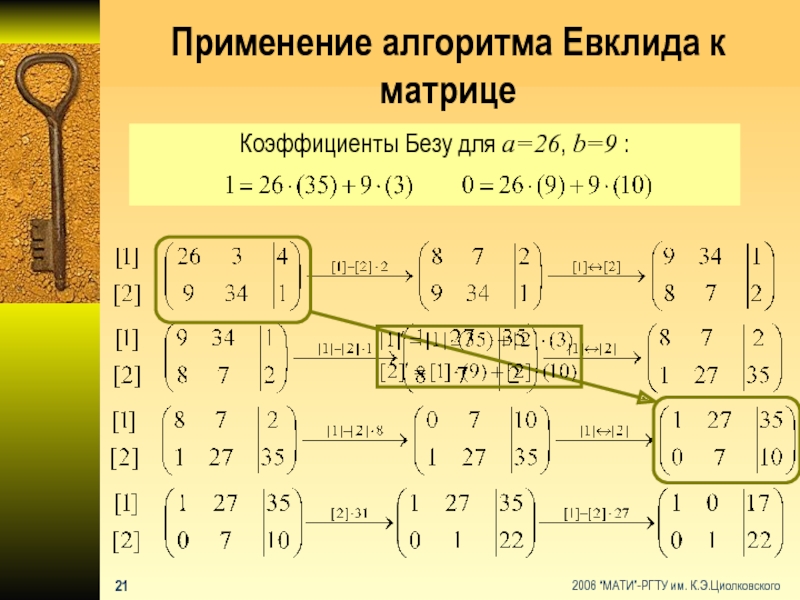
- 22. Применение алгоритма Евклида к матрице
- 23. Работа алгоритма Решение системы: Вычисление обратной матрицы:
- 24. Алгоритм АЛГ Жордан(А, n, m, p)
- 25. Алгоритм (продолжение) ЕСЛИ НОД(aii,
- 26. Временная сложность алгоритмов
- 27. Временная сложность алгоритмов
- 28. Временная сложность алгоритмов
- 29. Временная сложность алгоритмов
- 30. Временная сложность алгоритмов
- 31. Решение систем, возникающих при дискретном логарифмировании
- 32. Заключение Результаты, полученные в данной работе: Проведен
- 33. Направление дальнейшей работы Теоретическое и экспериментальное исследование
- 34. Кольца вычетов Операции сложения и умножения определяют
- 35. Обратный элемент Элемент
- 36. Пример решения системы в поле Галуа порядка 37
- 37. Пример решения системы в кольце вычетов по
Криптографические системы, основанные на сложности дискретного логарифмирования Схема открытого распределения ключей Диффи-Хеллмана Схема ЭЦП Эль-Гамаля ГОСТ Р34.10-2001(Россия) ANSI X9.62/63-2001 (США)
Слайд 1Новый подход к решению систем уравнений в задачах дискретного логарифмирования
Выполнила: Савельева
Слайд 2Криптографические системы, основанные на сложности дискретного логарифмирования
Схема открытого распределения ключей Диффи-Хеллмана
Схема
ЭЦП Эль-Гамаля
ГОСТ Р34.10-2001(Россия)
ANSI X9.62/63-2001 (США)
ГОСТ Р34.10-2001(Россия)
ANSI X9.62/63-2001 (США)
Слайд 3Алгоритмы дискретного логарифмирования в конечных полях, использующие факторную базу
Алгоритм Адлемана
Алгоритм COS
Index-calculus
Решето
числового поля
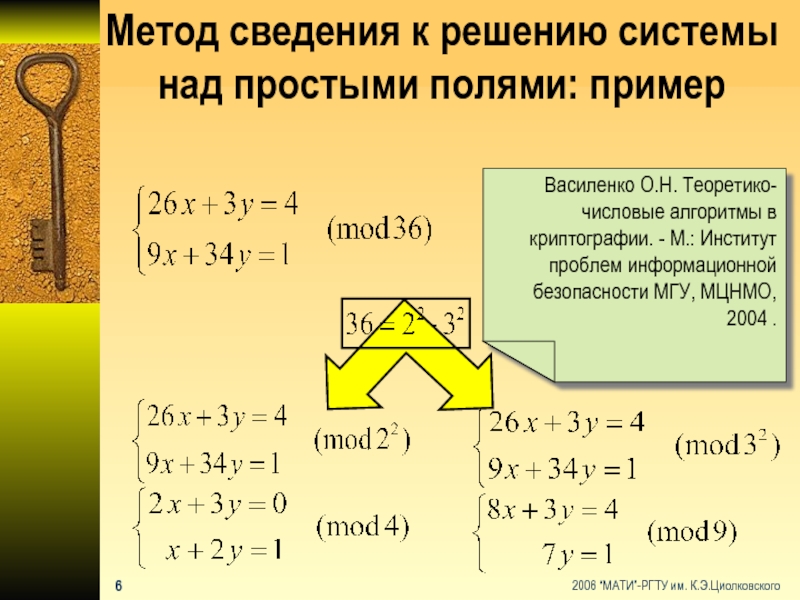
Василенко О.Н. Теоретико-числовые алгоритмы в криптографии. - М.: МЦНМО, 2004 .
Слайд 4Постановка задачи
Решить систему n линейных уравнений c m неизвестными:
Операции сложения и
умножения определены по правилам:
(здесь p - некоторое целое положительное число)
Слайд 5
Сведение задачи к :
решению семейства систем над полями Галуа
решению системы над
кольцом целых чисел
решению уравнения над кольцом матриц
решению уравнения над кольцом матриц
Анализ методов решения систем линейных уравнений в кольцах вычетов
Слайд 6Анализ методов решения систем линейных уравнений в кольцах вычетов
Сведение задачи к
:
решению семейства систем над простыми полями
решению системы над кольцом целых чисел
решению уравнения над кольцом матриц
решению семейства систем над простыми полями
решению системы над кольцом целых чисел
решению уравнения над кольцом матриц
Слайд 7Метод сведения к решению системы над простыми полями: пример
Василенко О.Н. Теоретико-числовые
алгоритмы в криптографии. - М.: Институт проблем информационной безопасности МГУ, МЦНМО, 2004 .
Слайд 11Метод сведения к решению системы над простыми полями: пример (продолжение)
По Китайской
теореме об остатках:
Слайд 12Недостатки метода сведения к решению семейства систем над простыми полями
Решение не
одной, а нескольких систем
Факторизация числа p: открытая проблема современной теории чисел (не существует алгоритма с полиномиальной сложностью)
Факторизация числа p: открытая проблема современной теории чисел (не существует алгоритма с полиномиальной сложностью)
Слайд 13Анализ методов решения систем линейных уравнений в кольцах вычетов
Сведение задачи к
:
решению семейства систем над простыми полями
решению системы над кольцом целых чисел
решению уравнения над кольцом матриц
решению семейства систем над простыми полями
решению системы над кольцом целых чисел
решению уравнения над кольцом матриц
Слайд 14Метод сведения к решению системы над кольцом целых чисел (1): пример
Сведение:
Общее
решение:
экспоненциальный рост коэффициентов
Ноден П., Китте К. Алгебраическая алгоритмика. Пер. с франц. - М.: Мир, 1999.
Слайд 15Метод сведения к решению системы над кольцом целых чисел (2): модификации
Способы
избежать экспоненциального роста коэффициентов:
Использование диагональной формы Смита
Модификация метода Гаусса
Недостаток:
Асимптотическая временная и емкостная сложность значительно больше сложности метода Жордана решения систем в полях Галуа
Использование диагональной формы Смита
Модификация метода Гаусса
Недостаток:
Асимптотическая временная и емкостная сложность значительно больше сложности метода Жордана решения систем в полях Галуа
Кузнецов М.И., Бурланков Д.Е., Чирков А.Ю., Яковлев В.А. Компьютерная алгебра: Учебник. - Нижегородский Государственный Университет им. Н.И. Лобачевского. – 2002.
Полиномиальный рост коэффициентов
Слайд 16Анализ методов решения систем линейных уравнений в кольцах вычетов
Сведение задачи к
:
решению семейства систем над простыми полями
решению системы над кольцом целых чисел
решению уравнения над кольцом матриц
решению семейства систем над простыми полями
решению системы над кольцом целых чисел
решению уравнения над кольцом матриц
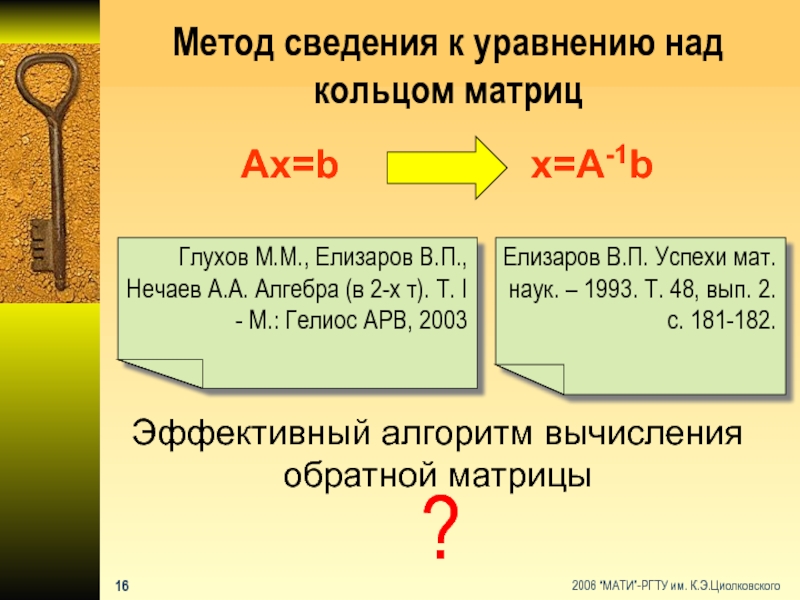
Слайд 17Метод сведения к уравнению над кольцом матриц
Ax=b
x=A-1b
Елизаров В.П. Успехи мат. наук.
– 1993. Т. 48, вып. 2. с. 181-182.
Глухов М.М., Елизаров В.П., Нечаев А.А. Алгебра (в 2-х т). Т. I - М.: Гелиос АРВ, 2003
Слайд 18Предложенный метод
В основе:
Расширенный алгоритм Евклида
Схема Жордана
Применим для:
колец вычетов
полей Галуа
Эффективность:
По временной и
емкостной сложности эквивалентен классическим алгоритмам Жордана и Гаусса решения систем в полях Галуа
Слайд 19Расширенный алгоритм Евклида
АЛГ Евклид(a,b)
ПОКА ЦИКЛ
К.Ц.
К.АЛГ.
К.Ц.
К.АЛГ.
Вход:
Выход: d, x, y, r, s такие, что
Слайд 21Матрицы над кольцом
Опр.2 Матрица
называется строчно эквивалентной матрице если она может быть получена из A с помощью конечной последовательности элементарных преобразований строк.
Элементарными преобразованиями строк матрицы называют:
умножение любой ее строки на обратимый элемент кольца R;
прибавление к любой ее строке другой строки, умноженной на произвольный элемент кольца R;
транспозицию строк.
Опр.1 Множество всех матриц размером m x n с элементами из кольца R будем обозначать через Rm,n
Слайд 24Алгоритм
АЛГ Жордан(А, n, m, p)
ДЛЯ i=1 ДО n
ЦИКЛ
{обнуляем эл-ты i-го столбца ниже i-й строки}
ДЛЯ j=i+1 ДО n ЦИКЛ
К.Ц. {для j}
{обнуляем эл-ты i-го столбца ниже i-й строки}
ДЛЯ j=i+1 ДО n ЦИКЛ
К.Ц. {для j}
Вход: {расширенная матрица}
Выход: А {преобразованная матрица}
Слайд 25Алгоритм (продолжение)
ЕСЛИ НОД(aii, p)>1
ТО выйти из алгоритма
{матрица вырождена}
ИНАЧЕ {обнуляем элементы i-го столбца выше i-й строки}
К.Е.
ВЕРНУТЬ(А)
К.АЛГ.
ИНАЧЕ {обнуляем элементы i-го столбца выше i-й строки}
К.Е.
ВЕРНУТЬ(А)
К.АЛГ.
Слайд 26Временная сложность алгоритмов
Кузнецов М.И., Бурланков Д.Е., Чирков А.Ю., Яковлев В.А. Компьютерная
алгебра: Учебник. - Нижегородский Государственный Университет им. Н.И. Лобачевского. – 2002.
Глухов М.М., Елизаров В.П., Нечаев А.А. Алгебра
(в 2-х т). Т. I - М.: Гелиос АРВ, 2003
Елизаров В.П. Успехи мат. наук.–1993.Т. 48, вып. 2.
Метод сведения к уравнению над кольцом матриц
Метод сведения к диофантовым уравнениям
(с построением матрицы Смита)
Метод сведения к полям Галуа
Метод, предложенный в данной работе
Василенко О.Н. Теоретико-числовые алгоритмы в криптографии. - М.: Институт проблем информационной безопасности МГУ,
МЦНМО, 2004
Авдошин С.М., Савельева А.А. Свид. Об официальной регистрации программы для ЭВМ № 2005612258: «Программа решения систем линейных уравнений в кольцах вычетов». Зарегистрировано в Реестре программ для ЭВМ 02.09.2005
Слайд 27Временная сложность алгоритмов
Авдошин С.М., Савельева А.А. Свид. Об официальной регистрации программы
для ЭВМ № 2005612258: «Программа решения систем линейных уравнений в кольцах вычетов». Зарегистрировано в Реестре программ для ЭВМ 02.09.2005
Кузнецов М.И., Бурланков Д.Е., Чирков А.Ю., Яковлев В.А. Компьютерная алгебра: Учебник. - Нижегородский Государственный Университет им. Н.И. Лобачевского. – 2002.
Глухов М.М., Елизаров В.П., Нечаев А.А. Алгебра
(в 2-х т). Т. I - М.: Гелиос АРВ, 2003
Елизаров В.П. Успехи мат. наук.–1993.Т. 48, вып. 2.
Метод сведения к уравнению над кольцом матриц
Метод сведения к диофантовым уравнениям
(с построением матрицы Смита)
Метод сведения к полям Галуа
Метод, предложенный в данной работе
Слайд 28Временная сложность алгоритмов
Авдошин С.М., Савельева А.А. Свид. Об официальной регистрации программы
для ЭВМ № 2005612258: «Программа решения систем линейных уравнений в кольцах вычетов». Зарегистрировано в Реестре программ для ЭВМ 02.09.2005
Глухов М.М., Елизаров В.П., Нечаев А.А. Алгебра
(в 2-х т). Т. I - М.: Гелиос АРВ, 2003
Елизаров В.П. Успехи мат. наук.–1993.Т. 48, вып. 2.
Метод сведения к уравнению над кольцом матриц
Метод сведения к диофантовым уравнениям
(с построением матрицы Смита)
Метод сведения к полям Галуа
Метод, предложенный в данной работе
Слайд 29Временная сложность алгоритмов
Авдошин С.М., Савельева А.А. Свид. Об официальной регистрации программы
для ЭВМ № 2005612258: «Программа решения систем линейных уравнений в кольцах вычетов». Зарегистрировано в Реестре программ для ЭВМ 02.09.2005
Метод сведения к уравнению над кольцом матриц
Метод сведения к диофантовым уравнениям
(с построением матрицы Смита)
Метод сведения к полям Галуа
Метод, предложенный в данной работе
Слайд 30Временная сложность алгоритмов
Метод сведения к уравнению над кольцом матриц
Метод сведения к
диофантовым уравнениям
(с построением матрицы Смита)
Метод сведения к полям Галуа
Метод, предложенный в данной работе
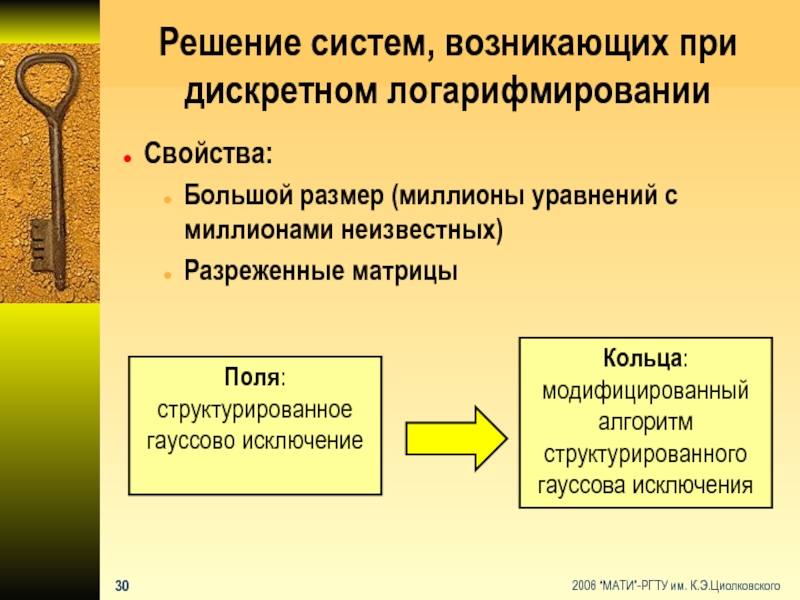
Слайд 31Решение систем, возникающих при дискретном логарифмировании
Свойства:
Большой размер (миллионы уравнений с
миллионами неизвестных)
Разреженные матрицы
Разреженные матрицы
Поля: структурированное гауссово исключение
Кольца: модифицированный алгоритм структурированного гауссова исключения
Слайд 32Заключение
Результаты, полученные в данной работе:
Проведен анализ известных методов решения систем линейных
уравнений над кольцом вычетов
Разработан алгоритм, эквивалентный по сложности методам Жордана и Гаусса решения систем линейных уравнений над полями Галуа
Программа, реализующая разработанный алгоритм, зарегистрирована Федеральной службой по интеллектуальной собственности, патентам и товарным знакам (Роспатент)
Результаты исследований опубликованы в журнале «Информационные технологии» (№2, 2006)
Разработан алгоритм, эквивалентный по сложности методам Жордана и Гаусса решения систем линейных уравнений над полями Галуа
Программа, реализующая разработанный алгоритм, зарегистрирована Федеральной службой по интеллектуальной собственности, патентам и товарным знакам (Роспатент)
Результаты исследований опубликованы в журнале «Информационные технологии» (№2, 2006)
Слайд 33Направление дальнейшей работы
Теоретическое и экспериментальное исследование влияния полученного метода на временную
сложность алгоритмов дискретного логарифмирования, использующие факторную базу:
Алгоритм Адлемана
Index-calculus
Алгоритм COS
Решето числового поля
Алгоритм Адлемана
Index-calculus
Алгоритм COS
Решето числового поля
Слайд 34Кольца вычетов
Операции сложения и умножения определяют кольцо вычетов по модулю p
. Оно является коммутативным кольцом с единицей.
Опр.1 Делителем нуля в произвольном кольце R называется любой его элемент для которого в R существует элемент удовлетворяющий условию a ·b=0 или b ·a=0
Опр.2 Обратимым элементом в произвольном кольце R называется любой его элемент для которого в R существует обратный элемент a-1, удовлетворяющий условию a · a-1 =1 или a-1 ·a=1
Опр.1 Делителем нуля в произвольном кольце R называется любой его элемент для которого в R существует элемент удовлетворяющий условию a ·b=0 или b ·a=0
Опр.2 Обратимым элементом в произвольном кольце R называется любой его элемент для которого в R существует обратный элемент a-1, удовлетворяющий условию a · a-1 =1 или a-1 ·a=1
Слайд 35Обратный элемент
Элемент
называется обратным к , если
Для нахождения обратного элемента нужно решить линейное диофантово уравнение:
Уравнение разрешимо относительно u и v тогда и только тогда, когда НОД(x,p)=1; в этом случае Для вычисления u и v (коэффициентов Безу) используется расширенный алгоритм Евклида.
Слайд 37Пример решения системы в кольце вычетов по модулю 36
Все коэффициенты системы
являются делителями нуля, т.е. необратимы. Однако решение существует и единственно:
