- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Мультиплексоры и демультиплексоры презентация
Содержание
- 1. Мультиплексоры и демультиплексоры
- 2. Мультиплексоры осуществляют подключение одного
- 3. Мультиплексоры Каждому информационному входу
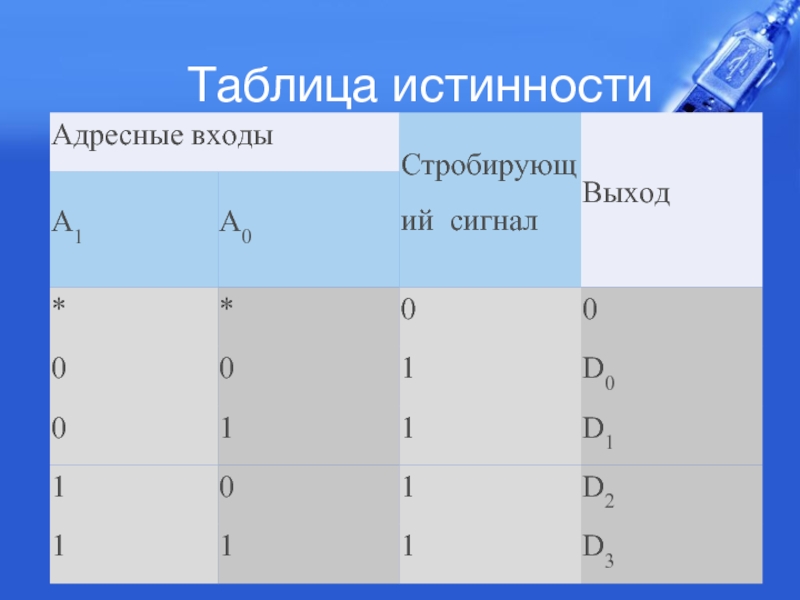
- 5. Таблица истинности
- 6. Рисунок
- 7. Работа мультиплексора описывается соотношением:
- 8. Универсальные логические модули на основе мультиплексоров
- 9. Схема использования мультиплексора в качестве
- 10. На схеме а - иллюстрирует возможность воспроизведения
- 11. Второй способ настройки УЛМ Большее число входов
- 12. Демультиплексоры
- 13. называются устройства, которые позволяют подключать один вход к нескольким выходам. Демультиплексорами
- 14. Демультиплексор можно построить на основе точно таких
- 15. В этой схеме для выбора конкретного выхода
- 16. Если рассмотреть принципиальную схему самого дешифратора, то
- 17. Условно графическое обозначение демультиплексора с четырьмя выходами.
- 18. В МОП микросхемах не существует отдельных микросхем
- 19. Компараторы
- 20. Компараторы (устройства сравнения)
- 21. Рисунок 8.4 Условное обозначение компаратора с тремя выходами
- 22. Устройства сравнения на равенство строятся на основе
- 23. Признак неравенства разрядов Признак равенства
- 24. Рисунок 8.5 Схема компаратора на равенство
- 25. Подобный же подход справедлив и для слов
Слайд 2Мультиплексоры
осуществляют подключение одного из входных каналов к выходному под управлением управляющего
Слайд 3Мультиплексоры
Каждому информационному входу мультиплексора присваивается номер, называемый адресом. При подаче стробирующего
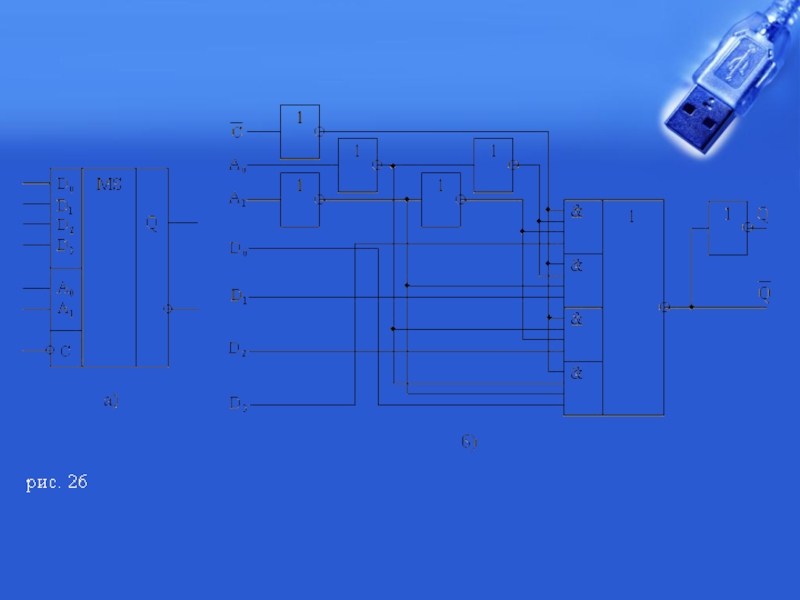
Слайд 6
Рисунок 8.1 Упрощенное представление мультиплексора многопозиционным ключом
Адресующий код А
2n-1
Слайд 7Работа мультиплексора описывается соотношением:
которое иногда называется мультиплексной формулой. При
Слайд 8 Универсальные логические модули на основе мультиплексоров
Универсальные логические модули (УЛМ)
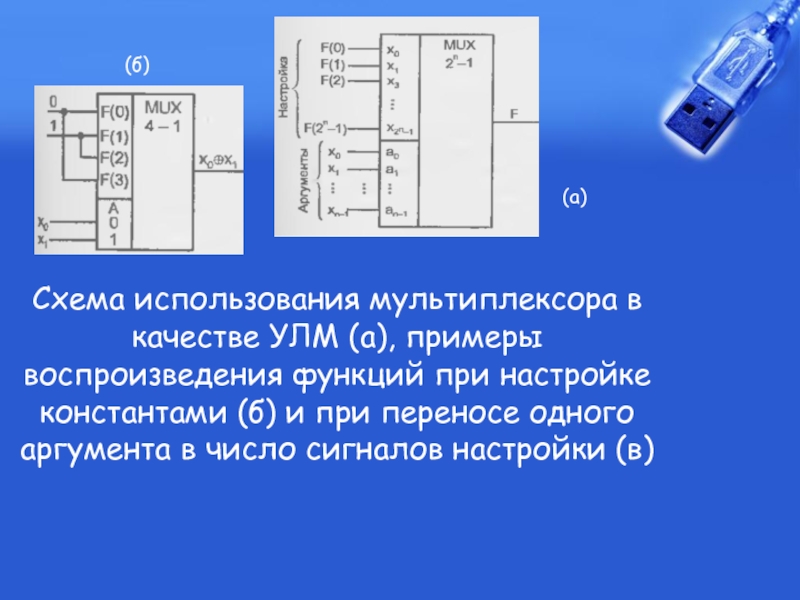
Слайд 9
Схема использования мультиплексора в качестве УЛМ (а), примеры воспроизведения функций
(а)
(б)
х2 с помощью мультиплексора "4—1".
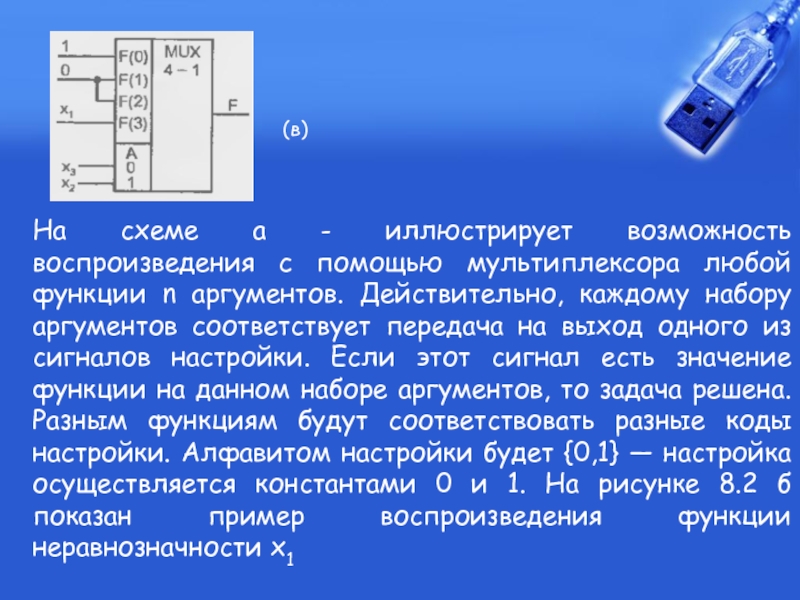
Слайд 10На схеме а - иллюстрирует возможность воспроизведения с помощью мультиплексора любой
(в)
Слайд 11Второй способ настройки УЛМ
Большее число входов настройки наталкивает на поиск возможностей
Логический блок выработки сигналов настройки УЛМ с переносом двух аргументов в сигналы настройки (а) и пример схемы воспроизведения функции четырех аргументов на мультиплексоре "4—1" (б)
(а)
(б)
Слайд 13
называются устройства, которые позволяют подключать один вход к нескольким выходам.
Демультиплексорами
Слайд 14Демультиплексор можно построить на основе точно таких же схем логического "И",
Существенным отличием от мультиплексора является возможность объединения нескольких входов в один без дополнительных схем.
Однако для увеличения нагрузочной способности микросхемы, на входе демультиплексора для усиления входного сигнала лучше поставить инвертор.
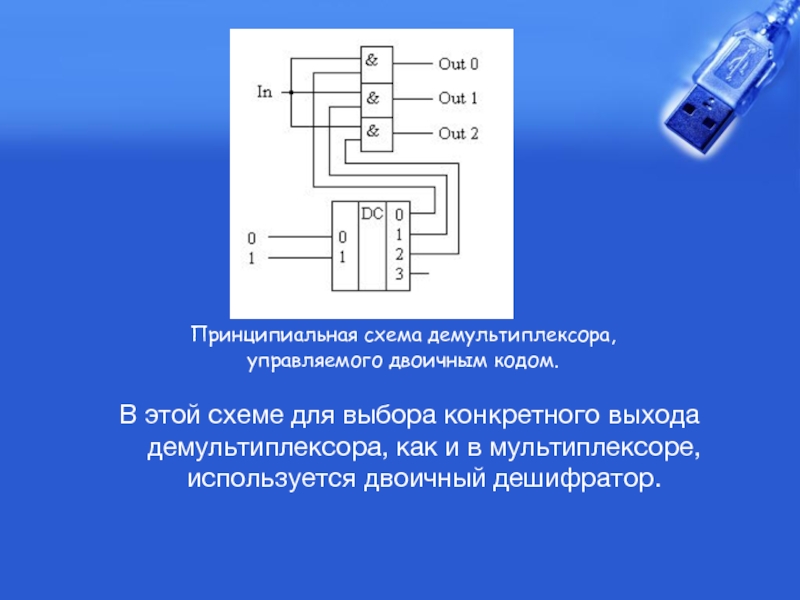
Слайд 15В этой схеме для выбора конкретного выхода демультиплексора, как и в
Принципиальная схема демультиплексора,
управляемого двоичным кодом.
Слайд 16Если рассмотреть принципиальную схему самого дешифратора, то можно значительно упростить демультиплексор.
Достаточно просто к каждому логическому элементу 'И', входящему в состав дешифратора просто добавить ещё один вход – In.
Такую схему часто называют дешифратором с входом разрешения работы. Условно-графическое изображение демультиплексора приведено на следущем рисунке.
Слайд 17Условно графическое обозначение демультиплексора с четырьмя выходами.
В этом обозначении вход In
Слайд 18В МОП микросхемах не существует отдельных микросхем демультиплексоров, так как МОП
Слайд 20
Компараторы
(устройства сравнения)
определяют отношения между двумя словами. Основными отношениями,
Слайд 22Устройства сравнения на равенство строятся на основе поразрядных операций над одноименными
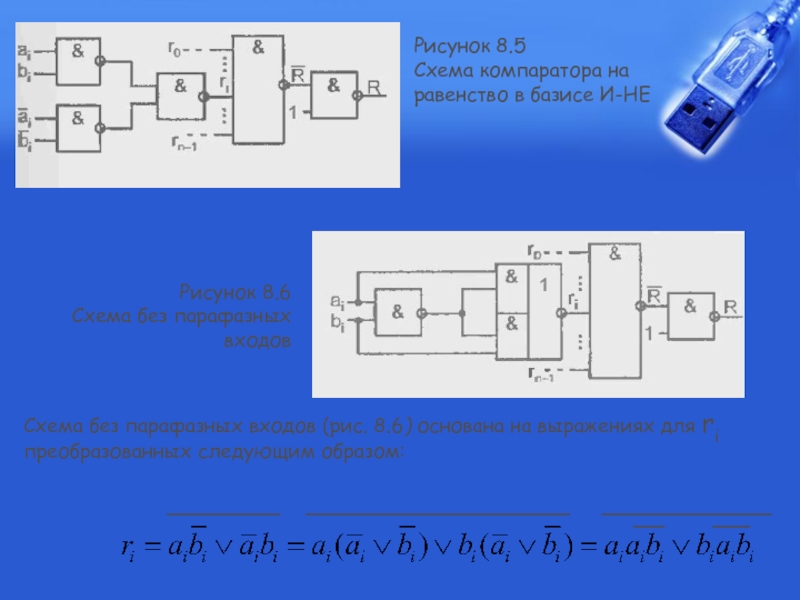
Слайд 24Рисунок 8.5
Схема компаратора на равенство в базисе И-НЕ
Рисунок 8.6
Схема без парафазных входов
Схема без парафазных входов (рис. 8.6) основана на выражениях для ri преобразованных следующим образом:
Слайд 25Подобный же подход справедлив и для слов любой разрядности — к
Таким образом, для общего случая n-разрядных слов имеем