- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Московская область, Ленинский районМОУ Коммунарский лицей презентация
Содержание
- 1. Московская область, Ленинский районМОУ Коммунарский лицей
- 2. Проектная работа на тему «В
- 3. Цели проектной работы: Рассмотреть понятие
- 4. Введение Знаете ли вы, что эта обыкновенная,
- 5. Проблеме π – 4000 лет. Исследователи древних
- 6. Что за число такое? Пи обратило
- 7. История числа ПИ История числа Пи, выражающего
- 8. Франсуа Виет нашёл число Пи только с
- 9. Лудольф ван Цейлен (1540-1610) нашёл 32 правильных знака
- 10. Число Пи тысячи лет считалось мистическим, древние
- 11. Для чего надо знать точное значение числа
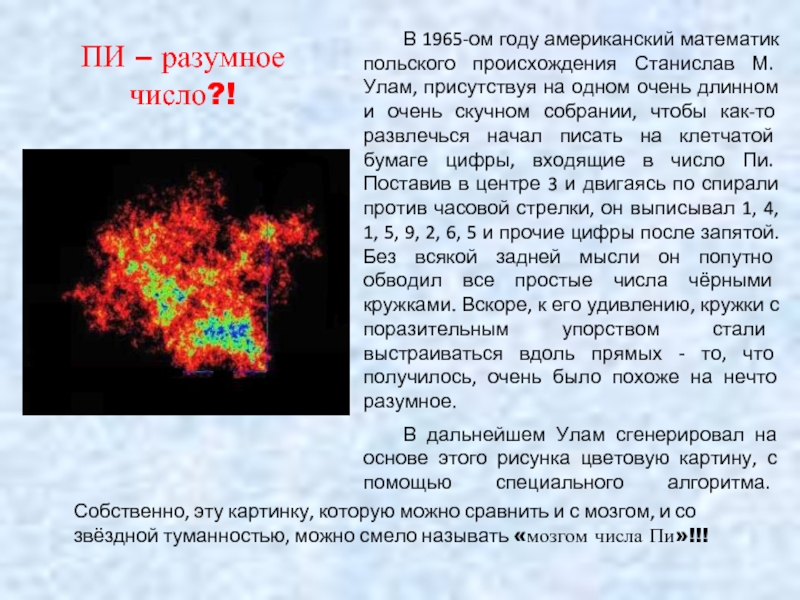
- 12. ПИ – разумное число?!
- 13. Осмысленные круги на полях? Один из
- 14. Как считает доктор Чарльз Кэнтор, под руководством
- 15. Международный день числа пи
- 16. Есть ли закономерность числа пи? Математики пытались
- 17. На следующем слайде мы увидим только первые 100000 знаков числа "пи".
- 18. 3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072602491412737245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094330572703657595919530921861173819326117931051185480744623799627495673518857527248912279381830119491298336733624406566430860213949463952247371907021798609437027705392171762931767523846781846766940513200056812714526356082778577134275778960917363717872146844090122495343014654958537105079227968925892354201995611212902196086403441815981362977477130996051870721134999999837297804995105973173281609631859502445945534690830264252230825334468503526193118817101000313783875288658753320838142061717766914730359825349042875546873115956286388235378759375195778185778053217122680661!30019278766111959092164201989380952572010654858632788659361533818279682303019520353018529689957736225994138912497217752834791315155748572424541506959508295331168617278558890750983817546374649393192550604009770167113900984882401285836160356370766010471018194295559619894676783744944825537977472684710404753464620804668425906949129331367702898915210475216205696602405803815019351125338243003558764024749647326391419927260426992279678235478163600934172164121992458631503028618297455570674983850549458858692449872027559602364806654991198818347977535663698074265425278625518184175746728909777727938000816470600161452491921732172147723501414419735685481613611573525521334757418494684385233239073941433345477624168625189835694855620992192221842725502542568876717904946016534668049886272327917860857843838279679766814541009538837863609506800642251252051173929489608412848862694560424196528502221066118630674427862203919494504712371378696095636437!191728746776465757396241389086583264599581339047802759009946576407895126946839835259570982582262052248940772671947826848260147699090264013639443745530506820349625245174939965143142980919065925093722169646151570985838741059788595977297549893016175392846813826868386894277415599185592524595395943104997252468084598727364469584865383673622262609912460805124388439045124413654976278079771569143599770012961608944169486855584840635342207222582848864815845602850601684273945226746767889525213852254995466672782398645659611635488623057745649803559363456817432411251507606947945109659609402522887971089314566913686722874894056010150330861792868092087476091782493858900971490967598526136554978189312978482168299894872265880485756401427047755513237964145152374623436454285844479526586782105114135473573952311342716610213596953623144295248493718711014576540359027993440374200731057853906219838744780847848968332144571386875194350643021845319104848100537061468067491927819119793995206!141966342875444064374512371819217999839101591956181467514269123974894090718649423196156794520809514655022523160388193014209376213785595663893778708303906979207734672218256259966150142150306803844773454920260541466592520149744285073251866600213243408819071048633173464965145390579626856100550810665879699816357473638405257145910289706414011097120628043903975951567715770042033786993600723055876317635942187312514712053292819182618612586732157919841484882916447060957527069572209175671167229109816909152801735067127485832228718352093539657251210835791513698820914442100675103346711031412671113699086585163983150197016515116851714376576183515565088490998985998238734552833163550764791853589322618548963213293308985706420467525907091548141654985946163718027098199430992448895757128289059232332609729971208443357326548938239119325974636673058360414281388303203824903758985243744170291327656180937734440307074692112019130203303801976211011004492932151608424448596376698389522868478312355265821314495768572643344189303968642624341077322697802807318915441101044682325271620105265227211166039666557309254711055785376346682065310989652691862056476931257058635662018558100729360659876486117910453348850346113657867532494416680396265797877185560845529654126654085306143444318586769751456614068007002378776591344017127494704205622305389945613140711270004078547332699390814546646458807972708266830634328587856983052358089330657574067954571637752542021149557615814002501262285941302164715509792592309907965473761255176567513575178296664547791745011299614890304639947132962107340437518957359614589019389713111790429782856475032031986915140287080859904801094121472213179476477726224142548545403321571853061422881585043063321751829798662237172159160771669254748738986654949450114654062843366393790039769265672146385306736096571209180763832716641627488880078692560290228472104031721186082041900042296617119637792133757511495950156604963186294726547364252308177!036751590673502350728354056704038674351362222477158915049530984448933309634087807693259939780541934144737744184263129860809988868741326047215695162396586457302163159819319516735381297416772947867242292465436680098067692823828068996400482435403701416314965897940924323789690706977942236250822168895738379862300159377647165122893578601588161755782973523344604281512627203734314653197777416031990665541876397929334419521541341899485444734567383162499341913181480927777103863877343177207545654532207770921201905166096280490926360197598828161332316663652861932668633606273567630354477628035045077723554710585954870279081435624014517180624643626794561275318134078330336254232783944975382437205835311477119926063813346776879695970309833913077109870408591337464144282277263465947047458784778720192771528073176790770715721344473060570073349243693113835049316312840425121925651798069411352801314701304781643788518529092854520116583934196562134914341595625865865570552690496520985803!38507224264829397285847831630577775606888764462482468579260395352773480304802900587607582510474709164396136267604492562742042083208566119062545433721315359584506877246029016187667952406163425225771954291629919306455377991403734043287526288896399587947572917464263574552540790914513571113694109119393251910760208252026187985318877058429725916778131496990090192116971737278476847268608490033770242429165130050051683233643503895170298939223345172201381280696501178440874519601212285993716231301711444846409038906449544400619869075485160263275052983491874078668088183385102283345085048608250393021332197155184306354550076682829493041377655279397517546139539846833936383047461199665385815384205685338621867252334028308711232827892125077126294632295639898989358211674562701021835646220349671518819097303811980049734072396103685406643193950979019069963955245300545058068550195673022921913933918568034490398205955100226353536192041994745538593810234395544959778377902374216172711!172364343543947822181852862408514006660443325888569867054315470696574745855033232334210730154594051655379068662733379958511562578432298827372319898757141595781119635833005940873068121602876496286744604774649159950549737425626901049037781986835938146574126804925648798556145372347867330390468838343634655379498641927056387293174872332083760112302991136793862708943879936201629515413371424892830722012690147546684765357616477379467520049075715552781965362132392640616013635815590742202020318727760527721900556148425551879253034351398442532234157623361064250639049750086562710953591946589751413103482276930624743536325691607815478181152843667957061108615331504452127473924544945423682886061340841486377670096120715124914043027253860764823634143346235189757664521641376796903149501910857598442391986291642193994907236234646844117394032659184044378051333894525742399508296591228508555821572503107125701266830240292952522011872676756220415420516184163484756516999811614101002996!0783869092916030288400269104140792886215078424516709087000699282120660418371806535567252532567532861291042487761825829765157959847035622262934860034158722980534989650226291748788202734209222245339856264766914905562842503912757710284027998066365825488926488025456610172967026640765590429099456815065265305371829412703369313785178609040708667114965583434347693385781711386455873678123014587687126603489139095620099393610310291616152881384379099042317473363948045759314931405297634757481193567091101377517210080315590248530906692037671922033229094334676851422144773793937517034436619910403375111735471918550464490263655128162288244625759163330391072253837421821408835086573917715096828874782656995995744906617583441375223970968340800535598491754173818839994469748676265516582765848358845314277568790029095170283529716344562129640435231176006651012412006597558512761785838292041974844236080071930457618932349229279650198751872127267507981255470958904556357921221033346697499235!63025494780249011419521238281530911407907386025152274299581807247162591668545133312394804947079119153267343028244186041426363954800044800267049624820179289647669758318327131425170296923488962766844032326092752496035799646925650493681836090032380929345958897069536534940603402166544375589004563288225054525564056448246515187547119621844396582533754388569094113031509526179378002974120766514793942590298969594699556576121865619673378623625612521632086286922210327488918654364802296780705765
- 19. Вывод Число Пи является удивительным
Слайд 2
Проектная работа на тему
«В чем леденящая тайна числа ПИ?»
Номинация: «История
Работу выполнили:
Бяхова Дарья Алексеевна,
Кобзева Елизавета Анатольевна
Руководитель проекта:
Фокина Наталья Александровна, учитель математики
Слайд 3
Цели проектной работы:
Рассмотреть понятие числа Пи;
Ознакомится с историей возникновения числа Пи;
Выяснить
Слайд 4Введение
Знаете ли вы, что эта обыкновенная, на первый взгляд, полузабытая буква
А может это код Мироздания?
Слайд 5 Проблеме π – 4000 лет. Исследователи древних пирамид установили, что частное,
Слайд 6 Что за число такое?
Пи обратило на себя внимание людей ещё
умов не было предела: оказалось, что число три весьма неточно выражает это соотношение. С течением времени и развитием наук это
число стали полагать равным двадцати двум седьмым.
Слайд 7История числа ПИ
История числа Пи, выражающего отношение длины окружности к её
В то время число Пи считали равным дроби 16/9 в квадрате, или 256/81, т.е Пи = 3,160...
В священной книге джайнизма имеется указание, что число Пи в то время принимали равным, корню квадратному из десяти, что даёт дробь 3,162... Древние греки Евдокс, Гиппократ и другие измерение окружности сводили к построению отрезка, а измерение круга - к построению равновеликого квадрата.
На протяжении многих столетий математики разных стран и народов пытались выразить отношение длины окружности к диаметру рациональным числом. Всем известный Архимед ещё уточнил значение числа Пи. По точным расчётам Архимеда Пи = 3,1419... Истинное значение этого отношения 3,1415922653...
В V в. до н.э. китайским математиком Цзу Чунчжи было найдено более точное значение этого числа: 3,1415927...
В первой половине XV в обсерватории Улугбека, возле Самарканда, астроном и математик ал-Каши вычислил Пи с 16 десятичными знаками.
Слайд 8Франсуа Виет нашёл число Пи только с 9 правильными десятичными знаками,
В конце XVIII в. А.М. Лажандр на основе
работ И.Г.Ламберта доказал, что число Пи
иррационально. Немецкий математик
Ф. Линдеман, нашёл строгое доказательство
того, что число Пи не только иррационально,
но и трансцендентно, т.е. не может быть корнем
алгебраического уравнения. Из этого следует,
что с помощью только циркуля и линейки
построить отрезок, равный по длине окружности,
н е в о з м о ж н о.
Слайд 9Лудольф ван Цейлен (1540-1610) нашёл 32 правильных знака Пи. Число Пи с
Со временем труд вычислителей заменили
ЭВМ. С помощью ЭВМ число Пи было
вычислено с точностью более миллиона
знаков после запятой. В современной
математике число Пи - это не только
отношение длины окружности к диаметру.
Оно Входит в большое число
различных формул, в том числе и
в формулы неевклидовой геометрии, и
формулу Л.Эйлера.
Слайд 10Число Пи тысячи лет считалось мистическим, древние греки даже построили на
В конце 18 века Ламберт и Лежандр установили, что Пи - иррациональное число, т.е. его нельзя представить отношением p/q, где q≠0 и p, q - натуральные числа.
Вычисления числа Пи имеют не только прикладное значение. Так, в настоящее время с Пи связано множество нерешенных задач. Например, до сих пор не доказана нормальность числа Пи, т.е. встречаются ли в нем все цифры от 0 до 9 одинаково часто, или какая-то цифра встречается чаще, чем другие.
Число Пи одна из фундаментальных математических констант. Оно встречается во многих уравнениях различных направлений науки, например, в уравнениях гравитационного поля Эйнштейна, в уравнениях, связанных с образованием радуги, в уравнениях описывающих распространение зыби при падении дождевой капли в воду, в уравнении движения маятника, во многих геометрических задачах, в задачах связанных с волнами, в задачах навигации и т.д.
Является ли разложение Пи случайным
или упорядоченным –
это одна из труднейших проблем
математики.
Бэйли и Крандалл показали, что нормальность
«пи» будет строго установлена, если удастся доказать
теорему из совсем другой области - теории хаоса.
Слайд 11Для чего надо знать точное значение числа Пи?
Неутомимые ученые продолжали и
Ученые Токийского университета сумели поставить мировой рекорд в вычислениях числа Пи до 12411-триллионного знака. Зачем же они это делают?
во-первых: для очень точных
вычислений какой-нибудь орбиты
спутника желательно иметь этих
знаков побольше;
во-вторых : огромное прикладное
значение: для строительства плотин
и гигантских мостов тоже
нужна точность;
и в главных: Пи - одна из наиболее универсальных и фундаментальных констант, известных Человечеству. Пи входит в формулы, описывающие движение космических кораблей и небесных тел в астрономии и в формулы для вычислений электронных орбит в квантовой физике и квантовой химии.
Слайд 12
ПИ – разумное
число?!
В 1965-ом году американский математик польского происхождения Станислав М.
В дальнейшем Улам сгенерировал на основе этого рисунка цветовую картину, с помощью специального алгоритма.
Собственно, эту картинку, которую можно сравнить и с мозгом, и со звёздной туманностью, можно смело называть «мозгом числа Пи»!!!
Слайд 13Осмысленные круги на полях?
Один из восьми «узоров» обнаруженных на полях Великобритании,
Астрофизик из Северной Каролины Майкл Рид увидел в узоре зашифрованное число пи! Майкл условно разделил круг на 10 секторов и обнаружил, что после дуги, обозначенной цифрой 3, стоит «точка», а сама дуга охватывает
три сектора. Значит, можно записать: 3 с запятой. Следующий отрезок дуги, обозначенный цифрой 1, занимает один сектор, следовательно, пишем 3,1, после чего охватываем дугу, занимающую четыре сектора. Пишем 3,14, а это уже число,
употребляемое в простых приблизительных расчетах! За дугой из четырех секторов
оказалась дуга в один сектор, затем в пять, девять, два и так далее. В результате получилось
число 3,141592654 – число Пи до девятого знака!
Слайд 14Как считает доктор Чарльз Кэнтор, под руководством которого было расшифровано ДНК:
Число Пи управляет нашим миром!
Если зашифровать все буквы цифрами, то в десятичном разложении числа пи можно найти всю мировую литературу и науку - это строгий научный факт. Ведь последовательность БЕСКОНЕЧНА и сочетания не повторяются, следовательно она содержит все сочетания цифр, и это уже доказано.Разве это может не волновать? Получается, что это число - единственное разумное число во вселенной! И ОНО управляет нашим миром. Но – каким образом происходит это управление?
Как правило, с помощью как познанных, так и еще не познанных и не написанных законов физики, химии, физиологии, астрономии, которые в нем содержатся! Это универсум в цифровом виде!
Слайд 15Международный день числа пи
В мире даже существует праздник—
Ученые считают, что - это число было открыто вавилонскими магами. Число «Пи» использовалось при строительстве Вавилонской башни. Однако, недостаточно точное исчисление значения «Пи» привело к краху всего проекта. Возможно, что эта математическая константа лежала в основе строительства легендарного Храма царя Соломона. Ученые очень любят этот праздник.
Слайд 16Есть ли закономерность числа пи?
Математики пытались всеми силами найти закономерность в
Вероятность встретить серию из семи троек в любом наугад выбранном месте десятичного разложения числа pi очень мала: шансы не встретить ее составляют 9999995 против 1. То, что такая серия троек встречается среди первых 710106 знаков после запятой в десятичном разложении pi, на первый взгляд кажется удивительным. Но если мы займемся поиском в том же разложении серий из идущих подряд семерок, то окажется, что они встречаются с большей вероятностью, чем серии из троек. Не менее удивительно, что с ненулевой вероятностью в десятичном разложении числа pi можно встретить и такие серии, как 4444444, 8888888, 1212121, 1234567 или 7654321. Поскольку заранее не известно, какую именно закономерность мы ищем, какую-нибудь серию нам удастся найти с ненулевой вероятностью. Единственное, от чего зависит успех, -- наша изобретательность в поиске скрытых закономерностей. Как некогда сказал Аристотель, невероятно то, что особенно вероятно.
Слайд 18
3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072602491412737245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094330572703657595919530921861173819326117931051185480744623799627495673518857527248912279381830119491298336733624406566430860213949463952247371907021798609437027705392171762931767523846781846766940513200056812714526356082778577134275778960917363717872146844090122495343014654958537105079227968925892354201995611212902196086403441815981362977477130996051870721134999999837297804995105973173281609631859502445945534690830264252230825334468503526193118817101000313783875288658753320838142061717766914730359825349042875546873115956286388235378759375195778185778053217122680661!30019278766111959092164201989380952572010654858632788659361533818279682303019520353018529689957736225994138912497217752834791315155748572424541506959508295331168617278558890750983817546374649393192550604009770167113900984882401285836160356370766010471018194295559619894676783744944825537977472684710404753464620804668425906949129331367702898915210475216205696602405803815019351125338243003558764024749647326391419927260426992279678235478163600934172164121992458631503028618297455570674983850549458858692449872027559602364806654991198818347977535663698074265425278625518184175746728909777727938000816470600161452491921732172147723501414419735685481613611573525521334757418494684385233239073941433345477624168625189835694855620992192221842725502542568876717904946016534668049886272327917860857843838279679766814541009538837863609506800642251252051173929489608412848862694560424196528502221066118630674427862203919494504712371378696095636437!191728746776465757396241389086583264599581339047802759009946576407895126946839835259570982582262052248940772671947826848260147699090264013639443745530506820349625245174939965143142980919065925093722169646151570985838741059788595977297549893016175392846813826868386894277415599185592524595395943104997252468084598727364469584865383673622262609912460805124388439045124413654976278079771569143599770012961608944169486855584840635342207222582848864815845602850601684273945226746767889525213852254995466672782398645659611635488623057745649803559363456817432411251507606947945109659609402522887971089314566913686722874894056010150330861792868092087476091782493858900971490967598526136554978189312978482168299894872265880485756401427047755513237964145152374623436454285844479526586782105114135473573952311342716610213596953623144295248493718711014576540359027993440374200731057853906219838744780847848968332144571386875194350643021845319104848100537061468067491927819119793995206!141966342875444064374512371819217999839101591956181467514269123974894090718649423196156794520809514655022523160388193014209376213785595663893778708303906979207734672218256259966150142150306803844773454920260541466592520149744285073251866600213243408819071048633173464965145390579626856100550810665879699816357473638405257145910289706414011097120628043903975951567715770042033786993600723055876317635942187312514712053292819182618612586732157919841484882916447060957527069572209175671167229109816909152801735067127485832228718352093539657251210835791513698820914442100675103346711031412671113699086585163983150197016515116851714376576183515565088490998985998238734552833163550764791853589322618548963213293308985706420467525907091548141654985946163718027098199430992448895757128289059232332609729971208443357326548938239119325974636673058360414281388303203824903758985243744170291327656180937734440307074692112019130203303801976211011004492932151608424448596376698389522868478312355265821314495768572643344189303968642624341077322697802807318915441101044682325271620105265227211166039666557309254711055785376346682065310989652691862056476931257058635662018558100729360659876486117910453348850346113657867532494416680396265797877185560845529654126654085306143444318586769751456614068007002378776591344017127494704205622305389945613140711270004078547332699390814546646458807972708266830634328587856983052358089330657574067954571637752542021149557615814002501262285941302164715509792592309907965473761255176567513575178296664547791745011299614890304639947132962107340437518957359614589019389713111790429782856475032031986915140287080859904801094121472213179476477726224142548545403321571853061422881585043063321751829798662237172159160771669254748738986654949450114654062843366393790039769265672146385306736096571209180763832716641627488880078692560290228472104031721186082041900042296617119637792133757511495950156604963186294726547364252308177!036751590673502350728354056704038674351362222477158915049530984448933309634087807693259939780541934144737744184263129860809988868741326047215695162396586457302163159819319516735381297416772947867242292465436680098067692823828068996400482435403701416314965897940924323789690706977942236250822168895738379862300159377647165122893578601588161755782973523344604281512627203734314653197777416031990665541876397929334419521541341899485444734567383162499341913181480927777103863877343177207545654532207770921201905166096280490926360197598828161332316663652861932668633606273567630354477628035045077723554710585954870279081435624014517180624643626794561275318134078330336254232783944975382437205835311477119926063813346776879695970309833913077109870408591337464144282277263465947047458784778720192771528073176790770715721344473060570073349243693113835049316312840425121925651798069411352801314701304781643788518529092854520116583934196562134914341595625865865570552690496520985803!38507224264829397285847831630577775606888764462482468579260395352773480304802900587607582510474709164396136267604492562742042083208566119062545433721315359584506877246029016187667952406163425225771954291629919306455377991403734043287526288896399587947572917464263574552540790914513571113694109119393251910760208252026187985318877058429725916778131496990090192116971737278476847268608490033770242429165130050051683233643503895170298939223345172201381280696501178440874519601212285993716231301711444846409038906449544400619869075485160263275052983491874078668088183385102283345085048608250393021332197155184306354550076682829493041377655279397517546139539846833936383047461199665385815384205685338621867252334028308711232827892125077126294632295639898989358211674562701021835646220349671518819097303811980049734072396103685406643193950979019069963955245300545058068550195673022921913933918568034490398205955100226353536192041994745538593810234395544959778377902374216172711!172364343543947822181852862408514006660443325888569867054315470696574745855033232334210730154594051655379068662733379958511562578432298827372319898757141595781119635833005940873068121602876496286744604774649159950549737425626901049037781986835938146574126804925648798556145372347867330390468838343634655379498641927056387293174872332083760112302991136793862708943879936201629515413371424892830722012690147546684765357616477379467520049075715552781965362132392640616013635815590742202020318727760527721900556148425551879253034351398442532234157623361064250639049750086562710953591946589751413103482276930624743536325691607815478181152843667957061108615331504452127473924544945423682886061340841486377670096120715124914043027253860764823634143346235189757664521641376796903149501910857598442391986291642193994907236234646844117394032659184044378051333894525742399508296591228508555821572503107125701266830240292952522011872676756220415420516184163484756516999811614101002996!0783869092916030288400269104140792886215078424516709087000699282120660418371806535567252532567532861291042487761825829765157959847035622262934860034158722980534989650226291748788202734209222245339856264766914905562842503912757710284027998066365825488926488025456610172967026640765590429099456815065265305371829412703369313785178609040708667114965583434347693385781711386455873678123014587687126603489139095620099393610310291616152881384379099042317473363948045759314931405297634757481193567091101377517210080315590248530906692037671922033229094334676851422144773793937517034436619910403375111735471918550464490263655128162288244625759163330391072253837421821408835086573917715096828874782656995995744906617583441375223970968340800535598491754173818839994469748676265516582765848358845314277568790029095170283529716344562129640435231176006651012412006597558512761785838292041974844236080071930457618932349229279650198751872127267507981255470958904556357921221033346697499235!63025494780249011419521238281530911407907386025152274299581807247162591668545133312394804947079119153267343028244186041426363954800044800267049624820179289647669758318327131425170296923488962766844032326092752496035799646925650493681836090032380929345958897069536534940603402166544375589004563288225054525564056448246515187547119621844396582533754388569094113031509526179378002974120766514793942590298969594699556576121865619673378623625612521632086286922210327488918654364802296780705765
Слайд 19
Вывод
Число Пи является удивительным и загадочным числом. Возможно в нем закодировано
Мы провели исследование по закономерности числа Пи.
Мы, Даша и Лиза искали закономерность более 3-х месяцев, но так ни чего и не нашли. Мы привлекли к поиску закономерности своих родителей, друзей и учителей, но попытки оказались напрасными.
Нам кажется что закономерность, где-то есть, но мы ее просто не видим.