- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Модуль 1. презентация
Содержание
- 1. Модуль 1.
- 2. Лекция 5 Базисные средства манипулирования
- 3. 1. Базовые операции Алгебры A Базис Алгебры
- 4. Реляционные аналоги логических операций позволяют выражать напрямую:
- 5. Путем комбинирования базовых операций выражаются операции :
- 6. Условные обозначения r – отношение A
- 7. 1. Базовые операции Алгебры A Условные обозначения
- 8. Условные обозначения еxists - квантор существования
- 9. 1. Базовые операции Алгебры A Условные обозначения
- 10. 1. Базовые операции Алгебры A Операция реляционного
- 11. 1. Базовые операции Алгебры A Операция реляционного
- 12. 1. Базовые операции Алгебры A Операция реляционного
- 13. Базовые операции Алгебры A Операция удаления атрибута
- 14. Базовые операции Алгебры A Операция удаления атрибута
- 15. Базовые операции Алгебры A Операция удаления атрибута
- 16. Базовые операции Алгебры A Операция переименования Пусть
- 17. Базовые операции Алгебры A Операция переименования Тогда:
- 18. Базовые операции Алгебры A Операция реляционной конъюнкции
- 19. Базовые операции Алгебры A Операция реляционной конъюнкции
- 20. Базовые операции Алгебры A Операция реляционной конъюнкции
- 21. Базовые операции Алгебры A Операция реляционной дизъюнкции
- 22. Базовые операции Алгебры A Операция реляционной дизъюнкции
- 23. Базовые операции Алгебры A Операция реляционной дизъюнкции
- 24. 2. Полнота и избыточность Алгебры A
- 26. Результат операции MINUS 2. Полнота и избыточность Алгебры A Выводимость операции взятия разности
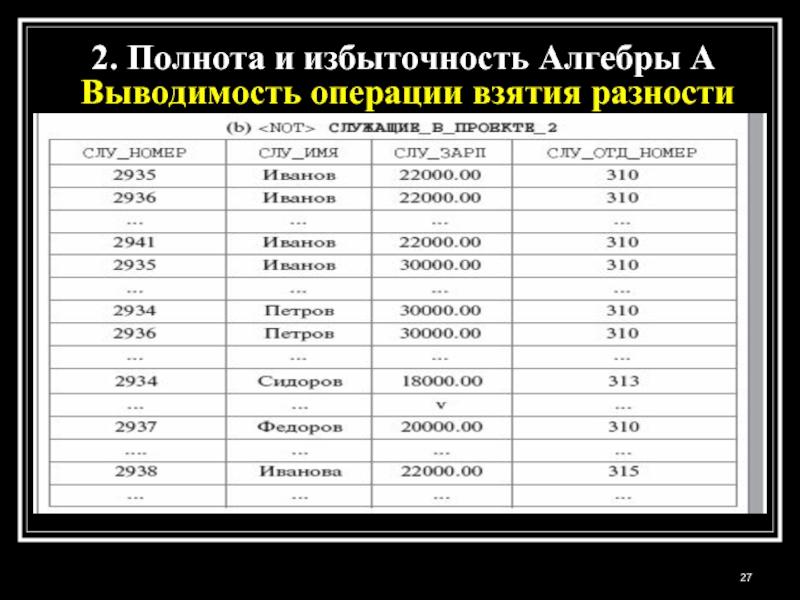
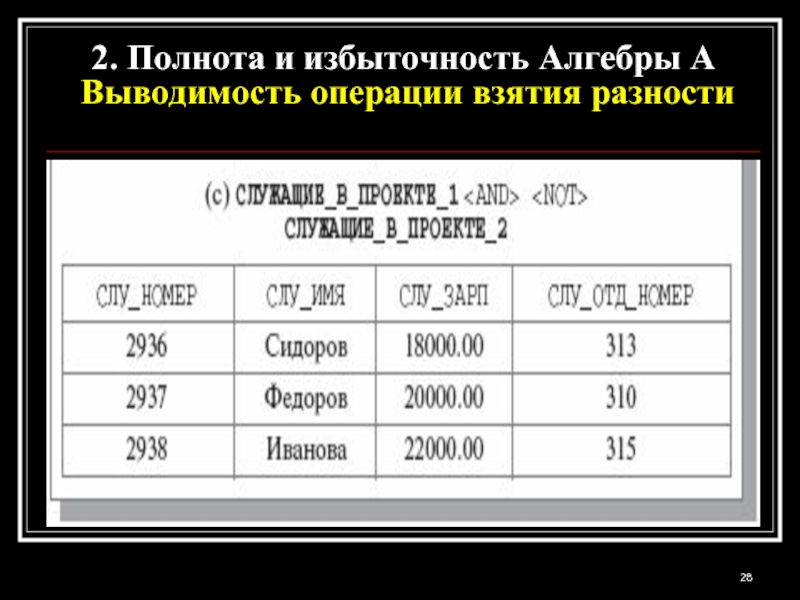
- 27. 2. Полнота и избыточность Алгебры A Выводимость операции взятия разности
- 28. 2. Полнота и избыточность Алгебры A Выводимость операции взятия разности
- 29. 2. Полнота и избыточность Алгебры A
- 30. 2. Полнота и избыточность Алгебры A
Слайд 2Лекция 5 Базисные средства манипулирования реляционными данными: алгебра A Дейта и
Дарвена
1. Базовые операции Алгебры A
2. Полнота и избыточность Алгебры A
Слайд 31. Базовые операции Алгебры A
Базис Алгебры A
реляционное отрицание (дополнение)
реляционная конъюнкция
(или дизъюнкция)
проекция (удаления атрибута)
проекция (удаления атрибута)
Слайд 4Реляционные аналоги логических операций позволяют выражать напрямую:
операции пересечения
декартова произведения
естественного соединения
объединения отношений и т. д.
естественного соединения
объединения отношений и т. д.
1. Базовые операции Алгебры A
Слайд 5Путем комбинирования базовых операций выражаются операции :
переименования атрибутов
соединения
общего вида
взятия разности отношений
взятия разности отношений
1. Базовые операции Алгебры A
Слайд 6Условные обозначения
r – отношение
A – имя атрибута отношения r
T
– имя соответствующего типа (типа или домена)
v – значение типа T.
заголовок Hr отношения r - множество атрибутов (упорядоченных пар вида)
v – значение типа T.
заголовок Hr отношения r - множество атрибутов (упорядоченных пар вида
1. Базовые операции Алгебры A
Слайд 71. Базовые операции Алгебры A
Условные обозначения
никакие два атрибута в этом множестве
не могут содержать одинаковое имя атрибута A;
кортеж tr, соответствующий заголовку Hr, – множество упорядоченных триплетов вида
тело Br отношения r – это множество кортежей tr.
кортеж tr, соответствующий заголовку Hr, – множество упорядоченных триплетов вида
тело Br отношения r – это множество кортежей tr.
Слайд 8Условные обозначения
еxists - квантор существования
exists tr означает «существует такой tr,
что»
Символ «∈» означает принадлежность одного множества другому;
tr ∈ Br означает, что элемент tr принадлежит множеству Br.
tr ∉ Br означает, что элемент tr не принадлежит множеству Br
Символ «∈» означает принадлежность одного множества другому;
tr ∈ Br означает, что элемент tr принадлежит множеству Br.
tr ∉ Br означает, что элемент tr не принадлежит множеству Br
1. Базовые операции Алгебры A
Слайд 91. Базовые операции Алгебры A
Условные обозначения
имена реляционных операций берутся в угловые
скобки: , , и т. д.
Слайд 101. Базовые операции Алгебры A
Операция реляционного дополнения
Пусть s обозначает результат операции
Hs = Hr (заголовок результата совпадает с заголовком операнда);
Bs = {ts : exists tr (tr ∉ Br and ts = tr) }
(в тело результата входят все кортежи, соответствующие заголовку и не входящие в тело операнда).
Слайд 111. Базовые операции Алгебры A
Операция реляционного дополнения
Операция производит дополнение s
заданного отношения r
Заголовком s является заголовок r
Тело s включает все кортежи, соответствующие этому заголовку и не входящие в тело r.
Заголовком s является заголовок r
Тело s включает все кортежи, соответствующие этому заголовку и не входящие в тело r.
Слайд 121. Базовые операции Алгебры A
Операция реляционного дополнения
Пусть в состав домена ДОПУСТИМЫЕ_НОМЕРА_ПРОЕКТОВ
входит
всего пять значений {1, 2, 3, 4, 5}
Слайд 13Базовые операции Алгебры A
Операция удаления атрибута
Пусть s - результат операции r
Для обеспечения возможности выполнения операции требуется, чтобы существовал некоторый тип (или домен) T такой, что
(т. е. в состав заголовка отношения r должен входить атрибут A).
Слайд 14Базовые операции Алгебры A
Операция удаления атрибута
Тогда:
Hs = Hr minus {
T>}
заголовок результата получается из заголовка операнда изъятием атрибута A;
Bs = {ts : exists tr exists v (tr∈ Br and v ∈T and∈ tr and ts = tr minus {})} в тело результата входят все кортежи операнда, из которых удалено значение атрибута A.
заголовок результата получается из заголовка операнда изъятием атрибута A;
Bs = {ts : exists tr exists v (tr∈ Br and v ∈T and
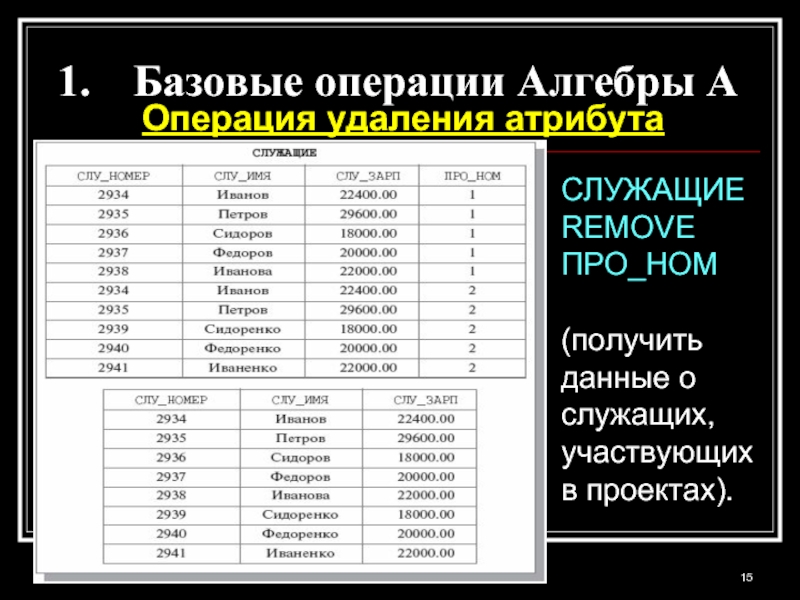
Слайд 15Базовые операции Алгебры A
Операция удаления атрибута
СЛУЖАЩИЕ REMOVE
ПРО_НОМ
(получить
данные о
служащих, участвующих
в проектах).
Слайд 16Базовые операции Алгебры A
Операция переименования
Пусть s - результат операции r
(A, B)
Для выполнения операции требуется, чтобы существовал некоторый тип T, такой, что
∈ Hr, и чтобы не существовал такой тип
T, что ∉ Hr
(в схеме отношения r должен присутствовать атрибут A и не должен присутствовать атрибут B.)
Для выполнения операции требуется, чтобы существовал некоторый тип T, такой, что
T, что
(в схеме отношения r должен присутствовать атрибут A и не должен присутствовать атрибут B.)
Слайд 17Базовые операции Алгебры A
Операция переименования
Тогда:
Hs = (Hr minus {}) union
{}
в схеме результата B заменяет A
Bs = {ts : exists tr exists v (tr∈ Br and v ∈T and ∈tr and ts = (tr minus {}) union {})}
в кортежах тела результата имя значений атрибута A меняется на B.
в схеме результата B заменяет A
Bs = {ts : exists tr exists v (tr∈ Br and v ∈T and
в кортежах тела результата имя значений атрибута A меняется на B.
Слайд 18Базовые операции Алгебры A
Операция реляционной конъюнкции
Пусть s - результат операции r1
Для выполнения операции требуется, чтобы если
то T1=T2
(если в двух отношениях-операндах имеются одноименные атрибуты, то они должны быть определены на одном и том же типе (домене).)
Слайд 19Базовые операции Алгебры A
Операция реляционной конъюнкции
Тогда:
Hs = Hr1 union Hr2
заголовок
результата получается путем объединения заголовков отношений
Bs = { ts : exists tr1 exists tr2 ((tr1∈ Br1 and tr2∈ Br2) and ts = tr1 union tr2)}
кортеж результата определяется как объединение кортежей операндов
Bs = { ts : exists tr1 exists tr2 ((tr1∈ Br1 and tr2∈ Br2) and ts = tr1 union tr2)}
кортеж результата определяется как объединение кортежей операндов
Слайд 20Базовые операции Алгебры A
Операция реляционной конъюнкции
если схемы отношений-операндов имеют непустое
пересечение, то операция работает как естественное соединение
если пересечение схем операндов пусто, то работает как расширенное декартово произведение
если схемы отношений полностью совпадают, то результатом операции является пересечение двух отношений
если пересечение схем операндов пусто, то
если схемы отношений полностью совпадают, то результатом операции является пересечение двух отношений
Слайд 21Базовые операции Алгебры A
Операция реляционной дизъюнкции
Пусть s обозначает результат операции
r1
Для обеспечения операции требуется, чтобы
если
то T1 = T2
одноименные атрибуты должны быть определены на одном и том же типе
Слайд 22Базовые операции Алгебры A
Операция реляционной дизъюнкции
Тогда:
Hs = Hr1 union Hr2
из схемы результата удаляются атрибуты-дубликаты
Bs = { ts : exists tr1 exists tr2 ((tr1∈ Br1 or tr2 ∈Br2) and ts = tr1 union tr2)}
Слайд 23Базовые операции Алгебры A
Операция реляционной дизъюнкции
при этом:
если у операндов нет
общих атрибутов, то в тело результата входят все ts, которые являются объединением tr1 и tr2, и хотя бы один из этих кортежей принадлежит телу одного из операндов;
если у операндов есть общие атрибуты, то в тело результата входят все ts, которые являются объединением кортежей tr1 и tr2, если хотя бы один из этих кортежей принадлежит телу одного из операндов, и значения общих атрибутов tr1 и tr2 совпадают;
если же схемы операндов совпадают, то тело результата является объединением тел операндов.
если у операндов есть общие атрибуты, то в тело результата входят все ts, которые являются объединением кортежей tr1 и tr2, если хотя бы один из этих кортежей принадлежит телу одного из операндов, и значения общих атрибутов tr1 и tr2 совпадают;
если же схемы операндов совпадают, то тело результата является объединением тел операндов.
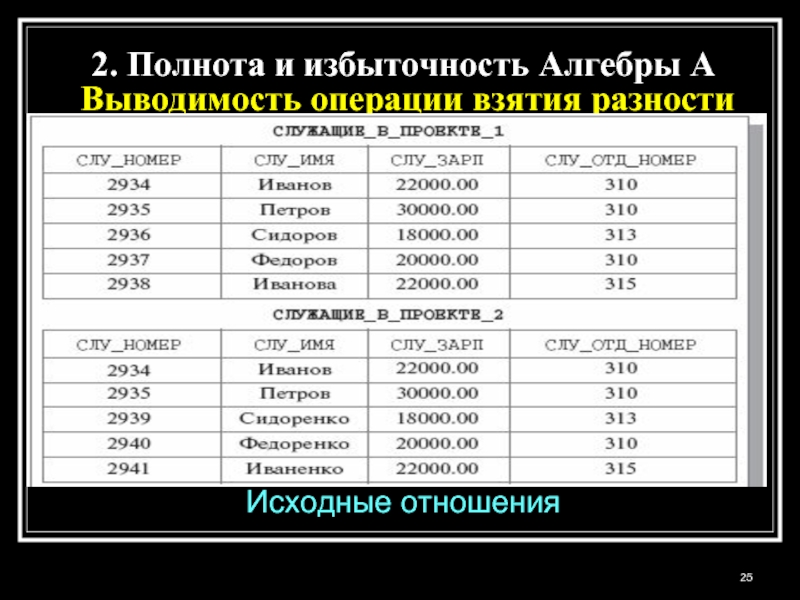
Слайд 242. Полнота и избыточность Алгебры A
в состав базовых операций Алгебры
A входят
операция в качестве аналога операции PROJECT, и операция переименования атрибутов .
UNION является частным случаем операции,
TIMES, INTERSECT и NATURAL JOIN –
частные случаи операции.
Покажем, что через операции Алгебры A
выражаются операции взятия разности MINUS,
ограничения (WHERE), соединения общего вида (JOIN)
и реляционного деления (DIVIDE BY).
операция
UNION является частным случаем операции
TIMES, INTERSECT и NATURAL JOIN –
частные случаи операции
Покажем, что через операции Алгебры A
выражаются операции взятия разности MINUS,
ограничения (WHERE), соединения общего вида (JOIN)
и реляционного деления (DIVIDE BY).
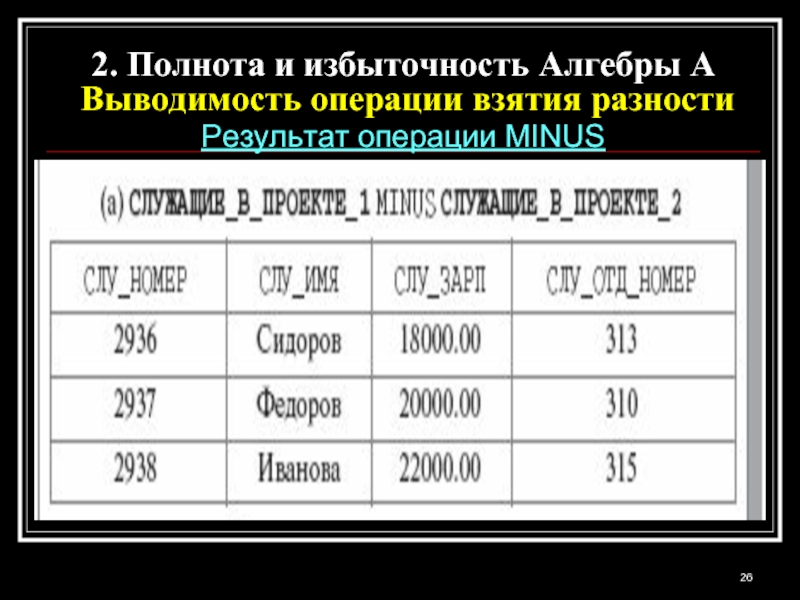
Слайд 26Результат операции MINUS
2. Полнота и избыточность Алгебры A
Выводимость операции взятия
разности
Слайд 292. Полнота и избыточность Алгебры A
Интерпретация операции ограничения
операция ограничения
r
WHERE comp
где r – отношение,
comp – простое условие ограничения
где r – отношение,
comp – простое условие ограничения
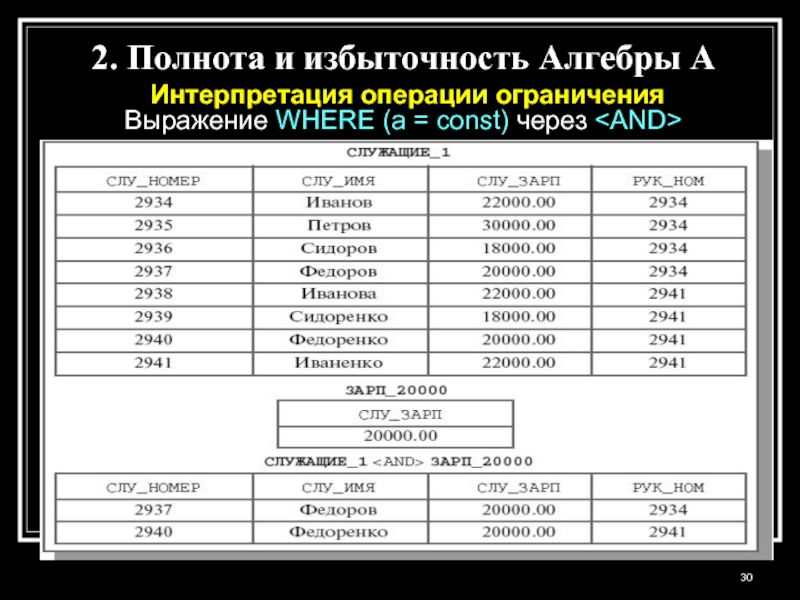
Слайд 302. Полнота и избыточность Алгебры A
Интерпретация операции ограничения
Выражение WHERE (a
= const) через