- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Модели многогранников презентация
Содержание
- 1. Модели многогранников
- 2. Использование презентации На слайдах презентации Вы можете
- 3. Кубооктаэдр. Кубооктаэдр – полуправильный многогранник. Он строится
- 4. Звёздчатый октаэдр (stella octangula Кеплера) Является объединением
- 5. Большой додекаэдр Для этой модели нужен трафарет
- 6. Соединение десяти тетраэдров Девятая звёздчатая форма икосододекаэдра.
- 7. Девятая звёздчатая форма икосаэдра В показанной на
- 8. Большой икосаэдр Икосаэдр имеет двадцать граней. Если
- 9. Большой бритогональный додекоикосододекаэдр Показанный на фотографии многогранник
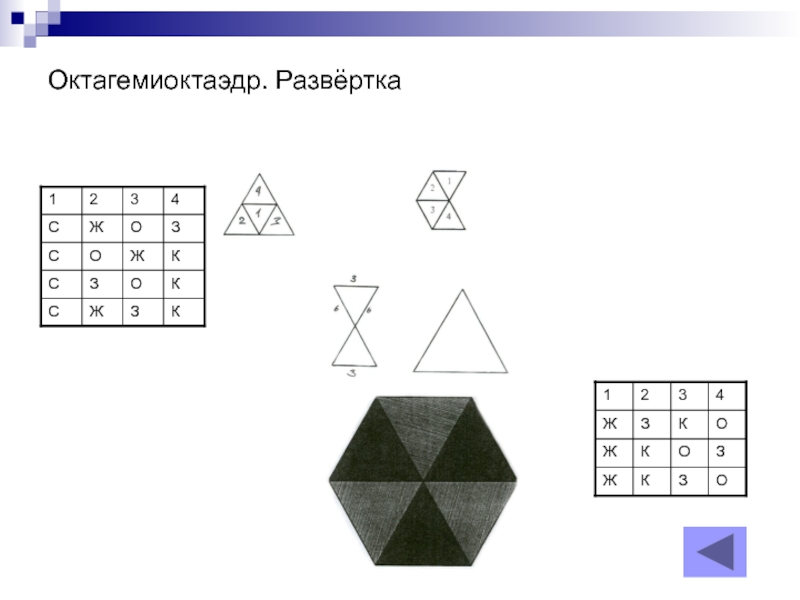
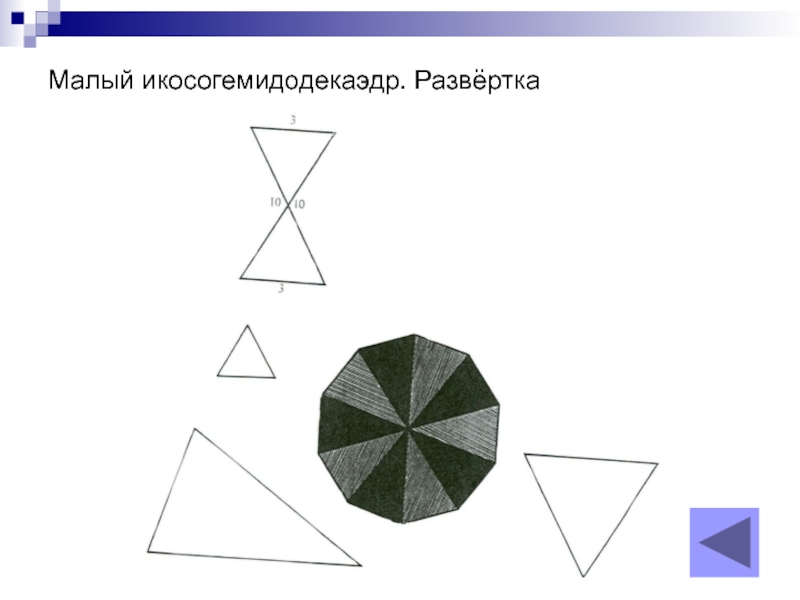
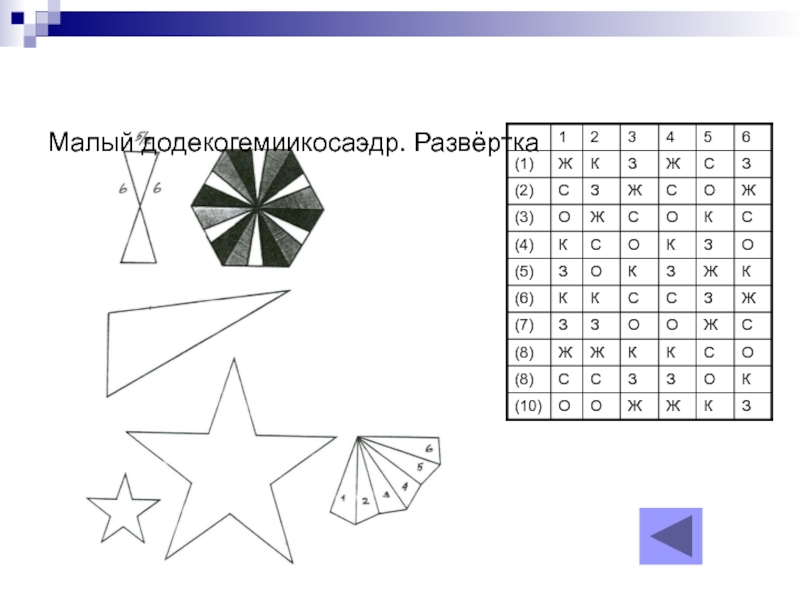
- 10. А также развёртки моделей Октагемиоктаэдр Малый икосогемиоктаэдр Малый додекогемиикосаэдр
- 11. Кубооктаэдр. Развёртка.
- 12. Звёздчатый октаэдр. Развёртка
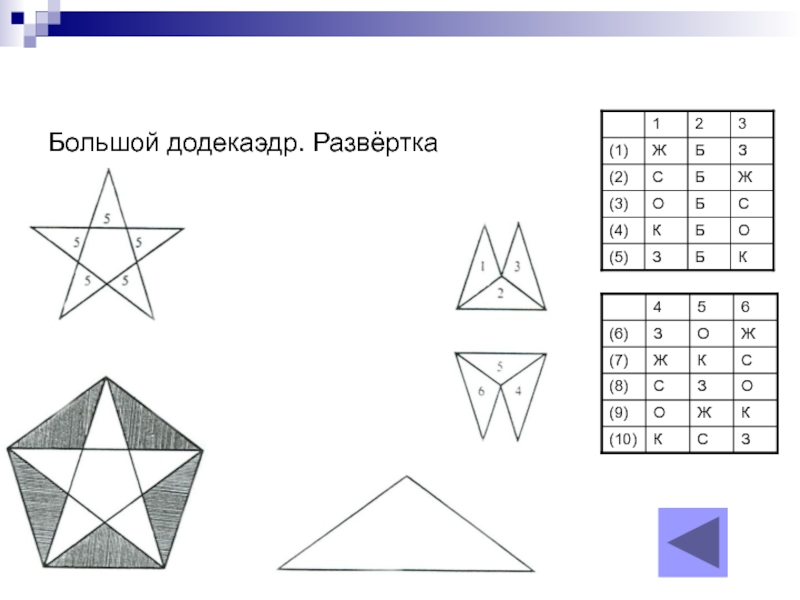
- 13. Большой додекаэдр. Развёртка
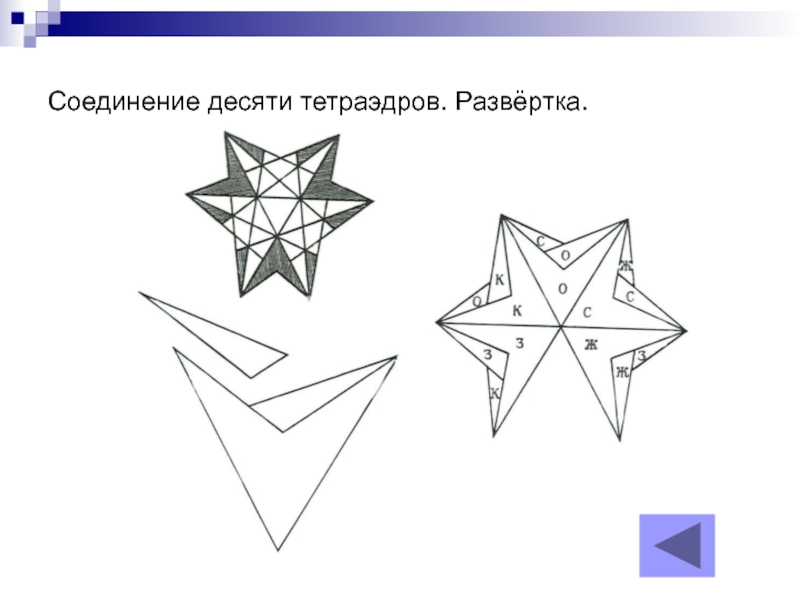
- 14. Соединение десяти тетраэдров. Развёртка.
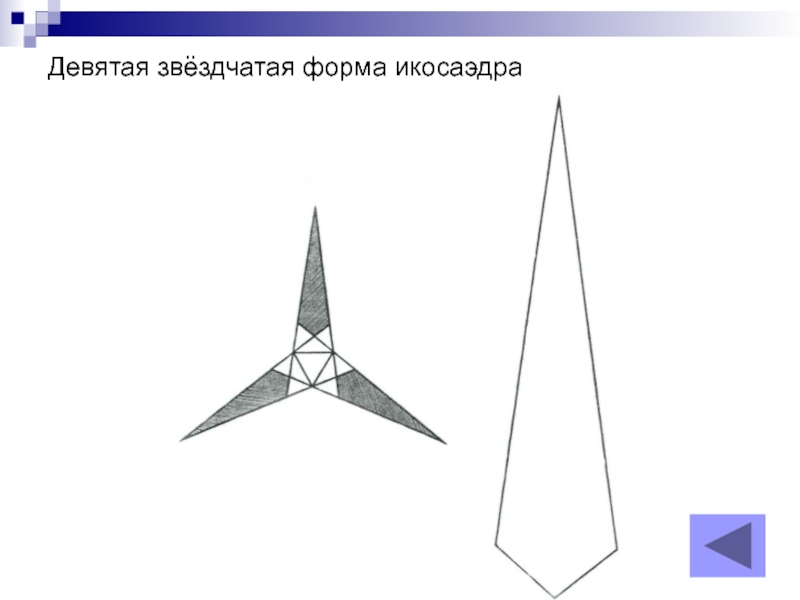
- 15. Девятая звёздчатая форма икосаэдра
- 16. Большой икосаэдр. Развёртка
- 17. Октагемиоктаэдр. Развёртка
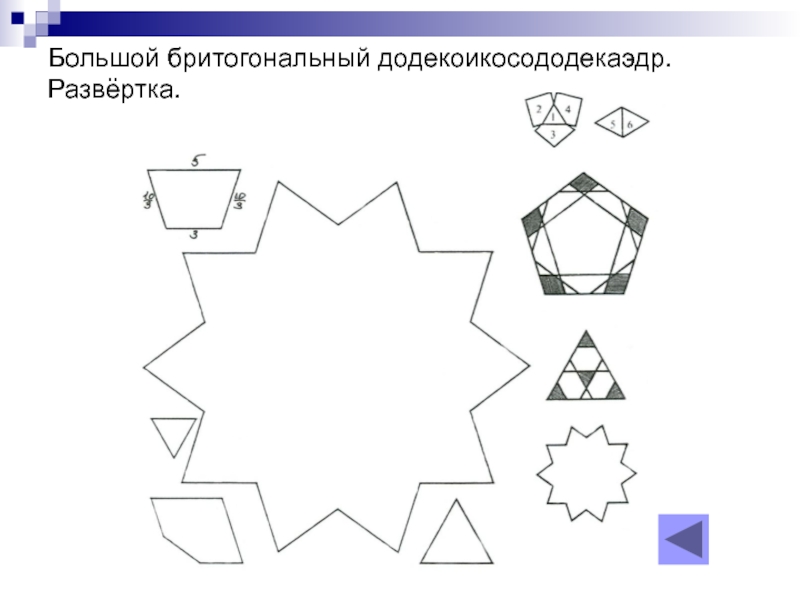
- 18. Большой бритогональный додекоикосододекаэдр. Развёртка.
- 19. Малый икосогемидодекаэдр. Развёртка
- 20. Малый додекогемиикосаэдр. Развёртка
Слайд 2Использование презентации
На слайдах презентации Вы можете найти информацию о методе конструирования
Некоторые слайды не содержат подробного описания модели, так как она уже описана на странице Stars (student_support). Более полную информацию модно найти в книге М. Веннинждера «Модели многогранников», а также на сайте
http://wenninger.narod.ru
Слайд 3Кубооктаэдр.
Кубооктаэдр – полуправильный многогранник. Он строится так: в кубе проводятся отсекающие
При создании модели, прежде всего подклейте к одному треуцгольнику три квадрата, затем с помощью трёх треугольников склете наподобие чаши с треугольным дном и стенками, составленными из квадратов и треугольников, которые чееррдуются между собой. По окончании этой работы Вы получите половину модели. После этого вам будет не трудно подклеить недостающие грани. Проследите только за тем, чтобы противоположные грани имели один и тот же цвет.
Важнейшим свойством этого многогранника является то, что он имеет грани двух типов. Причём каждая грань одного типа соседствует только с гранями другого типа. Такие многогранники называются квазиправильными.
Посмотреть развёртку.
Слайд 4Звёздчатый октаэдр (stella octangula Кеплера)
Является объединением двух пересекающихся правильных тетраэдров, и
Посмотреть развёртку
Слайд 5Большой додекаэдр
Для этой модели нужен трафарет - равнобедренный треугольник с углами
Посмотреть развёртку
Слайд 6Соединение десяти тетраэдров
Девятая звёздчатая форма икосододекаэдра.
Многогранник представляет собой соединение 10 тетраэдров,
Посмотреть развёртку
Слайд 7Девятая звёздчатая форма икосаэдра
В показанной на рисунке заготовке вы легко узнаете
Сначала следует придать пикам обычную пятигранную форму, соблюдая при этом привычные правила икосаэдральной раскраски. Затем все части соединяют между собой посредством наклеек на основаниях пиков. Можно разместить пики так, что каждая грань звёздчатого многогранника окажется одноцветной. Однако порядок такого размещения не очевиден, и вам придётся немного поломать голову, чтобы его найти. В этой модели, как и в предыдущей, трудно подклеить на место последний пик из-за отсутствия доступа к наклейкам внутри модели.
Посмотреть развёртку
Слайд 8Большой икосаэдр
Икосаэдр имеет двадцать граней. Если каждую из них продолжить неограниченно,
Посмотреть развёртку
Слайд 9Большой бритогональный додекоикосододекаэдр
Показанный на фотографии многогранник относится к семейству икосододекаэдров. Это
Простейший метод построения этой модели сводится к попеременной подклейке между лучами декаграмм заранее приготовленных выемок и желобков. Начните с белой (Б) десятиугольной звезды, подклеивая к ней показанные ниже части, и закончите работу обычным способом.
Посмотреть развёртку