- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Множества+отношения презентация
Содержание
- 1. Множества+отношения
- 2. Множество - это соединение, совокупность, собрание некоторых
- 3. Множество, которое не содержит ни одного элемента,
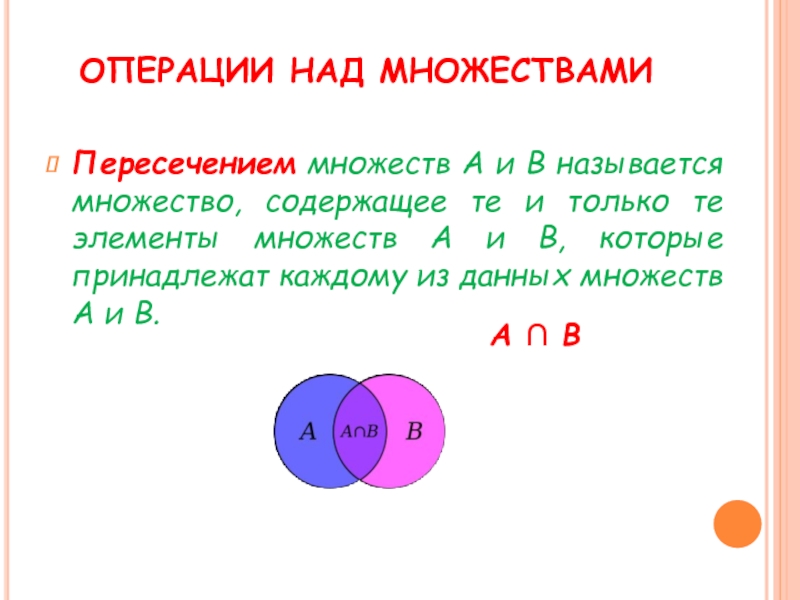
- 4. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ Пересечением множеств А и
- 5. Пересечение множеств Свойства: коммуникативность А ∩В=В ∩А;
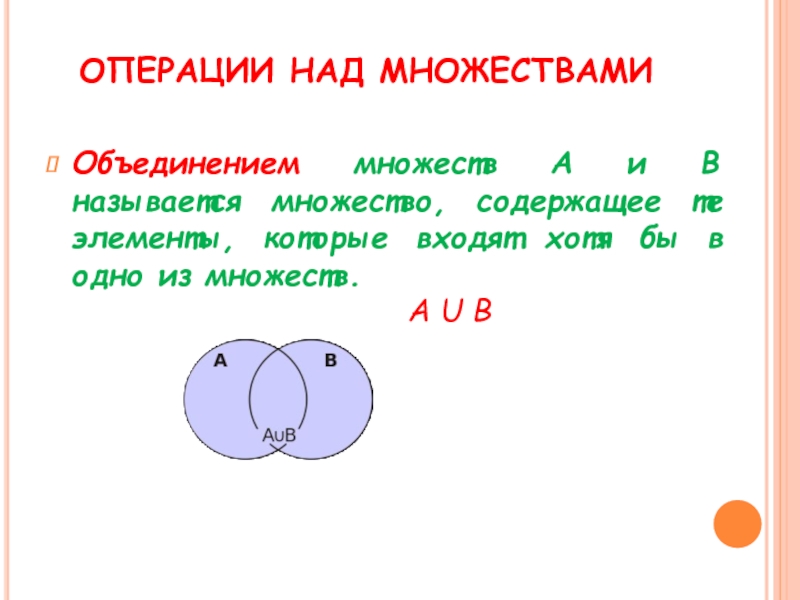
- 6. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ Объединением множеств А и
- 7. Объединение множеств . Свойства: АUВ=ВUА; АU(ВUС)=(АUВ)UС;
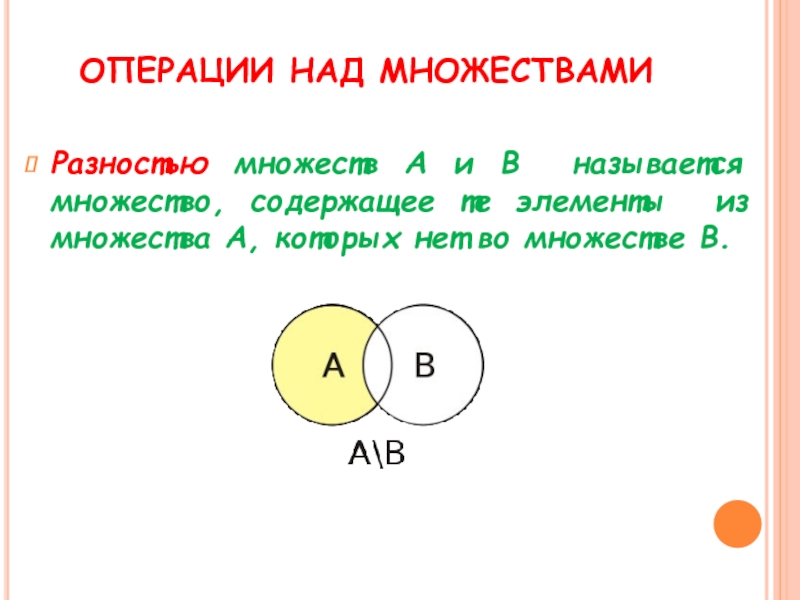
- 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ Разностью множеств А и
- 9. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ Декартовым произведением множеств А
- 10. ОТНОШЕНИЯ Отношение – это некоторое подмножество пар
- 11. СВОЙСТВА ОТНОШЕНИЙ рефлексивность: если а ϵ
- 12. ВИДЫ ОТНОШЕНИЙ Отношения между элементами множества: Отношения между числами (=; >; следует из другого.
Слайд 2Множество - это соединение, совокупность, собрание некоторых предметов, объединённых по какому-либо
Например:
множество студентов группы;
множество целых чисел;
множество точек на прямой;
множество книг на полке
Слайд 3Множество, которое не содержит ни одного элемента, называют пустым и обозначают
Обозначения: А,В,С,Д - множества,
αЄА (элемент α принадлежит множеству А);
{1,2,3} (элемент 4 не принадлежит множеству).
4
Слайд 4ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
Пересечением множеств А и В называется множество, содержащее те
А ∩ В
Слайд 5Пересечение множеств
Свойства:
коммуникативность А ∩В=В ∩А;
ассоциативность (А∩В) ∩С=А∩(В ∩С);
если В ⊂А, то А ∩В=В
А ∩ Ø =Ø
.
Слайд 6ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
Объединением множеств А и В называется множество, содержащее те
А U В
Слайд 8ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
Разностью множеств А и В называется множество, содержащее те
Слайд 9ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
Декартовым произведением множеств А и В называется множество пар
АхВ={(а;b)| а Є А,b Є В}
Слайд 10ОТНОШЕНИЯ
Отношение – это некоторое подмножество пар декартова произведения множеств А и
Обозначается:
a R b (элемент а находится в отношении с элементом b).
Слайд 11СВОЙСТВА ОТНОШЕНИЙ
рефлексивность:
если а ϵ А , то а R a;
симметричность:
если а, b ϵ А и а R b, то b R a;
транзитивность:
если а, b, с ϵ А, а R b и с R b, то а R с.
Если отношение R обладает свойствами 1-3,
то оно называется отношением эквивалентности.
Слайд 12ВИДЫ ОТНОШЕНИЙ
Отношения между элементами множества:
Отношения между числами (=; >;
Отношения между точками на прямой
(предшествует, следует за…);
Отношения между прямыми
(параллельности, перпендикулярности);
Отношения между геометрическими фигурами
(равенство, подобие, конгруэнтность);
Отношения между множествами
(объединение, пересечение, разность);
Отношения между высказываниями:
<=> эквивалентно (равносильно);
=> следует из другого.