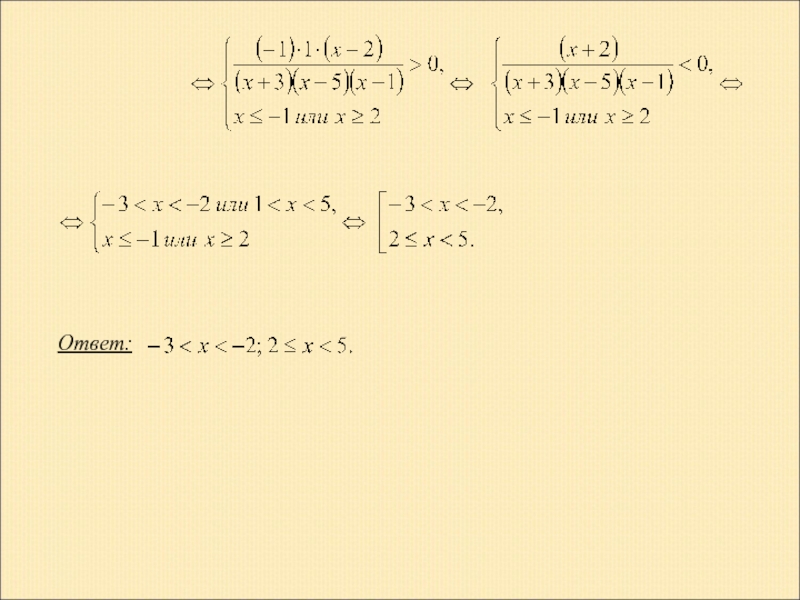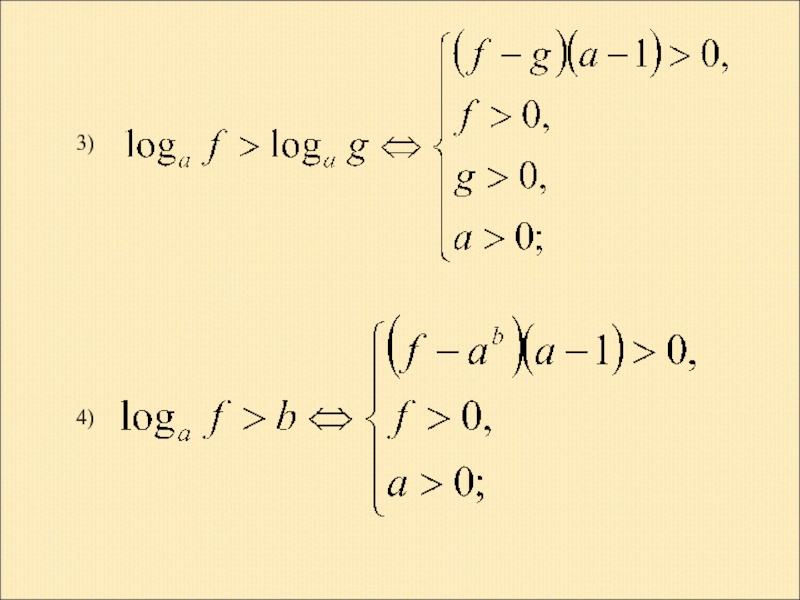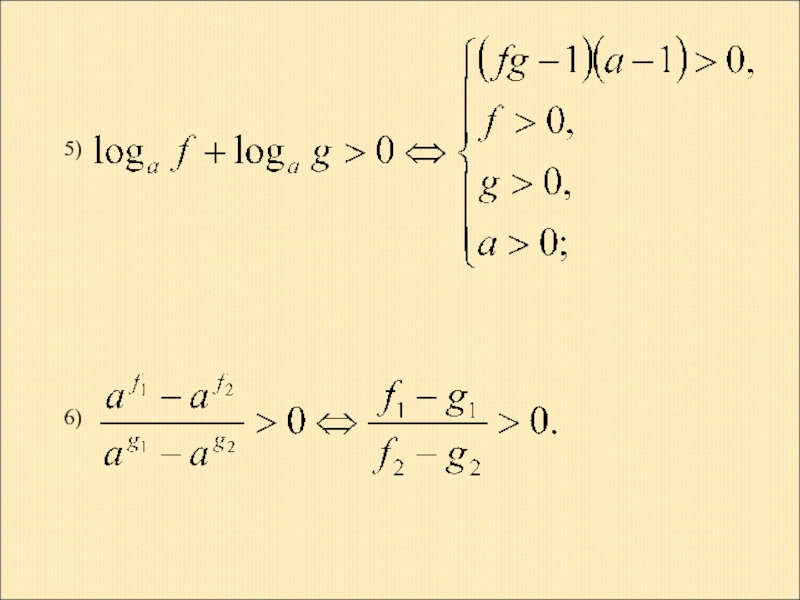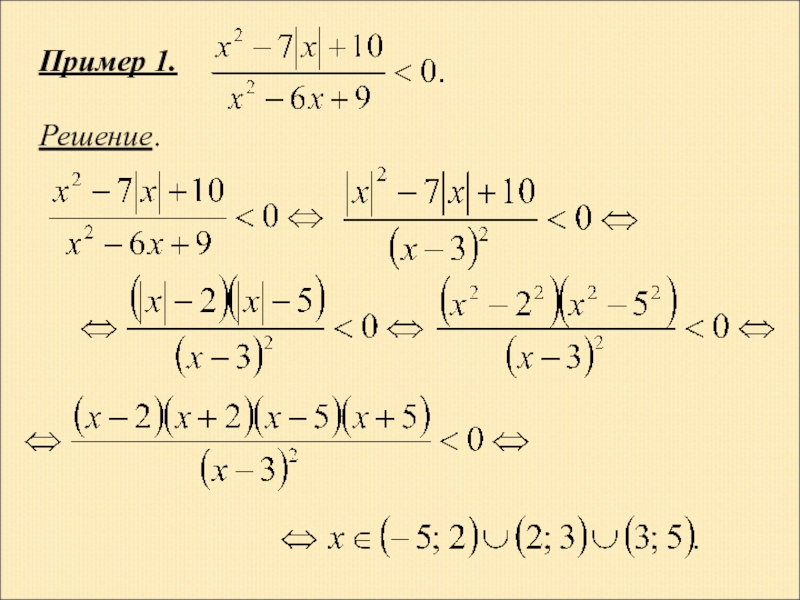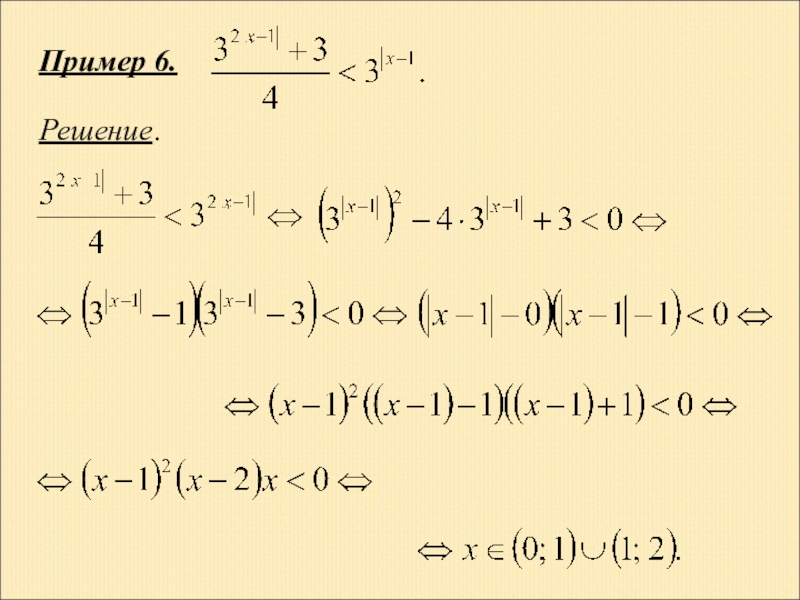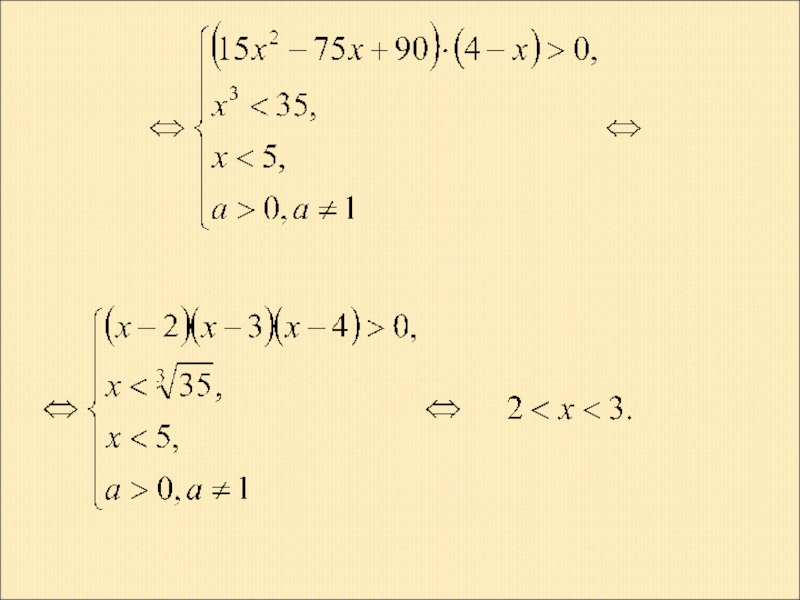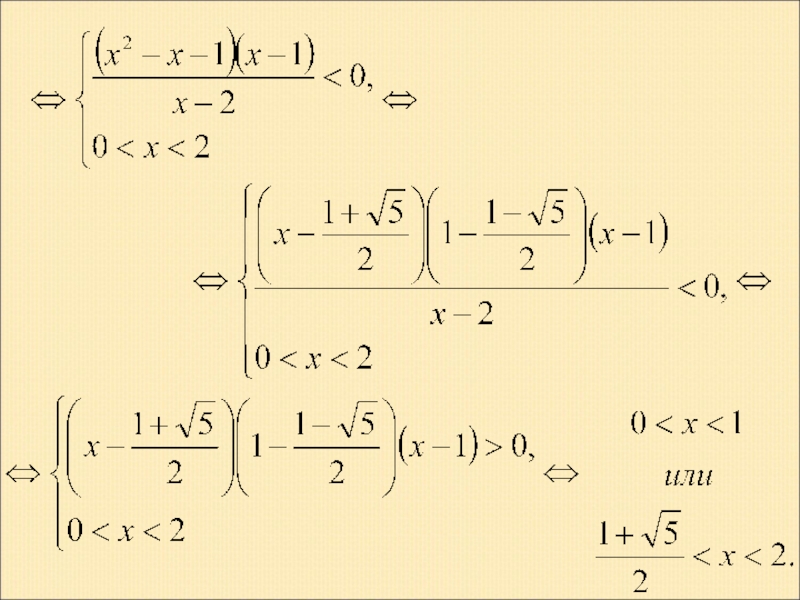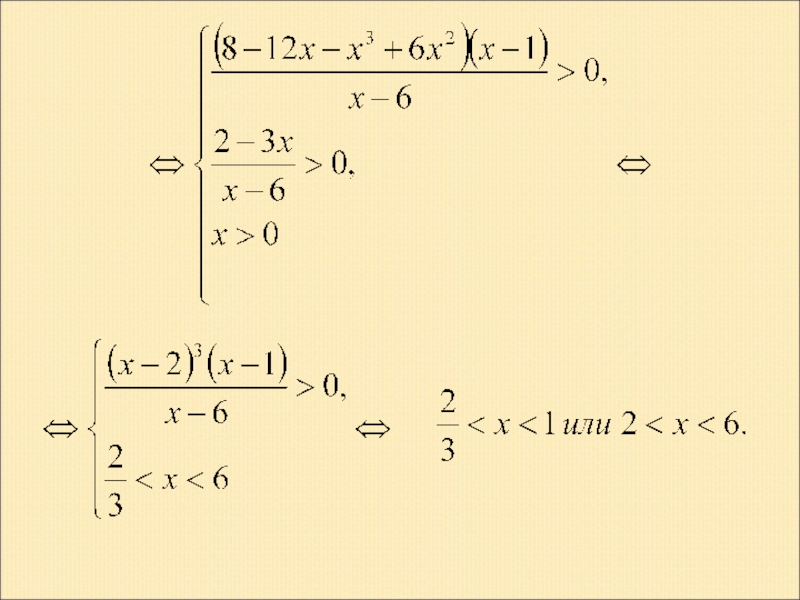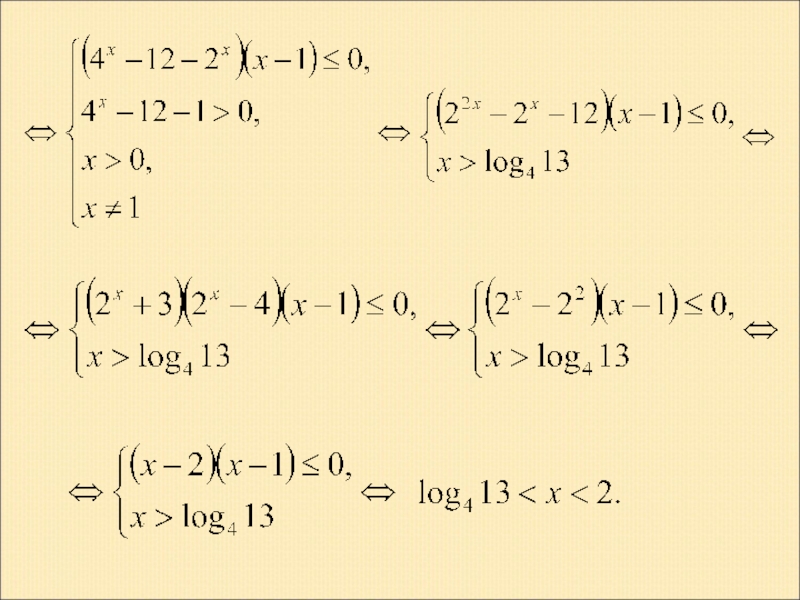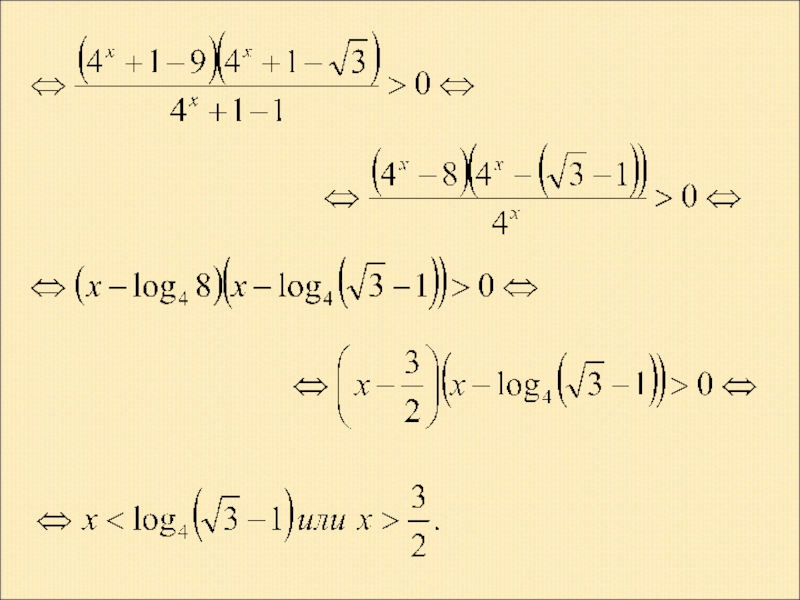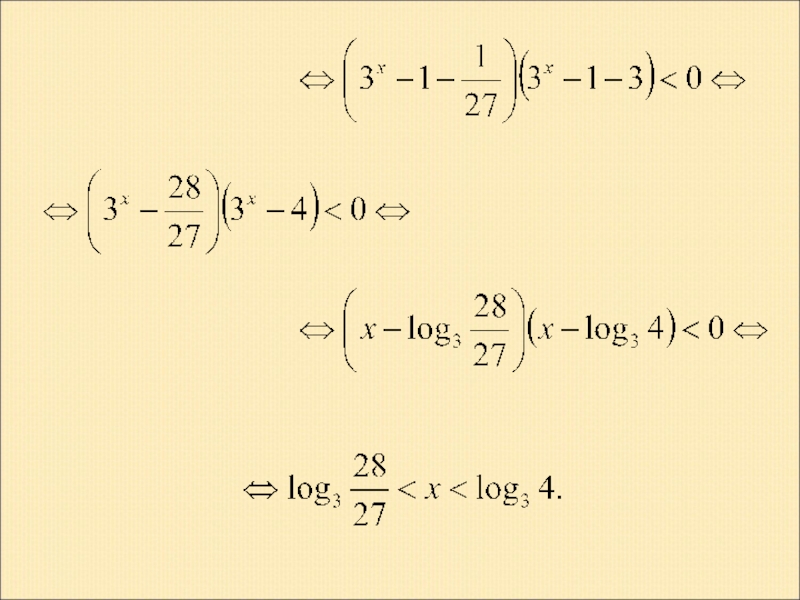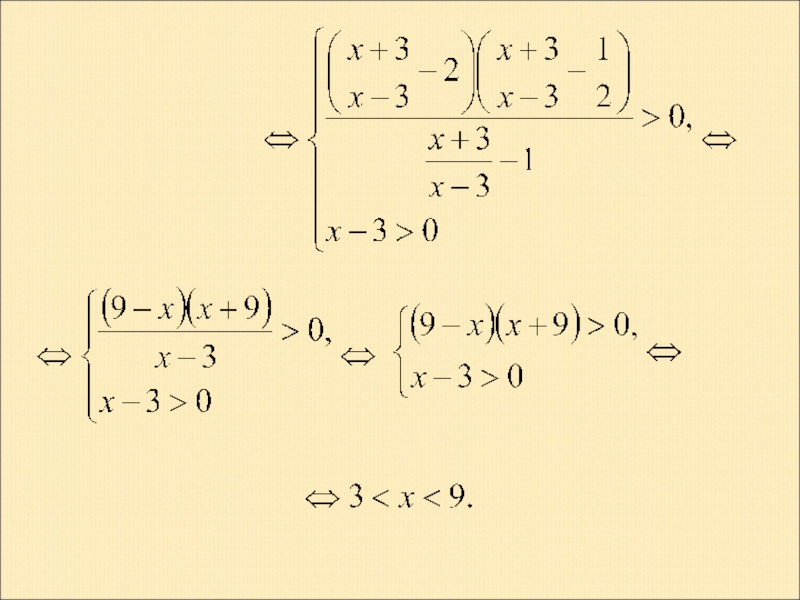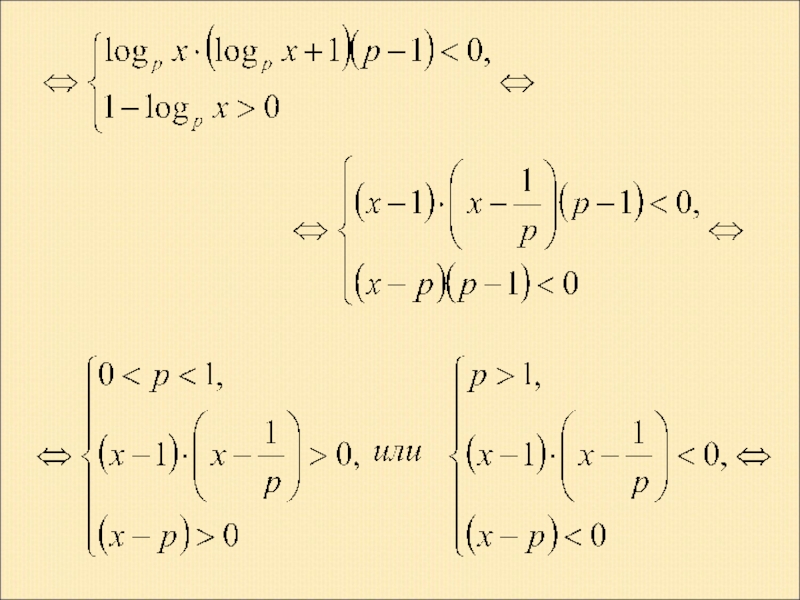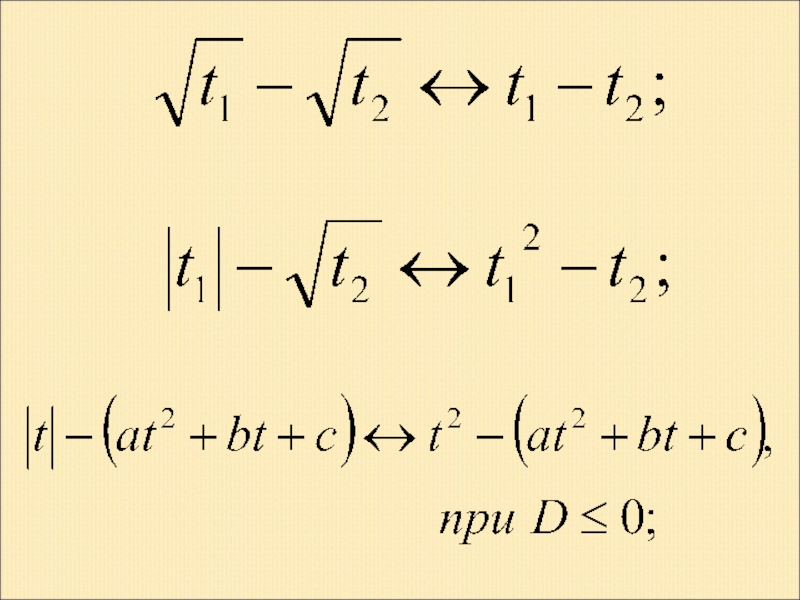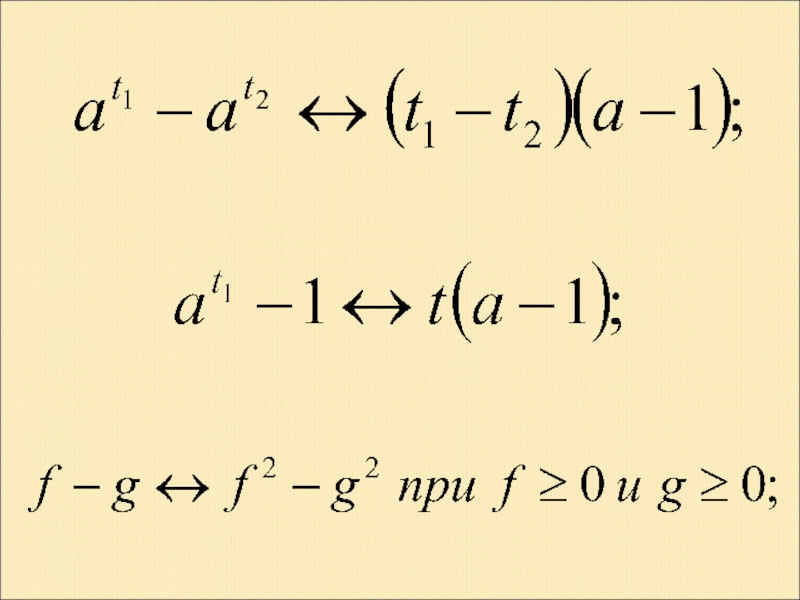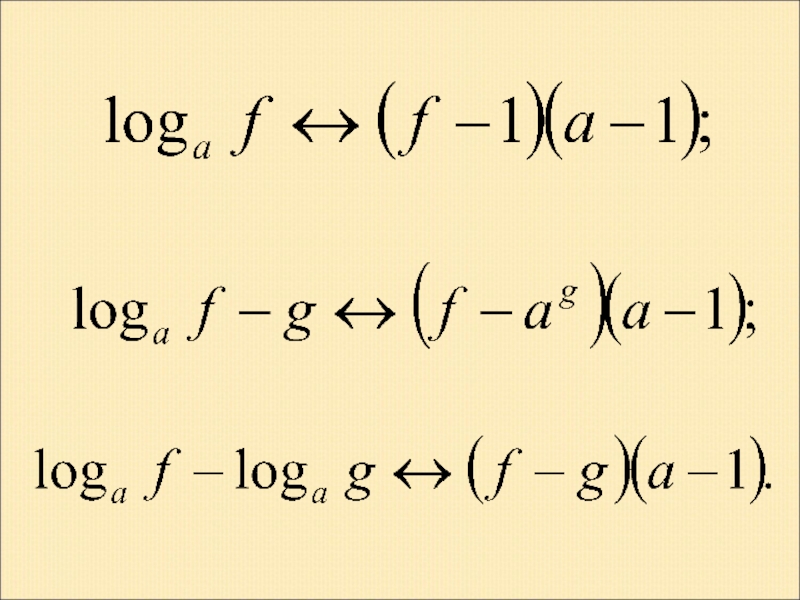Руководитель: учитель математики Ускова Н.Н.
МОУ лицей №60
2011 г.
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод Замены множителейКуфтерин павел, радченко сергей, шахтарин никита 11 классМоу Лицей № 60 презентация
Содержание
- 1. Метод Замены множителейКуфтерин павел, радченко сергей, шахтарин никита 11 классМоу Лицей № 60
- 2. Теоретическая часть
- 3. Основная идея метода Любое неравенство приводимо к
- 4. Монотонность – ключ к замене Утверждение 1.
- 5. Функция
- 6. Пример 1. Решить неравенство Решение (подробное). Исходное
- 7. где знакопостоянные (D
- 8. Ответ:
- 9. Две любопытные замены: (9) (10) Замена (9)
- 10. Пример 2. Решить неравенство Решение. Ответ:
- 11. Пример 3. Решить неравенство Решение. В этом
- 12. так как при x>0 (x+1) и (3x+14) – положительные числа Ответ.
- 13. Показательная и логарифмическая функция и вызываемые
- 14. Функция
- 15. Для логарифмической функции
- 16. Замечание. Утверждения (14) и (13) равносильны, поскольку
- 17. 3) 4)
- 18. 6) 5)
- 19. Практическая часть Решение неравенств
- 20. Пример 1. Решение.
- 21. Пример 2. Решение.
- 22. Пример 3. Решение.
- 23. Пример 4. Решение.
- 24. Пример 5. Решение.
- 25. Пример 6. Решение.
- 26. Пример 7. Решение.
- 27. Пример 8. Решение.
- 29. Пример 9. Решение.
- 31. Пример 10. Решение.
- 33. Пример 11. Решение.
- 35. Пример 12. Решение.
- 37. Пример 13. Решение.
- 39. Пример 14. Решение.
- 40. Пример 15. Решение.
- 42. Пример 16. Решение.
- 45. Пример 17. Решение.
- 47. Пример 18. Решение.
- 49. Пример 19. Решение.
- 50. Пример 20. Решение.
- 52. Итоги
- 53. I. Стандартный вид неравенств, когда применяется метод
- 54. II. Основная идея метода замены множителей состоит
- 55. III. Две основные замены: если f(t) –
- 56. IV. Наиболее часто встречающиеся замены (без учета ОДЗ):
- 60. ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА Голубев В. И. Метод замены
Слайд 1МЕТОД ЗАМЕНЫ МНОЖИТЕЛЕЙ КУФТЕРИН ПАВЕЛ, РАДЧЕНКО СЕРГЕЙ, ШАХТАРИН НИКИТА 11 КЛАСС МОУ ЛИЦЕЙ
Слайд 3Основная идея метода
Любое неравенство приводимо к виду
где символ «∨» обозначает один
(1)
Слайд 4Монотонность – ключ к замене
Утверждение 1. Функция
Утверждение 2. Функция есть строго убывающая тогда и только тогда, когда для любых двух значений из области определения функции разность совпадает по знаку с разностью , то есть
Комментарий. Практически, только замена знакопостоянных множителей не вытекает из этих утверждений. Поэтому, если нет желания трогать знак неравенства, всюду положительные множители просто убираем, а всюду отрицательные заменяем на (-1). Популярный знакопостоянный множитель – квадратный трехчлен с отрицательным дискриминантом – заменяем на старший коэффициент (или на свободный член), то есть
(2)
Слайд 5Функция и вызываемые ею замены
Поскольку
Функции и , рассматриваемые на множестве неотрицательных чисел, являются взаимнообратными и строго возрастающими, то есть
Поэтому
Так как и для любого m, то получаем, что
(3)
(4)
(7)
(6)
(5)
Слайд 6Пример 1. Решить неравенство
Решение (подробное). Исходное уравнение имеет вид
Все множители u1,
(8)
Так как и , то с учетом неотрицательности подкоренного выражения получаем:
Слайд 7где знакопостоянные (D
Слайд 9Две любопытные замены:
(9)
(10)
Замена (9) очень удобна там, где приходится отслеживать область
Замена (10) суммы при возможном одновременном равенстве нулю подкоренных выражений на сумму позволяет учитывать эту возможность.
Слайд 11Пример 3. Решить неравенство
Решение. В этом неравенстве уже нельзя множители
рассматривать как разности неотрицательных величин, так как выражения 3x и 2x в области допустимых значений (то есть при ) могут принимать как положительные, так и отрицательные значения. Однако, если область допустимых значений исходного неравенства разбить на два промежутка и (точка x=0 есть точка смены знака выражений 3x и 2x), то легко заметить, что на промежутке мы имеем произведение двух положительных чисел, и поэтому исходное неравенство ложно, а на втором промежутке каждый множитель есть разность двух неотрицательных чисел, а следовательно, можно воспользоваться методом замены множителей. Итак, имеем
Слайд 13Показательная и логарифмическая функция
и вызываемые ею замены
Показательная функция
и строго возрастает при . Поэтому, в частности для получаем
Для произвольного основания a, пользуясь основным логарифмическим тождеством, можно увидеть, что
Откуда
(11)
Слайд 14Функция - строго
Если x1=a и x2=1, то получаем, что
(12)
Откуда соотношение (11) принимает вид
(13)
Таким образом, мы установили, что разность степеней с одним и тем же основанием всегда по знаку совпадает с произведением разности показателей этих степеней на разность основания и единицы.
Слайд 15Для логарифмической функции
Отсюда следует, что
То есть разность логарифмов по одному и тому же основанию всегда по знаку совпадает с отношением разности подлогарифмических выражений к разности основания и единицы:
(14)
Слайд 16Замечание. Утверждения (14) и (13) равносильны, поскольку показательная и логарифмическая функции
Эти утверждения также позволяют исключительно эффективно решать очень многие неравенства, которые принято относить к разряду задач повышенной сложности. В частности из (13) и (14) следуют полезные схемы решения основных показательных логарифмических неравенств:
1)
2)
Слайд 53I. Стандартный вид неравенств, когда применяется метод замены множителей
где символ «∨»
Слайд 54II. Основная идея метода замены множителей состоит в замене любого множителя
Замечание. Преобразованное таким образом неравенство всегда равносильно исходному в области существования последнего.
Предупреждение. Указанная замена возможна только тогда, когда неравенство приведено к стандартному виду
Слайд 55III. Две основные замены:
если f(t) – строго возрастающая функция;
если f(t) –
Слайд 60ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА
Голубев В. И. Метод замены множителей, М: Архимед. Лекции и
Голубев В. И., Шарыгин И.Ф. Эффективный путь решения неравенств М. Квантор 1993 г.