- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод областей и его обобщенияпри решении неравенств с двумя переменными презентация
Содержание
- 1. Метод областей и его обобщенияпри решении неравенств с двумя переменными
- 2. Содержание Графическое решение неравенств Cвойство чередования знака
- 3. Графическое решение неравенств Решением неравенства с двумя
- 4. Решить неравенство – значит найти множество
- 5. Полезно будет напомнить здесь одно простое
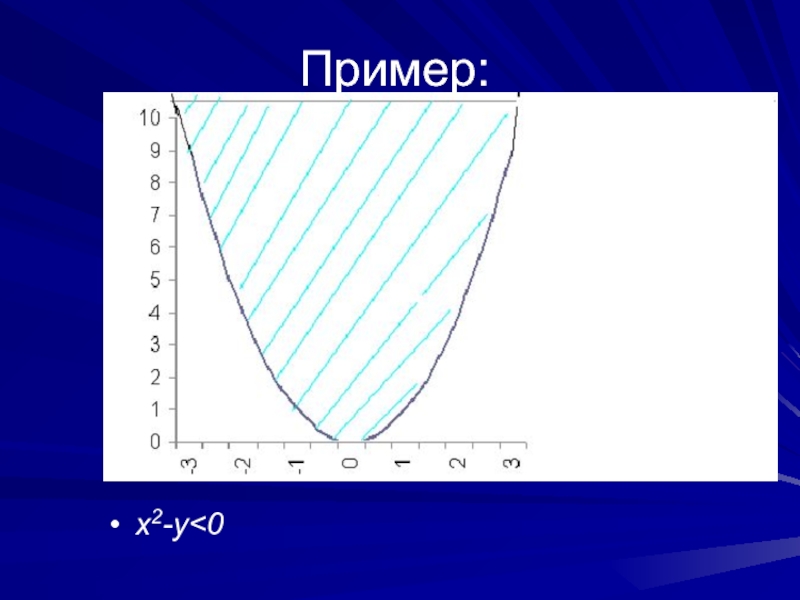
- 6. Пример: x2-y
- 7. Cвойство чередования знака для линейного многочлена F(x;y)=
- 8. Метод областей и его обобщения
- 9. Области знакопостоянства многочленов F(x;y) второй степени Теорема:
- 10. Теорема: Парабола, заданная каноническим уравнением y2=
- 11. Примеры Пример 1. Показать штриховкой на
- 12. Записать неравенство, которое задает множество точек
- 13. Пример 2. Найдите на координатной плоскости
- 14. Спасибо за внимание!
Слайд 2Содержание
Графическое решение неравенств
Cвойство чередования знака для линейного многочлена F(x;y)= px +
qy + r(p2 + q2 = 0)
Метод областей и его обобщения
Области знакопостоянства многочленов F(x;y) второй степени
примеры
Метод областей и его обобщения
Области знакопостоянства многочленов F(x;y) второй степени
примеры
Слайд 3Графическое решение неравенств
Решением неравенства с двумя переменными F(x;y)>0 называется упорядоченная пара
действительных чисел (x0;y0), обращающая это неравенство в верное числовое неравенство.
Графически это соответствует заданию точки (x0;y0) координатной плоскости.
Графически это соответствует заданию точки (x0;y0) координатной плоскости.
Слайд 4
Решить неравенство – значит найти множество всех его решений.
Совокупность всех
точек, координаты которых удовлетворяют неравенству F(x;y)>0 , называют областью его решений.
Неравенства называются равносильными, если они имеют одну и ту же область решений.
Неравенства называются равносильными, если они имеют одну и ту же область решений.
Слайд 5
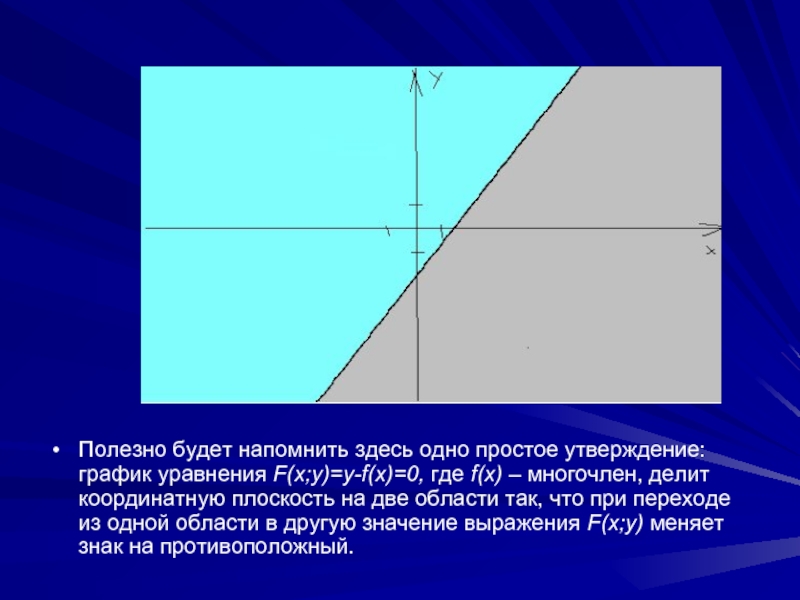
Полезно будет напомнить здесь одно простое утверждение: график уравнения F(x;y)=y-f(x)=0, где
f(x) – многочлен, делит координатную плоскость на две области так, что при переходе из одной области в другую значение выражения F(x;y) меняет знак на противоположный.
Слайд 7Cвойство чередования знака для линейного многочлена F(x;y)= px + qy +
r(p2 + q2 = 0):
При переходе через точку прямой px + qy + r = 0 из одной полуплоскости в другую знак значения многочлена F(x;y) меняется на противоположный.
Слайд 8Метод областей и его обобщения
Метод областей опирается на следующее свойство
чередования знака выражения 1) F(x;y) = F1(x;y)*F2(x;y)*…*Fn(x;y) :
При переходе через обыкновенную точку прямой pix + qiy + ri = 0 (границы области) из одной области в смежную знак значения выражения (1) меняется на противоположный.
При переходе через обыкновенную точку прямой pix + qiy + ri = 0 (границы области) из одной области в смежную знак значения выражения (1) меняется на противоположный.
Слайд 9Области знакопостоянства многочленов F(x;y) второй степени
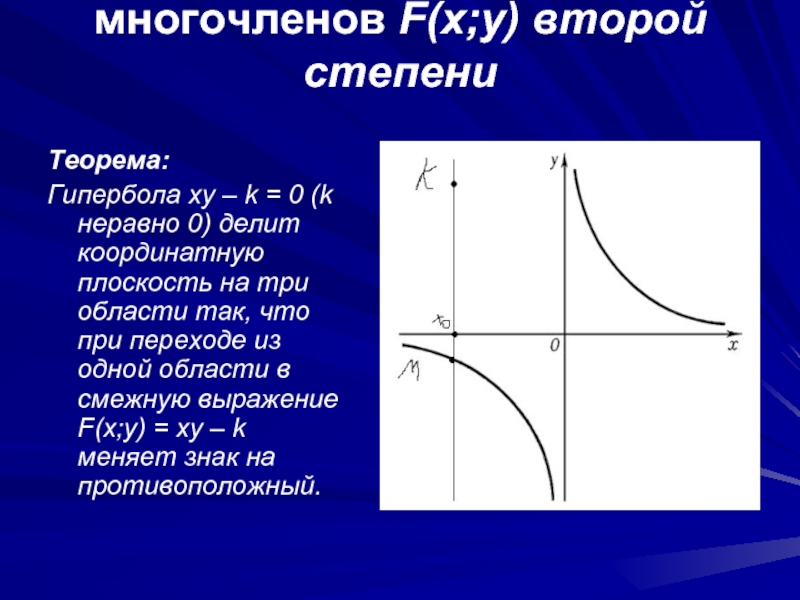
Теорема:
Гипербола xy – k = 0
(k неравно 0) делит координатную плоскость на три области так, что при переходе из одной области в смежную выражение F(x;y) = xy – k меняет знак на противоположный.
Слайд 10
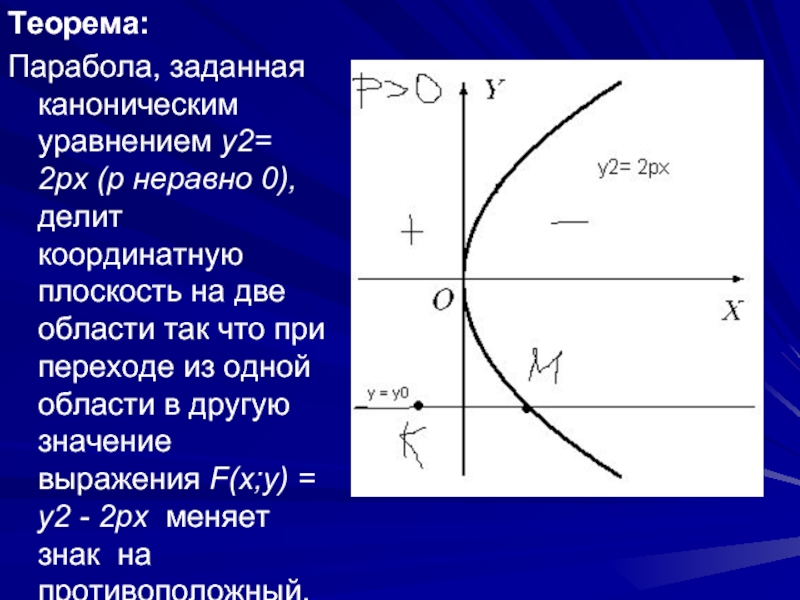
Теорема:
Парабола, заданная каноническим уравнением y2= 2px (p неравно 0), делит координатную
плоскость на две области так что при переходе из одной области в другую значение выражения F(x;y) = y2 - 2px меняет знак на противоположный.
Слайд 11Примеры
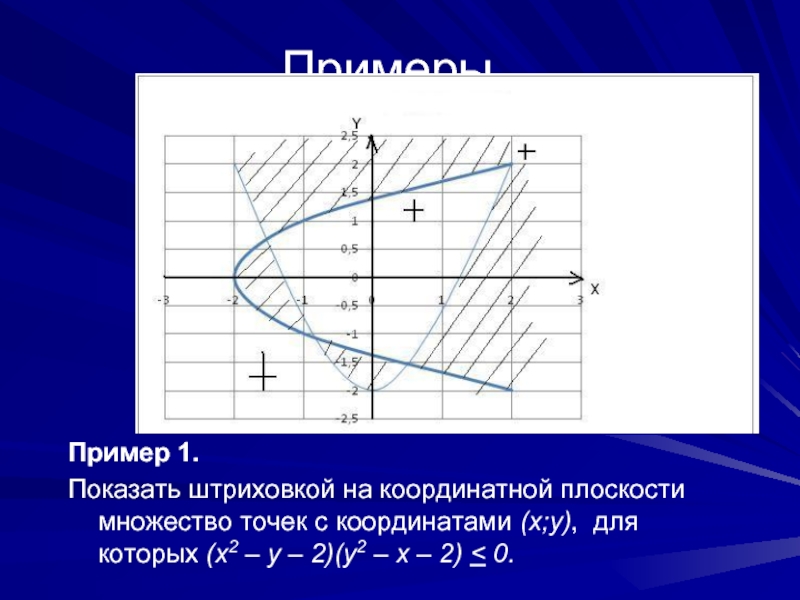
Пример 1.
Показать штриховкой на координатной плоскости множество точек с координатами
(x;y), для которых (x2 – y – 2)(y2 – x – 2) < 0.
Слайд 12
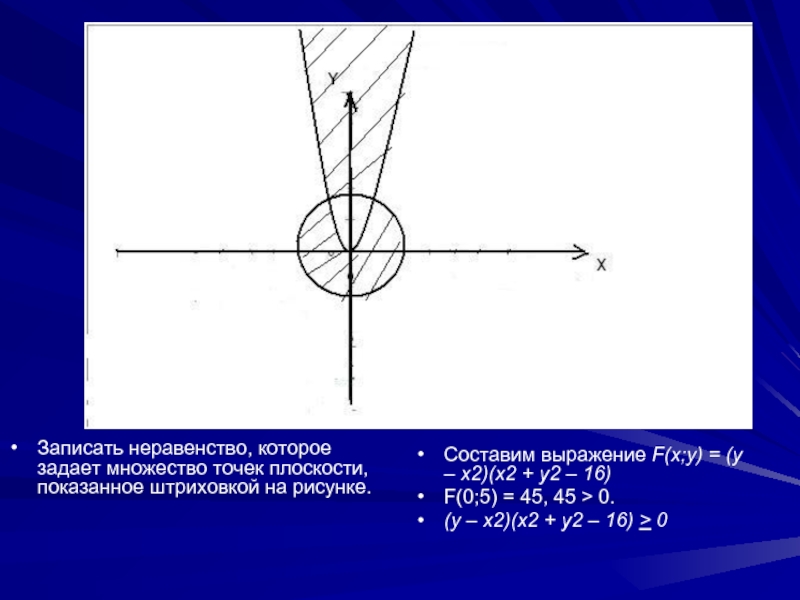
Записать неравенство, которое задает множество точек плоскости, показанное штриховкой на рисунке.
Составим
выражение F(x;y) = (y – x2)(x2 + y2 – 16)
F(0;5) = 45, 45 > 0.
(y – x2)(x2 + y2 – 16) > 0
F(0;5) = 45, 45 > 0.
(y – x2)(x2 + y2 – 16) > 0
Слайд 13
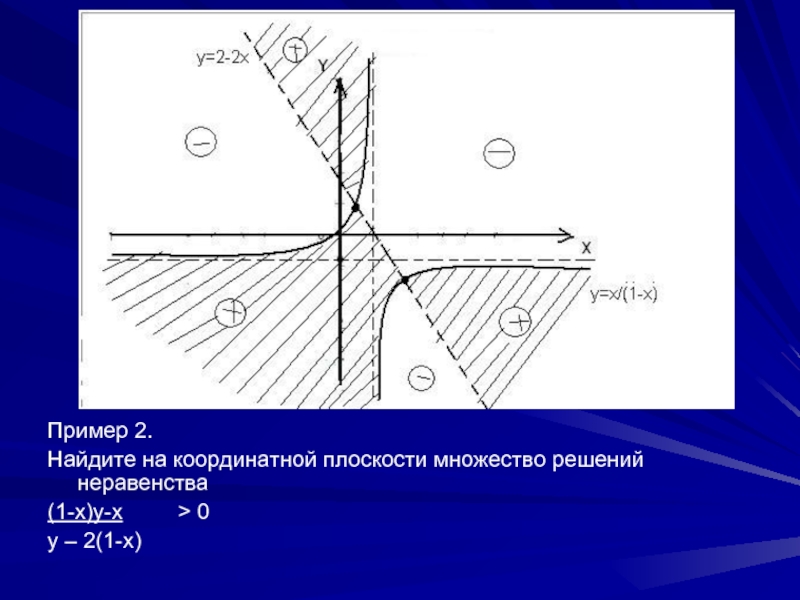
Пример 2.
Найдите на координатной плоскости множество решений неравенства
(1-x)y-x
> 0
y – 2(1-x)
y – 2(1-x)