- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Метод областей презентация
Содержание
- 1. Метод областей
- 2. Определение Метод областей – это аналог метода
- 3. Задача В координатной плоскости переменных х и
- 4. Решение Первый шаг. Построение границ.
- 5. Решение Прямая и парабола в
- 6. Решение Для выявления конкретной
- 7. Второй шаг. Определение знака в областях.
- 8. Способ Ι– прямой счет.
- 9. Решением задачи является заштрихованная область.
- 10. Способ II- аналитический.
- 11. Очевидно, что относительно
- 12. При всех значениях параметра а решить неравенство
- 19. Ответ: при а -1, х є(- ;-а)U(1;+ ).
Слайд 2Определение
Метод областей – это аналог метода интервалов решения неравенств с одной
переменной при решении неравенств с двумя переменными.
Слайд 3Задача
В координатной плоскости переменных х и р изобразить множество всех точек
плоскости, координаты которых удовлетворяют неравенству:
(р-х2)(р+х-2)<0 (1)
(р-х2)(р+х-2)<0 (1)
Слайд 4Решение
Первый шаг. Построение границ.
(р-х2)(р+х-2)=0 ‹=›
‹=› р-х2=0 или р+х-2=0 ‹=›
‹=› р=х2 или р=2-х.
Первое равенство в плоскости (х;р) задает параболу, а второе – прямую. Как парабола, так и прямая разбивает плоскость (х;р) на две области. Для всех точек каждой области соответствующий множитель левой части неравенства (1) имеет фиксированный знак, который необходимо впоследствии определить.
‹=› р-х2=0 или р+х-2=0 ‹=›
‹=› р=х2 или р=2-х.
Первое равенство в плоскости (х;р) задает параболу, а второе – прямую. Как парабола, так и прямая разбивает плоскость (х;р) на две области. Для всех точек каждой области соответствующий множитель левой части неравенства (1) имеет фиксированный знак, который необходимо впоследствии определить.
Слайд 5Решение
Прямая и парабола в зависимости от взаимного расположения разбивают
плоскость на области в количестве от трех до пяти:
три области, если прямая не пересекает параболу;
четыре области, если прямая касается параболы, либо параллельна оси параболы;
пять областей, если прямая пересекает параболу в двух точках.
три области, если прямая не пересекает параболу;
четыре области, если прямая касается параболы, либо параллельна оси параболы;
пять областей, если прямая пересекает параболу в двух точках.
Слайд 6Решение
Для выявления конкретной ситуации необходимо найти общие точки
параболы и прямой или доказать, что они не существуют.
То есть нам нужно решить данную систему уравнений р-х2=0
р+х-2=0
Очевидно, что данная система имеет два решения, то есть определяет две точки, в которых прямая пересекает параболу, и таким образом задает пять различных областей.
То есть нам нужно решить данную систему уравнений р-х2=0
р+х-2=0
Очевидно, что данная система имеет два решения, то есть определяет две точки, в которых прямая пересекает параболу, и таким образом задает пять различных областей.
Слайд 7
Второй шаг. Определение знака в областях.
Существуют два основных способа
определения знака множителя ( или всего произведения):
- способ прямого определения путем вычисления значения множителя для координат выбранной точки из данной плоскости.
- аналитический способ.
- способ прямого определения путем вычисления значения множителя для координат выбранной точки из данной плоскости.
- аналитический способ.
Слайд 8
Способ Ι– прямой счет.
Парабола задает все точки плоскости,
в которых множитель р-х2=0, и разбивает плоскость на две части- внутреннюю и внешнюю. Для внутренней части точки (0;1) множитель р-х2=1>0, а для внешней части точки (1;0) множитель р-х2=-1<0. Следовательно для всех точек внутренней части р-х2>0, а для всех точек внешней части р-х2<0, что отмечаем знаками «+» и «-» на соответствующих сторонах ветвей параболы. Совершенно аналогично устанавливается знак множителя р+х-2 в двух полуплоскостях относительно прямой, что также отмечается знаками «+» и «-» около прямой.
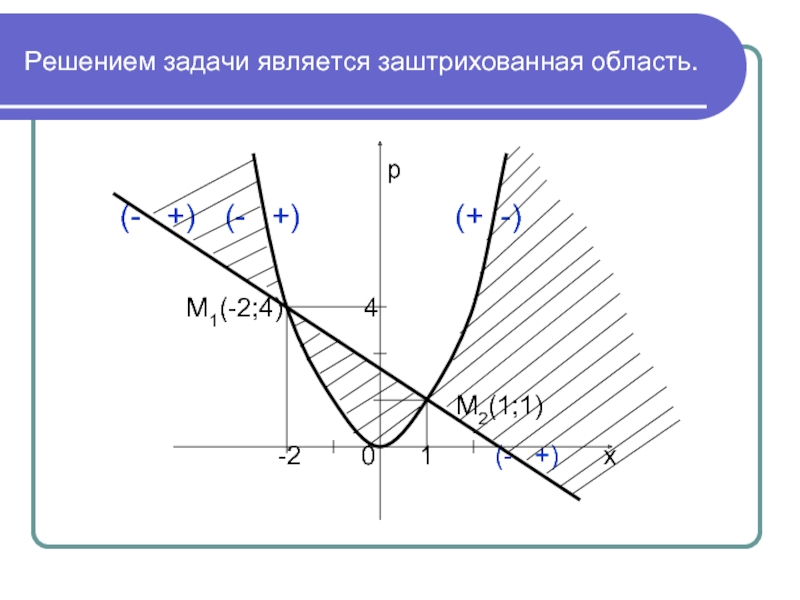
Слайд 9Решением задачи является заштрихованная область.
р
(- +) (- +) (+ -)
М1(-2;4) 4
М2(1;1)
-2 0 1 (- +) х
(- +) (- +) (+ -)
М1(-2;4) 4
М2(1;1)
-2 0 1 (- +) х
Слайд 10
Способ II- аналитический.
Как и ранее будем определять знаки
в областях, задаваемым одним множителем.
Точки в которых первый множитель р-х2=0 есть парабола, разделяющая плоскость координат х и р на две части. Из точки на границе р-х2=0 можно двигаться в любую их областей и следить, как величина р-х2 изменяется. В любую точку каждой из двух областей можно прийти либо по вертикали, либо по горизонтали, начиная движение из соответствующей точки границы (параболы).Указанные направления «движения» выбраны с тем, чтобы не изменять значение одной из переменных х или р.
Точки в которых первый множитель р-х2=0 есть парабола, разделяющая плоскость координат х и р на две части. Из точки на границе р-х2=0 можно двигаться в любую их областей и следить, как величина р-х2 изменяется. В любую точку каждой из двух областей можно прийти либо по вертикали, либо по горизонтали, начиная движение из соответствующей точки границы (параболы).Указанные направления «движения» выбраны с тем, чтобы не изменять значение одной из переменных х или р.
Слайд 11
Очевидно, что относительно переменной р выражение р-х2 как
функция является линейной, а относительно х – квадратичной. Поэтому легче, зафиксировав переменную х, отслеживать изменения величины р-х2 в зависимости от р. Это значит, что мы будем двигаться вдоль вертикальных прямых х=х0.
Если из точки параболы р-х2=0 мы смещаемся вверх по вертикальной прямой во внутреннюю область, то ордината р будет увеличиваться, т.е. уменьшаемое в разности р-х2 будет возрастать. Следовательно, от значения, равного нулю, множитель р-х2 будет переходить к положительным значениям. И как мы уже говорили, двигаясь по вертикальной прямой, параметр р возрастает для всех точек внутренней области р-х2 > 0 и параметр р убывает для всех точек внешней области р-х2 < 0.
Для множителя р+х-2 проводятся аналогичные рассуждения.
Если из точки параболы р-х2=0 мы смещаемся вверх по вертикальной прямой во внутреннюю область, то ордината р будет увеличиваться, т.е. уменьшаемое в разности р-х2 будет возрастать. Следовательно, от значения, равного нулю, множитель р-х2 будет переходить к положительным значениям. И как мы уже говорили, двигаясь по вертикальной прямой, параметр р возрастает для всех точек внутренней области р-х2 > 0 и параметр р убывает для всех точек внешней области р-х2 < 0.
Для множителя р+х-2 проводятся аналогичные рассуждения.
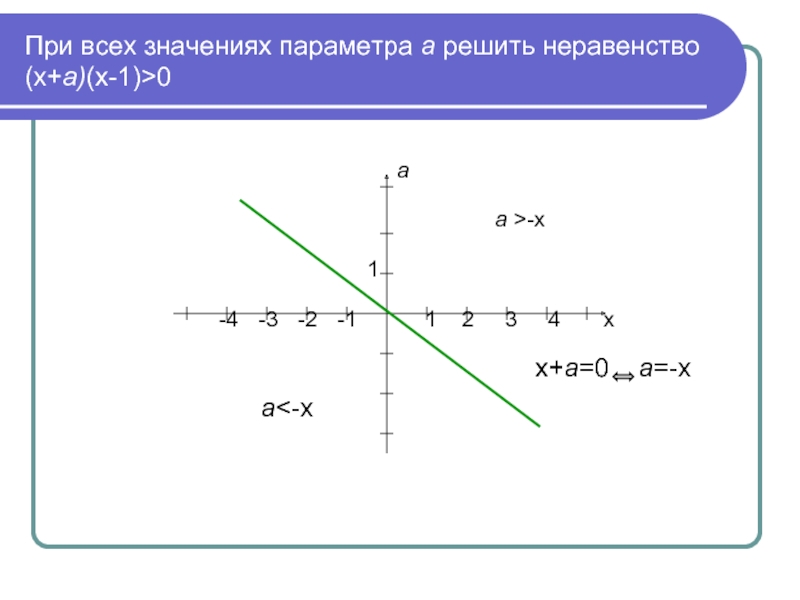
Слайд 12При всех значениях параметра а решить неравенство
(х+а)(х-1)>0
а
а >-х
1
-4 -3 -2 -1 1 2 3 4 х
х+а=0 а=-х
а<-х
а >-х
1
-4 -3 -2 -1 1 2 3 4 х
х+а=0 а=-х
а<-х
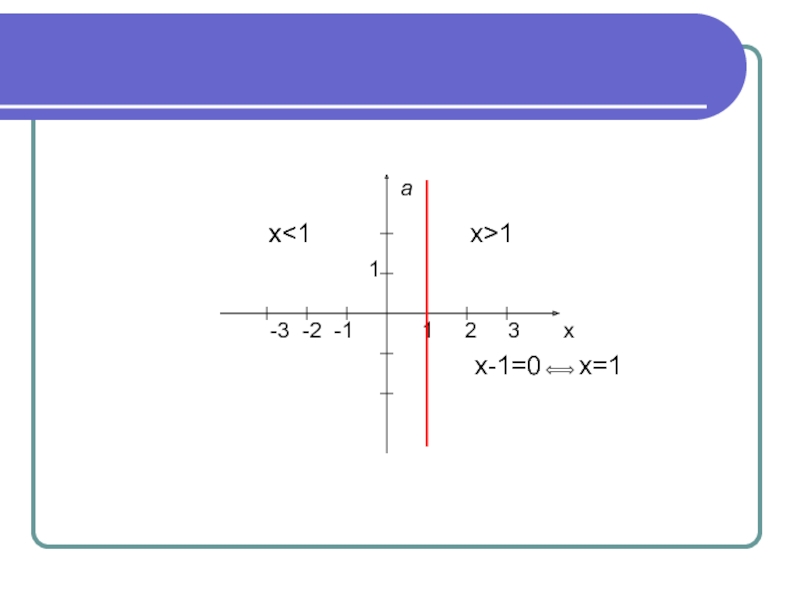
Слайд 16
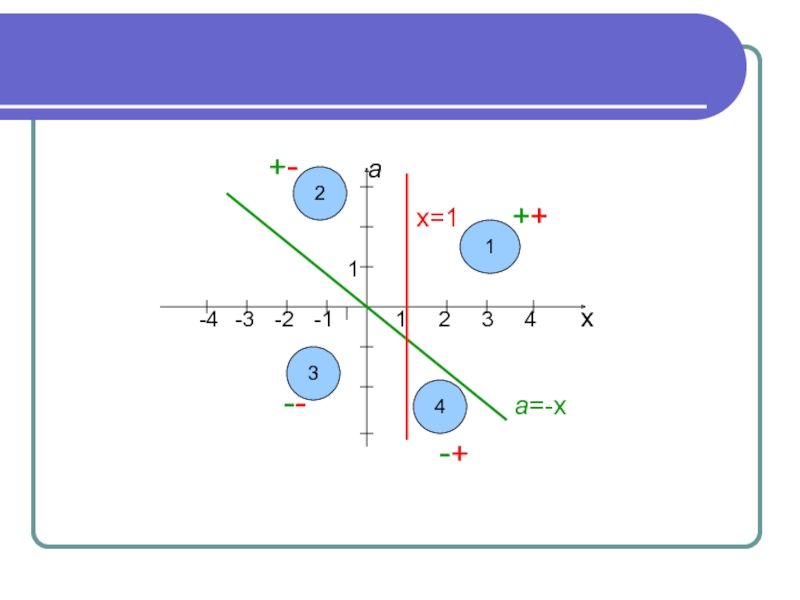
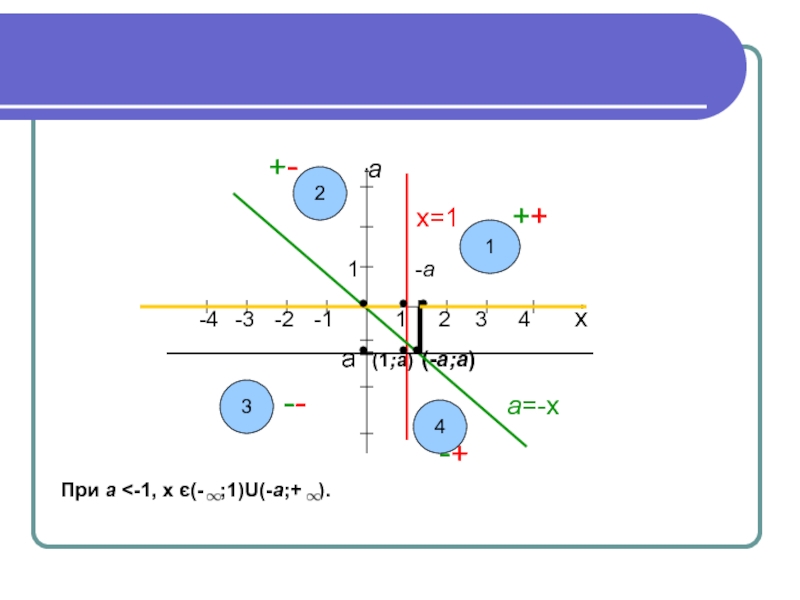
+- а
х=1 ++
1 -а
-4 -3 -2 -1 1 2 3 4 х
а (1;а) (-а;а)
-- а=-х
-+
При а <-1, х є(- ;1)U(-а;+ ).
х=1 ++
1 -а
-4 -3 -2 -1 1 2 3 4 х
а (1;а) (-а;а)
-- а=-х
-+
При а <-1, х є(- ;1)U(-а;+ ).
2
3
4
1
Слайд 17
+- а
х=1 ++
1 -а
-4 -3 -2 -1 -1 а 1 2 3 4 х
(-1;1)
-- а=-х
-+
При а =-1, хє(- ;1)U(1;+ ).
х=1 ++
1 -а
-4 -3 -2 -1 -1 а 1 2 3 4 х
(-1;1)
-- а=-х
-+
При а =-1, хє(- ;1)U(1;+ ).
2
3
4
1
Слайд 18
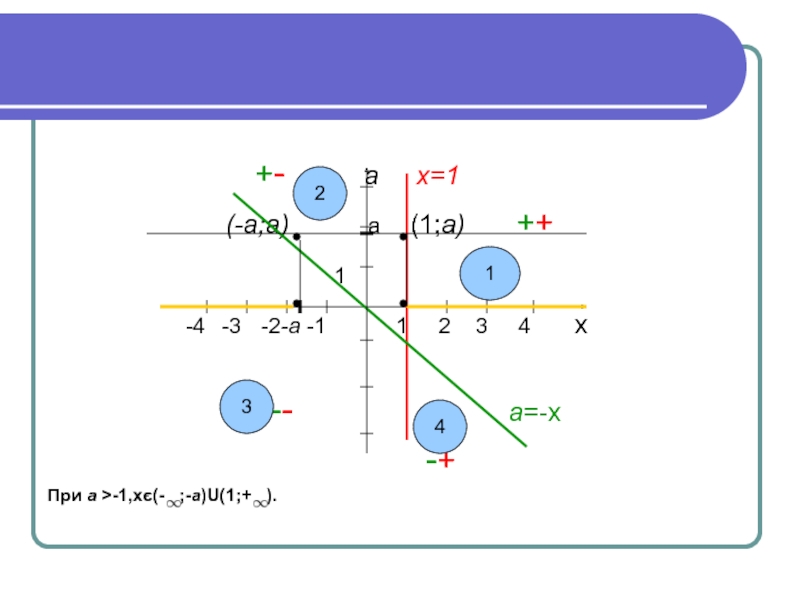
+- а х=1
(-а;а) а (1;а) ++
1
-4 -3 -2-а -1 1 2 3 4 х
-- а=-х
-+
При а >-1,хє(- ;-а)U(1;+ ).
(-а;а) а (1;а) ++
1
-4 -3 -2-а -1 1 2 3 4 х
-- а=-х
-+
При а >-1,хє(- ;-а)U(1;+ ).
2
3
4
1