- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Масловский Филипп презентация
Содержание
- 1. Масловский Филипп
- 2. Тема работы: История развития комбинаторики и применение её в формулах алгебры
- 3. Цель исследования: ИССЛЕДОВАТЬ СПОСОБ ВЫЧИСЛЕНИЯ БИНОМИАЛЬНЫХ
- 4. В теории вероятностей изучаются реально существующие независимо
- 5. Предыстория развития знаний по комбинаторике.
- 6. Средневековье. Как научная дисциплина, комбинаторика сформировалась в
- 7. Развитие теории вероятностей, а с нею и
- 8. Следующий период начинается с появления работы Я.
- 9. \ Термин "комбинаторика" был введён в математический
- 10. Основные формулы комбинаторики Для успешного
- 11. Правило 2. Правило произведения. Пример. В
- 12. Формулы комбинаторики. Формула размещения. Если комбинации из
- 13. Формула сочетания. Если комбинации из n элементов
- 14. Формула перестановки. Если комбинации из n элементов
- 15. Применение комбинаторики в формулах алгебры. (a+b)n –
- 16. Коэффициенты разложения можно представить в виде
- 17. Арифметический треугольник позволяет найти любой биномиальный коэффициент,
- 18. С помощью этой формулы можно вычислить любой
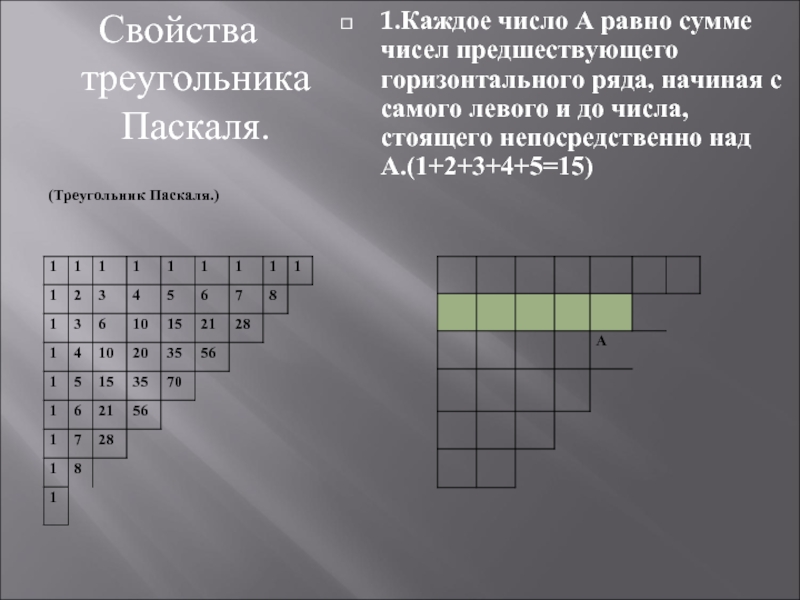
- 19. Свойства треугольника Паскаля. 1.Каждое число А равно
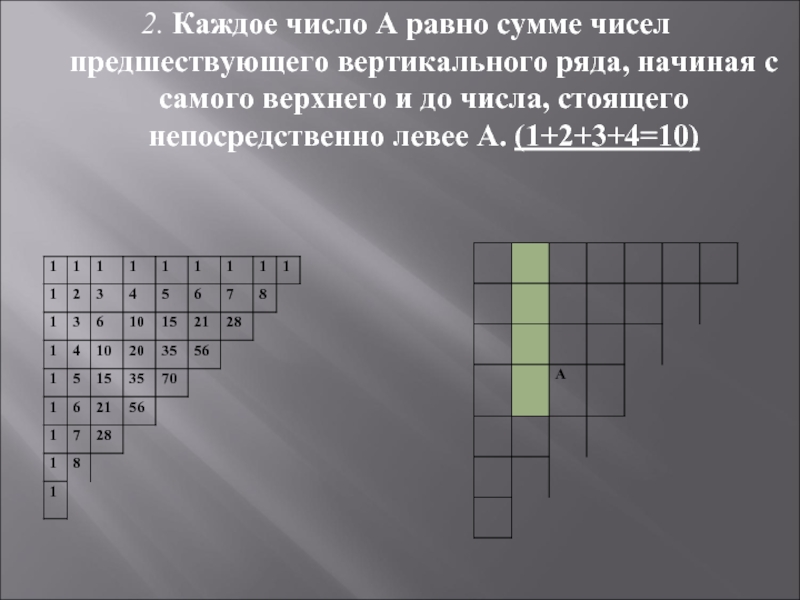
- 20. 2. Каждое число А равно сумме чисел
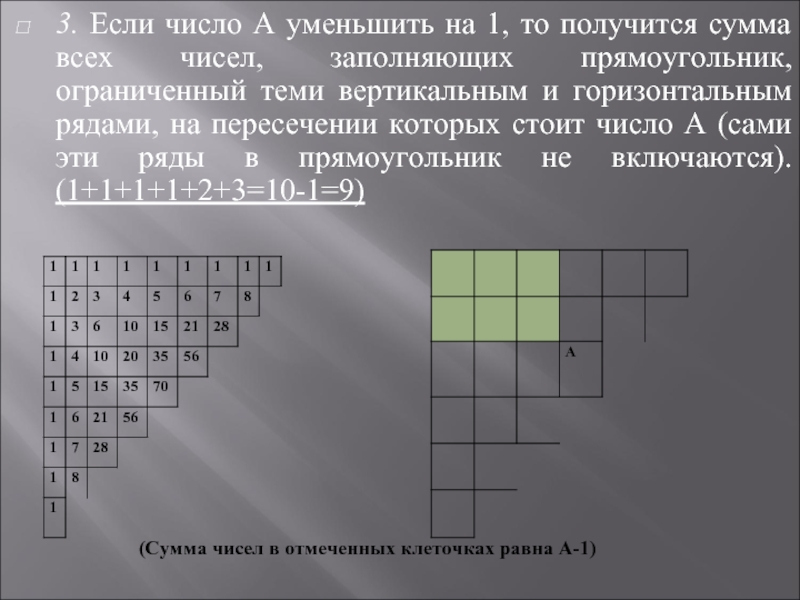
- 21. 3. Если число А уменьшить на 1,
- 22. Заключение В заключение хотелось бы еще раз
- 23. Спасибо за внимание
Слайд 3Цель исследования:
ИССЛЕДОВАТЬ СПОСОБ ВЫЧИСЛЕНИЯ БИНОМИАЛЬНЫХ КОЭФФИЦИЕНТОВ С ПОМОЩЬЮ
ЗАДАЧИ:
1. Изучить историю возникновения комбинаторики как науки.
2. Определить основные правила и формулы комбинаторики.
3. Рассмотреть свойства расположения биномиальных коэффициентов разложения в треугольнике Паскаля.
Слайд 4В теории вероятностей изучаются реально существующие независимо от нашего сознания законы
Слайд 5
Предыстория развития знаний по комбинаторике.
Комбинаторные мотивы можно заметить в
Элементы комбинаторики так же были известны в Индии еще во II в. до н. э. Идийцы умели вычислять числа, которые сейчас называют "сочетания".
Слайд 6Средневековье.
Как научная дисциплина, комбинаторика сформировалась в XVII в. Б. Паскаль в
Слайд 7Развитие теории вероятностей, а с нею и комбинаторики.
В этот период, начало
Д. Кардано
Н. Тарталья
Слайд 8Следующий период начинается с появления работы Я. Бернулли "Искусство предположений" (1713),
В центре внимания в это время стоят предельные теоремы. Теория вероятностей начинает широко применяться в различных областях естествознания. И хотя в этот период начинают применяться различные понятия вероятности (геометрическая вероятность, статистическая вероятность), господствующее положение занимает, в особенности после работ Лапласа, так называемое классическое определение вероятности.
Я. Бернулли
Слайд 9\
Термин "комбинаторика" был введён в математический обиход знаменитым Лейбницем. Готфрид Вильгельм
В 1666 году Лейбниц опубликовал "Рассуждения о комбинаторном искусстве". В своём сочинении Лейбниц, вводя специальные символы, термины для подмножеств и операций над ними находит все k -сочетания из n элементов выводит свойства сочетаний:
Вильгельм Лейбниц
Слайд 10
Основные формулы комбинаторики
Для успешного решения комбинаторных задач необходимо знать два правила
Правило 1. Правило суммы.
Пример. В ящике 300 деталей. Известно, что 150 из них – 1-го сорта, 120 – 2-го, а остальные – 3-го сорта. Сколько существует способов извлечения из ящика одной детали 1-го или 2-го сорта?
Решение. Деталь 1-го сорта может быть извлечена 150 способами, 2-го сорта может быть извлечена 120 способами. По правилу суммы существует +=150+120=270 способов извлечения. Одной детали 1-го или 2-го сорта.
Слайд 11
Правило 2. Правило произведения.
Пример. В группе 30 человек. Необходимо выбрать старосту,
Решение. Старостой может быть выбран любой из 30 учащихся, его заместитель – любой из оставшихся 29, а физоргом – любой из оставшихся 28 учащихся, т.е. По правилу произведения общее число способов выбора старосты, его заместителя и физорга равно способов.
n1n2…nk=30.29.28=24360 способов.
Слайд 12Формулы комбинаторики.
Формула размещения.
Если комбинации из n элементов по m отличаются либо
Пример. Расписание одного дня состоит из 5 уроков. Определить число вариантов расписания при выборе из 11 дисциплин.
Решение. Каждый вариант расписания представляет набор 5 дисциплин из 11, отличающихся от других вариантов как составом дисциплин, так и порядком их следования (или и тем и другим), т.е. является размещением из 11 элементов по 5 . Число вариантов расписаний, т.е. число размещений из 11 по 5, находим по формуле…
Слайд 13Формула сочетания.
Если комбинации из n элементов по m отличаются только составом
Пример. В шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?
Решение. Каждая партия играется двумя участниками из 16 и отличается от других только составом пар участников, т.е. представляет собой сочетание из 16 элементов по 2. Их число находим по формуле:
Слайд 14Формула перестановки.
Если комбинации из n элементов по m отличаются только порядком
Пример. Порядок выступления 7 участников конкурса определяется жребием. Сколько различных вариантов жеребьёвки при этом возможно?
Решение. Каждый вариант жеребьёвки отличается только порядком участников конкурса, т.е. является перестановкой из 7 элементов. Их число по формуле:
Слайд 15Применение комбинаторики в формулах алгебры.
(a+b)n – это произведение n сомножителей, каждый
Слайд 16Коэффициенты разложения можно представить в виде треугольника Паскаля, хотя
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
Блез Паскаль
Слайд 17Арифметический треугольник позволяет найти любой биномиальный коэффициент, но при больших значениях
Оказывается можно:
Cnk= =
Эту формулу и вывел
Исаак Ньютон
Слайд 18С помощью этой формулы можно вычислить любой биномиальный коэффициент.
Для примера
(a+b)10=a10+10a9b+45a8b2+120a7b3+210a6b4+252a5b5+210a4b6+120a3b7+45a2b8+10ab9+b10.
Слайд 19Свойства треугольника Паскаля.
1.Каждое число А равно сумме чисел предшествующего горизонтального ряда,
(Треугольник Паскаля.)
Слайд 202. Каждое число А равно сумме чисел предшествующего вертикального ряда, начиная
Слайд 213. Если число А уменьшить на 1, то получится сумма всех
(Сумма чисел в отмеченных клеточках равна А-1)