- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Логарифмическая функция презентация
Содержание
- 1. Логарифмическая функция
- 2. Обобщение свойств логарифмической функции. Выделение
- 3. Этапы урока Воспроизведение повторяемого материала.
- 4. | Этап Построение графиков функций:
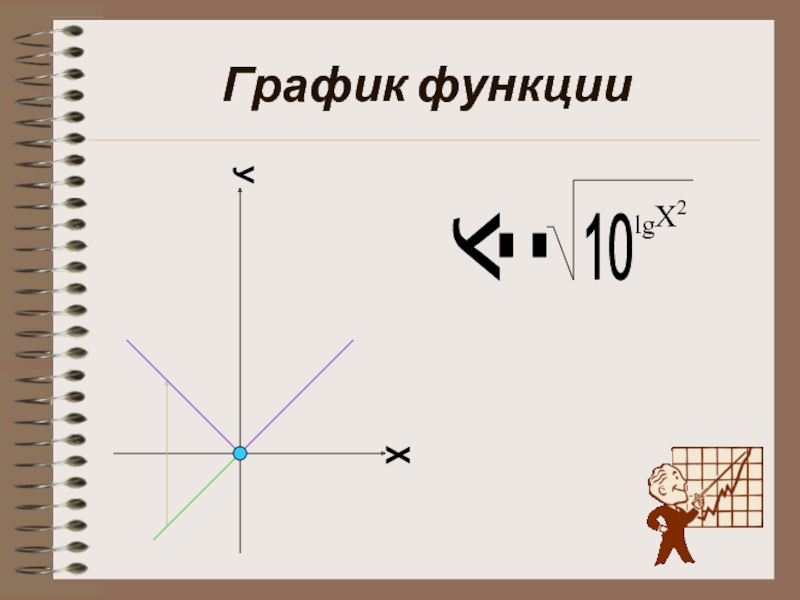
- 5. График функции y = 10 lg X2 х у
- 6. Функция У
- 7. График функции у х
- 8. || Этап Делай, что можешь с
- 9. Функция У = log3 (X2 –9)/(|Х|-3)
- 10. Анализ выражения, стоящего под знаком логарифма
- 11. График функции У = log3(Х+3) 3
- 12. ||| Этап …Лучше знать лишнее, чем ничего
- 13. График функции У = |log2(X – 4)
- 14. |V Этап Приобретать познания ещё недостаточно
Слайд 2 Обобщение свойств логарифмической функции.
Выделение понятия области определения и
Установление связей с наиболее трудными вопросами теории.
Расширение класса функций, графики которых можно построить с помощью преобразований.
Цели урока
y = log a x
y = log a (x + 4)
y = | log a x |
Слайд 3Этапы урока
Воспроизведение повторяемого материала.
Систематизация и обобщение ранее изученного.
Углубление
Проверка усвояемости изученного материала.
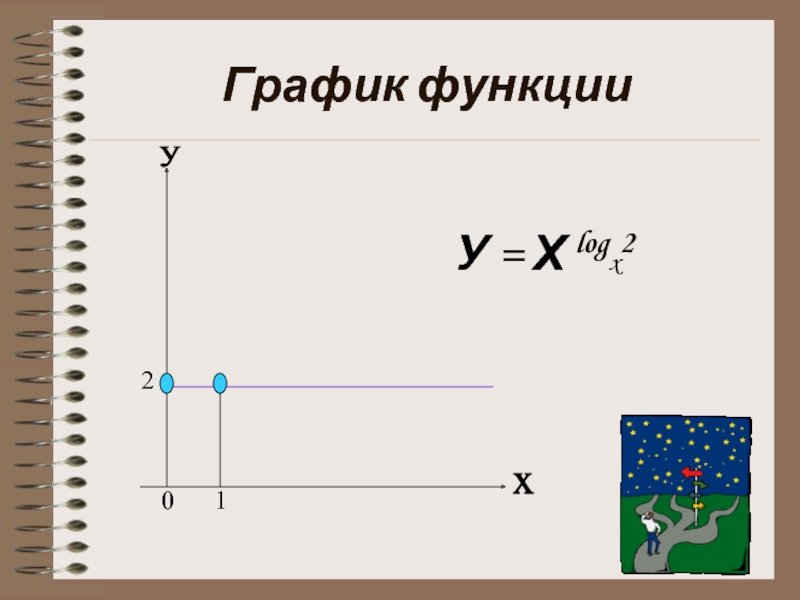
Слайд 6 Функция У = Х logx2
Свойства
D(y) = (0;1) u (1; )
a
=
M
logaM
У = Х logx2 = 2
Слайд 8|| Этап
Делай, что можешь с тем, что у тебя есть,
Теодор Рузвельт.
Построение графика функции
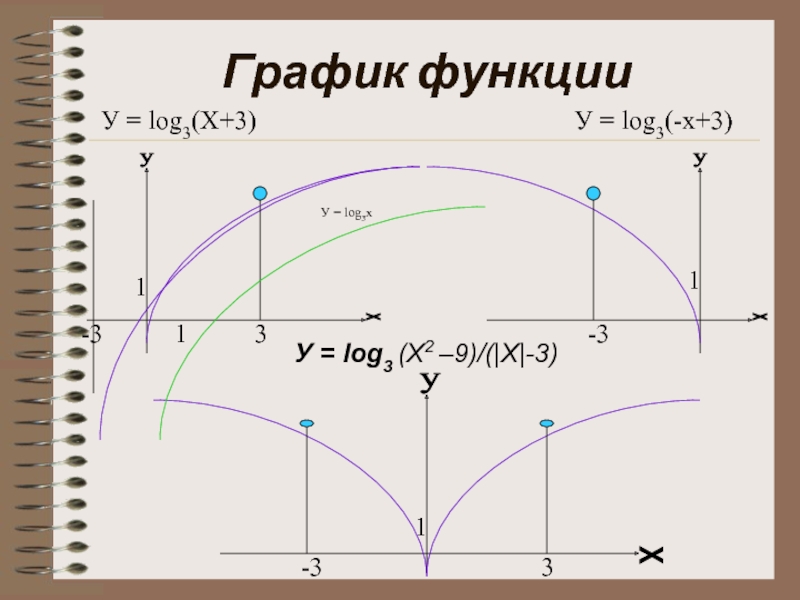
У = log3 (X2 –9)/(|Х|-3)
Слайд 9Функция У = log3 (X2 –9)/(|Х|-3)
Функция чётная –
график симметричен
Расшифровка выражения.
Х, если Х > 0
-Х, если Х < 0
|X| =
Слайд 10Анализ выражения, стоящего под знаком логарифма
Х > 0.
(Х2 –
Вывод: функция принимает вид y = log3(x+3) в первом случае и y = log3(-x + 3) во втором случае.
Х < 0.
(Х2 – 9) / (-Х-3) > 0 при Х из [- ; -3)U(-3; 0].
Слайд 11График функции
У = log3(Х+3)
3
1
1
-3
х
х
х
у
у
у
1
-3
3
У = log3 (X2 –9)/(|Х|-3)
1
У = log3x
-3
Слайд 12||| Этап
…Лучше знать лишнее, чем ничего не знать.
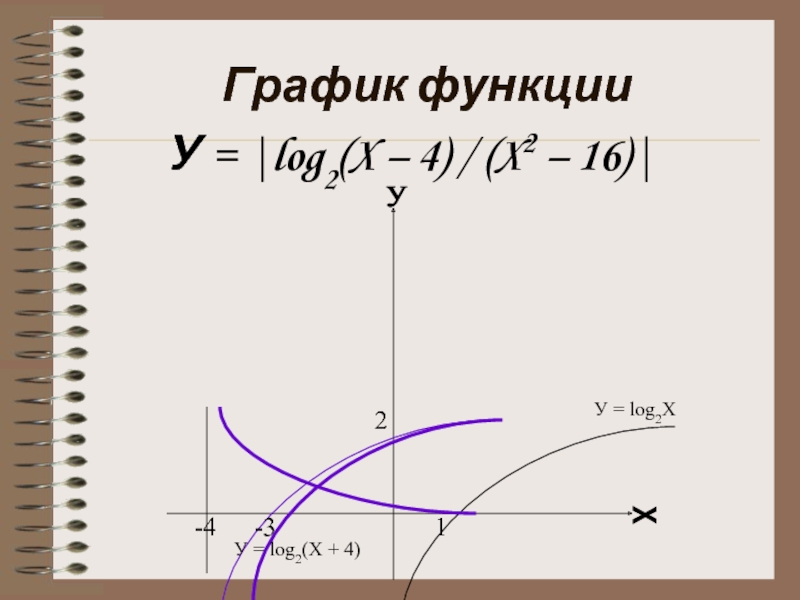
Построение графика функции
У = |log2(X – 4) / (X2 – 16)|
Слайд 14|V Этап
Приобретать познания ещё недостаточно для человека, надо уметь отдавать
Самостоятельная работа
Построить график функции
1-ый вариант 2-ой вариант
3-ий вариант 4-ый вариант
У = log3(X2 – 4)/(|X| +2) У = |log2(X – 2)/(X2 – 4)|
У = log3(X + 5) У =| log3(X + 5) |
Ж е л а ю у с п е х а!