високих технологій
Київського національного університету імені Тараса Шевченка
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Контакт метал - напівпровідник презентация
Содержание
- 1. Контакт метал - напівпровідник
- 2. Ідеальна модель і поверхневі стани Зонні енергетичні
- 3. Збіднений шар Зонні енергетичні діаграми контактів метала
- 4. Рівняння Пуасона: 2=-/0s Різкий несиметричний p-n перехід;
- 5. Питома ємність збідненого шару Якщо концентрація ND
- 6. Ефект Шотткі Енергетична діаграма системи метал-вакуум. Ефективна
- 7. Зниження енергетичного бар’єра як функція електричного поля
- 8. Теорія процесів переносу заряда Чотири основні процеси
- 9. 1. Теорія термоелектронної емісії. Припущення: 1. Висота
- 10. 2. Дифузійна теорія Припущення: 1. Висота бар’єру
- 11. Розподіл потенціалу в бар’єрі Шотткі: JSD
- 12. 3. Термоемісійна- дифузійна теорія. Енергетична діаграма контакту
- 13. Якщо vD>>vR, то передекспоненційному члені залишається лише vR і справедлива теорія термоелектронної емісії. Якщо vD
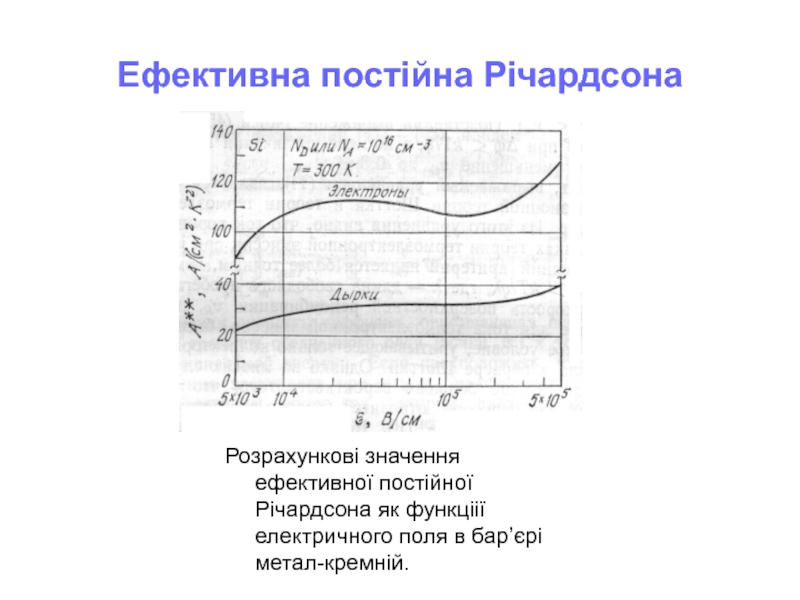
- 14. Ефективна постійна Річардсона Розрахункові значення ефективної постійної Річардсона як функціії електричного поля в бар’єрі метал-кремній.
- 15. 4. Тунельний струм Дві компоненти струму: термоелектронна
- 16. Залежності густини струму насичення (а) и фактору
- 17. 5. Інжекція неосновних носіїв. Енергетична діаграма епітаксійного
- 18. Висота бар’єра Детальна енергетична діаграма контакту метал-напівпровідник
- 19. Висота бар’єра Два припущення: 1.Товщина проміжного шару
- 20. Вирішуємо відносно Bn і отримуємо: де При s100, i=0 і ND
- 21. Два граничні випадки: 1. Якщо Ds
- 22. Виміри висоти бар’єру. 1. Метод вольт-амперної характеристики
- 23. 2. Метод енергії активації. Залежність струму від
- 24. 3. Метод вольт-фарадної характеристики Залежність 1/C2 від
- 25. Якщо концентрація ND постійна у всій області
- 26. 4. Фотоелектричний метод. Принципова схема установки для
- 27. Теорія Фаулера. Залежність квантового виходу R від
- 28. Омічний контакт. Теоретичні і експериментальні залежності питомого
- 29. Найбільш важливою характеристикою контакту є питомий опір
- 30. Дякую за увагу!
Ідеальна модель і поверхневі стани Зонні енергетичні діаграми контактів метал-напівпровідник q m - q ( + Vn). Контактна різниця потенціалів. qBn = q (m - ).
Слайд 1ОСНОВИ МІКРО- і НАНОЕЛЕКТРОНІКИ
Лекція 03
Контакт метал - напівпровідник
Анатолій Євтух
Інститут
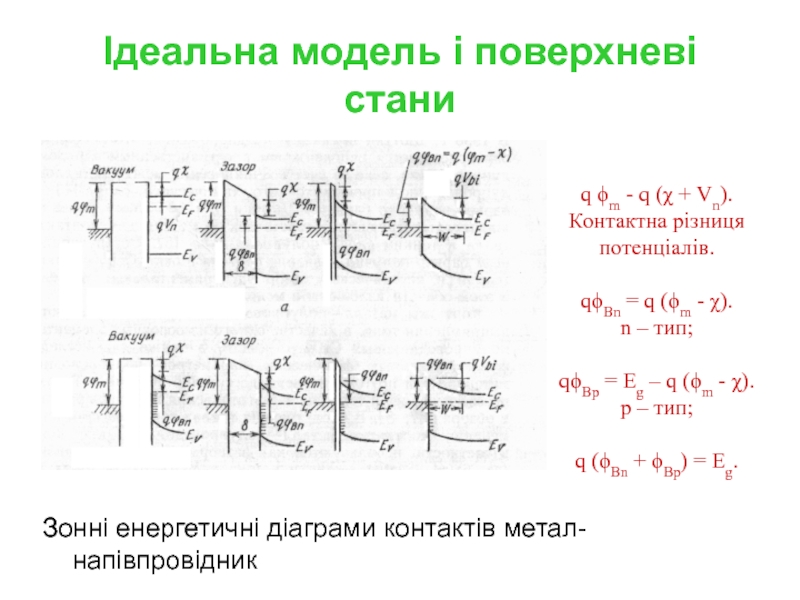
Слайд 2Ідеальна модель і поверхневі стани
Зонні енергетичні діаграми контактів метал-напівпровідник
q m -
q ( + Vn).
Контактна різниця потенціалів.
qBn = q (m - ). n – тип;
qBp = Eg – q (m - ). p – тип;
q (Bn + Bp) = Eg.
Контактна різниця потенціалів.
qBn = q (m - ). n – тип;
qBp = Eg – q (m - ). p – тип;
q (Bn + Bp) = Eg.
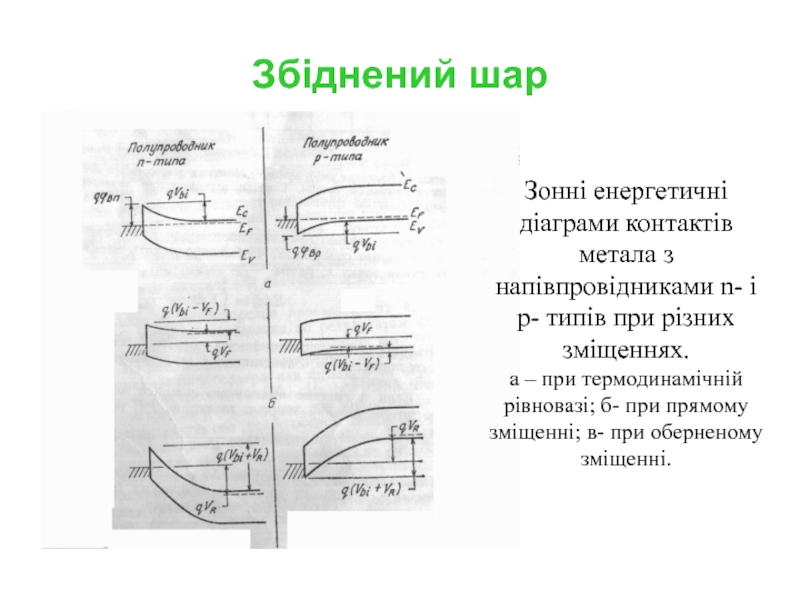
Слайд 3Збіднений шар
Зонні енергетичні діаграми контактів метала з напівпровідниками n- і p-
типів при різних зміщеннях.
а – при термодинамічній рівновазі; б- при прямому зміщенні; в- при оберненому зміщенні.
а – при термодинамічній рівновазі; б- при прямому зміщенні; в- при оберненому зміщенні.
Слайд 4Рівняння Пуасона: 2=-/0s
Різкий несиметричний p-n перехід;
Наближення різкої границі збідненого шару:
(qND при
xW )
W- ширина збідненого шару.
W- ширина збідненого шару.
Слайд 5Питома ємність збідненого шару
Якщо концентрація ND постійна у всій області збідненого
шару, то на графіку 1/C2 від V отримаємо пряму лінію.
Якщо концентрація ND не постійна, то, вимірюючи диференційну ємність можна визначити профіль легування.
Якщо концентрація ND не постійна, то, вимірюючи диференційну ємність можна визначити профіль легування.
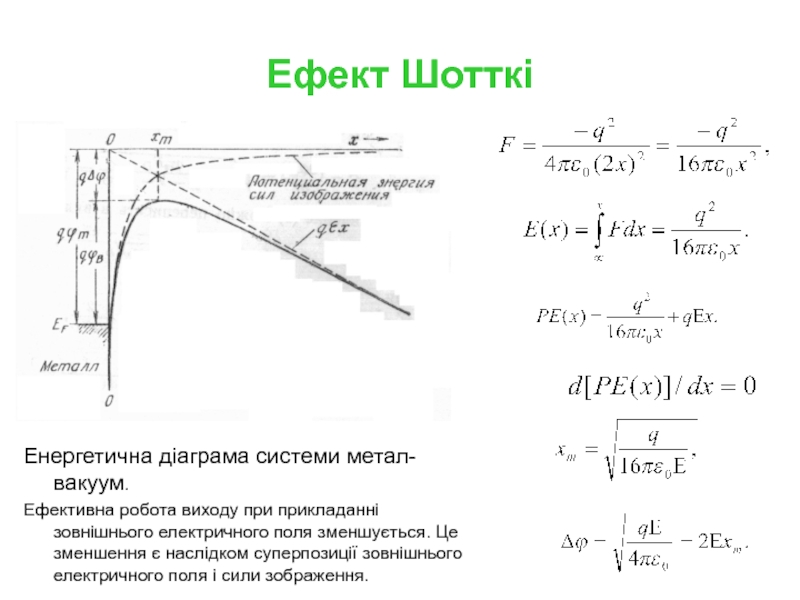
Слайд 6Ефект Шотткі
Енергетична діаграма системи метал-вакуум.
Ефективна робота виходу при прикладанні зовнішнього електричного
поля зменшується. Це зменшення є наслідком суперпозиції зовнішнього електричного поля і сили зображення.
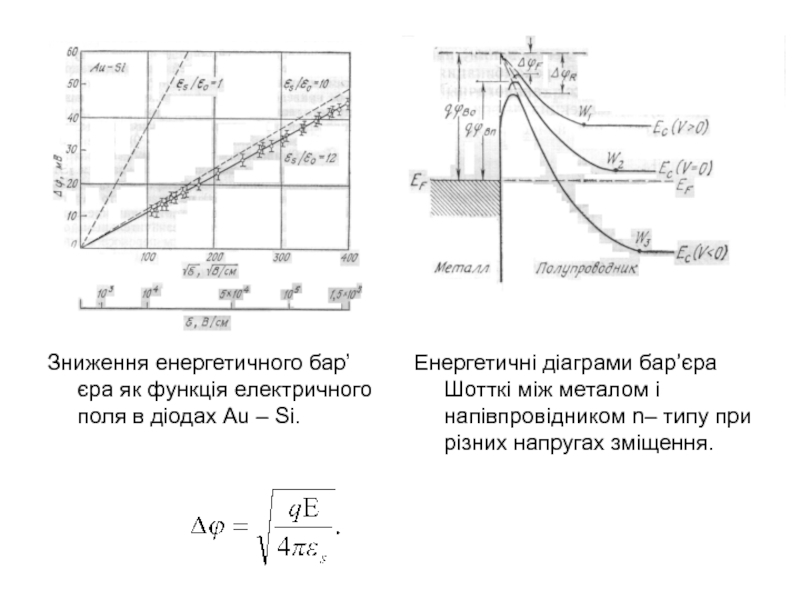
Слайд 7Зниження енергетичного бар’єра як функція електричного поля в діодах Au –
Si.
Енергетичні діаграми бар’єра Шотткі між металом і напівпровідником n– типу при різних напругах зміщення.
Слайд 8Теорія процесів переносу заряда
Чотири основні процеси переносу при прямому зміщенні.
1.Надбар’єрний переніс.
2. Квантовомеханічне тунелювання електронів через бар’єр.
3. Рекомбінація в області просторового заряду.
4. Інжекція дірок із металу в напівпровідник.
Слайд 91. Теорія термоелектронної емісії.
Припущення:
1. Висота бар’єру qBn набагато більша kT
2. Область,
що визначає термоелектронну емісію, знаходиться в термодинамічній рівновазі.
3. Протікання повного струму не порушує цієї рівноваги.
3. Протікання повного струму не порушує цієї рівноваги.
Струм не залежить від форми бар’єра, а лише від його висоти.
Слайд 102. Дифузійна теорія
Припущення:
1. Висота бар’єру qBn набагато більша kT шарі грає
суттєву роль.
3. Концентрація носіїв при x=0 і x=W не залежить від
2. Розсіяння електронів при їх русі в збідненому струму.
4. Концентрація домішок в напівпровіднику досить мала, і виродження відсутнє.
Необхідно враховувати дві компоненти струму (дифузійну та польову):
3. Концентрація носіїв при x=0 і x=W не залежить від
2. Розсіяння електронів при їх русі в збідненому струму.
4. Концентрація домішок в напівпровіднику досить мала, і виродження відсутнє.
Необхідно враховувати дві компоненти струму (дифузійну та польову):
Співвідношення Ейнштейна:
Співвідношення Ейнштейна:
Граничні умови:
Граничні умови:
Слайд 11Розподіл потенціалу в бар’єрі Шотткі:
JSD сильніше залежить від напруги і менш
чутлива до температури, ніж JST.
Слайд 123. Термоемісійна- дифузійна теорія.
Енергетична діаграма контакту з урахуванням ефекту Шотткі. q(x)–
потенціальна енергія електрона, q(x) - положення квазірівня Фермі.
В якості граничної умови використовується швидкість термоелектронної рекомбінації vR на границі розділу метал-напівпровідник.
n- густина електронів в точці х
Між xm і x=0
.
де
-ефективна швидкість дифузії.
Слайд 13Якщо vD>>vR, то передекспоненційному члені залишається лише vR і справедлива теорія
термоелектронної емісії.
Якщо vD<
Остаточний вираз для вольт-амперної характеристики:
Якщо vD<
Остаточний вираз для вольт-амперної характеристики:
де
ймовірність проходження електроном бар’єра з урахуванням розсіювання на оптичних фононах.
fQ- відношення повного струму до струму при нехтуванні квантовомеханічним тунелюванням і відбиванням.
Слайд 14Ефективна постійна Річардсона
Розрахункові значення ефективної постійної Річардсона як функціії електричного поля
в бар’єрі метал-кремній.
Слайд 154. Тунельний струм
Дві компоненти струму: термоелектронна і тунельна.
n- фактор неідеальності.
При V>>kT/q
Тунельна
компонента густини струму домінує при високому рівні легування і низьких температурах.
Тунельний струм експоненційно залежить від
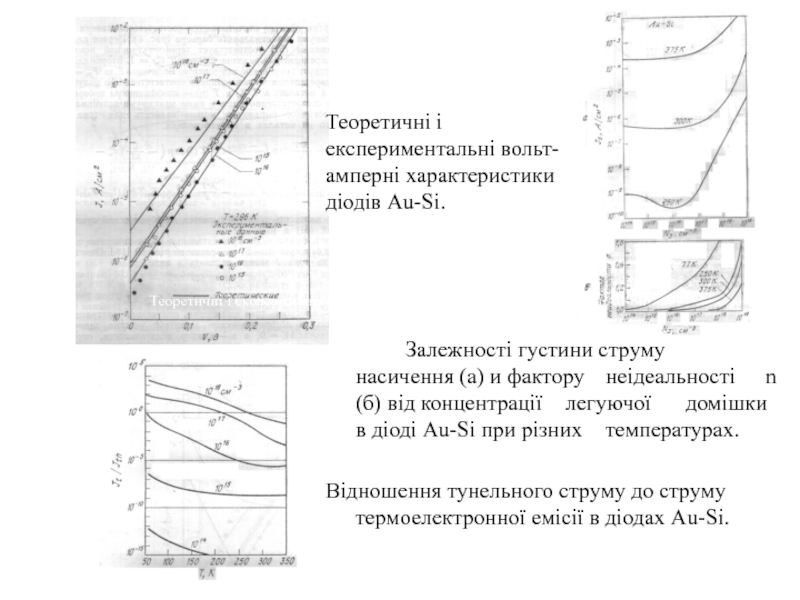
Слайд 16 Залежності густини струму насичення (а) и фактору неідеальності n (б) від
концентрації легуючої домішки в діоді Au-Si при різних температурах.
Відношення тунельного струму до струму термоелектронної емісії в діодах Au-Si.
Відношення тунельного струму до струму термоелектронної емісії в діодах Au-Si.
Теоретичні і експериментальні вольт-амперні характеристики діодів Au-Si.
Теоретичні і експериментальні вольт-амперні характеристики діодів Au-Si.
Слайд 175. Інжекція неосновних носіїв.
Енергетична діаграма епітаксійного бар’єру Шотткі.
Рівняння неперервності:
Рівняння густини струму
для неосновних носіїв:
При низькому рівні інжекції можна знехтувати дрейфовим членом в порівнянні з дифузійним. Отримуємо:
При збільшенні електричного поля домінуючою стає дрейфова компонента.
- росте пропорційно густині струму.
Слайд 18Висота бар’єра
Детальна енергетична діаграма контакту метал-напівпровідник – типу при наявності проміжного
шару товщиною порядку міжатомних відстаней.
qm- робота виходу метала; qBn- висота енергетичного барєру; qB0- асимптотичне значення при нульовому електричному полі; 0- енергетичний рівень на поверхні;
- зниження барєра за рахунок сил зображення; - падіння потенціалу на проміжному шарі; - електронна спорідненість напівпровідника; Vbi- вбудований потенціал;
s- діелектрична проникність напівпровідника; i- діелектрична проникність проміжного шару; - товщина проміжного шару; Qsc- густина обємного заряду в напівпровіднику,
Qss- густина заряду на поверхневих станах напівпровідника; Qm- густина поверхневого заряду в металі.
Слайд 19Висота бар’єра
Два припущення:
1.Товщина проміжного шару між металом і напівпровідником або дорівнює
нулю, або порядку міжатомних розмірів і тому він є тунельно прозорим для електронів , а його вплив зводиться лише до падіння потенціалу на ньому.
2. Енергетична густина поверхневих станів не залежить від типу металу і визначається лише властивостями поверхні напівпровідника.
Густина заряду на поверхневих станах:
2. Енергетична густина поверхневих станів не залежить від типу металу і визначається лише властивостями поверхні напівпровідника.
Густина заряду на поверхневих станах:
Поверхнева густина заряду збідненого шару напівпровідника:
Закон Гауса:
Виключим і отримуєм:
Слайд 20Вирішуємо відносно Bn і отримуємо:
де
При s100, i=0 і ND
c1 мала тому вираз для висоти бар’єру спрощується до виду
Якщо c1 і c3 можна визначити експериментально, а значення відомо, то
І із виразу для c2:
Слайд 21Два граничні випадки:
1. Якщо Ds , то c2
0 і
В цьому випадку рівень Фермі на поверхні фіксується поверхневими станами на енергії, що перевищує край валентної зони на величину q0 . При цьому висота бар’єра не залежить від роботи виходу металу і повністю визначається ступенем легування і поверхневими властивостями напівпровідника.
2. Якщо Ds 0 , то c2 1 і
Висота енергетичного бар’єра ідеального діода Шотткі (при відсутності поверхневих станів).
Слайд 22Виміри висоти бар’єру.
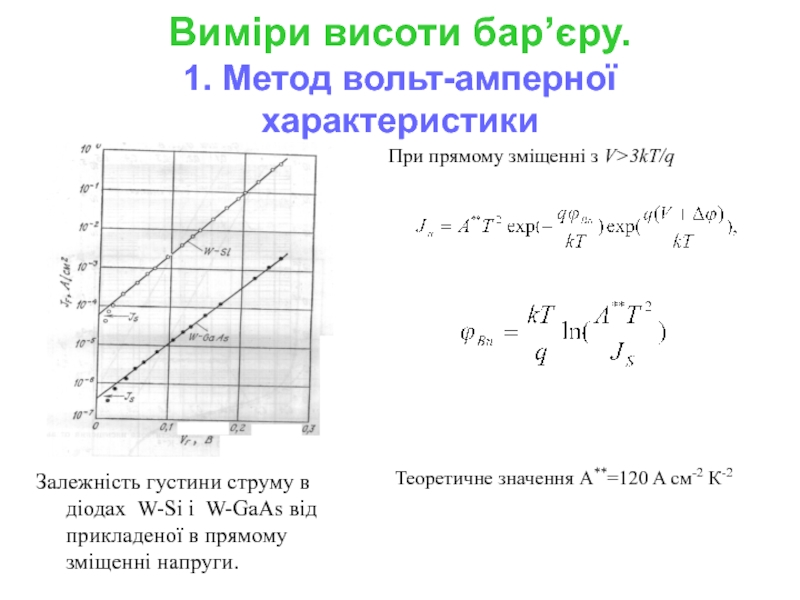
1. Метод вольт-амперної характеристики
Залежність густини струму в діодах W-Si
і W-GaAs від прикладеної в прямому зміщенні напруги.
При прямому зміщенні з V>3kT/q
Теоретичне значення A**=120 A cм-2 К-2
Слайд 232. Метод енергії активації.
Залежність струму від температури в координатах, що використовуються
для визначення висоти бар’єру.
Ае- площа електрично активної області.
При постійній напрузі прямого зміщення з тангенса кута нахилу залежності ln(IF/T2) від 1/T знайдемо висоту бар’єра Bn.
Слайд 243. Метод вольт-фарадної характеристики
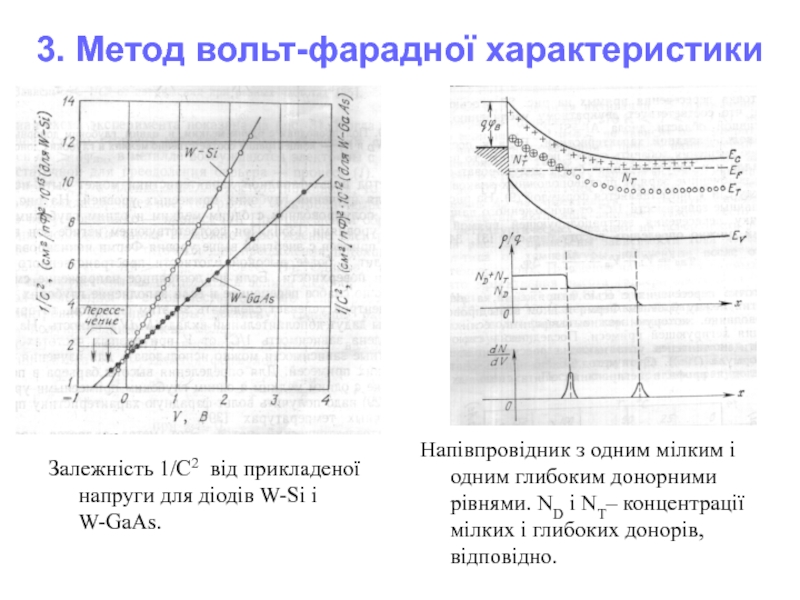
Залежність 1/C2 від прикладеної напруги для діодів W-Si
і W-GaAs.
Напівпровідник з одним мілким і одним глибоким донорними рівнями. ND і NT– концентрації мілких і глибоких донорів, відповідно.
Слайд 25Якщо концентрація ND постійна у всій області збідненого шару, то на
графіку 1/C2 від V отримаємо пряму лінію.
Якщо концентрація ND не постійна, то, вимірюючи диференційну ємність можна визначити профіль легування.
Якщо концентрація ND не постійна, то, вимірюючи диференційну ємність можна визначити профіль легування.
Висота бар’єра визначається із залежності 1/С2 від V.
де Vi - точка перетину з віссю напруг, а qVn - різниця енергій між рівнем Фермі і дном зони провідності напівпровіднику, яку можна вирахувати, якщо відома концентрація легуючої домішки. Останню можна знайти з тангенса кута нахилу залежності 1/С2 від V.
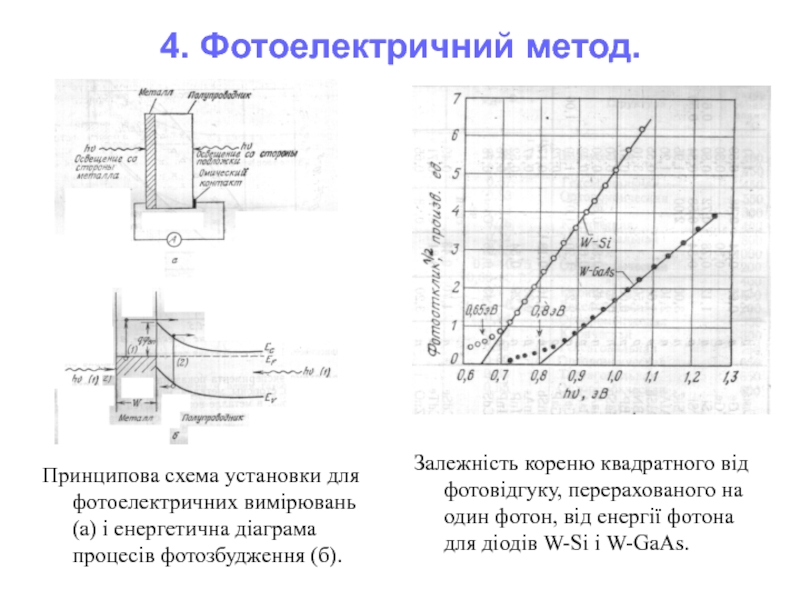
Слайд 264. Фотоелектричний метод.
Принципова схема установки для фотоелектричних вимірювань (а) і енергетична
діаграма процесів фотозбудження (б).
Залежність кореню квадратного від фотовідгуку, перерахованого на один фотон, від енергії фотона для діодів W-Si і W-GaAs.
Слайд 27Теорія Фаулера.
Залежність квантового виходу R від енергії фотона h виражається формулою:
де
h0=qBn - висота бар’єру, Es - сума h0 і енергії Фермі, відрахована від дна зони провідності металу, x=h(-0)/kT.
При умові Es>> h і x>3 отримуємо спрощений вираз
при
або
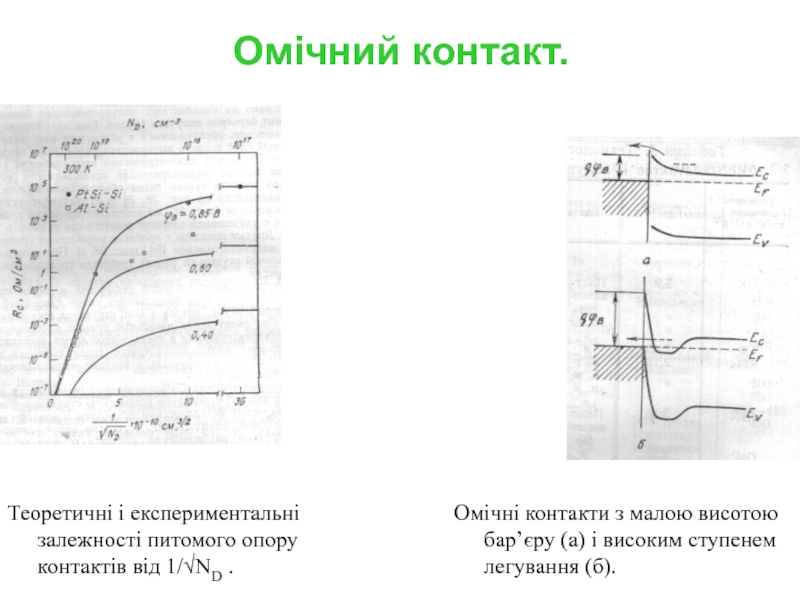
Слайд 28Омічний контакт.
Теоретичні і експериментальні залежності питомого опору контактів від 1/ND .
Омічні
контакти з малою висотою бар’єру (а) і високим ступенем легування (б).
Слайд 29Найбільш важливою характеристикою контакту є питомий опір при нульовому зміщенні
1. В
контакті метал-напівпровідник з низьким рівнем легування домінує термоелектронна компонента струму
В цьому випадку
2. В контакті метал-напівпровідник з більш високим рівнем легування домінує тунельна компонента струму
При цьому
Звідси видно, що в тунельній області питомий опір контакту експоненційно залежить від
