- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Измерения в психологии презентация
Содержание
- 1. Измерения в психологии
- 2. Обыденное и научное познание Измерение Описание Статистические
- 3. ГС и выборка Репрезентативность Случайный отбор и
- 4. Первый опыт проверки статистической достоверности Арбутнот: «Свидетельство
- 5. Гипотезы: содержательные и статистические 1. Содержательная гипотеза:
- 6. Теоретическое распределение и p-уровень значимости Пример:
- 7. Нормальное распределение IQ © Наследов А. Д, 2012
- 8. Что такое p-уровень p-уровень значимости – вероятность
- 9. Статистический критерий - z-критерий. - t-критерий Стьюдента. © Наследов А. Д, 2012
- 10. Статистическое решение 1-α 1-β p: 0 1
- 11. © Наследов А. Д, 2012
- 12. Направленные и ненаправленные альтернативы Ненаправленная альтернатива: Направленная альтернатива: © Наследов А. Д, 2012
- 13. Что такое p-уровень? Вероятность случайного получения такого
- 14. Типичные ошибки интерпретации p-уровня значимости © Наследов А. Д, 2012
- 15. 1. Содержательная интерпретация Подтверждение
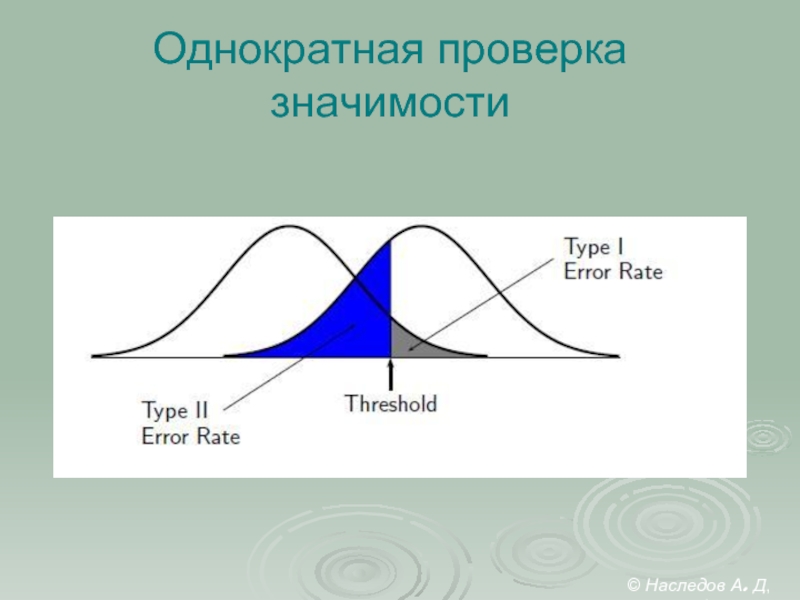
- 16. Однократная проверка значимости © Наследов А. Д, 2012
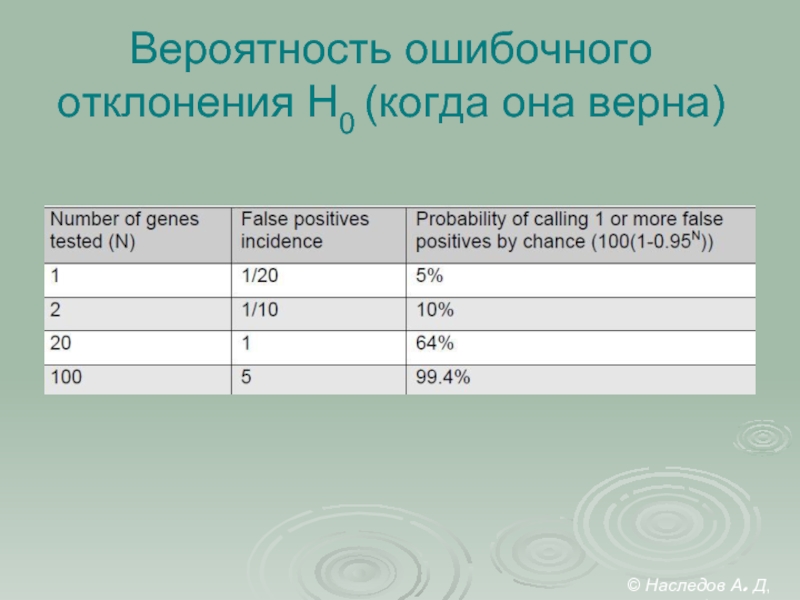
- 17. Вероятность ошибочного отклонения Н0 (когда она верна) © Наследов А. Д, 2012
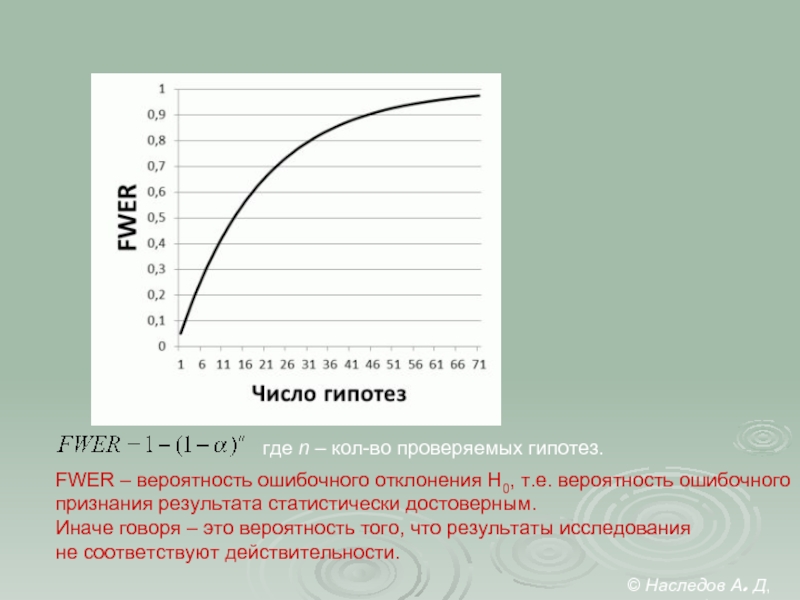
- 18. FWER – вероятность ошибочного отклонения H0,
- 19. Учет множественности статистических проверок Применение
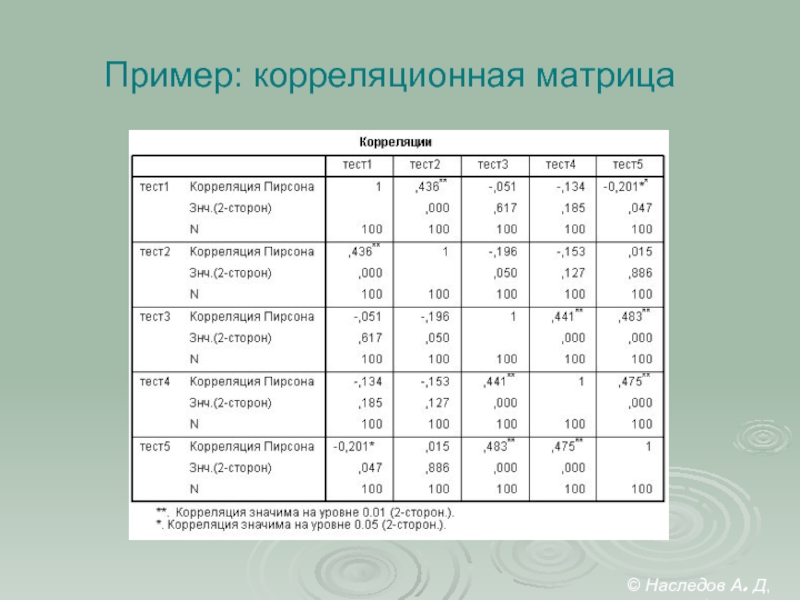
- 20. Пример: корреляционная матрица © Наследов А. Д, 2012
- 21. Последствия коррекции многократной проверки значимости При одном
- 22. Рекомендации Минимизировать кол-во измерений за счет увеличения
- 23. Модель исследования Содержательная гипотеза Измерительная модель Статистический
- 24. Измерения и шкалы Объекты (случаи) Свойства и
- 25. Измерительные шкалы Номинативная (номинальная, наименований, неколичественная). Операция
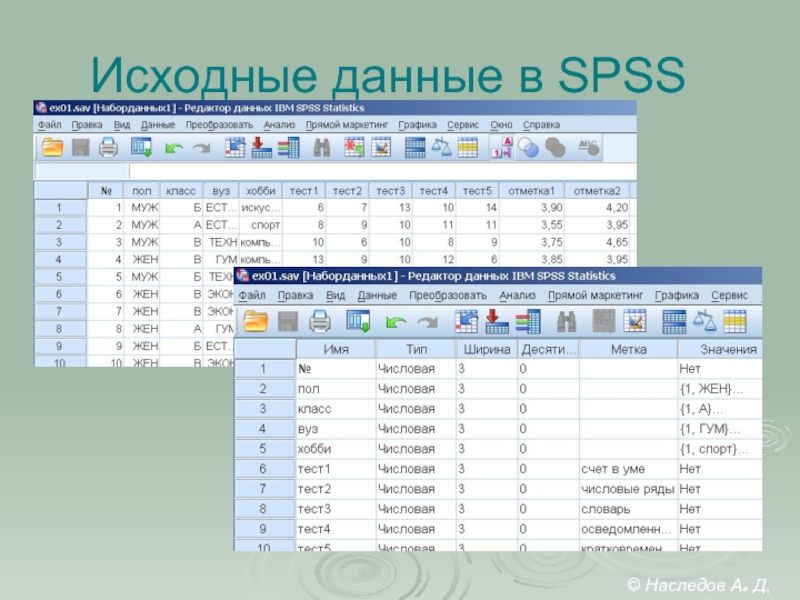
- 26. Исходные данные в SPSS © Наследов А. Д, 2012
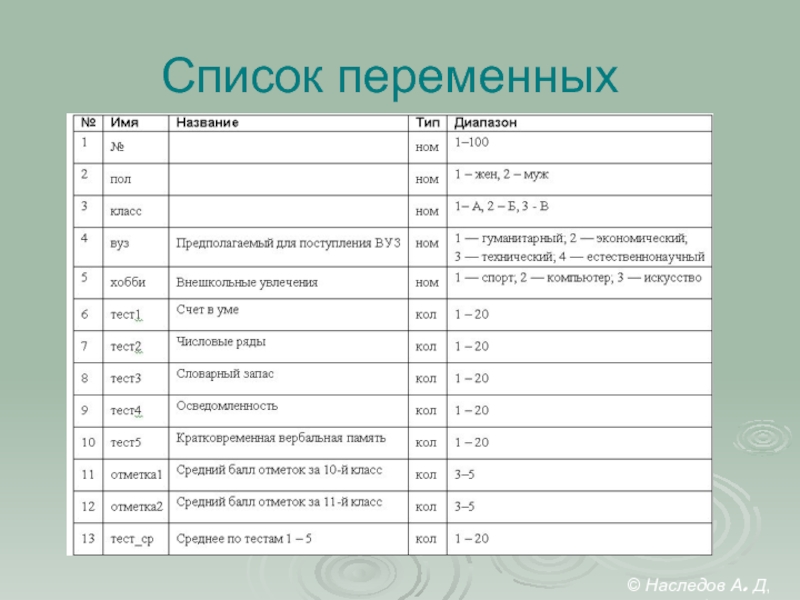
- 27. Список переменных © Наследов А. Д, 2012
- 28. Распределения частот (номинальные переменные) Таблица распределения:
- 29. Распределения частот (количественные переменные) Переменная x –
- 30. Виды графиков распределения Если Х – кол-во
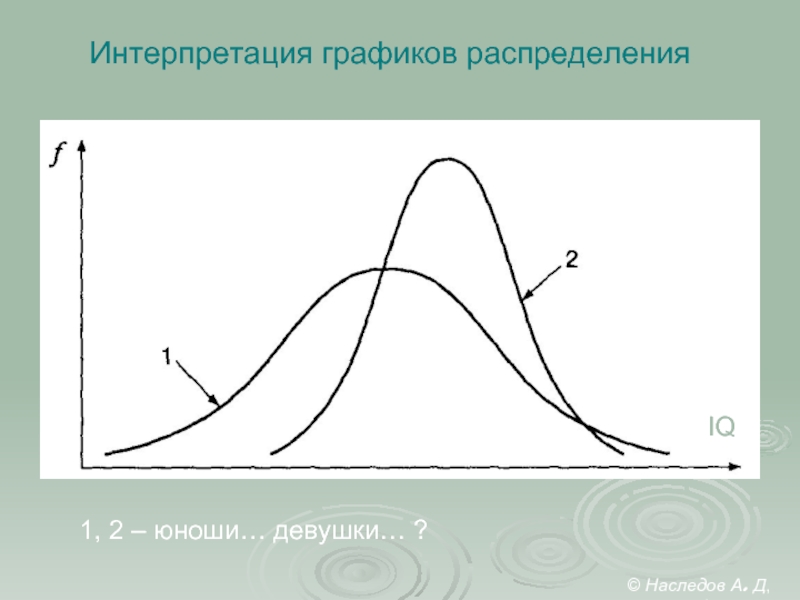
- 31. Интерпретация графиков распределения IQ 1, 2 – юноши… девушки… ? © Наследов А. Д, 2012
- 32. «Постулат нормальности»: нормальное распределение IQ ©
- 33. Проверка нормальности Зачем? Визуально, по графику распределения
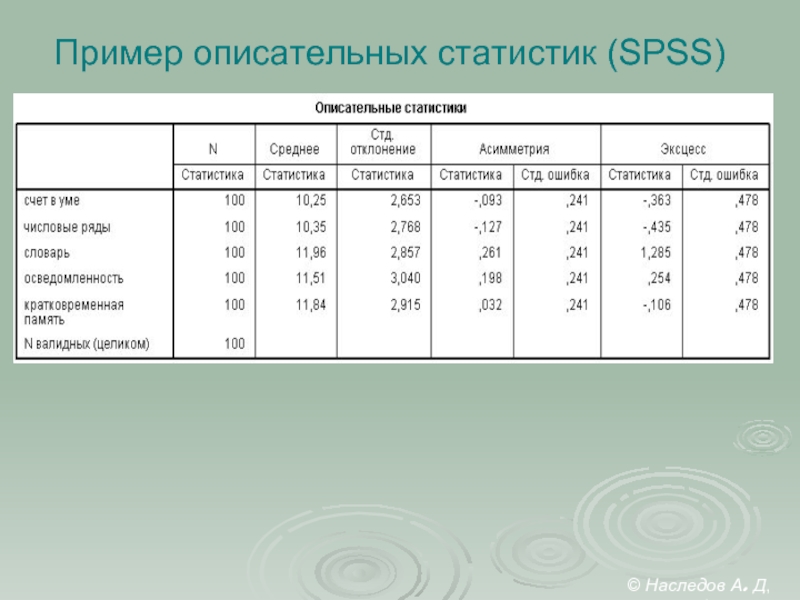
- 34. Пример описательных статистик (SPSS) © Наследов А. Д, 2012
Обыденное и научное познание Измерение Описание Статистические выводы Реальность выборка © Наследов А. Д, 2012
Слайд 1Измерения в психологии
Измерения в структуре психологического исследования
© Наследов А. Д, 2012
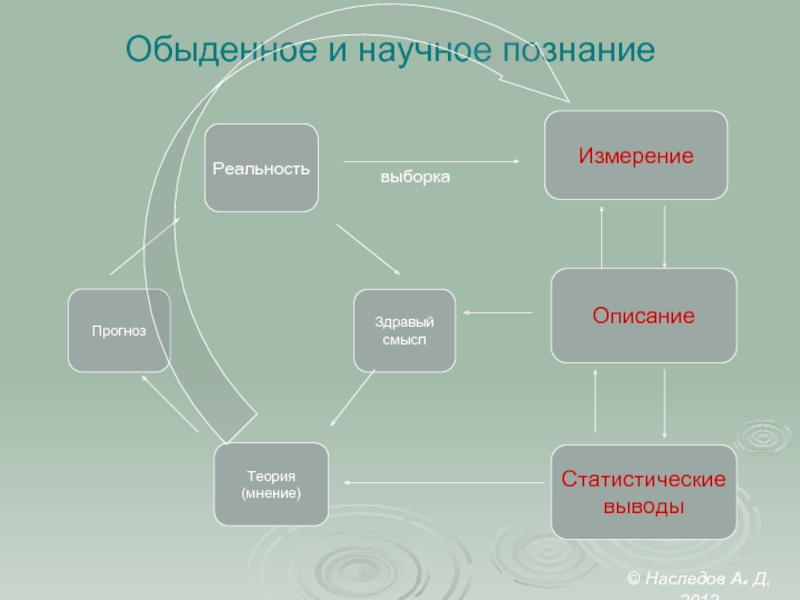
Слайд 2Обыденное и научное познание
Измерение
Описание
Статистические
выводы
Реальность
выборка
© Наследов А. Д, 2012
Слайд 3ГС и выборка
Репрезентативность
Случайный отбор и доступность
Детальное описание выборки и процедуры ее
формирования
Сравнение выборок: независимые и зависимые выборки
Сравнение выборок: независимые и зависимые выборки
© Наследов А. Д, 2012
Слайд 4Первый опыт проверки статистической достоверности
Арбутнот: «Свидетельство в пользу божественного провидения, полученное
путем систематического наблюдения за рождением обоих полов» (ХVII век)
Гипотеза: божественное провидение устанавливает иное соотношение рождаемости – в пользу мальчиков, нежели слепой рок (1/2 и 1/2).
Факты: 82 года подряд, ежегодно, мальчиков рождалось в Англии больше, чем девочек.
Логика доказательства:
Если это так, то какова вероятность того, что факт – результат случайного совпадения?
Гипотеза: божественное провидение устанавливает иное соотношение рождаемости – в пользу мальчиков, нежели слепой рок (1/2 и 1/2).
Факты: 82 года подряд, ежегодно, мальчиков рождалось в Англии больше, чем девочек.
Логика доказательства:
Если это так, то какова вероятность того, что факт – результат случайного совпадения?
p-уровень, значимость (знч.), Significant Level (sig.)
© Наследов А. Д, 2012
Слайд 5Гипотезы: содержательные и статистические
1. Содержательная гипотеза:
утверждение о связи 2-х явлений
в ГС.
2. В результате выборочного исследования:
связь в терминах описательных статистик (M1 и М2; rxy и т.п.).
3. Статистическая гипотеза: утверждение о связи параметров ГС.
– параметры.
Основная (нулевая) статистическая гипотеза (H0) –
утверждение об отсутствии связи в терминах параметров ГС.
Например:
4. Определение p-уровня значимости (знч.) и принятие статистического решения:
Н0 отклоняется (результат статистически достоверен)
Н0 не отклоняется (результат статистически не достоверен)
См. «Математические методы…», гл. 7 (стр. 93 – 110)
2. В результате выборочного исследования:
связь в терминах описательных статистик (M1 и М2; rxy и т.п.).
3. Статистическая гипотеза: утверждение о связи параметров ГС.
– параметры.
Основная (нулевая) статистическая гипотеза (H0) –
утверждение об отсутствии связи в терминах параметров ГС.
Например:
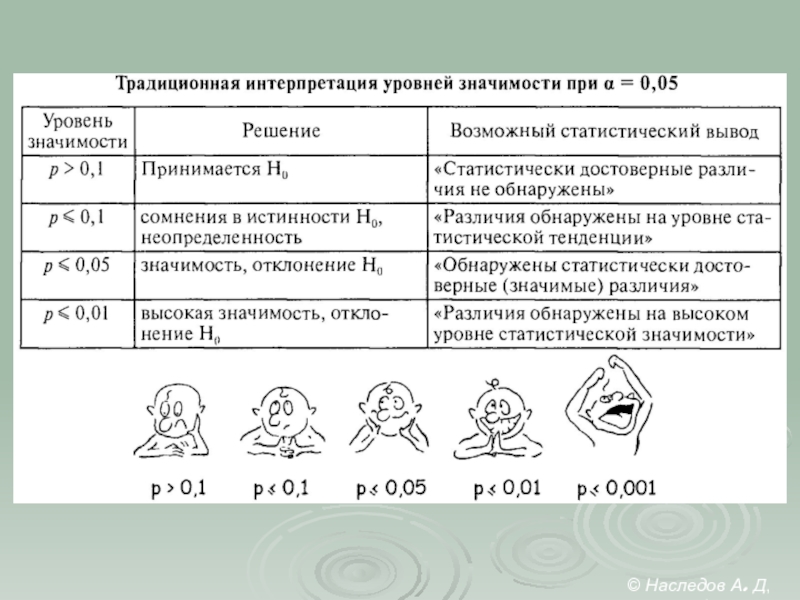
4. Определение p-уровня значимости (знч.) и принятие статистического решения:
Н0 отклоняется (результат статистически достоверен)
Н0 не отклоняется (результат статистически не достоверен)
См. «Математические методы…», гл. 7 (стр. 93 – 110)
© Наследов А. Д, 2012
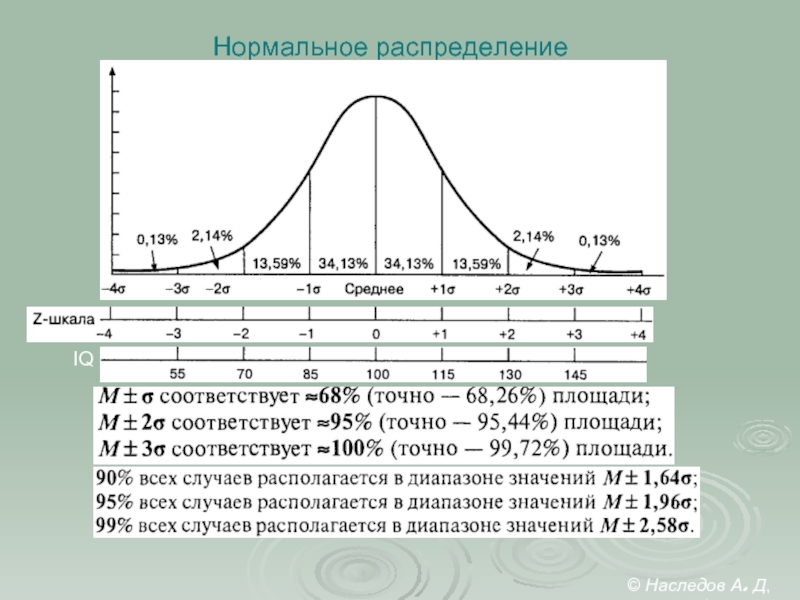
Слайд 6Теоретическое распределение
и p-уровень значимости
Пример: проверка состоятельности тестовой нормы IQ =
100.
Выборочные статистики:
Статистическая гипотеза:
Теоретическое распределение соответствует распределению статистики для выборок, многократно извлекаемых из ГС, для которой верна H0.
«Центральная предельная теорема»:
распределение выборочных средних из ГС при достаточно большом N является нормальным.
Для распределения выборочных средних:
Выборочные статистики:
Статистическая гипотеза:
Теоретическое распределение соответствует распределению статистики для выборок, многократно извлекаемых из ГС, для которой верна H0.
«Центральная предельная теорема»:
распределение выборочных средних из ГС при достаточно большом N является нормальным.
Для распределения выборочных средних:
© Наследов А. Д, 2012
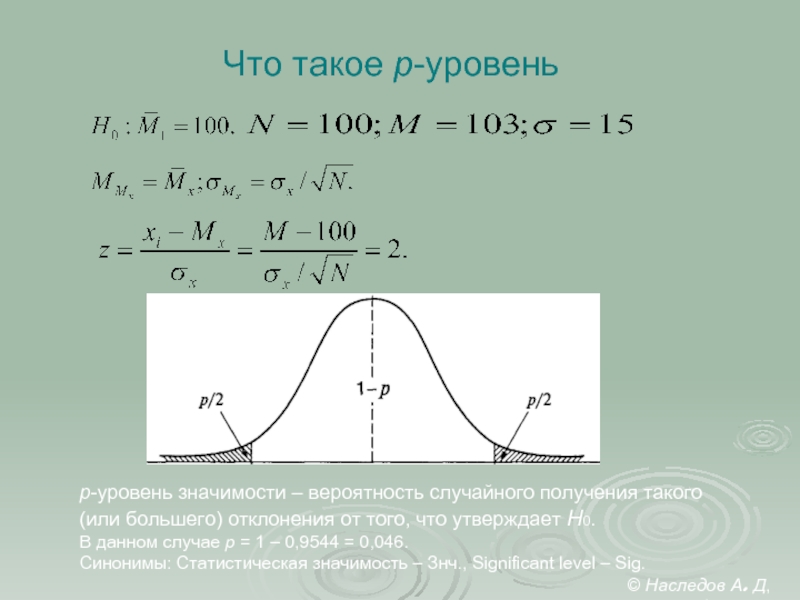
Слайд 8Что такое p-уровень
p-уровень значимости – вероятность случайного получения такого
(или большего)
отклонения от того, что утверждает H0.
В данном случае p = 1 – 0,9544 = 0,046.
Синонимы: Статистическая значимость – Знч., Significant level – Sig.
В данном случае p = 1 – 0,9544 = 0,046.
Синонимы: Статистическая значимость – Знч., Significant level – Sig.
© Наследов А. Д, 2012
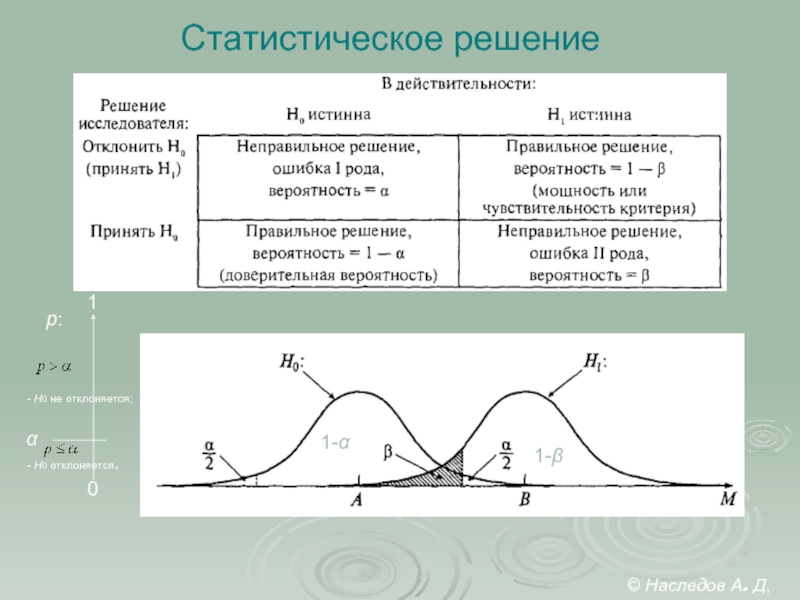
Слайд 10Статистическое решение
1-α
1-β
p:
0
1
α
- H0 не отклоняется;
- Н0 отклоняется.
© Наследов А. Д,
2012
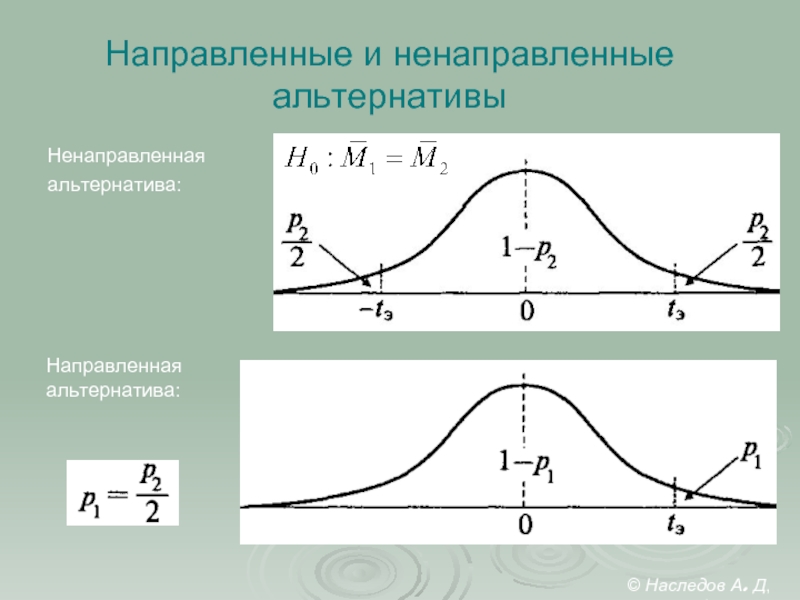
Слайд 12Направленные и ненаправленные альтернативы
Ненаправленная
альтернатива:
Направленная
альтернатива:
© Наследов А. Д, 2012
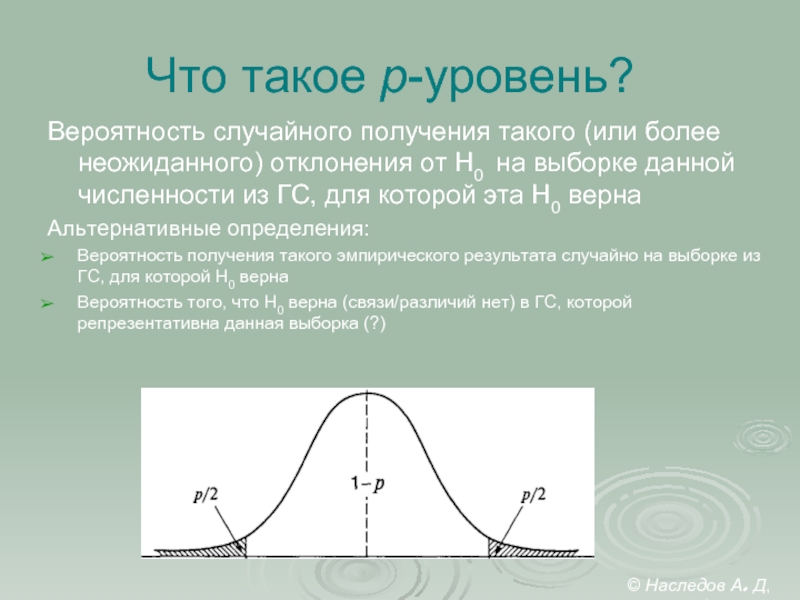
Слайд 13Что такое p-уровень?
Вероятность случайного получения такого (или более неожиданного) отклонения от
Н0 на выборке данной численности из ГС, для которой эта Н0 верна
Альтернативные определения:
Вероятность получения такого эмпирического результата случайно на выборке из ГС, для которой Н0 верна
Вероятность того, что Н0 верна (связи/различий нет) в ГС, которой репрезентативна данная выборка (?)
Альтернативные определения:
Вероятность получения такого эмпирического результата случайно на выборке из ГС, для которой Н0 верна
Вероятность того, что Н0 верна (связи/различий нет) в ГС, которой репрезентативна данная выборка (?)
© Наследов А. Д, 2012
Слайд 15
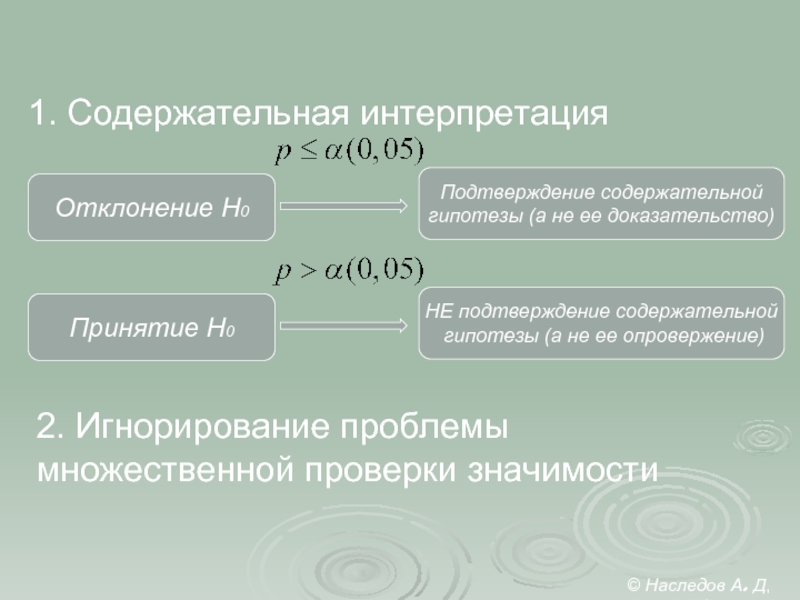
1. Содержательная интерпретация
Подтверждение содержательной
гипотезы (а не ее доказательство)
Отклонение H0
Принятие H0
НЕ
подтверждение содержательной
гипотезы (а не ее опровержение)
гипотезы (а не ее опровержение)
2. Игнорирование проблемы
множественной проверки значимости
© Наследов А. Д, 2012
Слайд 18
FWER – вероятность ошибочного отклонения H0, т.е. вероятность ошибочного
признания результата статистически
достоверным.
Иначе говоря – это вероятность того, что результаты исследования
не соответствуют действительности.
Иначе говоря – это вероятность того, что результаты исследования
не соответствуют действительности.
где n – кол-во проверяемых гипотез.
© Наследов А. Д, 2012
Слайд 19
Учет множественности статистических проверок
Применение многомерных методов
Поправка Бонферрони для семейства n гипотез:
для n гипотез каждый p-уровень умножаем на n, перед сравнением с α
Поправка Benjamini & Hochberg (1995; 2000) для семейства n гипотез:
Упорядочиваем все p от min до max (i – текущий номер p в ряду);
Для каждого i вычисляем: p*n/i = pкорр.;
Если pкорр.≤ α – результат статистически достоверен!
Поправка Benjamini & Hochberg (1995; 2000) для семейства n гипотез:
Упорядочиваем все p от min до max (i – текущий номер p в ряду);
Для каждого i вычисляем: p*n/i = pкорр.;
Если pкорр.≤ α – результат статистически достоверен!
© Наследов А. Д, 2012
Слайд 21Последствия коррекции многократной проверки значимости
При одном и том же пороге принятия/отклонения
Н0 (α – серая штриховка) вероятность того, что верна альтернативная гипотеза (β – синяя штриховка), может быть любой.
Поправка на многократность проверки непредсказуемо
увеличивает вероятность β.
© Наследов А. Д, 2012
Слайд 22Рекомендации
Минимизировать кол-во измерений за счет увеличения их надежности и валидности
Применять многомерные
методы для большого кол-ва измерений
Обязательно применять коррекцию p-уровня значимости при многократной проверке
Обязательно применять коррекцию p-уровня значимости при многократной проверке
© Наследов А. Д, 2012
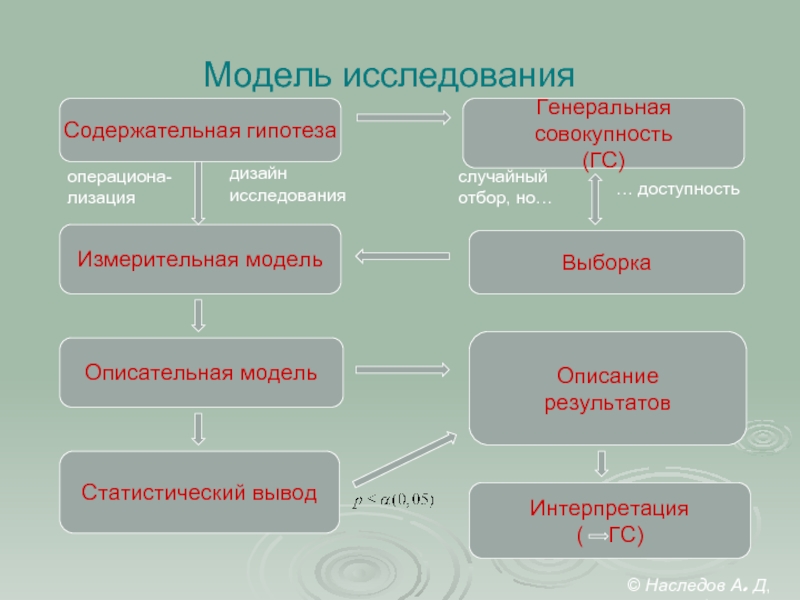
Слайд 23Модель исследования
Содержательная гипотеза
Измерительная модель
Статистический вывод
Генеральная совокупность
(ГС)
Выборка
Интерпретация
( ГС)
Описательная модель
случайный
отбор, но…
… доступность
операциона-
лизация
Описание
результатов
дизайн
исследования
© Наследов А. Д, 2012
Слайд 24Измерения и шкалы
Объекты (случаи)
Свойства и их признаки
Переменные – результаты измерений
Измерения в
психологии - косвенные
Шкала измерения (С.Стивенс): соотношение между свойствами чисел и измеряемым свойством; задается измерительной операцией.
Шкала измерения (С.Стивенс): соотношение между свойствами чисел и измеряемым свойством; задается измерительной операцией.
© Наследов А. Д, 2012
Слайд 25Измерительные шкалы
Номинативная (номинальная, наименований, неколичественная). Операция – классификация. Пол, хобби, должность…
Порядковая
(ранговая) – количественная, неметрическая. Операция – упорядочивание («больше – меньше»). Место в турнире…
Интервальная (метрическая). Равным разностям между числами соответствуют равные разности в измеряемом свойстве (единицы измерения, «равноинтервальность»). Температура по С, летоисчисление от р.х. …
Абсолютная (метрическая). «Равноинтервальная» + ноль (отсутствие измеряемого свойства). Вес, длина, время…
Интервальная (метрическая). Равным разностям между числами соответствуют равные разности в измеряемом свойстве (единицы измерения, «равноинтервальность»). Температура по С, летоисчисление от р.х. …
Абсолютная (метрическая). «Равноинтервальная» + ноль (отсутствие измеряемого свойства). Вес, длина, время…
© Наследов А. Д, 2012
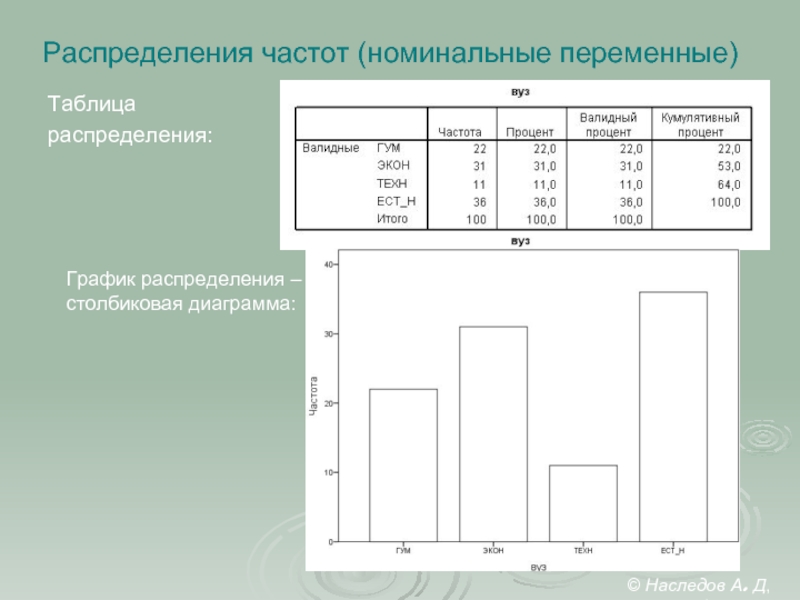
Слайд 28Распределения частот (номинальные переменные)
Таблица
распределения:
График распределения –
столбиковая диаграмма:
© Наследов А.
Д, 2012
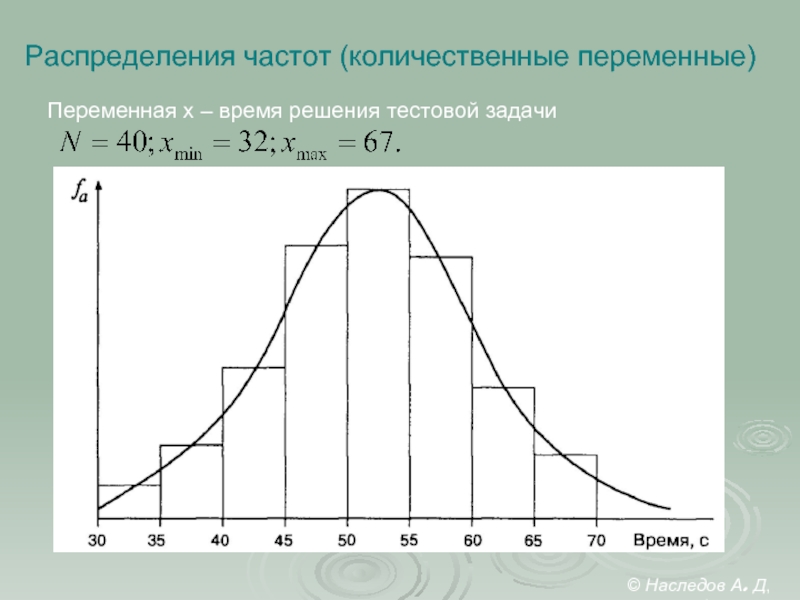
Слайд 29Распределения частот (количественные переменные)
Переменная x – время решения тестовой задачи
© Наследов
А. Д, 2012
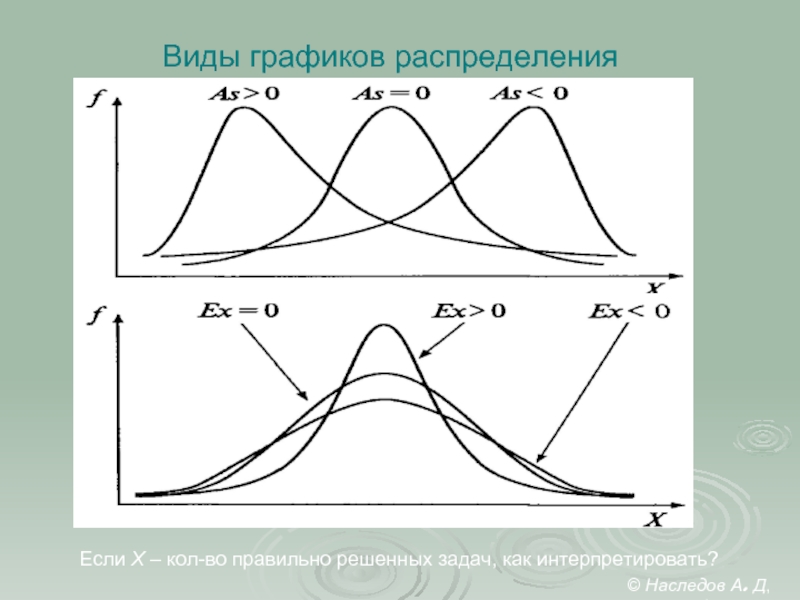
Слайд 30Виды графиков распределения
Если Х – кол-во правильно решенных задач, как интерпретировать?
©
Наследов А. Д, 2012
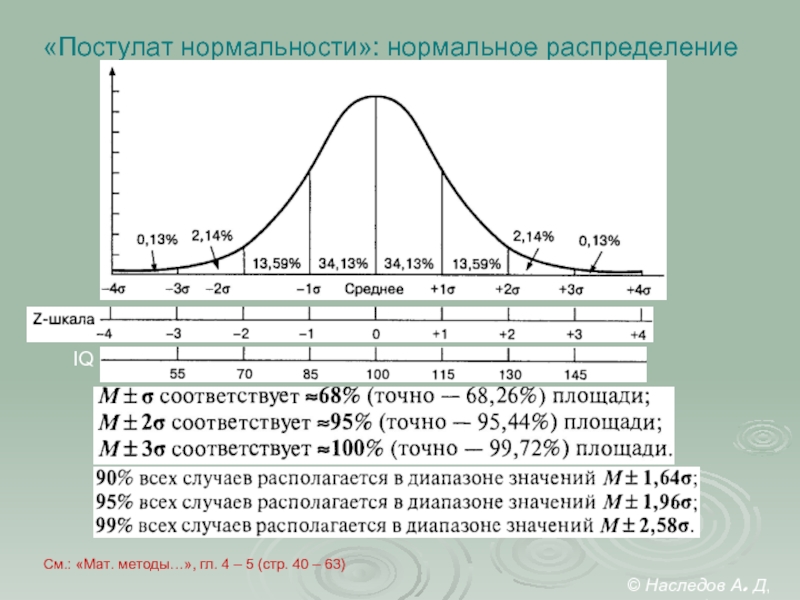
Слайд 32«Постулат нормальности»: нормальное распределение
IQ
© Наследов А. Д, 2012
См.: «Мат. методы…»,
гл. 4 – 5 (стр. 40 – 63)
Слайд 33Проверка нормальности
Зачем?
Визуально, по графику распределения и с контролем выбросов.
По критериям асимметрии
и эксцесса.
По статистическим критериям нормальности: а) К-С и К-С с поправкой Лилиефорса; б) Шапиро-Уилка
По статистическим критериям нормальности: а) К-С и К-С с поправкой Лилиефорса; б) Шапиро-Уилка
© Наследов А. Д, 2012
