- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
История развития вычислительной техники презентация
Содержание
- 1. История развития вычислительной техники
- 2. Этапы развития вычислительной техники Ручной (30 тыс.
- 3. Ручной этап 30 т.лет до н. эры – XVII век
- 4. Первые инструменты счёта 30 тыс. лет
- 5. Первые инструменты счёта
- 6. Абак Абак — первое счётное приспособление, которое
- 7. Абак Скорее всего, сначала роль абака (полагают,
- 8. Абак Древнегреческий историк Геродот (484 до н.э.—
- 9. Саламинская плита О том, что изначально данное
- 10. Саламинская доска
- 11. Римский абак Хотя в Древнем Риме абак
- 12. Римский абак Изготавливали его римляне из
- 13. Римский абак
- 14. Счёт в Китае С IV в. до
- 15. Возрождение абака Только в X в.,
- 16. Абак Герберта Абак Герберта содержал 27 колонок,
- 17. Важность абака Герберта Даже спустя шесть
- 18. Счёт на линиях В XII—XIII вв. абак
- 19. Счёт в России В России с древних
- 20. Дощаной счёт Долгое время считалось, что русские
- 21. Используя счёты найдите значение 2563 + 6745
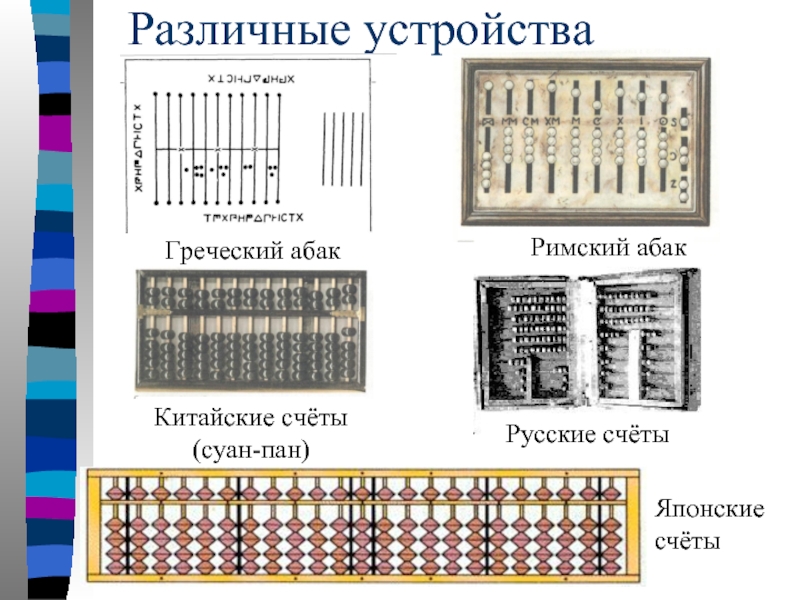
- 22. Различные устройства
- 23. Создание логарифмов Шотландский математик Джон Непер изобрёл
- 24. Палочки Непера (1617 год) Непер предложил
- 25. Палочки Непера
- 26. Перемножьте с помощью палочек Непера следующие числа
- 27. Механический этап Середина XVII века – конец XIX века
- 28. Блез Паскаль (1623 – 1662) В
- 29. Счётная машина Паскаля Главная идея конструкции
- 30. Производство машин Паскаля Паскаль показывал
- 31. Механический сумматор осуществлял сложение чисел на
- 32. Механический сумматор мог только складывать,
- 33. Англичане Роберт Биссакар, а в 1657 году
- 34. Вычислите с помощью логарифмической линейки 32 52
- 35. Вычислите с помощью логарифмической линейки 2*6 7*9 16*29 = 12 = 63 = 464
- 36. Готфрид Вильгельм Лейбниц (1646 – 1716) О
- 37. Деятельность Лейбница Сначала он хотел лишь
- 38. Лейбниц гордился своим изобретением. Вот что он
- 39. Помощь России По просьбе Петра I учёный
- 40. Заслуги Лейбница Заслуга Готфрида Вильгельма Лейбница
- 41. Чарлз Бэббидж (1792-1871) «Я отдаю
- 42. Создание разностной машины В 1822 г. Бэббидж
- 43. Аналитическая машина В 1834 г. у него
- 44. Схема работы аналитических машин Устройства
- 45. Перфокарты в машине Операционные—для выполнения
- 46. Соратница Бэббиджа Ада Августа Лавлейс предложила назвать
- 47. Задумка аналитической машины Возможности такой
- 48. Аналитическая машина Бэббиджа В аналитической машине
- 49. Создание арифмометра (1880) Вильгодт Теофилович
- 50. Вычислите с помощью арифмометра 57962+1643 65975+365 123456+99996
- 51. Электромеханический этап Конец XIX века – середина XX века
- 52. Герман Холлерит 29 февраля I860 г. в
- 53. Табулятор Холлерита для переписи населения Первый табулятор
- 54. Табулятор Холлерита Обработка результатов перепеси населеня, занесённых
- 55. Применение табулятора В 1896 г. Холлерит
- 56. Состав машины Холлерита Машину для сортировки,
- 60. Продолжение следует…
- 61. Список использованных источников http://museum.iu4.bmstu.ru/firststeps/letters.shtml - музей информатики
- 62. Список использованной литературы Энциклопедия для детей. Т.11.
Этапы развития вычислительной техники Ручной (30 тыс. лет до н.э. – середина Ручной (30 тыс. лет до н.э. – середина XVIIРучной (30 тыс. лет до н.э. – середина XVII века) Механический
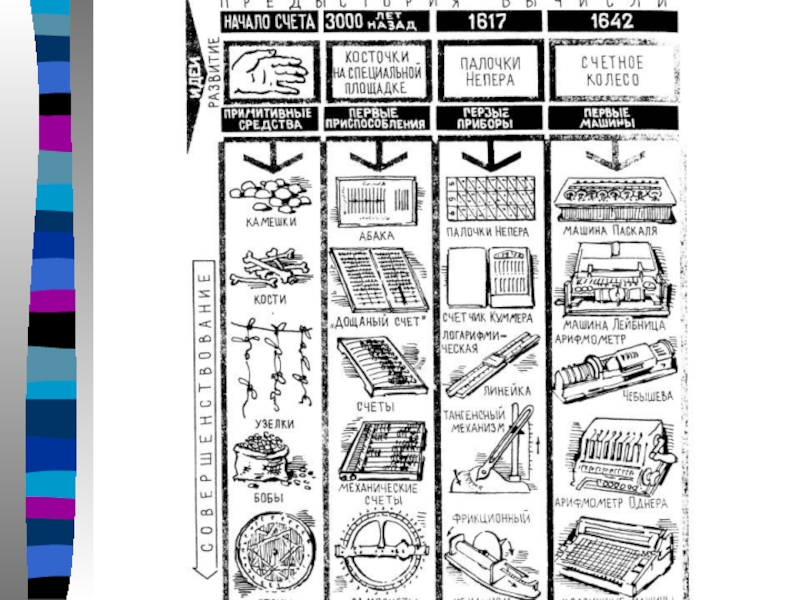
Слайд 2Этапы развития вычислительной техники
Ручной (30 тыс. лет до н.э. – середина
Ручной (30 тыс. лет до н.э. – середина XVIIРучной (30 тыс. лет до н.э. – середина XVII века)
Механический (середина Механический (середина XVIIМеханический (середина XVII века –
90-е годы 90-е годы XIX 90-е годы XIX века)
Электромеханический (90-е годы Электромеханический (90-е годы XIX Электромеханический (90-е годы XIX века – середина Электромеханический (90-е годы XIX века – середина XXЭлектромеханический (90-е годы XIX века – середина XX века)
Электронный (середина ХХ века – сегодняшние дни)
Механический (середина Механический (середина XVIIМеханический (середина XVII века –
90-е годы 90-е годы XIX 90-е годы XIX века)
Электромеханический (90-е годы Электромеханический (90-е годы XIX Электромеханический (90-е годы XIX века – середина Электромеханический (90-е годы XIX века – середина XXЭлектромеханический (90-е годы XIX века – середина XX века)
Электронный (середина ХХ века – сегодняшние дни)
Слайд 4Первые инструменты счёта
30 тыс. лет до н.э.
В 1937 г. в
Вестонице (Моравия) на месте одной из стоянок найдена волчья кость с 55 глубокими зарубками (один знак), которую назвали
«вестоницкая кость».
Позволяет историкам предположить, что уже тогда наши предки были знакомы с зачатками счета.
«вестоницкая кость».
Позволяет историкам предположить, что уже тогда наши предки были знакомы с зачатками счета.
Слайд 6Абак
Абак — первое счётное приспособление, которое
стал применять человек.
Идея его
устройства заключается в наличии специального вычислительного поля, где по определённым правилам перемещают счётные элементы, сгруппированные по разрядам. Именно эта идея объединяет столь разные на первый взгляд приборы, как греческий и римский абак, китайские и русские счёты, а также счёт на линиях.
Слайд 7Абак
Скорее всего, сначала роль абака (полагают, что корень этого греческого
слова
означает «пыль») выполняла покрытая пылью или песком доска, на которой можно было чертить линии и перекладывать камешки. Абак был известен ещё в Древнем Египте и, возможно, в Вавилонии, а финикийские купцы завезли его в Грецию.
Слайд 8Абак
Древнегреческий историк Геродот (484 до н.э.— около 425 до н. э.)
свидетельствует, что «эллины пишут свои буквы и считают слева направо, а египтяне — справа налево».
Это первое письменное упоминание об абаке. Самое раннее изображение абака можно увидеть на вазе, изготовленной греческими мастерами в III в. до н. э. На ней рядом с персидским царём Дарием I находится казначей, занятый подсчётами на абаке.
Это первое письменное упоминание об абаке. Самое раннее изображение абака можно увидеть на вазе, изготовленной греческими мастерами в III в. до н. э. На ней рядом с персидским царём Дарием I находится казначей, занятый подсчётами на абаке.
Слайд 9Саламинская плита
О том, что изначально данное устройство служило именно для выполнения
денежных расчётов, свидетельствует и единственный сохранившийся до наших дней древнегреческий абак — так называемая саламинская плита (по имени острова Саламин в Эгейском море), найденная при раскопках в 1846 г.
Это действительно большая (размером 105 х 75 см) мраморная плита, на которой прорезаны параллельные линии, образующие несколько колонок. В левой колонке подсчитывали крупные денежные единицы — драхмы и таланты.
Это действительно большая (размером 105 х 75 см) мраморная плита, на которой прорезаны параллельные линии, образующие несколько колонок. В левой колонке подсчитывали крупные денежные единицы — драхмы и таланты.
Слайд 11Римский абак
Хотя в Древнем Риме абак и
называли
calculi — «камешки»
отсюда произошел латинский глагол calculate — «вычислять»,
а от него — русское слово «калькулятор», камешки уже не использовали.
Абак изменился, превратившись в настоящий счётный прибор.
Слайд 12Римский абак
Изготавливали его римляне из
бронзы, цветного стекла или
слоновой кости
в виде доски с двумя рядами прорезей, по которым передвигались косточки (в нижнем ряду по четыре, а в верхнем — по одной). Косточка верхнего ряда «стоила» в пять раз больше, чем расположенные под ней (например, число 80 представлялось одной косточкой верхнего и тремя косточками нижнего ряда колонки десятков: 50 + 3*10). Несколько рядов прорезей служили для представления дробей, кратных 1/12, 1/24, 1/48 и 1/72. В работе римский абак был значительно удобнее греческого.
Слайд 14Счёт в Китае
С IV в. до н. э.
абак известен в
Китае — в то время использовались счётные палочки, которые выкладывали на специальной доске. Постепенно их сменили разноцветные фишки, доска приобрела иную форму, а в X в. появились китайские счёты — суан-пан. В них место доски заняла рама с нанизанными на прутья косточками (по семь на каждом). Из Китая суан-пан в XVI в. пришёл в Японию — здесь он получил название «соробан». Рама соробана тоже состоит из двух частей, но они содержат по одной и по четыре косточки.
Слайд 15Возрождение
абака
Только в X в., после
нескольких столетий
упадка науки и
культуры,
наступивших вслед за
падением Римской империи, абак снова распространяется в Европе. Его возрождение связано с именем одного из самых ярких и образованных людей раннего Средневековья Герберта из Орийака (940—1003), ставшего в 999 г. Папой Римским Сильвестром II.
наступивших вслед за
падением Римской империи, абак снова распространяется в Европе. Его возрождение связано с именем одного из самых ярких и образованных людей раннего Средневековья Герберта из Орийака (940—1003), ставшего в 999 г. Папой Римским Сильвестром II.
Слайд 16Абак Герберта
Абак Герберта содержал 27 колонок, объединён-ных по 3, и 3
дополни-тельные колонки для представления дробей. Вместо камешков использовались специальные жетоны с нанесёнными на них цифрами от 1 до 9.
Слайд 17Важность абака
Герберта
Даже спустя шесть столетий
изобретение Герберта оста-
валось важнейшим инстру-
ментом
для практических вычислений, не случайно Блез Паскаль писал, что использование его арифметической машины позволит отказаться от утомительных расчётов «с помощью пера и жетонов». А вот создатель другой вычислительной машины, Г. В. Лейбниц, предпочитал жетоны вычислениям на бумаге.
Слайд 18Счёт на линиях
В XII—XIII вв. абак принял форму так называемого счёта
на линиях.
В нём использовались специальные разлинованные таблицы и жетоны, которые можно было помещать как на линиях, так и между ними.
До конца XVIII в. счёт на линиях сохранял свои позиции в некоторых европейских странах и лишь затем окончательно уступил место вычислениям на бумаге.
В нём использовались специальные разлинованные таблицы и жетоны, которые можно было помещать как на линиях, так и между ними.
До конца XVIII в. счёт на линиях сохранял свои позиции в некоторых европейских странах и лишь затем окончательно уступил место вычислениям на бумаге.
Слайд 19Счёт в России
В России с древних
времён был распространён
«счёт костьми»,
близкий
европейскому счёту на
линиях. Вместо жетонов обычно применялись плодовые косточки (посетивший Россию в 1634—1636 гг. немецкий учёный и путешественник Адам Олеарий отмечал, что писцы для этой цели имеют при себе мешочки с косточками сливы).
В XVI в. возник так называемый дощаной счёт, первый вариант русских счётов (спустя 100 лет появилось и само слово «счёты»).
европейскому счёту на
линиях. Вместо жетонов обычно применялись плодовые косточки (посетивший Россию в 1634—1636 гг. немецкий учёный и путешественник Адам Олеарий отмечал, что писцы для этой цели имеют при себе мешочки с косточками сливы).
В XVI в. возник так называемый дощаной счёт, первый вариант русских счётов (спустя 100 лет появилось и само слово «счёты»).
Слайд 20Дощаной счёт
Долгое время считалось,
что русские счеты ведут свое происхождение от китайского
суан-пана, и лишь в 60-х годах XX века было доказано русское происхождение этого счетного прибора - у него, во-первых, горизонтальное расположение спиц с косточками и, во-вторых, для представления чисел использована десятичная (а не пятеричная) система счисления.
Слайд 21Используя счёты найдите значение
2563 + 6745
98526 + 126
19465 + 951
= 9308
=
98652
= 20416
Например: 24675 + 365
= 25040
Слайд 23Создание логарифмов
Шотландский математик Джон Непер
изобрёл таблицы логарифмов.
Принцип их заключается в том,
что
каждому числу соответствует специальное число– логарифм – это показатель степени, в которую нужно возвести число. Таким способом можно выразить любое число. Логарифмы очень упрощают деление и умножение. Для умножения двух чисел достаточно сложить их логарифмы. Благодаря данному свойству сложная операция умножения сводилась к простой операции сложения.
каждому числу соответствует специальное число– логарифм – это показатель степени, в которую нужно возвести число. Таким способом можно выразить любое число. Логарифмы очень упрощают деление и умножение. Для умножения двух чисел достаточно сложить их логарифмы. Благодаря данному свойству сложная операция умножения сводилась к простой операции сложения.
Слайд 24Палочки Непера
(1617 год)
Непер предложил в 1617
году способ перемножения чисел.
Инструмент, получивший название палочки (или костяшки) Непера, состоял из разделенных на сегменты стерженьков, которые можно было располагать таким образом, что при сложении чисел в прилегающих друг к другу по горизонтали сегментах получался результат умножения этих чисел.
Слайд 26Перемножьте с помощью палочек Непера
следующие числа
2048 * 4
16879 * 6
23465 *
9
653497 * 8
653497 * 8
= 8192
= 101274
= 211185
= 5227976
Например: 4657 * 7
= 32599
Слайд 28Блез Паскаль
(1623 – 1662)
В 1640 г. Этьен Паскаль (отец)
получил
назначение «интендантом
полиции, юстиции и финансов» в Руан. Эта должность подразумевала и контроль за сбором налогов по всей провинции. Считается, что мысль об арифметической машине возникла у юного Блеза из-за желания помочь отцу в сложных расчётах, которые тот производил на бумаге и на счётной доске, «с помощью пера и жетонов».
полиции, юстиции и финансов» в Руан. Эта должность подразумевала и контроль за сбором налогов по всей провинции. Считается, что мысль об арифметической машине возникла у юного Блеза из-за желания помочь отцу в сложных расчётах, которые тот производил на бумаге и на счётной доске, «с помощью пера и жетонов».
Слайд 29Счётная машина
Паскаля
Главная идея конструкции
будущей машины — автома-
тический перенос разряда.
«...Каждое
колесо... некото-
рого разряда, совершая движение на десять арифметических цифр, заставляет двигаться следующее только на одну цифру».
Первая модель была готова уже через несколько месяцев, но... не работала. Паскаль приступил к разработке второй модели, над которой трудился с перерывами до 1642 г. Именно этот год считается датой изобретения, хотя первый экземпляр машины закончили лишь спустя ещё три года.
рого разряда, совершая движение на десять арифметических цифр, заставляет двигаться следующее только на одну цифру».
Первая модель была готова уже через несколько месяцев, но... не работала. Паскаль приступил к разработке второй модели, над которой трудился с перерывами до 1642 г. Именно этот год считается датой изобретения, хотя первый экземпляр машины закончили лишь спустя ещё три года.
Слайд 30Производство
машин Паскаля
Паскаль показывал
свою машину в салонах самых знатных людей
королевства, а для всеобщего обозрения выставил её в Люксембургском дворце. Один экземпляр в 1652 г. он даже послал в подарок шведской королеве Христине. Но настоящего производства наладить так и не удалось. Всего с 1645 по 1653 г. было изготовлено около 50 арифметических машин (из них восемь сохранились до наших дней).
Слайд 31Механический сумматор
осуществлял сложение чисел
на специальных дисках-ко-
лесиках. В машине Паскаля
десятичные
цифры пятизначного
числа задавались поворотами дисков, на которых были нанесены цифровые деления. Результат читался в окошечках. Диски имели один удлинённый зуб, чтобы при сложении можно было учесть перенос единицы в следующий десятичный разряд. Диски были механически связаны через промежуточные шестерни: диски сотен, десятков и единиц вращались в одну сторону — в сторону увеличения. В первом калькуляторе Паскаля было 5 цифр, затем он увеличил их до 8.
числа задавались поворотами дисков, на которых были нанесены цифровые деления. Результат читался в окошечках. Диски имели один удлинённый зуб, чтобы при сложении можно было учесть перенос единицы в следующий десятичный разряд. Диски были механически связаны через промежуточные шестерни: диски сотен, десятков и единиц вращались в одну сторону — в сторону увеличения. В первом калькуляторе Паскаля было 5 цифр, затем он увеличил их до 8.
Слайд 32Механический сумматор мог
только складывать,
для вычитаний исполь-
зовалась техника
«вычитания через
дополнение».
Например,
4125 - 737 на пятизначной машине Паскаля,
Надо к 4125 прибавить дополнение
737 до 100 000, т.е. 100 000-737 = 99263
4125-737=3388 ⇔ 4125 + 99263= 103 388.
А так как шестого разряда в пятиразрядной машине нет, то результат не 103 388, а 3388.
Например,
4125 - 737 на пятизначной машине Паскаля,
Надо к 4125 прибавить дополнение
737 до 100 000, т.е. 100 000-737 = 99263
4125-737=3388 ⇔ 4125 + 99263= 103 388.
А так как шестого разряда в пятиразрядной машине нет, то результат не 103 388, а 3388.
Слайд 33Англичане Роберт Биссакар, а в 1657 году – независимо от него
С. Патридж разработали прямоугольную логарифмическую линейку, конструкция которой в основном сохранилась до наших дней.
Линейка Уатта - первая универсальная логарифмическая линейка, пригодная для выполнения любых инженерных расчетов, была сконструирована в 1779 году выдающимся английским механиком Дж.Уаттом.
Линейка Уатта - первая универсальная логарифмическая линейка, пригодная для выполнения любых инженерных расчетов, была сконструирована в 1779 году выдающимся английским механиком Дж.Уаттом.
Логарифмическая линейка (1657 год)
Слайд 34Вычислите с помощью логарифмической линейки
32
52
72
92
= 9
= 25
= 49
= 81
33
63
83
93
= 27
=
216
= 512
= 729
= 512
= 729
= 2,64
=7,75
= 6,7
=5,3
=9,5
=6,5
Слайд 36Готфрид Вильгельм Лейбниц (1646 – 1716)
О Лейбниц, о мудрец, создатель вещих
книг!
Ты выше мира был, как древние пророки.
Твой век, дивясь тебе, пророчеств не постиг
И с лестью смешивал безумные упрёки.
В. Брюсов
Ты выше мира был, как древние пророки.
Твой век, дивясь тебе, пророчеств не постиг
И с лестью смешивал безумные упрёки.
В. Брюсов
Слайд 37Деятельность
Лейбница
Сначала он хотел лишь улучшить машину великого Паскаля. Первое описание
подобного «арифметического инструмента» Лейбниц сделал ещё в 1670 г.
Через два года он предложил новое описание, по которому был изготовлен экземпляр, продемонстрированный в феврале 1673 г.
По словам самого учёного, он придумал арифмометр, чтобы надёжно и быстро механически выполнять все арифметические действия, особенно умножение. Однако признавал, что инструмент несовершенен, и обещал его улучшить.
Через два года он предложил новое описание, по которому был изготовлен экземпляр, продемонстрированный в феврале 1673 г.
По словам самого учёного, он придумал арифмометр, чтобы надёжно и быстро механически выполнять все арифметические действия, особенно умножение. Однако признавал, что инструмент несовершенен, и обещал его улучшить.
Слайд 38Лейбниц гордился своим изобретением. Вот что он писал:
«Мне посчастливилось построить
такую арифметическую машину, которая бесконечно отличается от машины Паскаля, так как моя машина даёт возможность совершать и умножение, и деление над огромными числами мгновенно, притом не прибегая к последовательному сложению и вычитанию».
Слайд 39Помощь России
По просьбе Петра I учёный разработал проекты развития образования и
государствен-ного управления в России.
«Я не принадлежу к числу тех,— писал Лейбниц русско-му царю, — которые питают страсть к своему отечеству или к какой-либо другой нации, мои помыслы направлены на благо всего человеческого рода... и мне приятнее сделать много добра у русских, чем мало у немцев...»
«Я не принадлежу к числу тех,— писал Лейбниц русско-му царю, — которые питают страсть к своему отечеству или к какой-либо другой нации, мои помыслы направлены на благо всего человеческого рода... и мне приятнее сделать много добра у русских, чем мало у немцев...»
Слайд 40Заслуги
Лейбница
Заслуга Готфрида Вильгельма Лейбница ещё и в том, что он
ввёл много математических терминов, прочно утвердившихся в научной практике: «функция», «дифференциал», «диф-ференциальное исчисление», «дифференциаль-ное уравнение», «алгоритм», «абсцисса», «орди-ната», «координата», а также
знаки дифференциала, инте-
грала, логическую символику.
Впервые использовал двоичную
систему счисления
знаки дифференциала, инте-
грала, логическую символику.
Впервые использовал двоичную
систему счисления
Слайд 41Чарлз Бэббидж
(1792-1871)
«Я отдаю себе отчёт, что
мои утверждения могут
рассматриваться как нечто
сверхутопическое и что они
вызовут в памяти филосо-
фов Лапуты...» — с грустью
признавался выдающийся
английский учёный Чарлз Бэббидж.
(Лапута — летающий остров, придуманный Джонатаном Свифтом. Там жили мудрецы, примечательные своей оторванностью от реальной жизни и пространными псевдонаучными рассуждениями.)
Слайд 42Создание разностной
машины
В 1822 г. Бэббидж закончил
описание разностной машины,
которая смогла бы
производить
вычисления с точностью до 18-го знака. Чертёж лёг на стол премьер-министра. В 1823 г. была выплачена первая субсидия на её постройку. Строительство продолжалось десять лет, конструкция машины всё более усложнялась.
вычисления с точностью до 18-го знака. Чертёж лёг на стол премьер-министра. В 1823 г. была выплачена первая субсидия на её постройку. Строительство продолжалось десять лет, конструкция машины всё более усложнялась.
Слайд 43Аналитическая
машина
В 1834 г. у него возникла
мысль создать универсаль-
ную вычислительную маши-
ну,
которую он назвал
аналитической. В этом проекте Бэббидж впервые пришёл к идее программного управления вычислительным процессом. Он задумал сделать механическое устройство, способное не просто считать, но и управлять ходом собственной работы в зависимости от заложенной программы и результатов промежуточных вычислений. Это изобретение опередило свою эпоху на 100 лет!
аналитической. В этом проекте Бэббидж впервые пришёл к идее программного управления вычислительным процессом. Он задумал сделать механическое устройство, способное не просто считать, но и управлять ходом собственной работы в зависимости от заложенной программы и результатов промежуточных вычислений. Это изобретение опередило свою эпоху на 100 лет!
Слайд 44
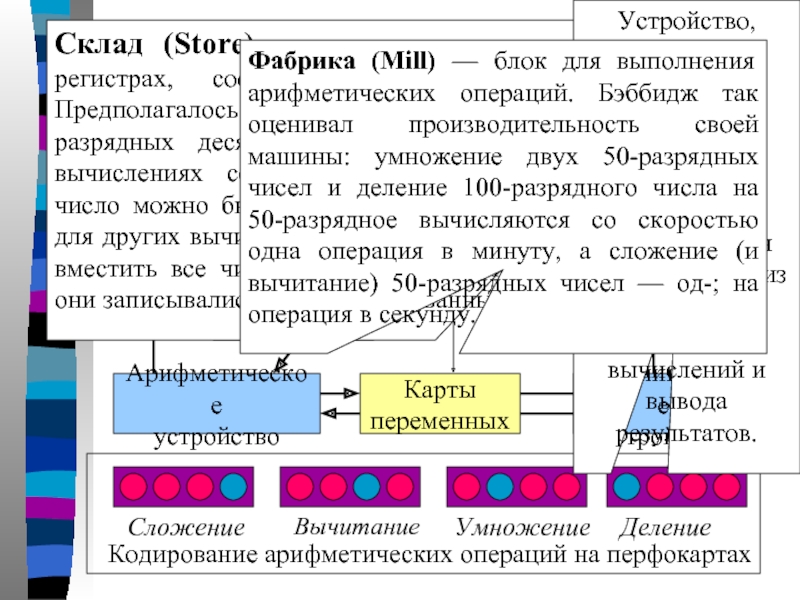
Схема работы аналитических машин
Устройства
ввода-вывода
Устройства
управления
Цифровые
карты
Карты
операции
Арифметическое
устройство
Карты
переменных
Запоминающее
устройство
Кодирование арифметических операций на
перфокартах
Склад (Store) — память для хранения чисел на регистрах, состоящих из механических колёс. Предполагалось, что память должна хранить тысячу 50-разрядных десятичных чисел. Если в дальнейших вычислениях содержимое регистра не требовалось, число можно было напечатать и использовать регистр для других вычислений. Если памяти не хватало, чтобы вместить все числа, необходимые для вычисления, то они записывались на перфорированные карты.
Устройство, оставленное автором без названия, для управления процессом вычисления, осуществления выборки чисел из памяти, выполнения вычислений и вывода результатов.
Фабрика (Mill) — блок для выполнения арифметических операций. Бэббидж так оценивал производительность своей машины: умножение двух 50-разрядных чисел и деление 100-разрядного числа на 50-разрядное вычисляются со скоростью одна операция в минуту, а сложение (и вычитание) 50-разрядных чисел — од-; на операция в секунду.
Слайд 45Перфокарты в
машине
Операционные—для
выполнения арифметических
операций
Управляющие — для осуществления загрузки чисел
из регистров в арифметическое устройство и выгрузки обратно в память, а также ввода-вывода.
Слайд 46 Соратница Бэббиджа Ада Августа
Лавлейс предложила назвать
перфокарты, управляющие
передачей чисел в машине,
переменными:
• «нулевая карта» загружает числа из регистра в арифметическое устройство, при этом содержимое регистра очищается;
• «удерживающая карта» производит то же действие, что и «нулевая карта», только содержимое регистра сохраняется;
• «доставляющая карта» передаёт результат из арифметического устройства обратно в память.
Карты, применяемые для ввода чисел в память назывались цифровыми.
Слайд 47Задумка
аналитической
машины
Возможности такой ма-
шины потрясли самого автора.
В мае 1835
г. учёный писал:
«Шесть месяцев я составлял проект машины более совершенной, чем первая. Я сам поражён той вычислительной мощностью, которой она будет обладать, ещё год назад я не смог бы в это поверить».
«Шесть месяцев я составлял проект машины более совершенной, чем первая. Я сам поражён той вычислительной мощностью, которой она будет обладать, ещё год назад я не смог бы в это поверить».
Слайд 48Аналитическая
машина
Бэббиджа
В аналитической машине
предусматривались все
основные элементы,
присущие современным компьютерам:
Склад — память,
Фабрика — арифметическое устройство процессора,
устройство для управления — управляющее устройство процессора.
Архитектура машины практически соответствует архитектуре современных ЭВМ.
Поэтому машину Бэббиджа хочется назвать первым настоящим компьютером.
Слайд 49Создание
арифмометра
(1880)
Вильгодт Теофилович
Однер, швед по национальности, жил в Санкт-Петербурге
и работал мастером экспедиции, выпускающей государственные денежные и ценные бумаги. Все свои патентованные изобретения он сделал в России: механических способ нумерации денежных знаков, машинка для изготовления папирос, механический ящик для тайного голосования, турникеты.
Слайд 50Вычислите с помощью арифмометра
57962+1643
65975+365
123456+99996
1324 * 6
64537 * 9
= 59602
= 66340
=356907
=7944
=580833
Слайд 52Герман Холлерит
29 февраля I860 г. в американ-
ском городе Буффало в семье
немецких иммигрантов Холлеритов
родился сын, Герман с
неприятным заболеванием —
дисграфией с трудом писал. Муче-
ния на уроках грамматики в конце концов вынудили его в возрасте 14 лет оставить школу. Спустя год поступил в Горную школу при Колумбийском университете.
На способного юношу обратил внимание один из преподавателей и пригласил после окончания школы в 1879 г. на работу в возглавляемое им Национальное бюро по переписи населения.
родился сын, Герман с
неприятным заболеванием —
дисграфией с трудом писал. Муче-
ния на уроках грамматики в конце концов вынудили его в возрасте 14 лет оставить школу. Спустя год поступил в Горную школу при Колумбийском университете.
На способного юношу обратил внимание один из преподавателей и пригласил после окончания школы в 1879 г. на работу в возглавляемое им Национальное бюро по переписи населения.
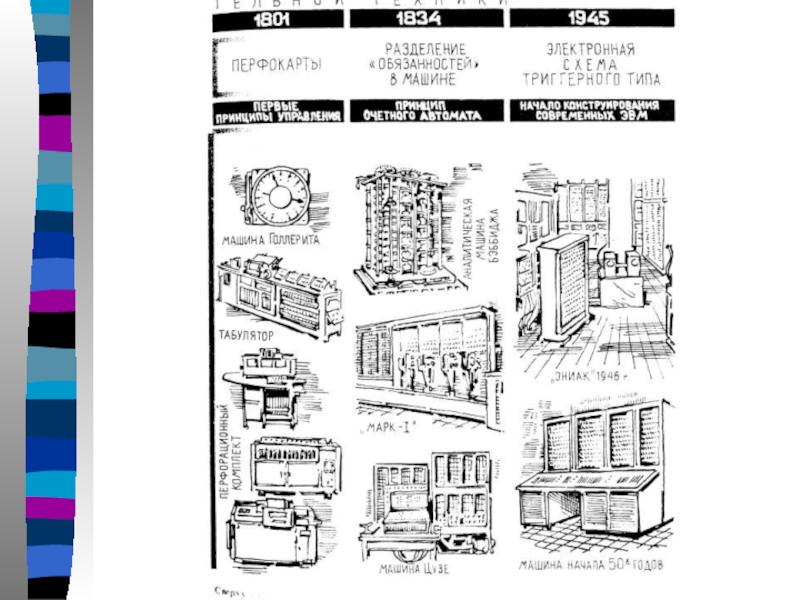
Слайд 53Табулятор Холлерита для переписи населения
Первый табулятор был опробован в 1887 г.
в статистическом бюро Балтимора. Результаты оказались весьма обнадёживающими, и через два года состоялось ещё одно испытание — частичная перепись населения в Сент-Луисе. Выигрыш во времени по сравнению с ручным подсчётом был двукратным, а на некоторых участках работы — десятикратным! Правительство заключило с Холлеритом контракт на поставку оборудования, и уже в июне 1890 г. началась первая в истории перепись населения с применением машин.
Слайд 54Табулятор Холлерита
Обработка результатов перепеси населеня, занесённых на 62 млн карточек, заняла
менее двух лет, а экономия составила 5 млн долларов-
огромную сумму, ведь
государственный бюджет США не
превышал тогда 100 млн долларов. Система Холлерита не только обеспечивала высокую скорость, но и позволяла сравнивать статистические данные по самым разным параметрам.
огромную сумму, ведь
государственный бюджет США не
превышал тогда 100 млн долларов. Система Холлерита не только обеспечивала высокую скорость, но и позволяла сравнивать статистические данные по самым разным параметрам.
Слайд 55Применение
табулятора
В 1896 г. Холлерит
основал компанию Tabulating Machine Company (ТМС).
Его машины применялись повсюду: на железных дорогах и промышленных предприятиях, в крупных торговых фирмах и страховых компаниях. С их помощью начисляли заработную плату и вели складской учёт, решали множество других задач.
Слайд 56Состав машины Холлерита
Машину для сортировки,
которая представляла собой набор ящиков с
крышками (карты продвигались по своеобразному конвейеру; с одной стороны карты находились считывающие штыри на пружинах, с другой – резервуар со ртутью; когда штырь попадал в отверстие на перфокарте, то благодаря пружине слегка касался ртути, находившейся на другой стороне, открывая крышку соответствующего ящика; туда и попадала перфокарта)
Клавишный перфоратор, позволяющий пробивать (перфорировать) около 100 отверстий в минуту одновременно на нескольких картах
Табулятор, который работал аналогичным образом, только замыкание электрической цепи приводило к увеличению показаний соответствующего счётчика на единицу
Слайд 61Список использованных источников
http://museum.iu4.bmstu.ru/firststeps/letters.shtml - музей информатики
http://www.mycomp.com.ua/ - история ВТ
http://fem.grsu.by/other/001/begin история ВТ
http://www.fio.by/vypusk/Potok_72/group_3/user_3/subpages/pal.htm
- история
http://www.websib.ru/noos/informatika/comphistory/drhistory/schet.htm история
http://www.math.dcn-asu.ru/external/users/~ternovoi/ira/glava_3.html математический факультет АлтГУ - история ВТ
http://www.websib.ru/noos/informatika/comphistory/drhistory/schet.htm история
http://www.math.dcn-asu.ru/external/users/~ternovoi/ira/glava_3.html математический факультет АлтГУ - история ВТ
Слайд 62Список использованной литературы
Энциклопедия для детей. Т.11. Математика /Глав.ред. М.Д. Аксёнова –
М.: Аванта+,2000 – 688 с.
Энциклопедия для детей. Т.22. Информатика /Глав.ред. М.Д. Аксёнова – М.: Аванта+,2000 – 620 с.
Пекелис В.Д., Кибернетика от А до Я: Маленькая энциклопедия / Худож. Б. Белов и А. Лебедев. – М.: Дет. Лит., 1990. – 479 с.
Энциклопедия для детей. Т.22. Информатика /Глав.ред. М.Д. Аксёнова – М.: Аванта+,2000 – 620 с.
Пекелис В.Д., Кибернетика от А до Я: Маленькая энциклопедия / Худож. Б. Белов и А. Лебедев. – М.: Дет. Лит., 1990. – 479 с.
