- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Исследования скважин и пластов презентация
Содержание
- 1. Исследования скважин и пластов
- 2. Уравнение пьезопроводности
- 3. Сжимаемость
- 4. Предположения уравнения при выводе уравнения фильтрации Радиальный
- 5. Безразмерные переменные Безразмерные переменные позволяют выделить переменные
- 6. Безразмерные переменные Безразмерные переменные для практических метрических
- 7. Решение уравнения фильтрации Для того чтобы найти
- 8. Решение линейного стока Начальное условие Условие постоянного
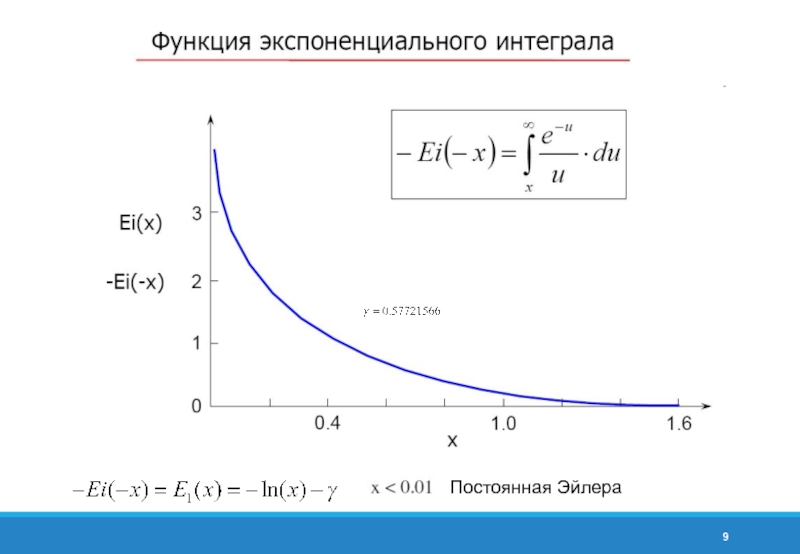
- 9. Постоянная Эйлера
- 10. Постоянная Эйлера—Маскерони Постоянная Эйлера—Маскерони Материал из
- 11. Решение линейного стока Логарифмическая аппроксимация решения Логарифмическая аппроксимация имеет место при
- 12. Применимость решения линейного стока Решение линейного стока в размерных переменных
- 13. Применимость решения линейного стока Решение линейного стока в практических метрических переменных
- 14. Упражнение Построить в Excel решение линейного стока
- 15. Применимость решения линейного стока Для бесконечного однородного
- 16. Решение в полулогарифмических координатах Логарифмическое приближение для
- 17. Радиус исследований Радиус исследований – показывает расстояние
- 18. Упражнение. Радиус исследований
- 19. Скин-фактор скважины Скин-фактор описывает изменение проницаемости призабойной
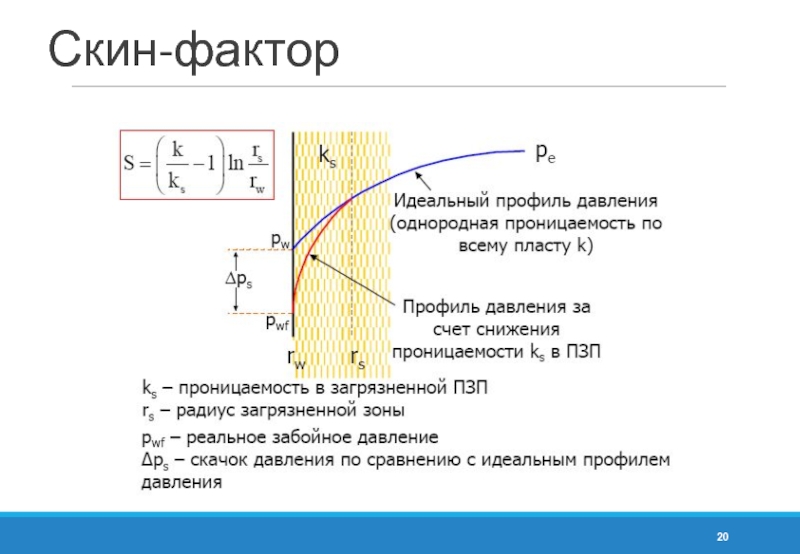
- 20. Скин-фактор
- 21. Скин-фактор Скин-фактор в уравнении установившегося притока в радиальном пласте Продуктивность скважины определяется как
- 22. Упражнение. Влияние скина на решение Скин-фактор создает
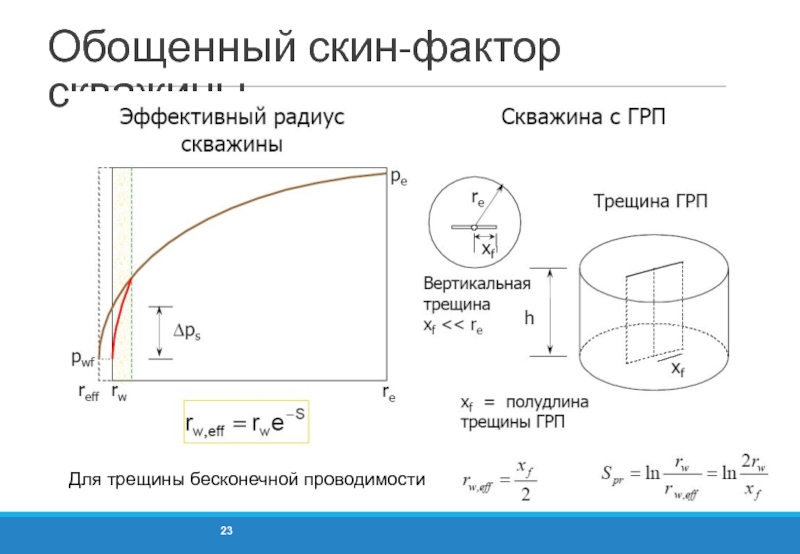
- 23. Обощенный скин-фактор скважины Для трещины бесконечной проводимости
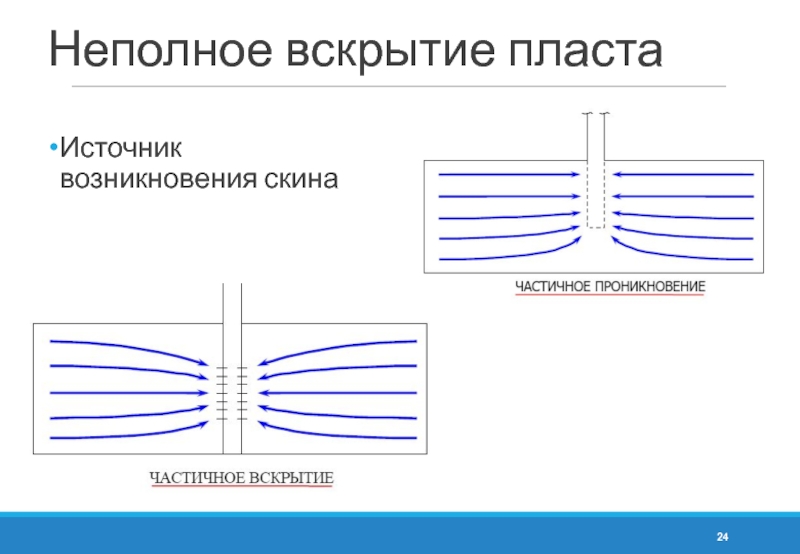
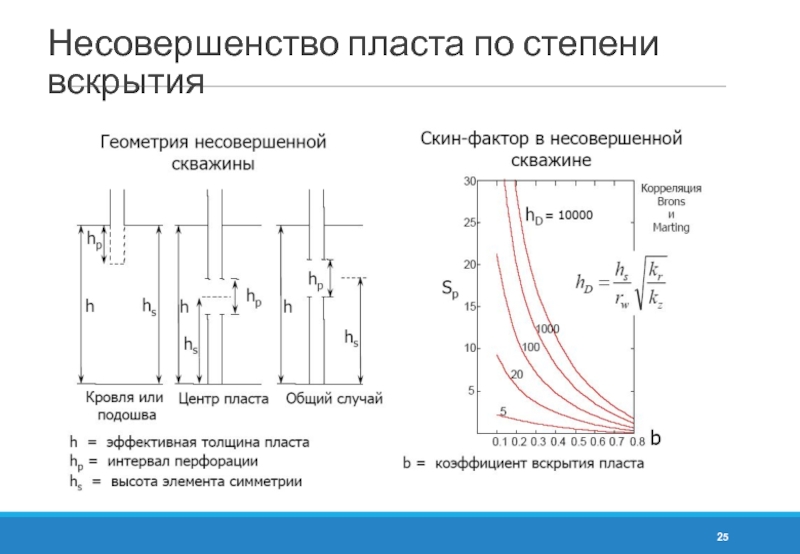
- 24. Неполное вскрытие пласта Источник возникновения скина
- 25. Несовершенство пласта по степени вскрытия
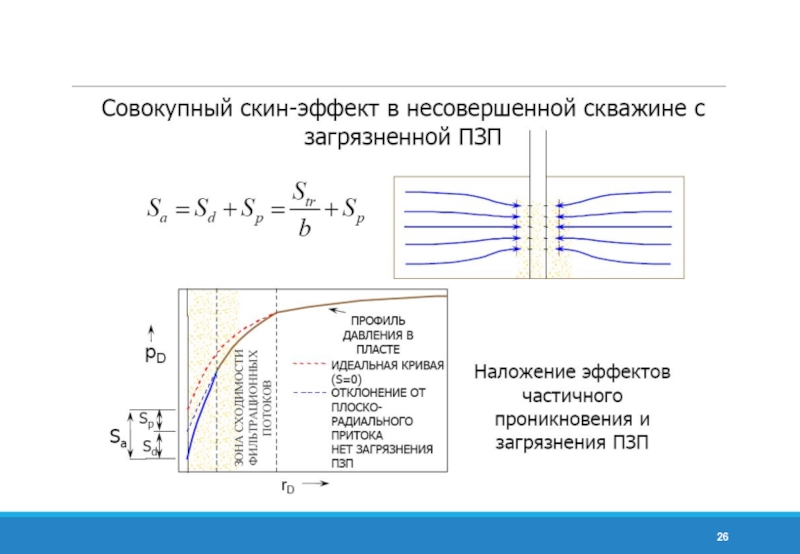
- 27. Обобщенный скин-фактор Stotal включает: SMеханический (загрязнение,
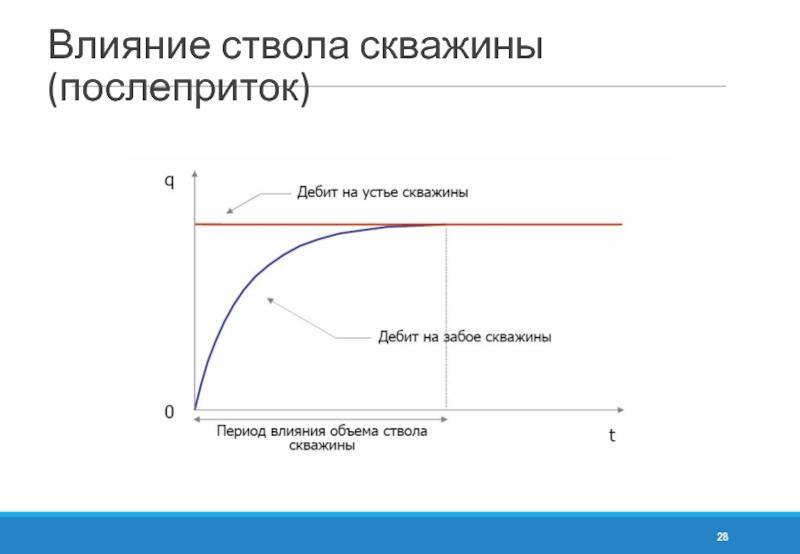
- 28. Влияние ствола скважины (послеприток)
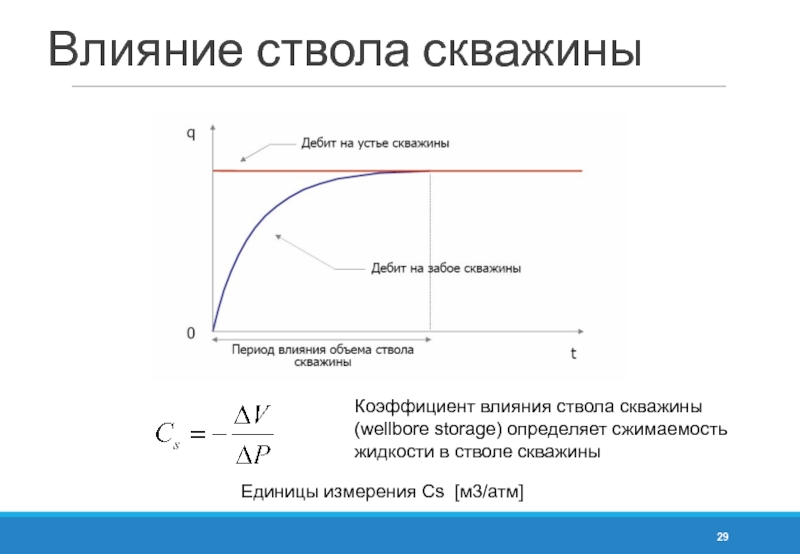
- 29. Влияние ствола скважины Коэффициент влияния ствола скважины
- 30. Влияние ствола скважины Для фонтанирующей скважины Изменение
- 31. Влияние ствола в фонтанирующей скважине Глубина скважины
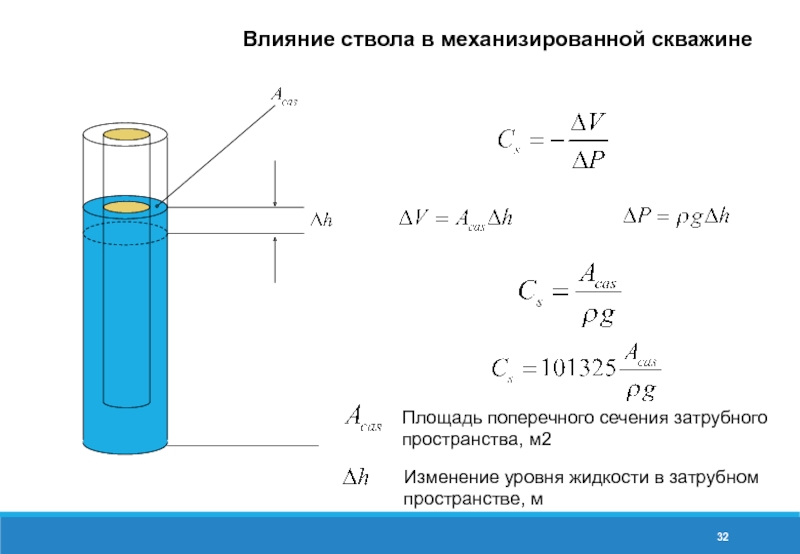
- 32. Влияние ствола в механизированной скважине Площадь поперечного
- 33. Влияние ствола в механизированной скважине Глубина скважины
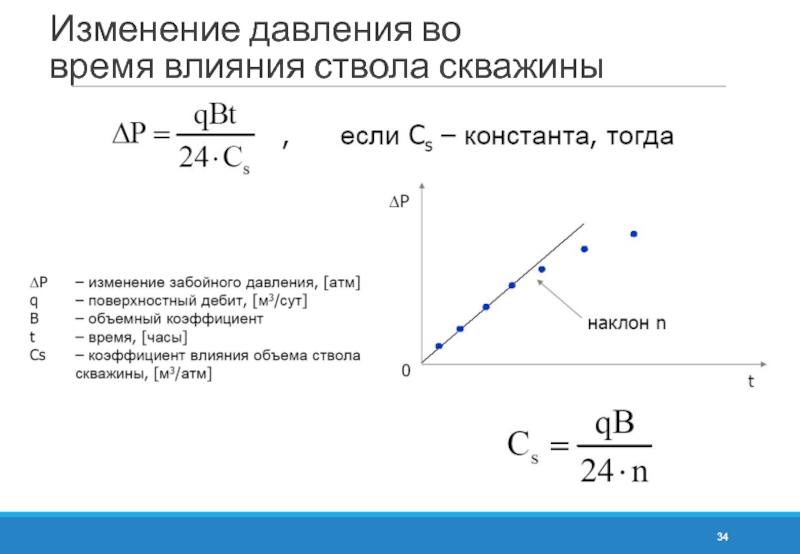
- 34. Изменение давления во время влияния ствола скважины
- 36. Приток из пласта
- 37. Определение периода влияния ствола скважины где
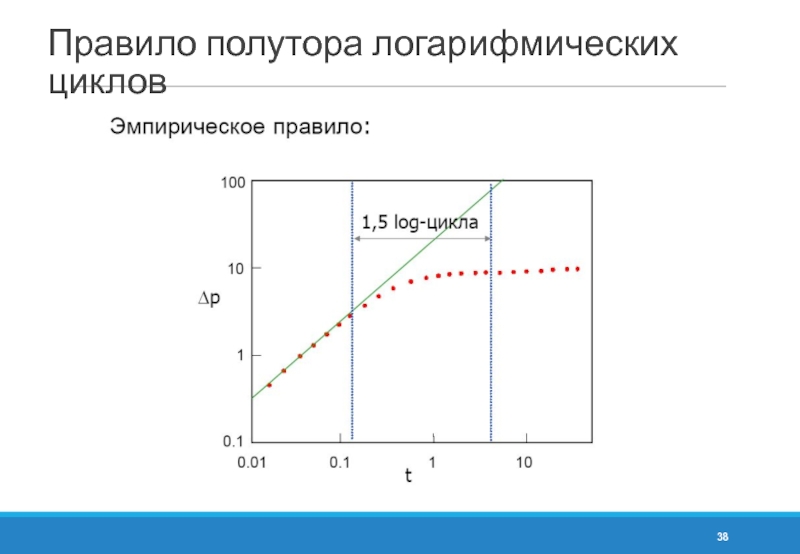
- 38. Правило полутора логарифмических циклов
- 39. Решение уравнения фильтрации Решение уравнения фильтрации для
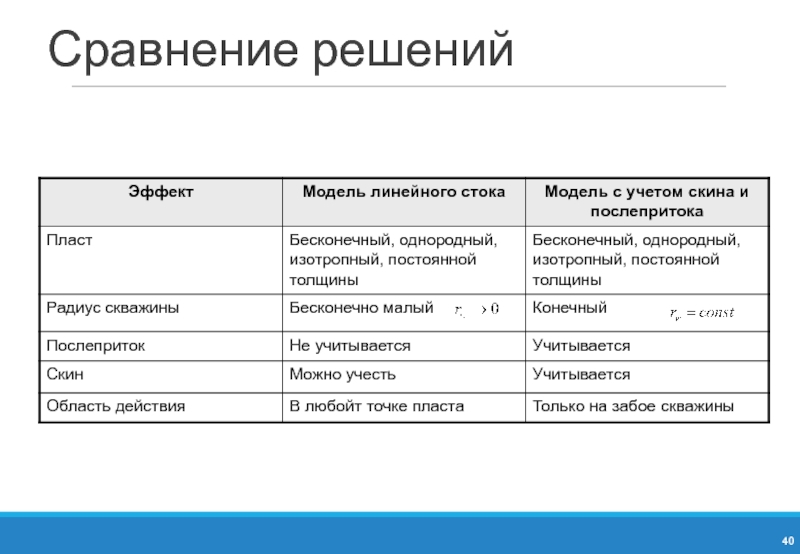
- 40. Сравнение решений
- 41. Упражнение Построить решение уравнения фильтрации для бесконечного
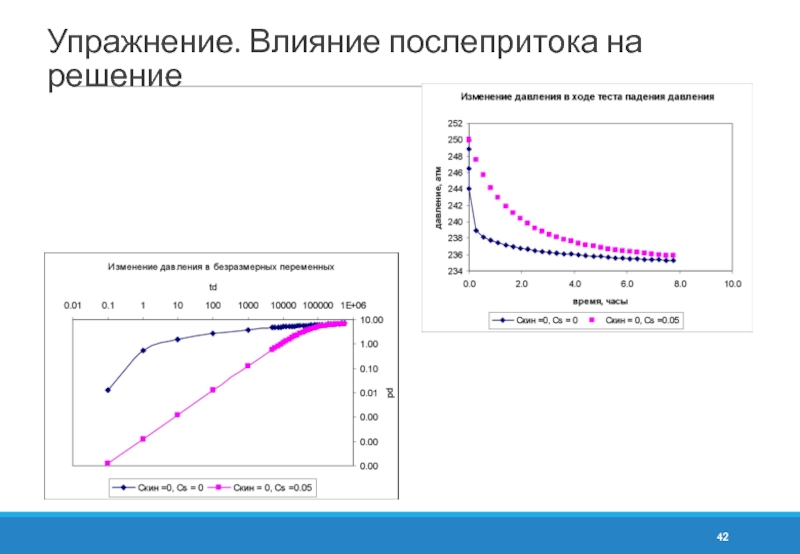
- 42. Упражнение. Влияние послепритока на решение
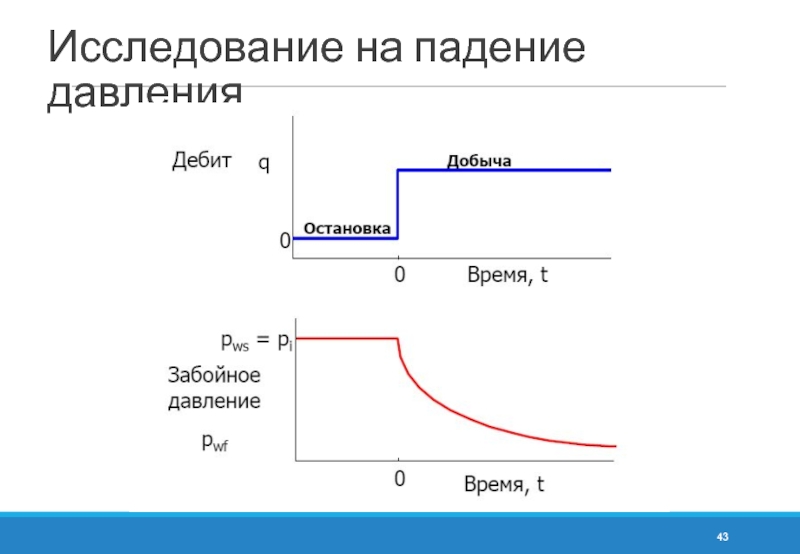
- 43. Исследование на падение давления
- 44. Применимость решения линейного стока Для бесконечного однородного
- 45. Решение в полулогарифмических координатах Логарифмическое приближение для
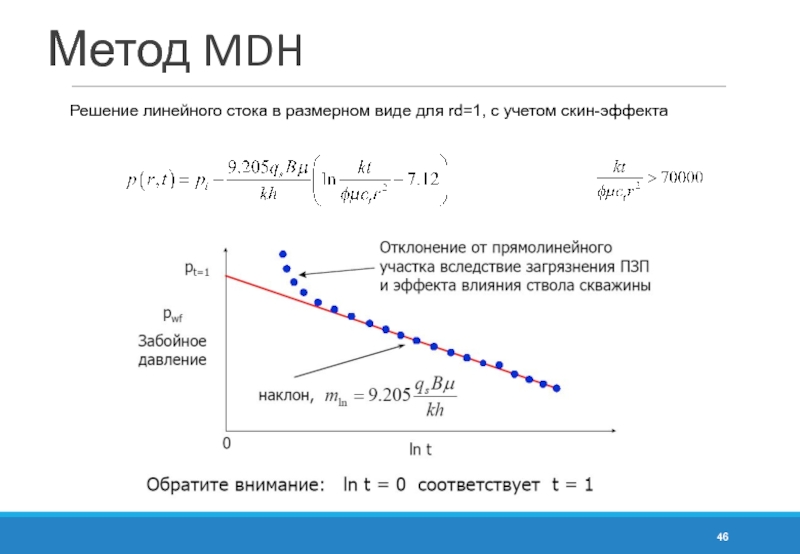
- 46. Метод MDH Решение линейного стока в размерном виде для rd=1, с учетом скин-эффекта
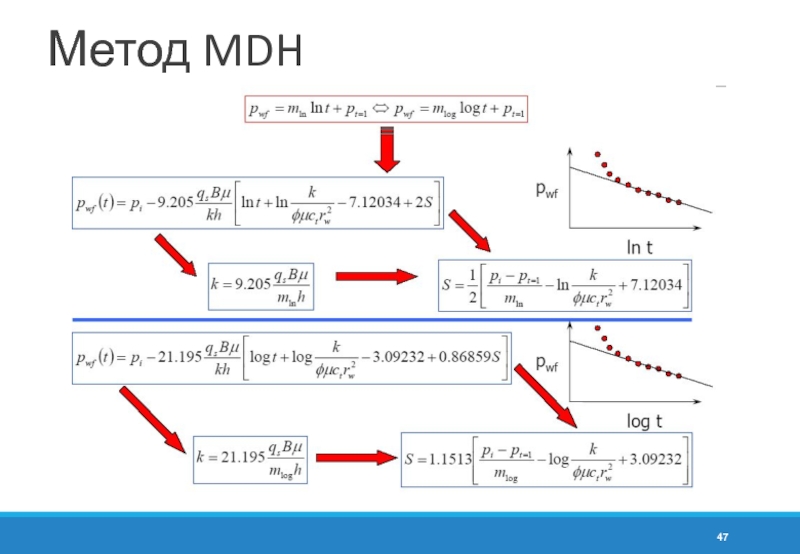
- 47. Метод MDH
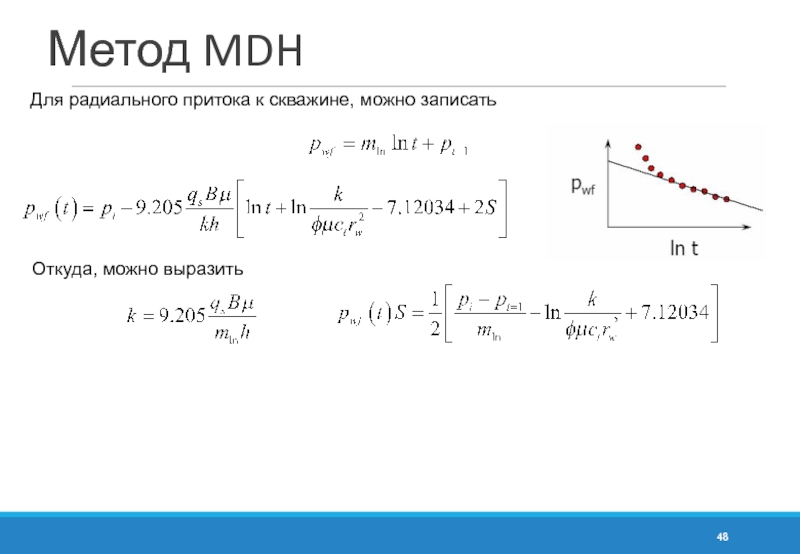
- 48. Метод MDH Для радиального притока к скважине, можно записать Откуда, можно выразить
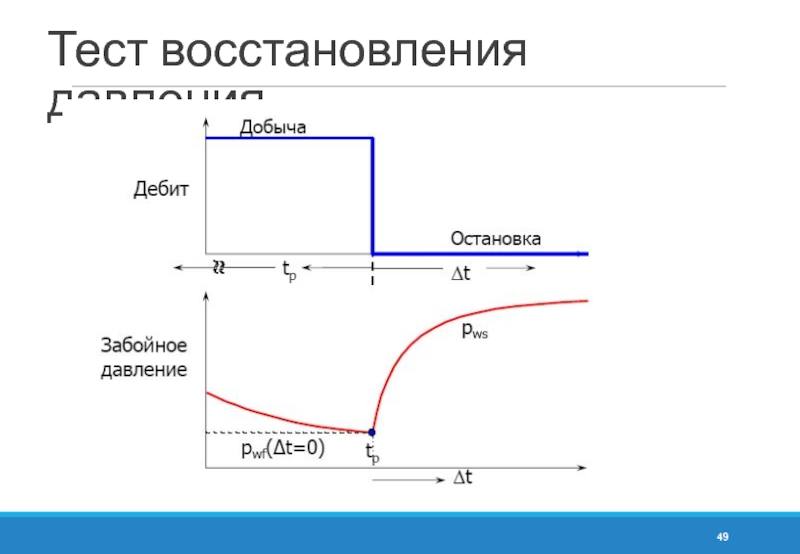
- 49. Тест восстановления давления
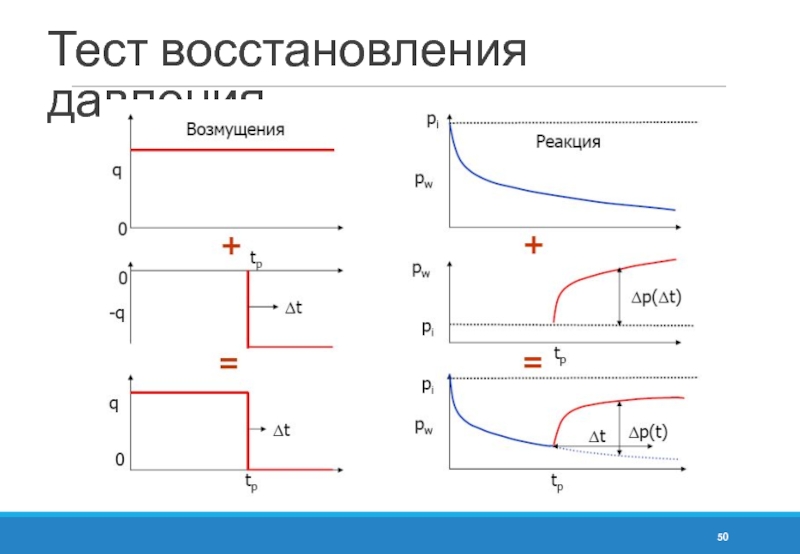
- 50. Тест восстановления давления
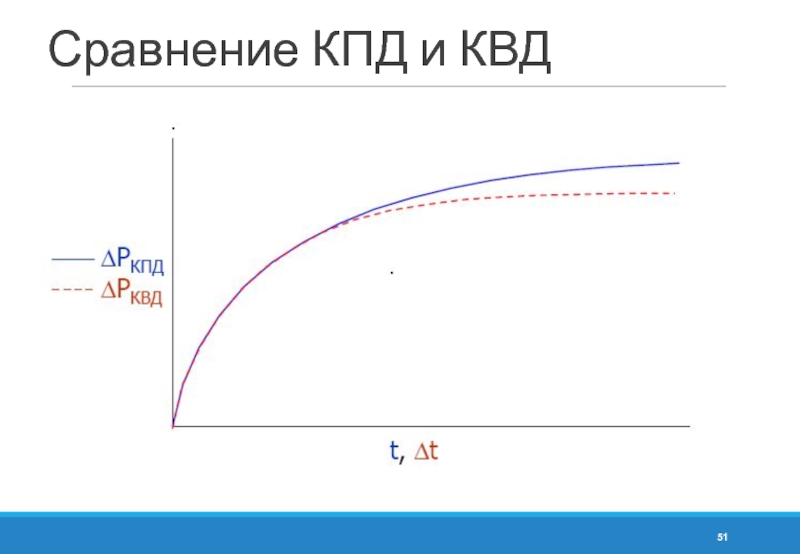
- 51. Сравнение КПД и КВД
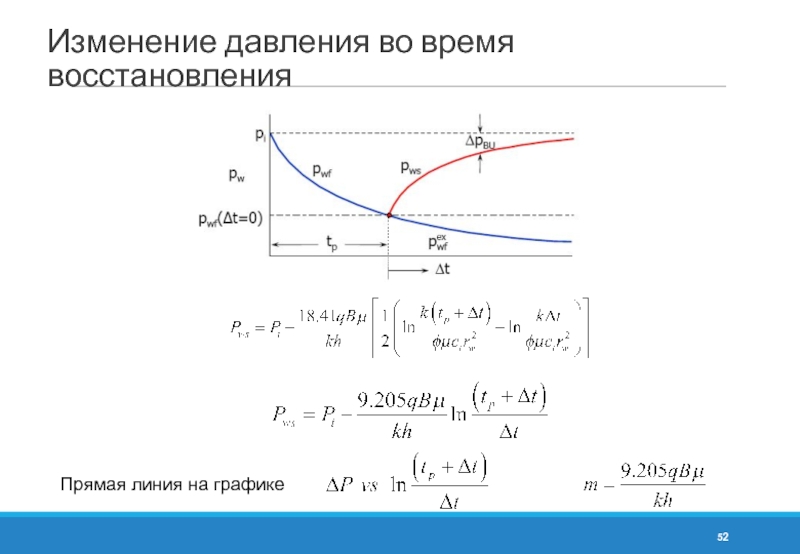
- 52. Изменение давления во время восстановления Прямая линия на графике
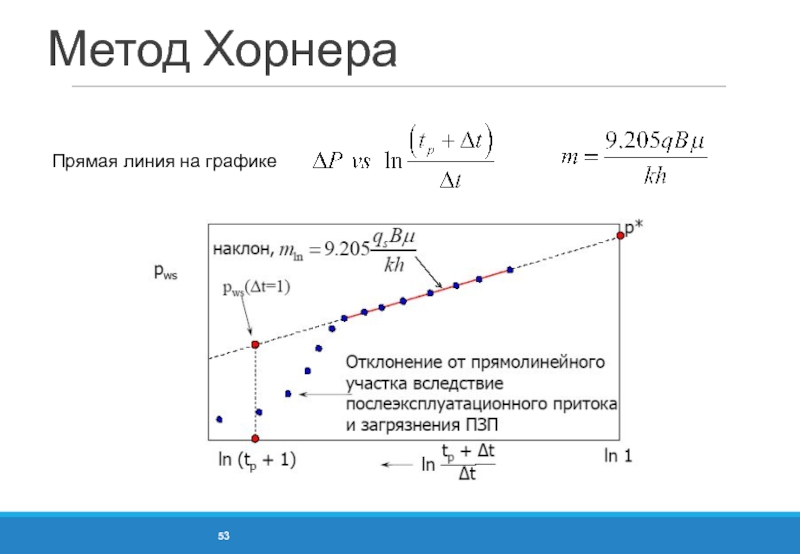
- 53. Метод Хорнера Прямая линия на графике
- 54. Вычисление скин-фактора по методу Хорнера
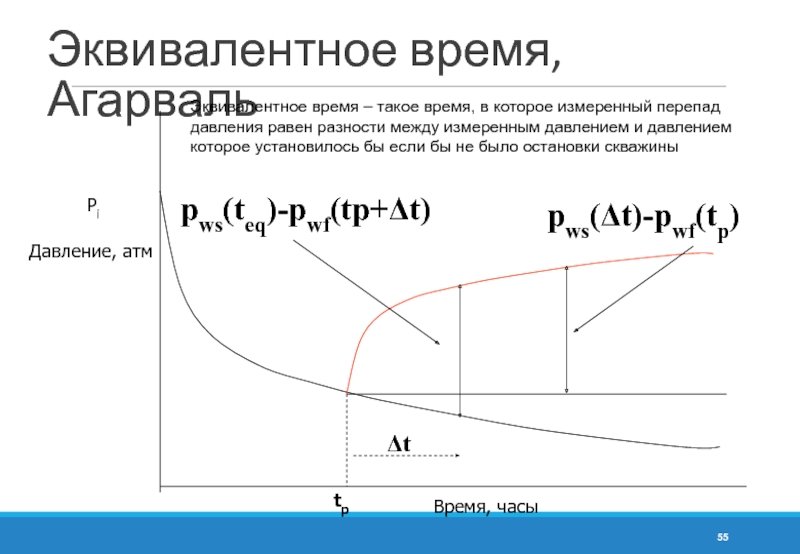
- 55. Эквивалентное время, Агарваль Давление, атм Pi
- 56. Эквивалентное время
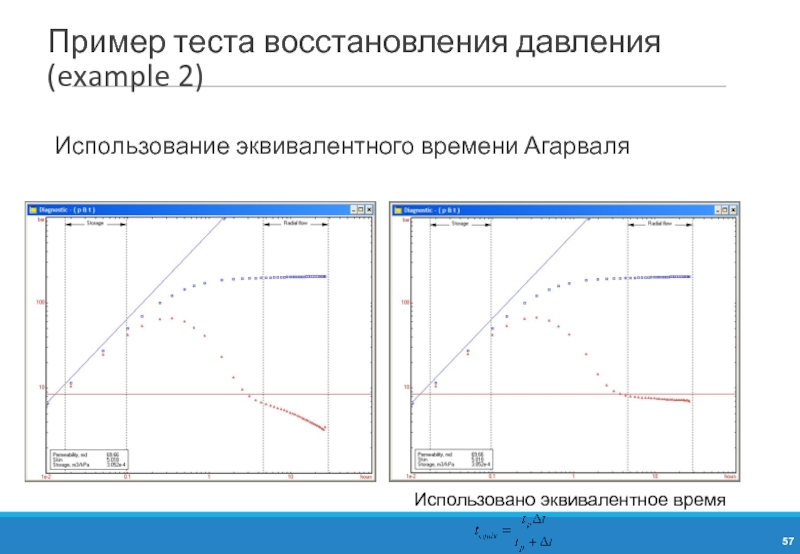
- 57. Пример теста восстановления давления (example 2) Использование эквивалентного времени Агарваля Использовано эквивалентное время
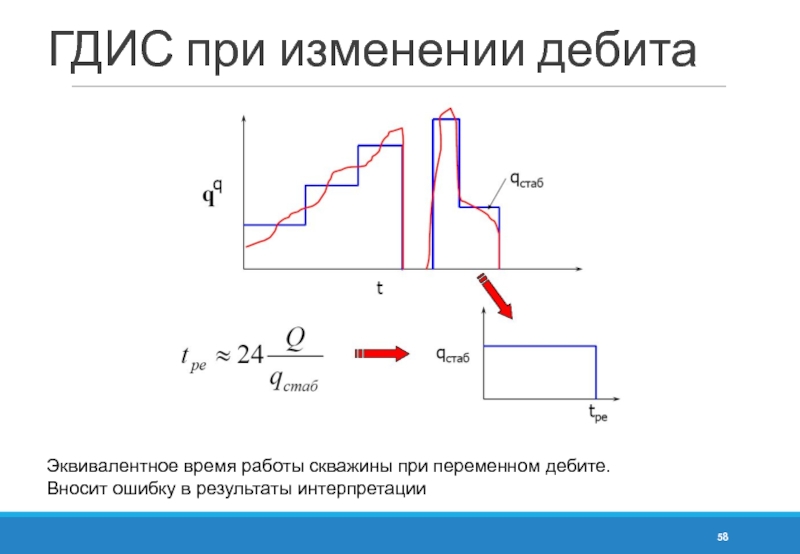
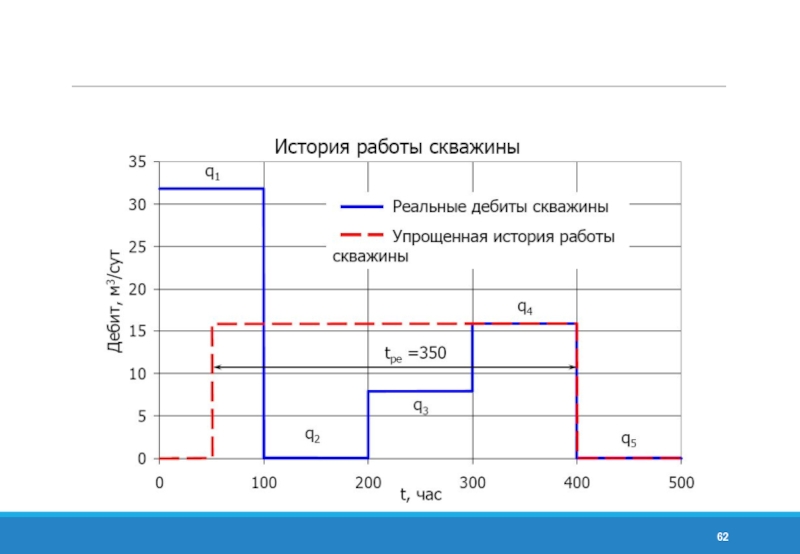
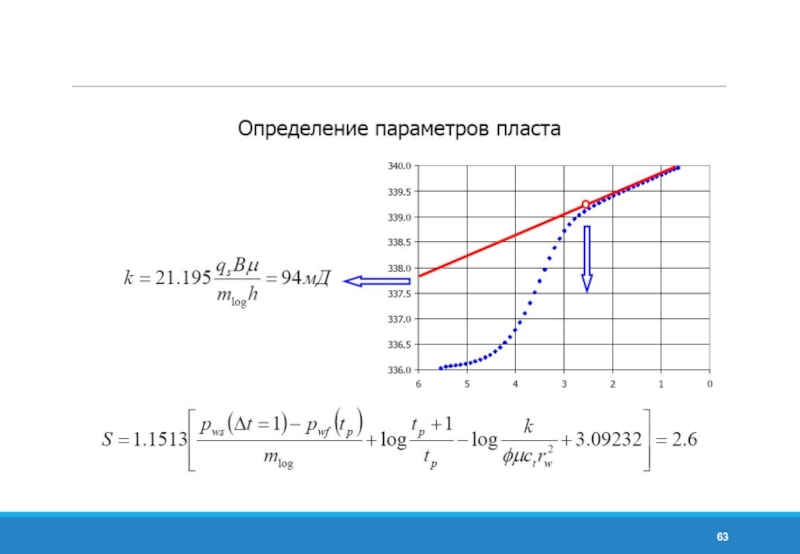
- 58. ГДИС при изменении дебита Эквивалентное время работы
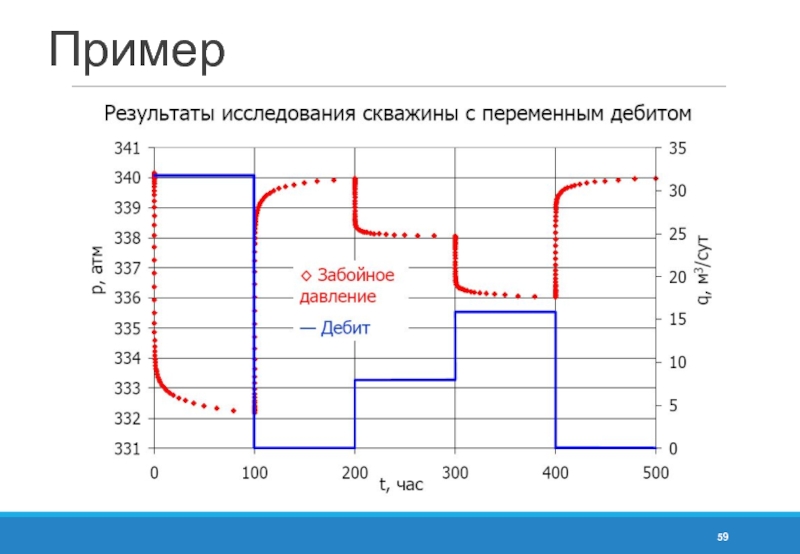
- 59. Пример
Слайд 4Предположения уравнения при выводе уравнения фильтрации
Радиальный режим притока по всей эффективной
толщине пласта
Однородный изотропный пласт постоянной толщины
Дебит и проницаемость пласта не зависят от давления
Сжимаемость мала и постоянна
Вязкость системы постоянна
Градиент давления мал
Гравитационные силы пренебрежимо малы
Однородный изотропный пласт постоянной толщины
Дебит и проницаемость пласта не зависят от давления
Сжимаемость мала и постоянна
Вязкость системы постоянна
Градиент давления мал
Гравитационные силы пренебрежимо малы
Слайд 5Безразмерные переменные
Безразмерные переменные позволяют выделить переменные влияющие на поведение системы и
избавиться от лишних неизвестных, производных от других величин
Уравнение записанное в безразмерных переменных не зависит от выбора системы размерностей
Уравнение записанное в безразмерных переменных не зависит от выбора системы размерностей
Решение уравнения фильтрации
Слайд 6Безразмерные переменные
Безразмерные переменные для практических метрических систем единиц
Безразмерное время
Безразмерное давление
Связанное с
радиусом скважины
Связанное с областью дренирования скважины
Связанное с размерами трещины
Безразмерный коэффициент ствола скважины
Слайд 7Решение уравнения фильтрации
Для того чтобы найти решение уравнения фильтрации необходимо задать
начальное и граничные условия
Задание начального и граничного условий – задает модель интерпретации ГДИС
Наиболее распространенные модели
Модель постоянного дебита
Модель постоянного давления
Модель линейного стока (маленький радиус скважины)
Модель замкнутого пласта
Модель пласта с поддержание давления на границе
Модель скважины с трещиной гидроразрыва
и т.д.
Задание начального и граничного условий – задает модель интерпретации ГДИС
Наиболее распространенные модели
Модель постоянного дебита
Модель постоянного давления
Модель линейного стока (маленький радиус скважины)
Модель замкнутого пласта
Модель пласта с поддержание давления на границе
Модель скважины с трещиной гидроразрыва
и т.д.
Слайд 8Решение линейного стока
Начальное условие
Условие постоянного дебита в скважине малого радиуса
Условие бесконечного
пласта
Решение линейного стока уравнения фильтрации
Слайд 10Постоянная Эйлера—Маскерони
Постоянная Эйлера—Маскерони
Материал из Википедии — свободной энциклопедии
Постоянная Э́йлера—Маскеро́ни или постоянная
Эйлера — математическая константа, определяемая как предел разности между частичной суммой гармонического ряда и натуральным логарифмом числа:
Константа введена Леонардом Эйлером в 1735, который предложил для неё обозначение C, которое до сих пор иногда применяется. Итальянский математик Лоренцо Маскерони в 1790 вычислил 32 знака константы и предложил современное обозначение γ.
Значение константы:
γ ≈ 0,577215664901532860606512090082402431042159335 9399235988057672348848677267776646709369470632917467495…
Постоянная Эйлера может быть выражена как интеграл:
Через неё выражается производная Гамма-функции, например, γ = − Γ'(1).
В теории чисел нередко используется константа
eγ ≈ 1,78107241799019798523650410310717954916964521430343…
Константа введена Леонардом Эйлером в 1735, который предложил для неё обозначение C, которое до сих пор иногда применяется. Итальянский математик Лоренцо Маскерони в 1790 вычислил 32 знака константы и предложил современное обозначение γ.
Значение константы:
γ ≈ 0,577215664901532860606512090082402431042159335 9399235988057672348848677267776646709369470632917467495…
Постоянная Эйлера может быть выражена как интеграл:
Через неё выражается производная Гамма-функции, например, γ = − Γ'(1).
В теории чисел нередко используется константа
eγ ≈ 1,78107241799019798523650410310717954916964521430343…
Слайд 11Решение линейного стока
Логарифмическая аппроксимация решения
Логарифмическая аппроксимация имеет место при
Слайд 13Применимость решения линейного стока
Решение линейного стока в практических метрических переменных
Слайд 14Упражнение
Построить в Excel решение линейного стока и его логарифмическую аппроксимацию
Представить полученные
решения в полулогарифмических координатах
Определить диапазон применимости логарифмической аппроксимации решения линейного стока с размерных и безразмерных переменных
Определить диапазон применимости логарифмической аппроксимации решения линейного стока с размерных и безразмерных переменных
Слайд 15Применимость решения линейного стока
Для бесконечного однородного пласта поведения давления при тесте
на падение давления описывается решением для линейного стока
Для практических метрических единиц
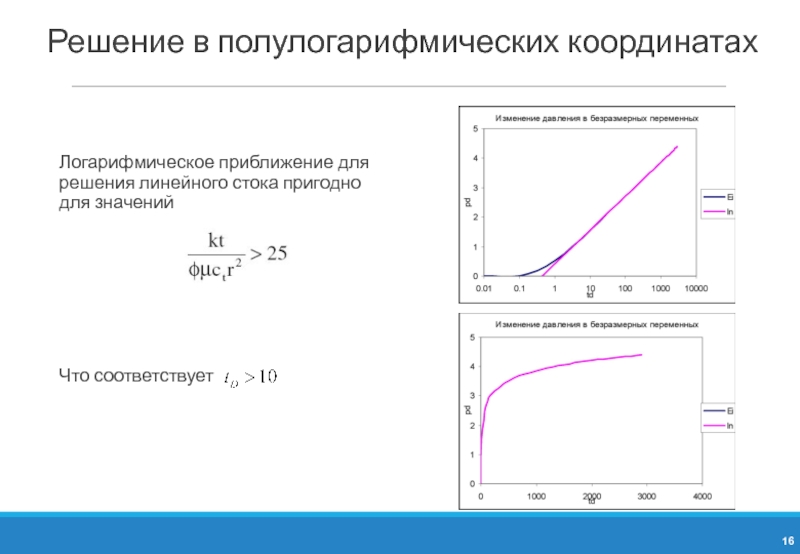
Слайд 16Решение в полулогарифмических координатах
Логарифмическое приближение для решения линейного стока пригодно для
значений
Что соответствует
Что соответствует
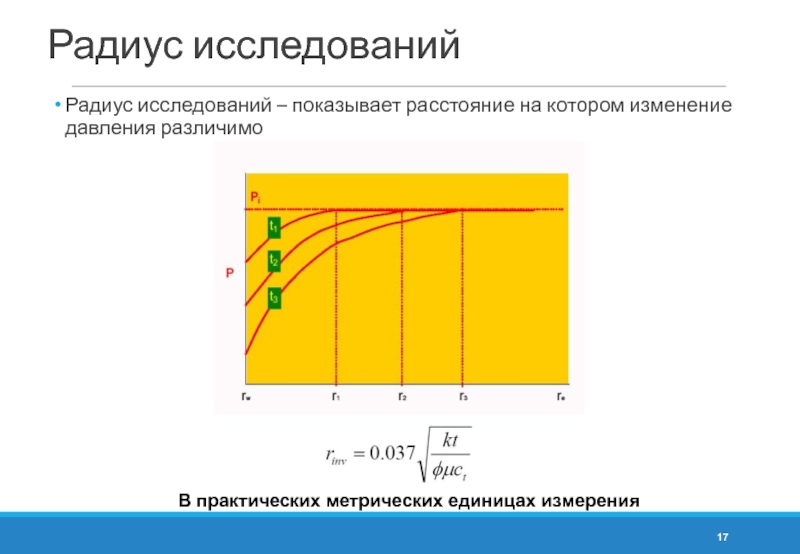
Слайд 17Радиус исследований
Радиус исследований – показывает расстояние на котором изменение давления различимо
В
практических метрических единицах измерения
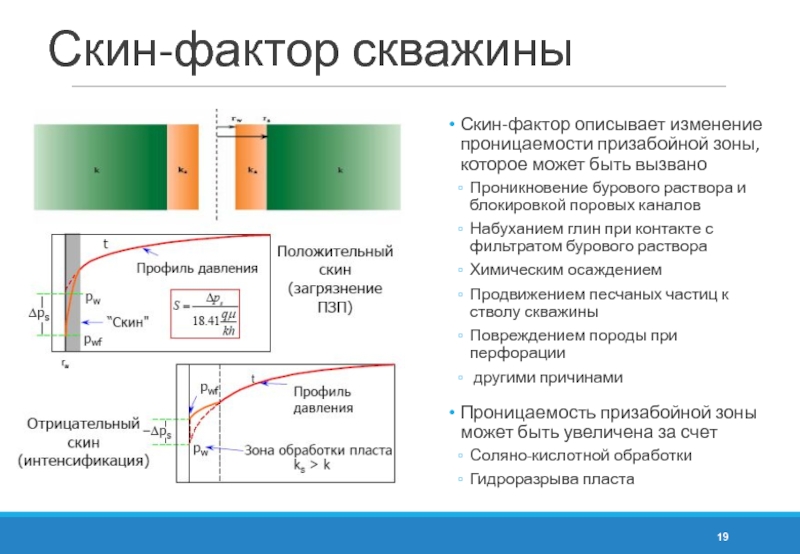
Слайд 19Скин-фактор скважины
Скин-фактор описывает изменение проницаемости призабойной зоны, которое может быть вызвано
Проникновение
бурового раствора и блокировкой поровых каналов
Набуханием глин при контакте с фильтратом бурового раствора
Химическим осаждением
Продвижением песчаных частиц к стволу скважины
Повреждением породы при перфорации
другими причинами
Проницаемость призабойной зоны может быть увеличена за счет
Соляно-кислотной обработки
Гидроразрыва пласта
Набуханием глин при контакте с фильтратом бурового раствора
Химическим осаждением
Продвижением песчаных частиц к стволу скважины
Повреждением породы при перфорации
другими причинами
Проницаемость призабойной зоны может быть увеличена за счет
Соляно-кислотной обработки
Гидроразрыва пласта
Слайд 21Скин-фактор
Скин-фактор в уравнении установившегося притока в радиальном пласте
Продуктивность скважины определяется как
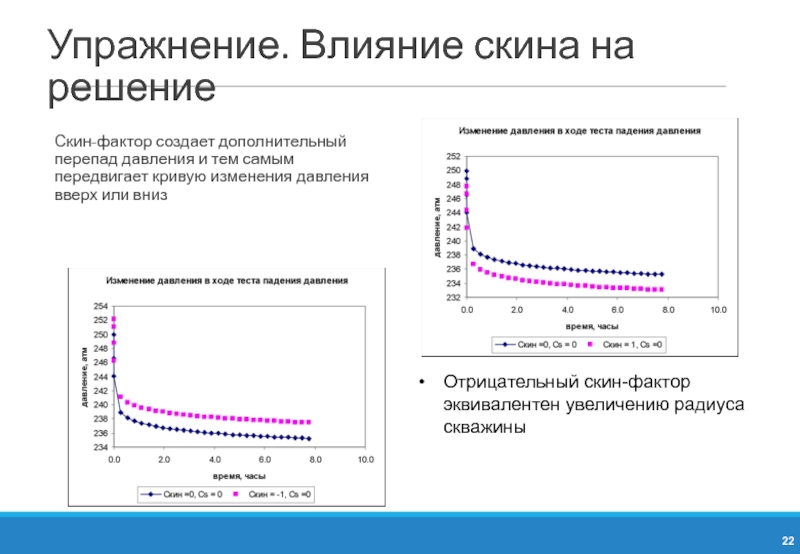
Слайд 22Упражнение. Влияние скина на решение
Скин-фактор создает дополнительный перепад давления и тем
самым передвигает кривую изменения давления вверх или вниз
Отрицательный скин-фактор эквивалентен увеличению радиуса скважины
Слайд 27Обобщенный скин-фактор
Stotal включает:
SMеханический (загрязнение, стимуляция)
SФлюиды (влияние газа, многофазного потока)
SЗаканчивания (трещины
гидроразрыва, частичное вскрытие, наклонные скважины)
SГеологический (анизотропия, естественная трещиноватость)
SГеологический (анизотропия, естественная трещиноватость)
Диапазоны изменения скин-фактора (по Грингартену)
SМеханический = -4 (после кислотной обработки) → +20 (загрязнение)
SГаз = +5 → +20
SМногофазный = +5 → +15
SAнизотропии = -2 → 0
SЗаканчивания = -5.5 (трещины, горизонтальные скважины) → +300 (неполное вскрытие)
Sгеологический = -3 (геоскин в трещиноватых коллекторах) → 0
Слайд 29Влияние ствола скважины
Коэффициент влияния ствола скважины
(wellbore storage) определяет сжимаемость
жидкости
в стволе скважины
Единицы измерения Cs [м3/атм]
Слайд 30Влияние ствола скважины
Для фонтанирующей скважины
Изменение объема жидкости в стволе скважины происходит
за счет сжимаемости жидкости
Единицы измерения Cs [м3/атм]
Объем жидкости в стволе скважины [м3]
Сжимаемость жидкости в стволе скважины [1/атм]
Для фонтанирующей скважины, коэффициент ствола скважины
Слайд 31Влияние ствола в фонтанирующей скважине
Глубина скважины 2000 м
Диаметр НКТ
70 мм
Сжимаемость жидкости в стволе скважины 1*10-5 1/атм
Сжимаемость жидкости в стволе скважины 1*10-5 1/атм
м3
[м3/атм]
Слайд 32Влияние ствола в механизированной скважине
Площадь поперечного сечения затрубного пространства, м2
Изменение уровня
жидкости в затрубном пространстве, м
Слайд 33Влияние ствола в механизированной скважине
Глубина скважины 2000 м
Диаметр НКТ
73 мм
Диаметр эксп. коллоны 137 мм
Плотность нефти 866 кг/м3
Диаметр эксп. коллоны 137 мм
Плотность нефти 866 кг/м3
м2
[м3/атм]
Чему равна величина коэффициента ствола скважины, если в затрубном пространстве находится газо-нефтая смесь плотностью 500 кг/м3?
Слайд 37Определение периода влияния ствола скважины
где
- проницаемость, [миллидарси];
– мощность пласта, [м];
– вязкость, [сП];
– скин-фактор;
- Правило Чена и Бригхама (Chen and Brigham)
- Правило Рамея (Ramey)
Существует три правила определения конца периода влияния ствола скважины
Слайд 39Решение уравнения фильтрации
Решение уравнения фильтрации для бесконечного пласта, конечного радиуса скважины
с учетом
скин – фактора и послепритока
Решение в пространстве Лапласа имеет вид
Решение в действительных переменных находится с использованием алгоритма Стефеста
Слайд 41Упражнение
Построить решение уравнения фильтрации для бесконечного пласта с учетом скин –
фактора и послепритока скважины в Excel с использованием функции Stehfest
Исследовать влияния скин-фактора на решение
Исследовать влияние послепритока в скважину на решение
Сравнить решение с решением линейного стока и его логарифмическим приближением
Исследовать влияния скин-фактора на решение
Исследовать влияние послепритока в скважину на решение
Сравнить решение с решением линейного стока и его логарифмическим приближением
Слайд 44Применимость решения линейного стока
Для бесконечного однородного пласта поведения давления при тесте
на падение давления описывается решением для линейного стока
Для практических метрических единиц
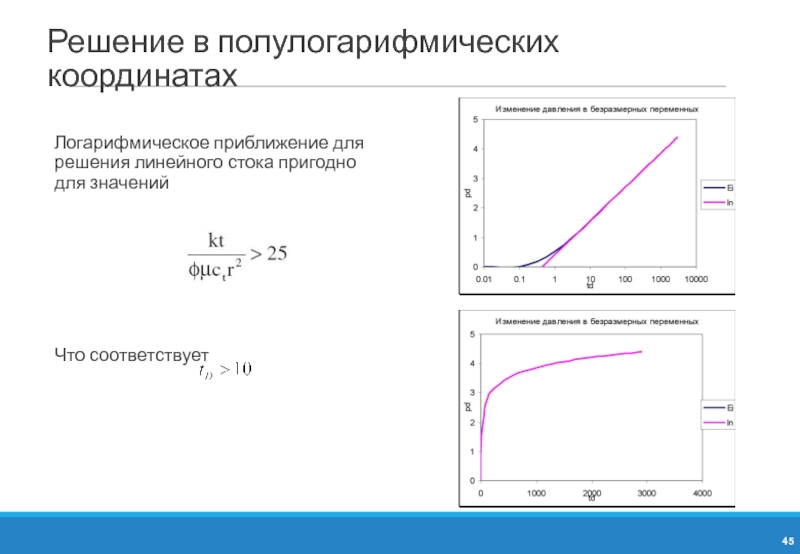
Слайд 45Решение в полулогарифмических координатах
Логарифмическое приближение для решения линейного стока пригодно для
значений
Что соответствует
Что соответствует
Слайд 55Эквивалентное время, Агарваль
Давление, атм
Pi
Время, часы
tp
Δt
pws(Δt)-pwf(tp)
pws(teq)-pwf(tp+Δt)
Эквивалентное время – такое время, в которое
измеренный перепад давления равен разности между измеренным давлением и давлением которое установилось бы если бы не было остановки скважины
Слайд 57Пример теста восстановления давления (example 2)
Использование эквивалентного времени Агарваля
Использовано эквивалентное время
Слайд 58ГДИС при изменении дебита
Эквивалентное время работы скважины при переменном дебите.
Вносит ошибку
в результаты интерпретации
