- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Исследование функций на монотонность и экстремумы с помощью производной. презентация
Содержание
Слайд 2 Промежутки возрастания и убывания – промежутки
монотонности.
Достаточный признак убывания : если f’ (x)< 0, то f (x) убывает на на данном промежутке.
Достаточный признак возрастания : если f’ (x)> 0, то f (x) возрастает на на данном промежутке.
Слайд 3 Пример. f
(x)= x4-8x2
1) D (f)= (-∞; +∞), функция непрерывна и дифференцируема на D(f).
2) f’ (x)= 4x3-16x
f’ (x)=0, если 4x3 -16x=0
4х(х-2)(х+2)=0
Слайд 6Решение упражнений стр. 131 №854,856 ( устно) №862 ( а, б), 865 (
а, в)
Домашнее задание:
№ 863, № 864 ( а, б), № 865 ( б,г),№ 866 ( а, б).



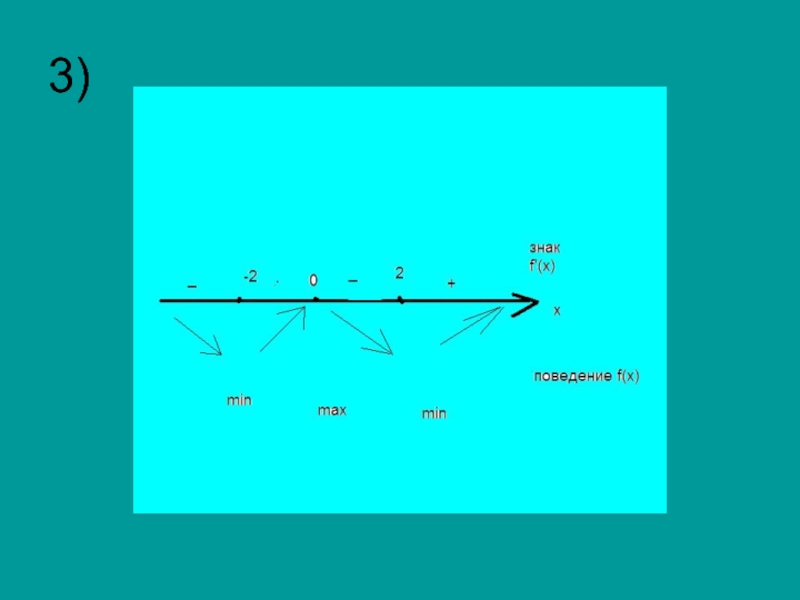
![Ответ: функция возрастает , если х Є [-2;0], [2; +∞); убывает , если хЄ(-∞;-2],[0;2].](/img/tmb/2/140947/1cf157032676824eff1f366b528a0172-800x.jpg)






