- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Готовимся к ЕГЭ.Задача С2. Угол между прямыми. презентация
Содержание
- 1. Готовимся к ЕГЭ.Задача С2. Угол между прямыми.
- 2. * Углом между двумя пересекающимися прямыми называется
- 3. * Углом между скрещивающимися прямыми называется угол
- 4. * 1) Ввести удобную систему координат.
- 5. * В кубе ABCDA1B1C1D1
- 6. * В кубе ABCDA1B1C1D1 найти угол
- 7. * В единичном кубе ABCDA1B1C1D1
- 8. * В единичном кубе ABCDA1B1C1D1 найти
- 9. 2) Длины всех ребер правильной четырехугольной пирамиды
- 10. * Тренировочные упражнения Решение Решение 4) В
- 11. B 1) В правильной
- 12. B 1) В правильной шестиугольной призме
- 13. 2) Длины всех ребер правильной
- 14. 2) Длины всех ребер правильной четырехугольной
- 15. 3) В правильной шестиугольной пирамиде SABCDEF
- 16. 3) В правильной шестиугольной пирамиде
- 17. 3) В правильной шестиугольной пирамиде SABCDEF ,
- 18. * А В С D
- 19. * А В С D Решение:
- 20. * Решение: 5) В правильной треугольной
- 21. * Решение: 5) В правильной треугольной призме
- 22. * Решение: 5) В правильной треугольной призме
- 23. * При создании презентации использовано пособие: http://www.alleng.ru/d/math/math784.htm
* Углом между двумя пересекающимися прямыми называется наименьший из углов, образованных при пересечении прямых. Определение. b а α β
Слайд 1Готовимся к ЕГЭ.
Задача С2.
Угол между прямыми.
МБОУ г. Мурманска гимназия №3
Шахова Татьяна Александровна
Слайд 2*
Углом между двумя пересекающимися прямыми называется наименьший из углов, образованных при
пересечении прямых.
Определение.
b
а
α
β
Слайд 3*
Углом между скрещивающимися прямыми называется угол между пересекающимися прямыми, соответственно параллельными
данным скрещивающимся.
Поэтапно – вычислительный метод.
b
Пример
а
α
Построить угол с сонаправленными
сторонами.
Вычислить его величину как
элемент треугольника, если удается удается включить
его в некоторый треугольник в качестве одного из его углов.
Слайд 4*
1) Ввести удобную систему координат.
Векторно - координатный метод.
Пример
2) Определить координаты
точек А, В, С, D принадлежащим прямым.
3) Определить координаты направляющих векторов
http://le-savchen.ucoz.ru/load/4-1-0-196)
4) Косинус соответствующего угла можно определить по формуле:
А
В
С
D
Назад
http://ta-shah.ucoz.ru/load/egeh/egeh_s2/koordinatnyj_metod_kljuchevye_zadachi/14-1-0-73
Слайд 5
*
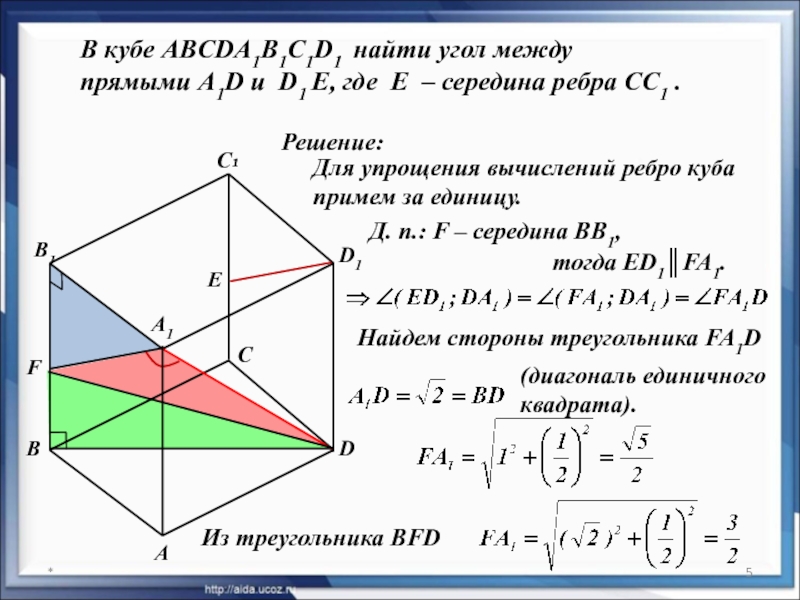
В кубе ABCDA1B1C1D1 найти угол между
прямыми A1D и D1 E,
где E – середина ребра CC1 .
А
С₁
D
D1
В1
F
В
Д. п.: F – середина ВВ1,
Решение:
(диагональ единичного
квадрата).
А1
С
E
Для упрощения вычислений ребро куба примем за единицу.
тогда ED1║FA1.
Из треугольника BFD
Найдем стороны треугольника FA1D
Слайд 6
*
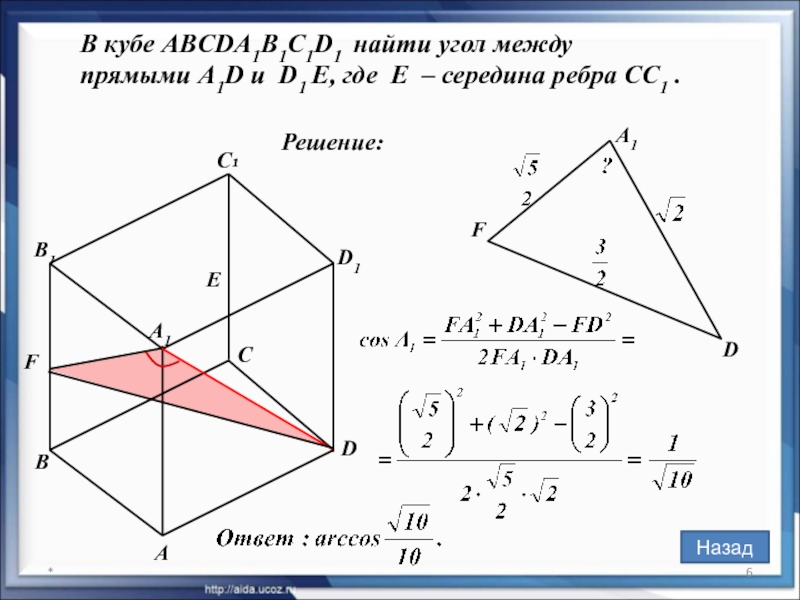
В кубе ABCDA1B1C1D1 найти угол между
прямыми A1D и D1 E,
где E – середина ребра CC1 .
А
С₁
D
D1
В1
F
В
Решение:
А1
С
E
D
F
А1
Назад
Слайд 7
*
В единичном кубе ABCDA1B1C1D1 найти угол между
прямыми АЕ и
DF, где Е и F – точки, распо-ложенные на рёбрах CD и D1C1 так, что DE=1/3DC, C1F=1/3C1C.
А
С₁
D
D1
В1
F
В
Решение:
А1
С
E
Введем прямоугольную систему
координат
Тогда:
Слайд 8*
В единичном кубе ABCDA1B1C1D1 найти угол между
прямыми АЕ и
DF, где Е и F – точки, распо-ложенные на рёбрах CD и D1C1 так, что DE=1/3DC, C1F=1/3C1C.
А
С₁
D
D1
В1
F
В
Решение:
А1
С
E
Назад
?
Слайд 92) Длины всех ребер правильной четырехугольной пирамиды PABCD равны между собой.
Найдите угол между прямыми РН и ВМ, если отрезок РН — высота данной пирамиды, точка М — середина ее бокового ребра АР.
*
Тренировочные упражнения
Решение
Решение
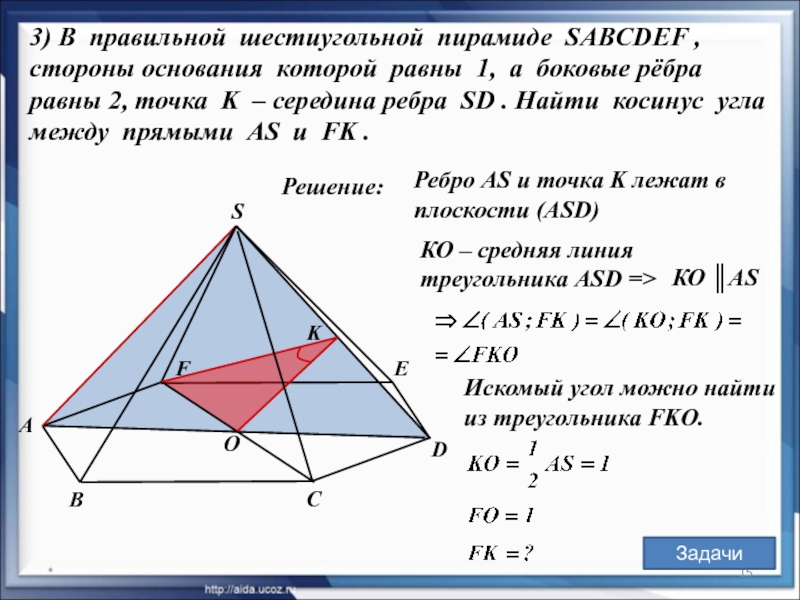
3) В правильной шестиугольной пирамиде SABCDEF , стороны основания которой равны 1, а боковые рёбра равны 2, точка K – середина ребра SD . Найти косинус угла между прямыми AS и FK .
Решение
Найти расстояние между непересекающимися
диагоналями двух смежных граней куба, длина ребра
которого равна 1 .
Слайд 10*
Тренировочные упражнения
Решение
Решение
4) В правильной треугольной призме ABCA1B1C1 , ребро
основания равно 1,
боковое ребро равно 2. Найти угол между
прямыми AС1 и B1C (поэтапно – вычислительный метод).
прямыми AС1 и B1C (поэтапно – вычислительный метод).
5) В правильной треугольной призме ABCA1B1C1 , ребро
основания равно 1, боковое ребро равно 2. Найти угол между
прямыми AС1 и B1C (векторно - координатный метод).
Слайд 11
B
1) В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все ребра которой равны 1,
найти косинус угла между D1E и DB1.
Титова Мария
A
A1
B1
C
C1
D1
D
E
F1
F
E1
DB найдем из треугольника DCB
D1E║AB1
Решение:
(большая диагональ правильного шестиугольника).
DB1 найдем из треугольника DB1B
Задачи
Найдем стороны треугольника FA1D
Слайд 12
B
1) В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1, все ребра которой равны 1,
найти косинус угла между D1E и DB1.
Титова Мария
A
A1
B1
C
C1
D1
D
E
F1
F
E1
Решение:
Рассмотрим треугольник DB1A
A
D
B1
Задачи
Слайд 13
2) Длины всех ребер правильной четырехугольной пирамиды PABCD равны между собой.
Найдите угол между прямыми РН и ВМ, если отрезок РН — высота данной пирамиды, точка М — середина ее бокового ребра АР.
Тюрина Анастасия
Решение:
Для упрощения вычислений ребро пирамиды примем за единицу.
Искомый угол можно найти из прямоугольного треугольника MNB.
Для этого найдем две его стороны.
В треугольнике APH АН=
Задачи
Слайд 14
2) Длины всех ребер правильной четырехугольной пирамиды PABCD равны между собой.
Найдите угол между прямыми РН и ВМ, если отрезок РН — высота данной пирамиды, точка М — середина ее бокового ребра АР.
Тюрина Анастасия
Решение:
В равностороннем треугольнике MPB:
Рассмотрим треугольник MNB
Задачи
Слайд 15
3) В правильной шестиугольной пирамиде SABCDEF , стороны основания которой равны
1, а боковые рёбра равны 2, точка K – середина ребра SD . Найти косинус угла между прямыми AS и FK .
*
А
В
С
D
Е
F
S
K
Решение:
Ребро АS и точка K лежат в
плоскости (ASD)
O
КО – средняя линия треугольника ASD =>
КО ║AS
Искомый угол можно найти
из треугольника FKO.
Задачи
Слайд 16
3) В правильной шестиугольной пирамиде SABCDEF , стороны основания которой равны
1, а боковые рёбра равны 2, точка K – середина ребра SD . Найти косинус угла между прямыми AS и FK .
*
А
В
С
D
Е
F
S
K
Решение:
O
Из треугольника FED
FK – медиана
треугольника FSD =>
Задачи
Слайд 173) В правильной шестиугольной пирамиде SABCDEF , стороны основания которой равны
1, а боковые рёбра равны 2, точка K – середина ребра SD . Найти косинус угла между прямыми AS и FK .
*
А
В
С
D
Е
F
S
K
Решение:
O
Из треугольника FKO
Задачи
Слайд 18
*
А
В
С
D
Решение:
Д. п.:
4) В правильной треугольной призме ABCA1B1C1 , ребро
основания равно
1, боковое ребро равно 2. Найти угол между
прямыми AС1 и B1C (поэтапно – вычислительный метод).
прямыми AС1 и B1C (поэтапно – вычислительный метод).
А1
С1
В1
D1
CD1║AC1
Искомый угол можно найти
из треугольника CB1D1.
Из треугольника CC1D1:
Из треугольника B1C1D1:
Задачи
Слайд 19
*
А
В
С
D
Решение:
4) В правильной треугольной призме ABCA1B1C1 , ребро
основания равно 1, боковое
ребро равно 2. Найти угол между
прямыми AС1 и B1C (поэтапно – вычислительный метод).
прямыми AС1 и B1C (поэтапно – вычислительный метод).
А1
С1
В1
D1
В треугольнике CB1D1:
Задачи
Слайд 20
*
Решение:
5) В правильной треугольной призме ABCA1B1C1 , ребро
основания равно 1, боковое
ребро равно 2. Найти угол между
прямыми AС1 и B1C (векторно - координатный метод).
прямыми AС1 и B1C (векторно - координатный метод).
А
В
С
А1
С1
В1
Введем прямоугольную систему
координат
Тогда:
X
Z
Y
А
X
Y
В
С
H
Задачи
Слайд 21*
Решение:
5) В правильной треугольной призме ABCA1B1C1 , ребро
основания равно 1, боковое
ребро равно 2. Найти угол между
прямыми AС1 и B1C (векторно - координатный метод).
прямыми AС1 и B1C (векторно - координатный метод).
Задачи
А
В
С
А1
С1
В1
Тогда:
X
Z
Y
Слайд 22*
Решение:
5) В правильной треугольной призме ABCA1B1C1 , ребро
основания равно 1, боковое
ребро равно 2. Найти угол между
прямыми AС1 и B1C (векторно - координатный метод).
прямыми AС1 и B1C (векторно - координатный метод).
Задачи
?
