- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Геометрія9 клас презентация
Содержание
- 1. Геометрія9 клас
- 2. Тема уроку: ТЕОРЕМА СИНУСІВ На уроці: Узагальнююче повторення Теорема синусів Тренувальні вправи
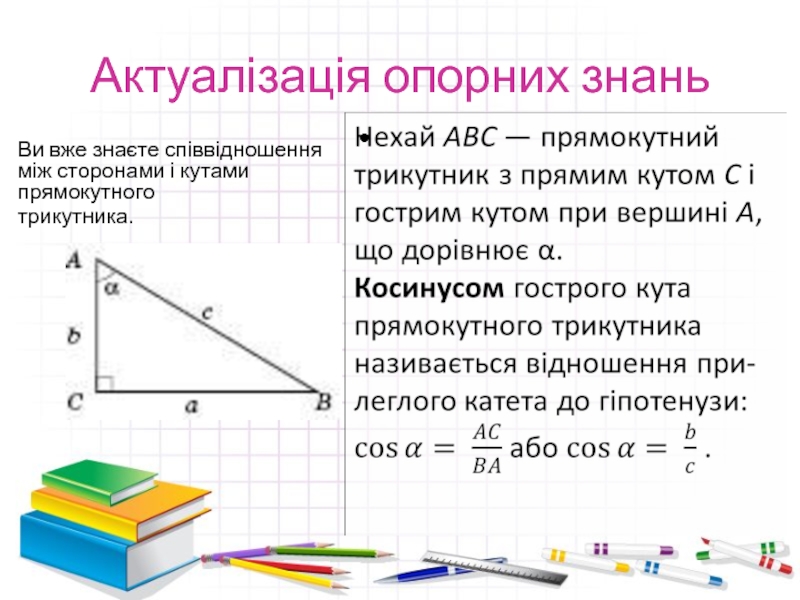
- 3. Актуалізація опорних знань Ви вже знаєте співвідношення між сторонами і кутами прямокутного трикутника.
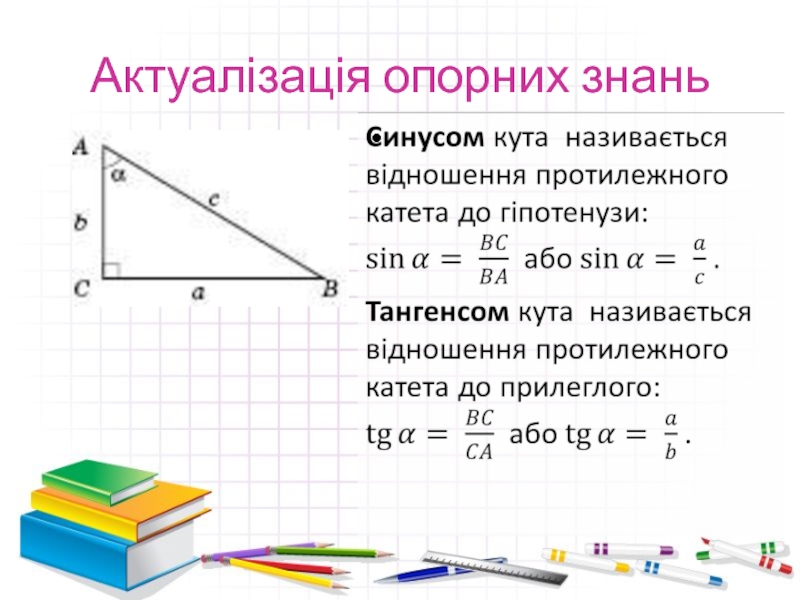
- 4. Актуалізація опорних знань
- 5. Співвідношення між сторонами і кутами довільного трикутника
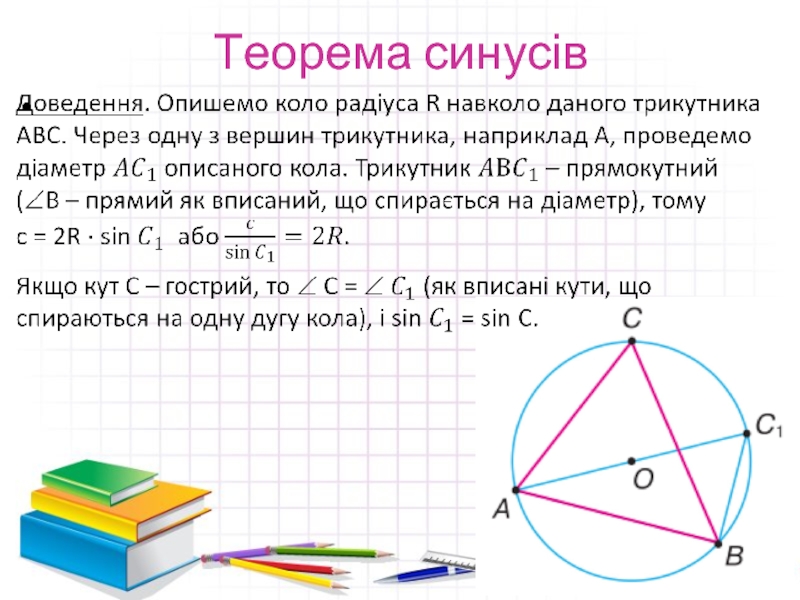
- 6. Теорема синусів
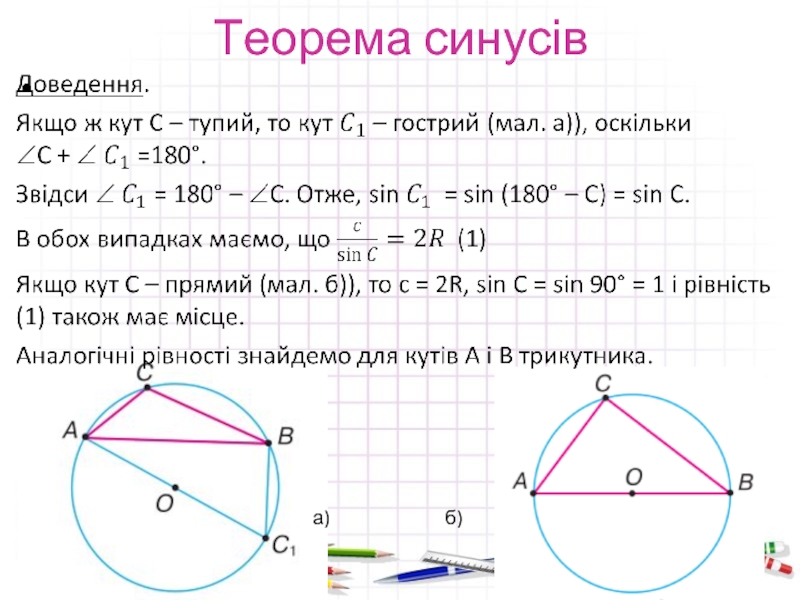
- 7. Теорема синусів а) б)
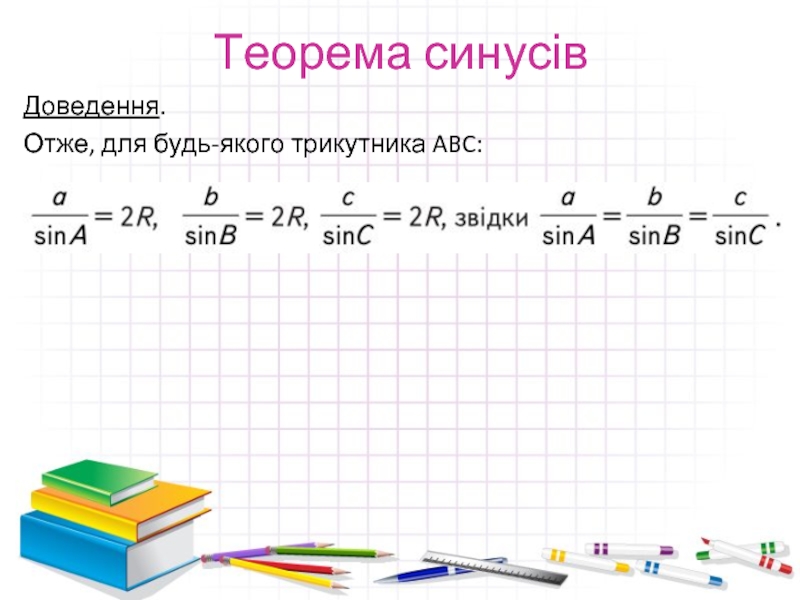
- 8. Теорема синусів Доведення. Отже, для будь-якого трикутника ABC:
- 9. Наслідки з теореми синусів Наслідок 1. У
- 10. Наслідки з теореми синусів Наслідок 2. У
- 11. Первинне застосування набутих знань Робота з підручником (ст. 19)
- 12. Первинне застосування набутих знань Робота з підручником (ст. 19)
- 13. До уваги! Теорема синусів дає можливість за
- 14. Усні вправи
- 15. Напівусні вправи 63'. За даними на малюнку
- 16. Колективне виконання вправ
- 17. Коментоване виконання опорних вправ 73°. Дві сторони
- 18. Коментоване виконання опорних вправ
- 19. Домашнє завдання Опрацювати п. 3 Виконати вправи № 66, 67, 68(3), 69(3), 77
Тема уроку:
ТЕОРЕМА СИНУСІВ На уроці: Узагальнююче повторення Теорема синусів Тренувальні вправи
Слайд 3Актуалізація опорних знань
Ви вже знаєте співвідношення між сторонами і кутами прямокутного
трикутника.
Слайд 5Співвідношення між сторонами і кутами довільного трикутника
Позначатимемо сторони трикутника через a,
b, c, а протилежні їм кути – через α, β, γ або ∠A, ∠ B, ∠ C.
Теорема синусів.
Сторони трикутника
пропорційні синусам протилежних кутів.
Слайд 9Наслідки з теореми синусів
Наслідок 1. У будь-якому трикутнику відношення сторони до
синуса протилежного кута дорівнює діаметру кола, описаного навколо цього трикутника:
Чи можна знайти сторону трикутника за радіусом R описаного кола і кутом, що лежить проти цієї сторони? Так. За наслідком 1 з теореми синусів.
Чи можна знайти сторону трикутника за радіусом R описаного кола і кутом, що лежить проти цієї сторони? Так. За наслідком 1 з теореми синусів.
Слайд 10Наслідки з теореми синусів
Наслідок 2. У трикутнику проти більшої сторони лежить
більший кут, проти більшого кута лежить більша сторона.
(Спробуйте вдома довести, розглянувши гострокутний і тупокутний трикутники.)
(Спробуйте вдома довести, розглянувши гострокутний і тупокутний трикутники.)
Слайд 13До уваги!
Теорема синусів дає можливість за стороною і прилеглими до неї
кутами або за двома сторонами і кутом, протилежним одній з них, знаходити інші сторони і кути трикутника.
Слайд 15Напівусні вправи
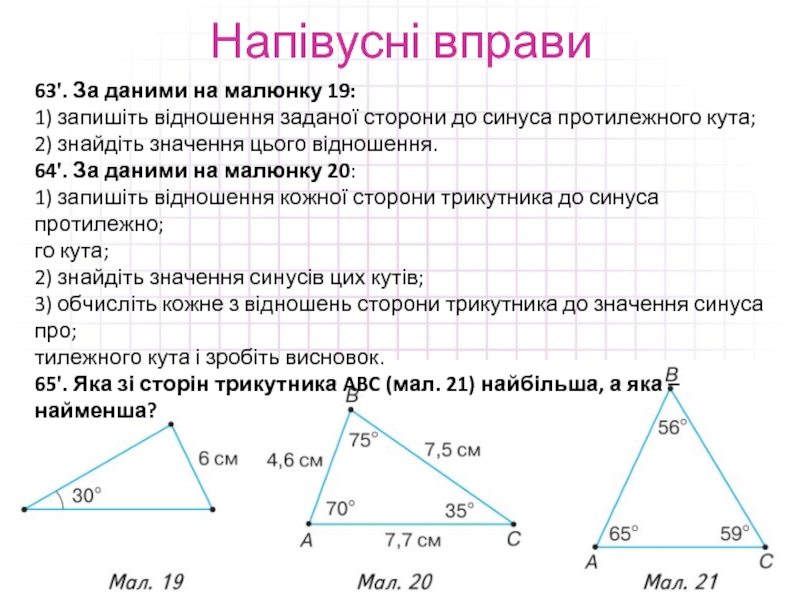
63'. За даними на малюнку 19:
1) запишіть відношення заданої сторони
до синуса протилежного кута;
2) знайдіть значення цього відношення.
64'. За даними на малюнку 20:
1) запишіть відношення кожної сторони трикутника до синуса протилежно;
го кута;
2) знайдіть значення синусів цих кутів;
3) обчисліть кожне з відношень сторони трикутника до значення синуса про;
тилежного кута і зробіть висновок.
65'. Яка зі сторін трикутника ABC (мал. 21) найбільша, а яка – найменша?
2) знайдіть значення цього відношення.
64'. За даними на малюнку 20:
1) запишіть відношення кожної сторони трикутника до синуса протилежно;
го кута;
2) знайдіть значення синусів цих кутів;
3) обчисліть кожне з відношень сторони трикутника до значення синуса про;
тилежного кута і зробіть висновок.
65'. Яка зі сторін трикутника ABC (мал. 21) найбільша, а яка – найменша?
Слайд 17Коментоване виконання опорних вправ
73°. Дві сторони трикутника дорівнюють 7 см і
9 см. Чи може кут, протилежний стороні 7 см, бути: 1) тупим; 2) гострим; 3) прямим?
74°. Сторони трикутника дорівнюють 4 см, 5 см, 6 см. Чи може кут, протилежний стороні 4 см, бути: 1) більшим за 60°; 2) рівним 60°; 3) меншим від 60°?
75°. BC – найменша сторона трикутника ABC. Чи може кут A дорівнювати: 1) 61°; 2) 60°; 3) 59°?
74°. Сторони трикутника дорівнюють 4 см, 5 см, 6 см. Чи може кут, протилежний стороні 4 см, бути: 1) більшим за 60°; 2) рівним 60°; 3) меншим від 60°?
75°. BC – найменша сторона трикутника ABC. Чи може кут A дорівнювати: 1) 61°; 2) 60°; 3) 59°?
