математики
МОУ «Гимназия №3»,
г. Чистополь, РТ
- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Функционально-графический подход к решению задач с параметром и модулем презентация
Содержание
- 1. Функционально-графический подход к решению задач с параметром и модулем
- 2. Цели урока: повторение названий элементарных функций и
- 3. План конференции Повторение (разминка). Практическая работа. Графики
- 4. Функции и их графики
- 5. Линейная функция y = kx + b График - прямая
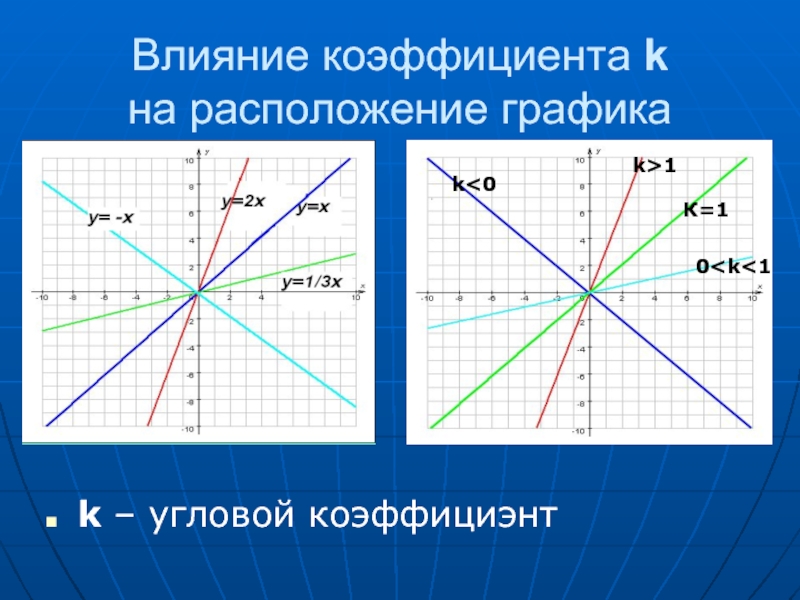
- 6. Влияние коэффициента k на расположение графика k – угловой коэффициэнт К=1 k>1 0
- 7. у =ах2+bх+с Квадратичная функция График - парабола
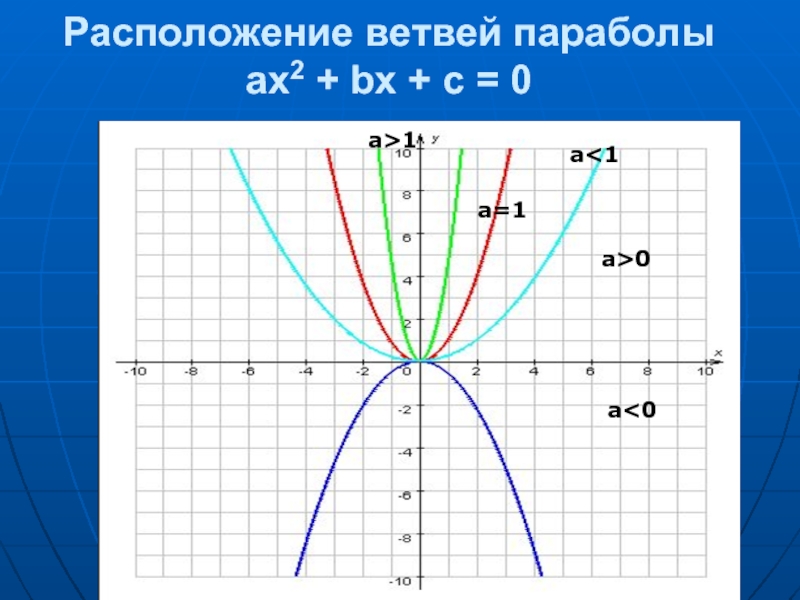
- 8. Расположение ветвей параболы ах2 + bх + с = 0 a1 а=1 a>0 a
- 9. Смещение параболы относительно начала координат У=ах2+n У=а(х-m)2
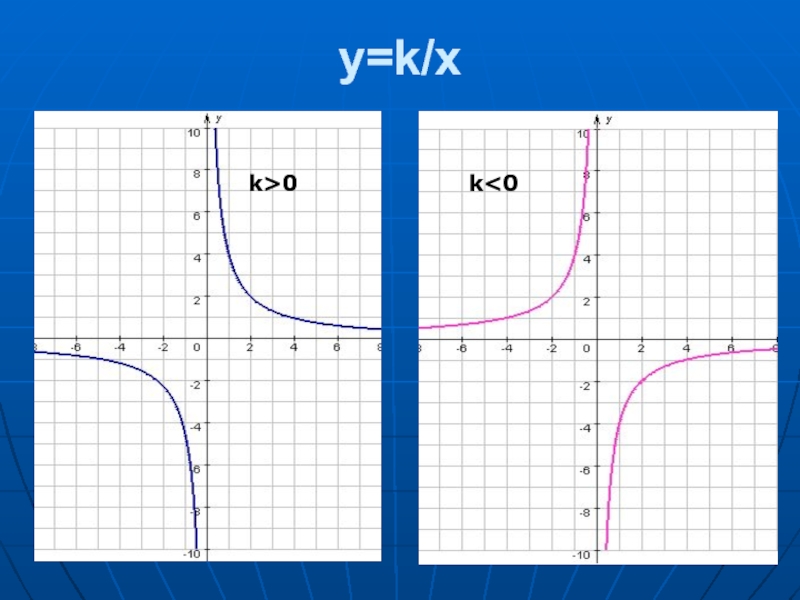
- 10. y=k/x k>0 k
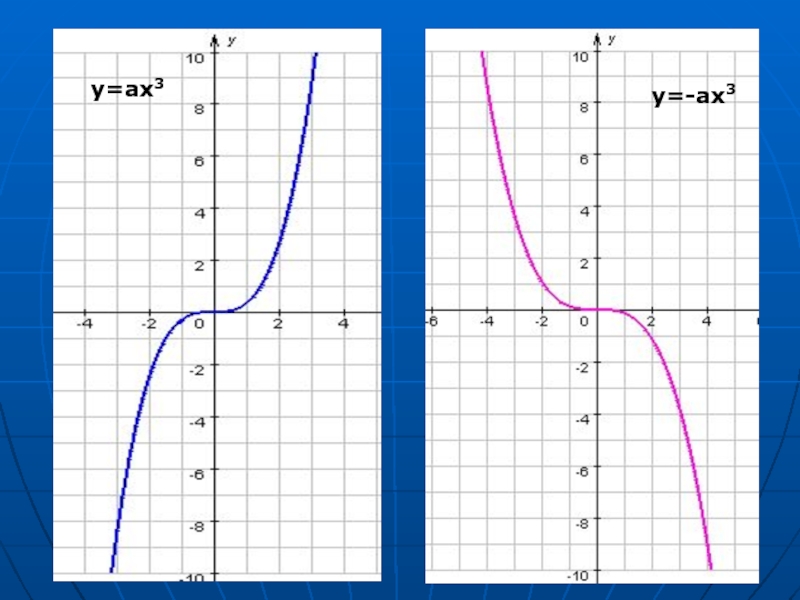
- 12. y=ах3 y=-ах3
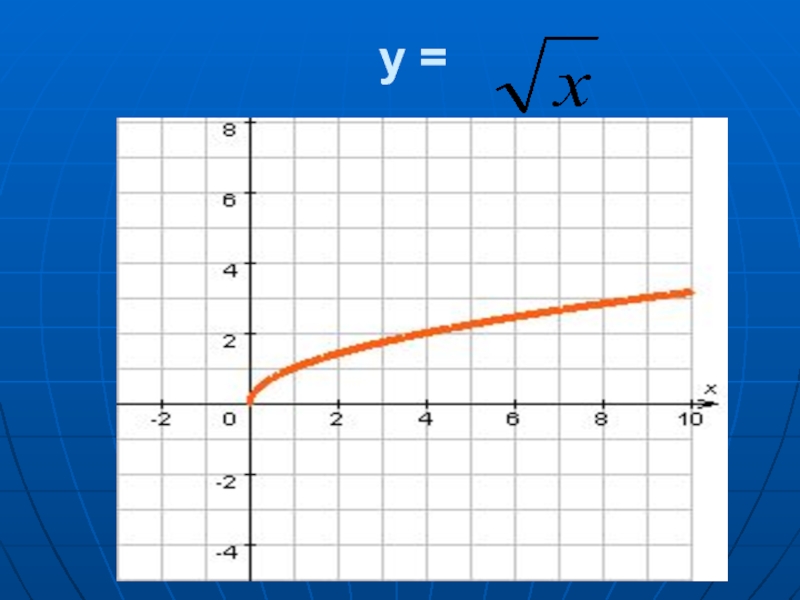
- 13. y =
- 14. Уравнение окружности. (Х-Х0)2+(У-У0)2=R2 Х0 ;
- 15. Кроссворд «Функции и графики»
- 16. ? ? ? ? ? ? ?
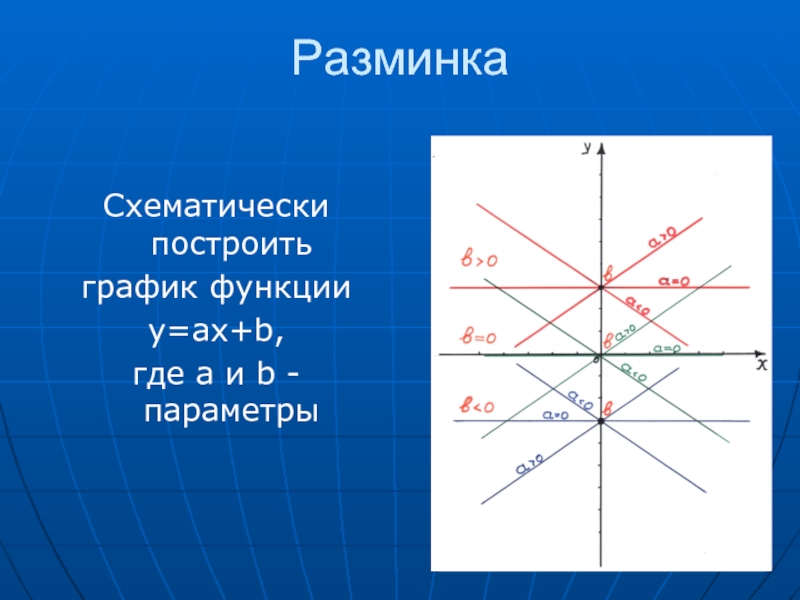
- 17. Разминка Схематически построить график функции
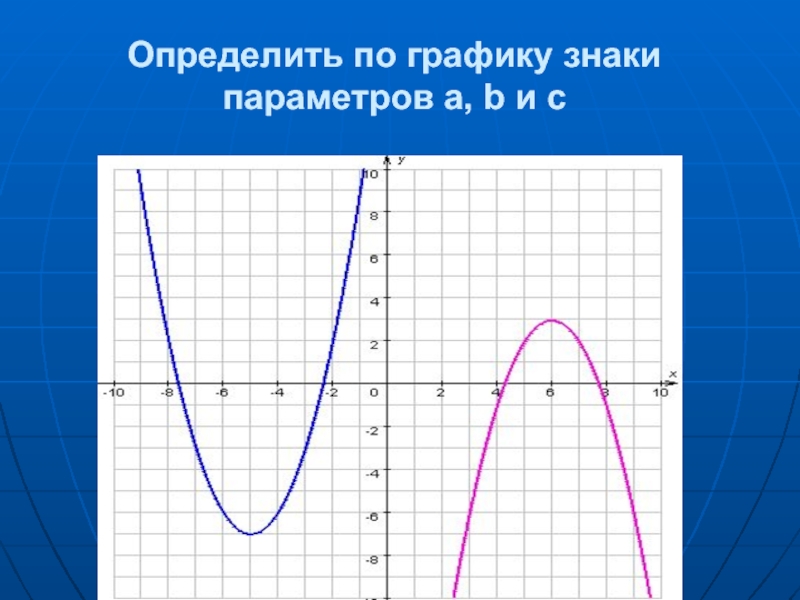
- 18. Определить по графику знаки параметров a, b и c
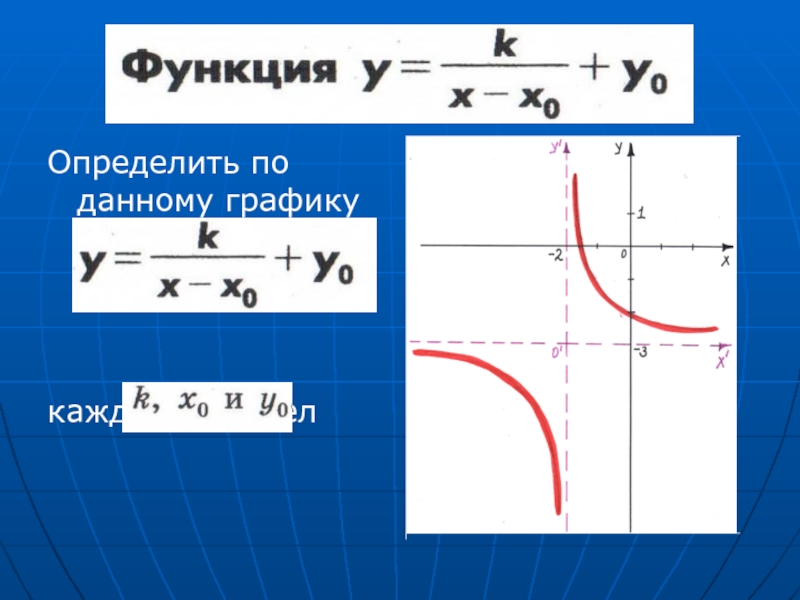
- 19. Определить по данному графику функции
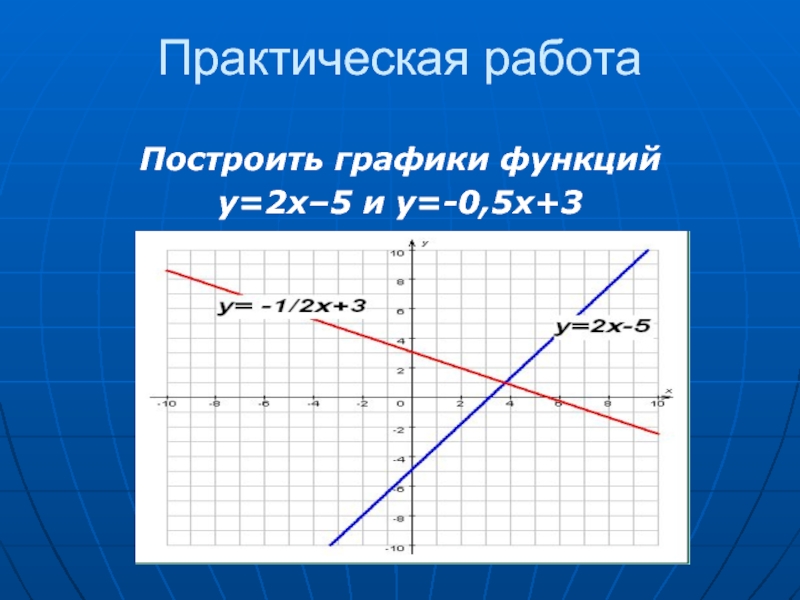
- 20. Практическая работа Построить графики функций y=2x–5 и y=-0,5x+3
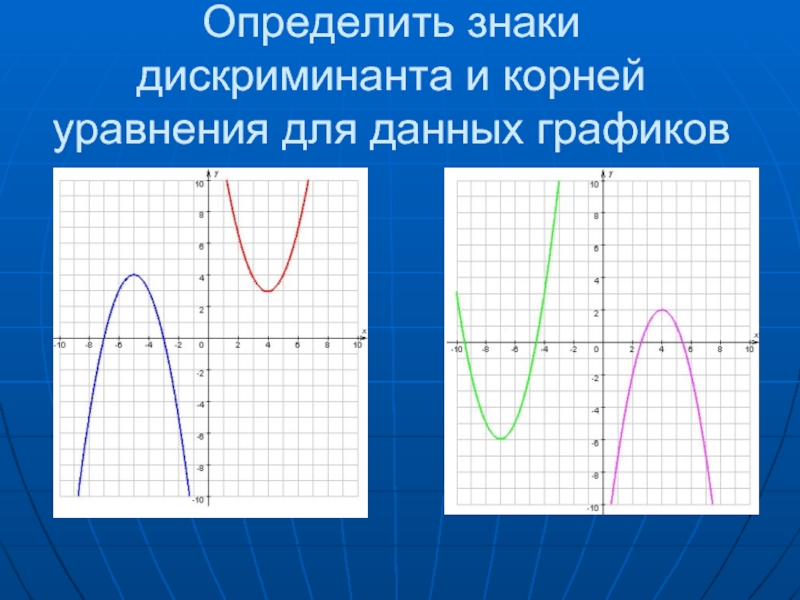
- 21. Определить знаки дискриминанта и корней уравнения для данных графиков
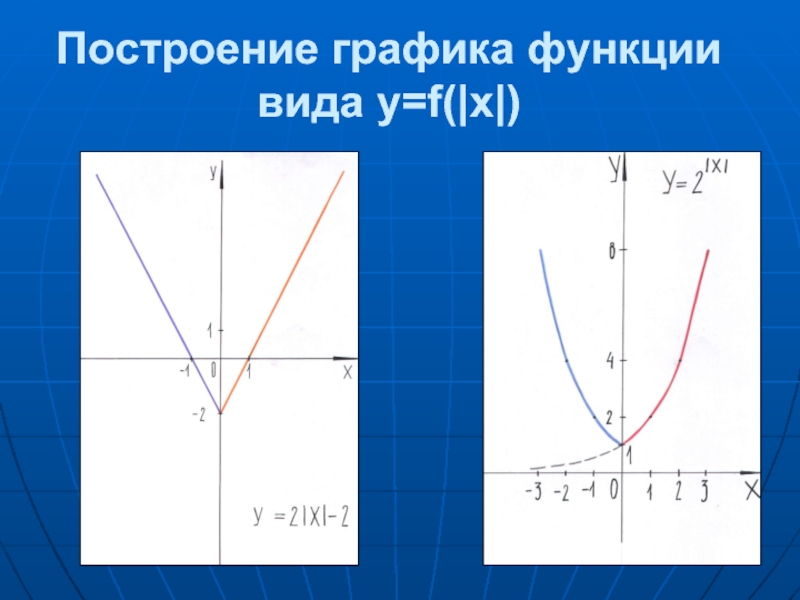
- 22. Мини-проекты 1.1. Построение графика функции вида y=f(|x|)
- 23. l а l={
- 24. Построение графика функции вида y=f(|x|)
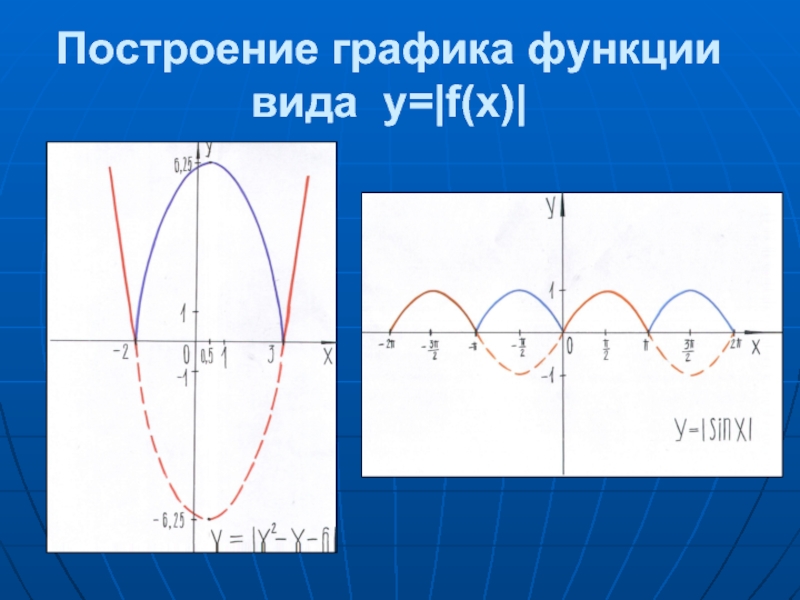
- 25. Построение графика функции вида у=|f(x)|
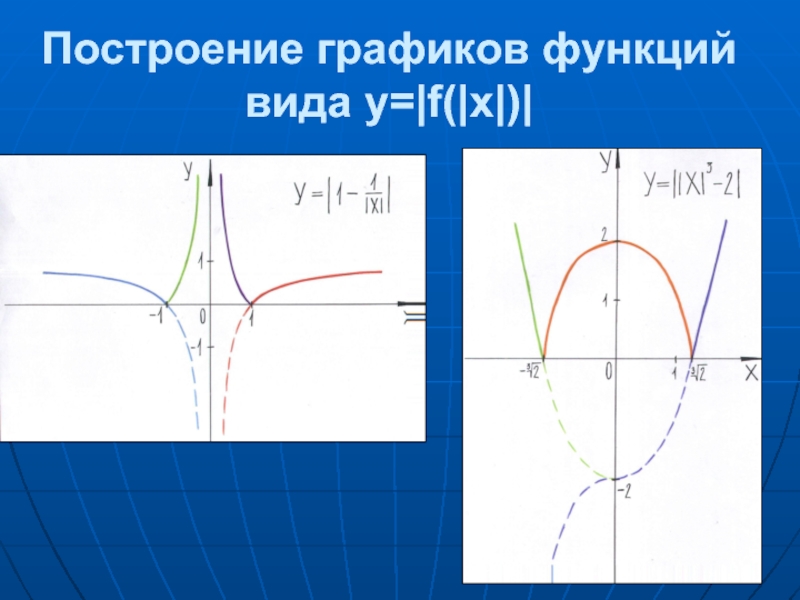
- 26. Построение графиков функций вида y=|f(|x|)|
- 27. Решение задач Уравнение, содержащее модуль Решить уравнение Ix-3I=3x+7
- 28. Решение задач Решить уравнение с параметром При
- 29. Решение уравнения с параметром 4 Ix-aI
- 30. Область значений функции При каком
- 31. Найти область значения функции у = √ 9 - х². Область значений функции
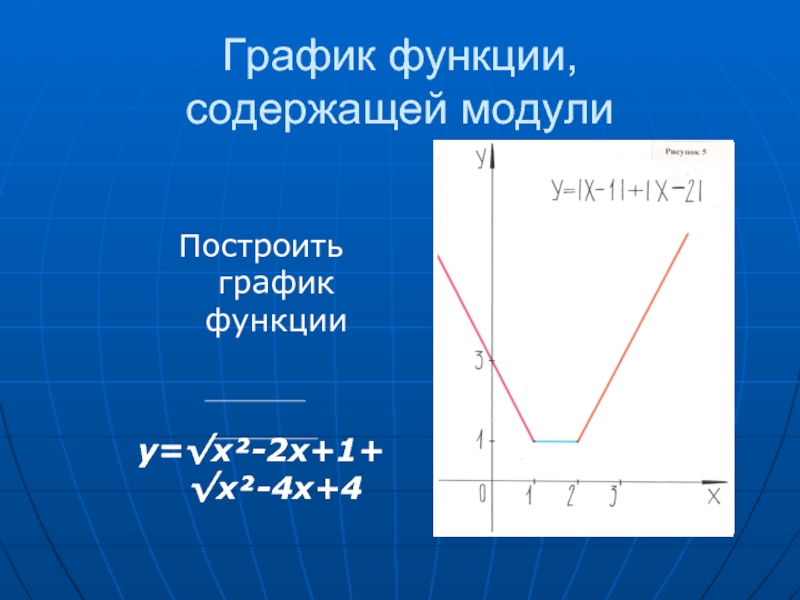
- 32. График функции, содержащей модули Построить график функции y=√x²-2x+1+ √x²-4x+4
- 33. Решение задачи с параметром графическим способом. Задача
- 34. Практическая работа «Рисуем по координатам» 1)
- 35. Рисуем по координатам
Цели урока: повторение названий элементарных функций и их графики; повторение их расположений по координатным четвертям; применение графиков функций при решении задач с модулем и параметром.
Слайд 2Цели урока:
повторение названий элементарных функций и
их графики;
повторение их расположений по
координатным четвертям;
применение графиков функций при решении задач с модулем и параметром.
применение графиков функций при решении задач с модулем и параметром.
Слайд 3План конференции
Повторение (разминка).
Практическая работа.
Графики функций, содержащие модуль и модули.
Графический способ решения
уравнений с параметром и модулем.
Слайд 9Смещение параболы относительно начала координат
У=ах2+n
У=а(х-m)2
n
-n
У=ах2+n
У=ах2
У=ах2-n
-m
m
У=а(х+m)2
У=ах2
У=а(х-m)2
Слайд 14 Уравнение окружности.
(Х-Х0)2+(У-У0)2=R2
Х0 ; У0 – координаты
центра окружности
R – радиус окружности
R – радиус окружности
Слайд 16?
?
?
?
?
?
?
?
Как называется график обратной пропорциональности?
Что является графиком линейной функции?
?
Как называется независимая
переменная?
Как называется равенство, содержащее неизвестное?
Значение переменной, при котором уравнение превращается в верное равенство.
Способ решения системы уравнений.
Слайд 22Мини-проекты
1.1. Построение графика функции вида y=f(|x|)
1.2. Построение графика функции вида у=|f(x)|
1.3.
Построение графика функции вида y=|f(|x|)|
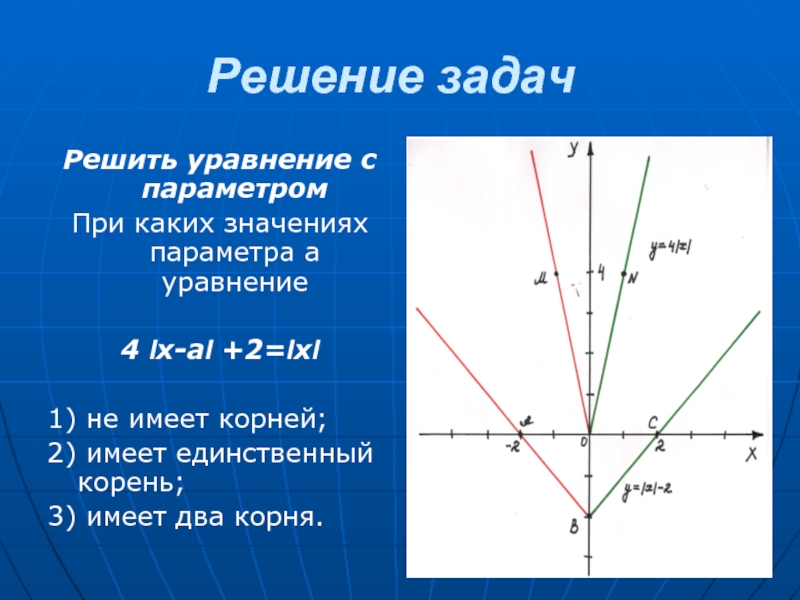
Слайд 28Решение задач
Решить уравнение с параметром
При каких значениях параметра а уравнение
4 Ix-aI
+2=IxI
1) не имеет корней;
2) имеет единственный корень;
3) имеет два корня.
1) не имеет корней;
2) имеет единственный корень;
3) имеет два корня.
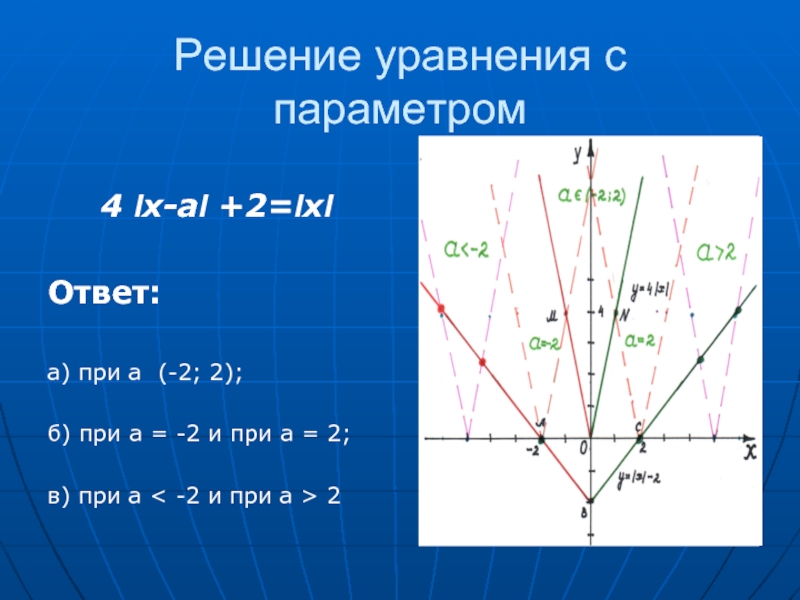
Слайд 29Решение уравнения с параметром
4 Ix-aI +2=IxI
Ответ:
а) при а (-2; 2);
б) при а = -2 и при а = 2;
в) при а < -2 и при а > 2
Слайд 30Область значений функции
При каком значении параметра а минимум функции y=3x²-2аx-4
равен максимуму
функции y=3аx²-2аx-8?
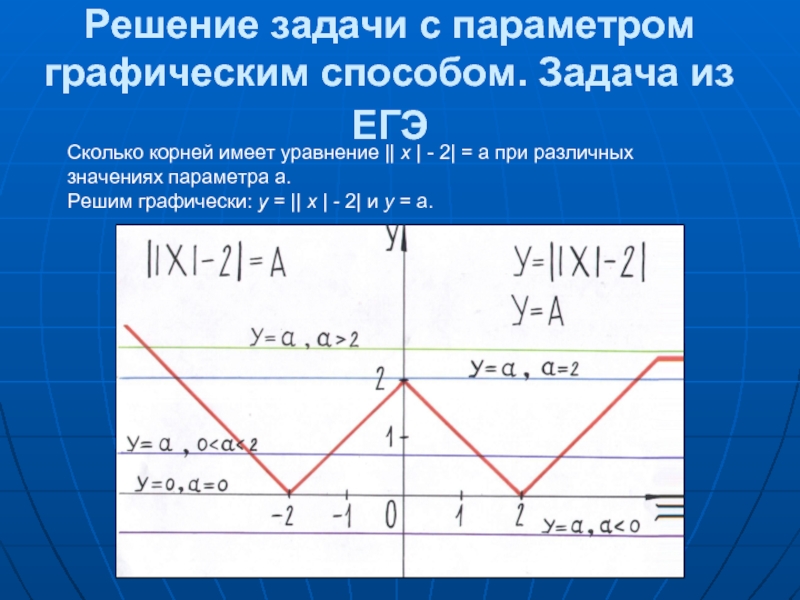
Слайд 33Решение задачи с параметром графическим способом. Задача из ЕГЭ
Сколько корней
имеет уравнение || х | - 2| = а при различных значениях параметра а.
Решим графически: у = || х | - 2| и у = а.
Решим графически: у = || х | - 2| и у = а.
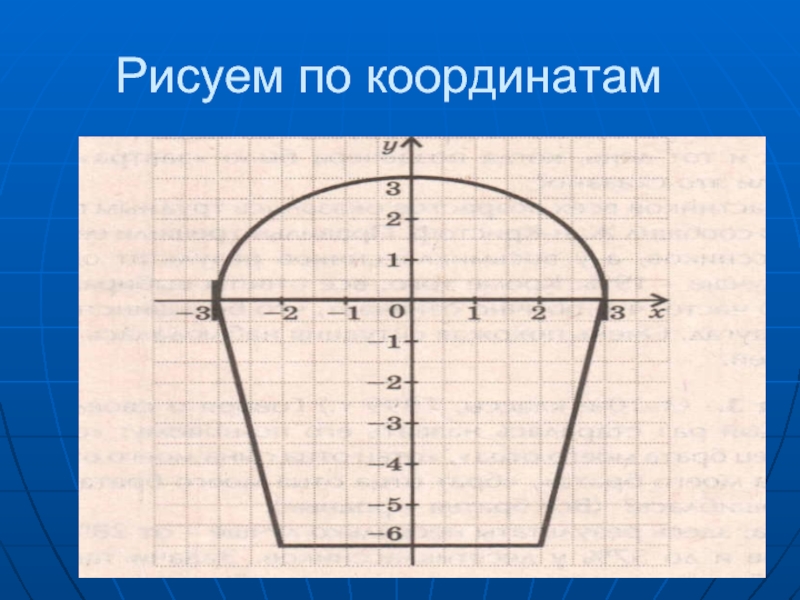
Слайд 34Практическая работа
«Рисуем по координатам»
1) IxI=3, -0,5 ≤ y ≤ 0,5;
2)
y = 0, -3 ≤ x ≤ 3;
3) y = -6, -2 ≤ x ≤ 2;
4) y = 6 IxI – 18, - 6 ≤ y ≤ 0;
5) x² + y² = 9, 0 ≤ y ≤ 3.
3) y = -6, -2 ≤ x ≤ 2;
4) y = 6 IxI – 18, - 6 ≤ y ≤ 0;
5) x² + y² = 9, 0 ≤ y ≤ 3.
