- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Функции их графики и свойства презентация
Содержание
- 1. Функции их графики и свойства
- 2. Линейная функция Линейной функцией называется функция, которую
- 3. Расположение графика в зависимости от чисел k
- 4. Расположение графика в зависимости от чисел k и b k>0, то функция возрастает. k
- 5. Прямая пропорциональность Линейную функцию, задаваемою формулой у
- 6. Обратная пропорциональность Функция, которую можно задать формулой
- 7. При к>0 график расположен в первой и
- 8. Функция у = х² и у =
- 9. Функция у = kх²
- 10. Функция у = х³ Область определения –
- 11. Функция у = |х| Область определения –
- 12. Функция квадратного корня из х. Область определения
- 13. Работа 1. Вариант 1. №15.
- 14. Работа 1. Вариант 2. №15.
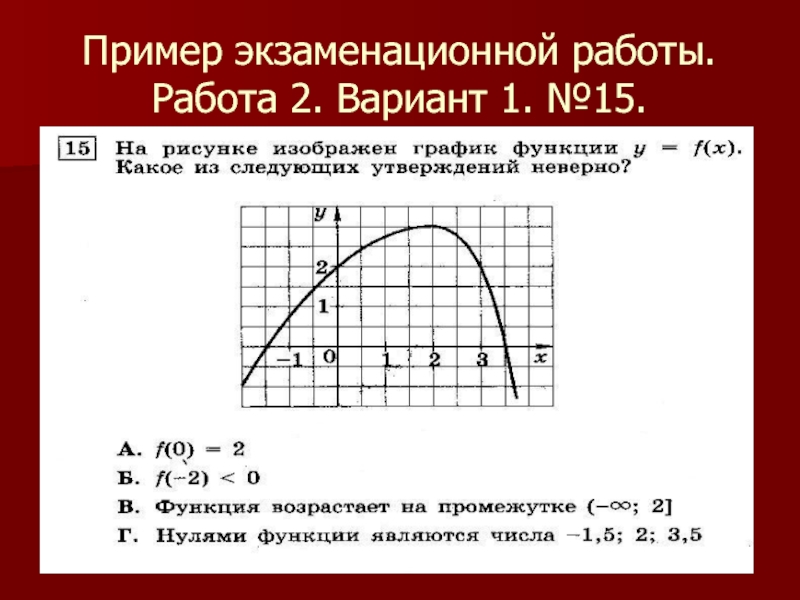
- 15. Работа 2. Вариант 1. №15.
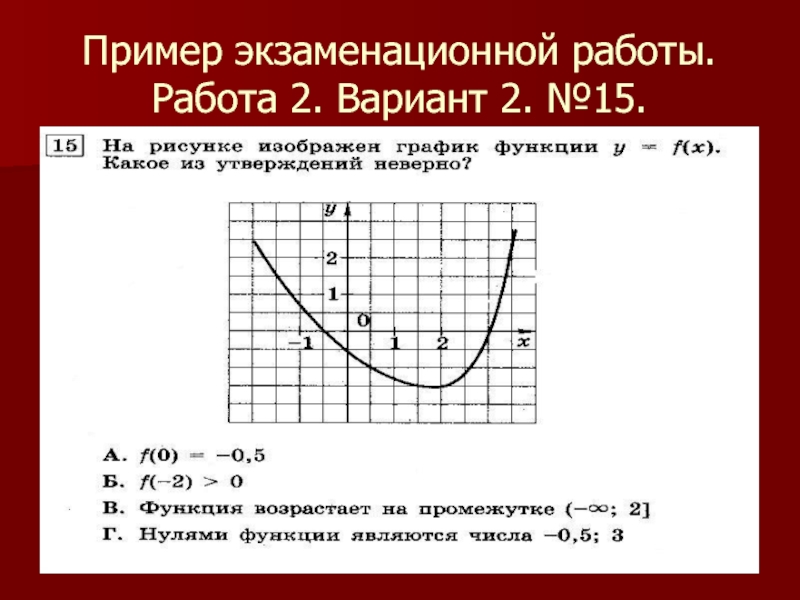
- 16. Работа 2. Вариант 2. №15.
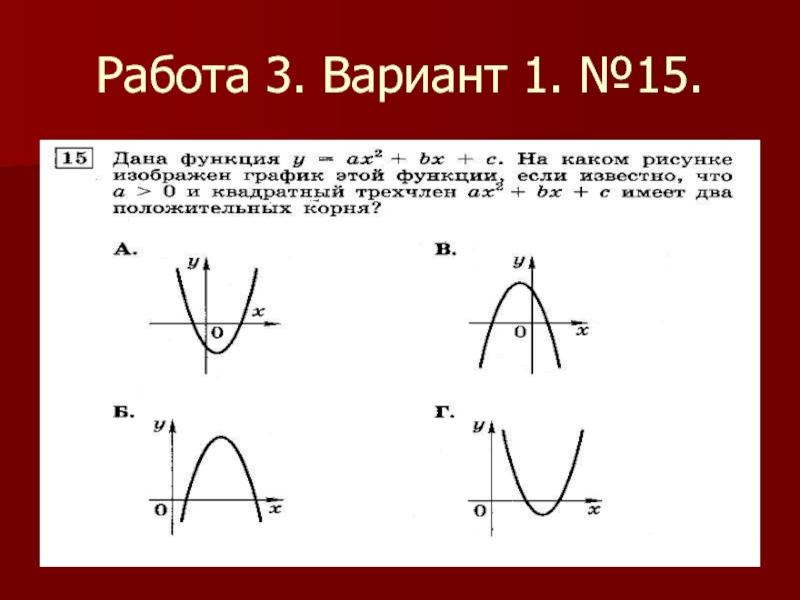
- 17. Работа 3. Вариант 1. №15.
- 18. Работа 3. Вариант 2. №15.
- 19. Работа 4. Вариант 1. №15.
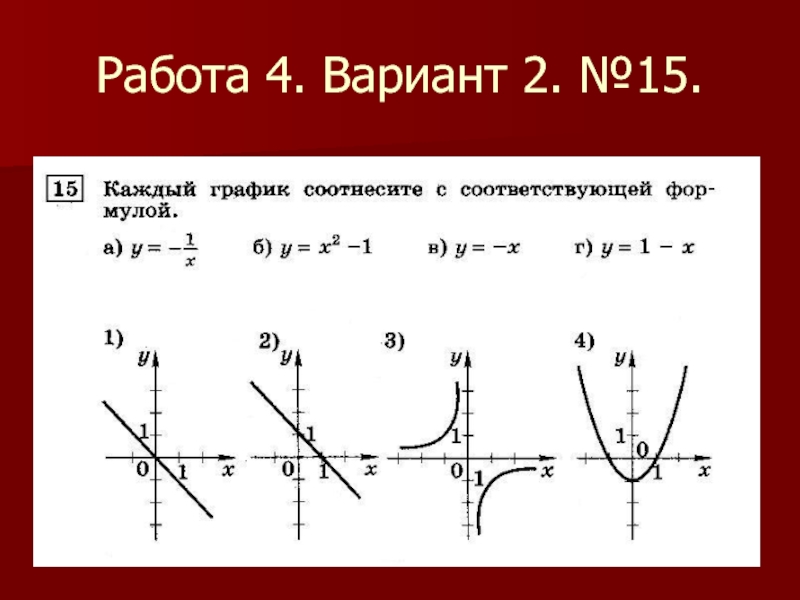
- 20. Работа 4. Вариант 2. №15.
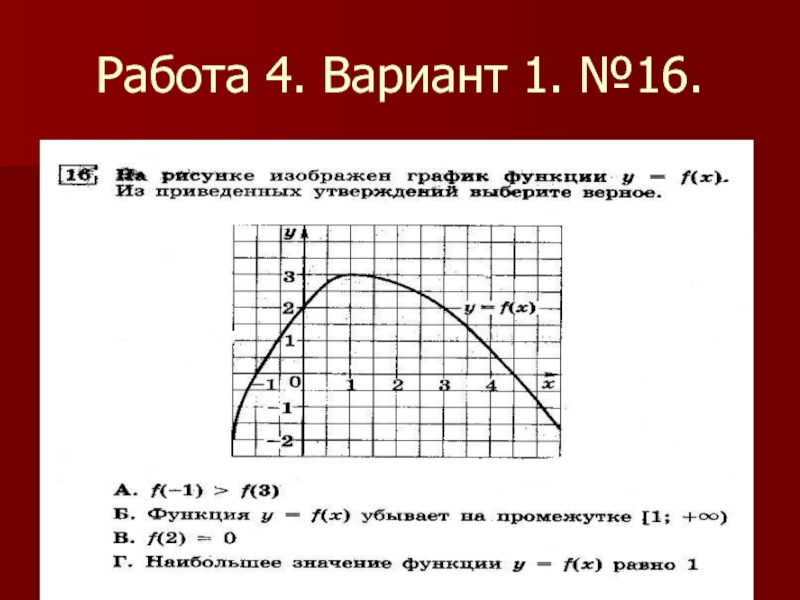
- 21. Работа 4. Вариант 1. №16.
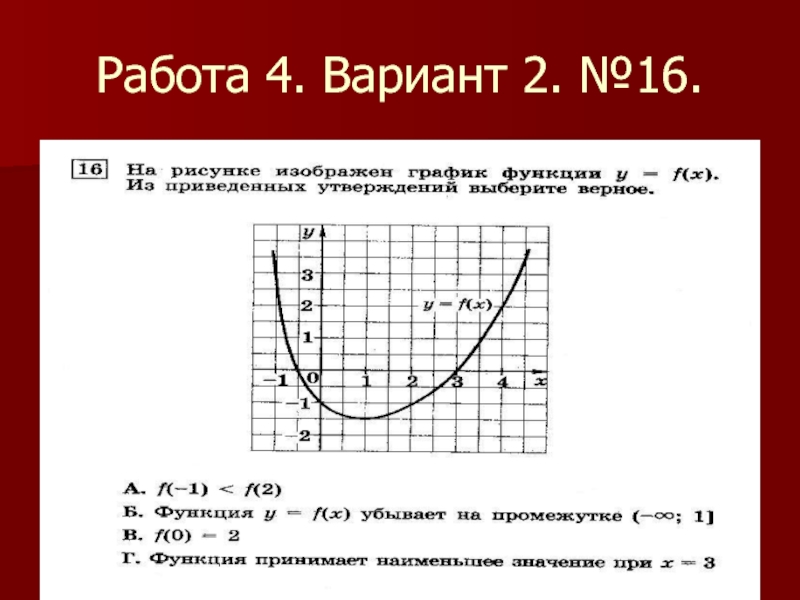
- 22. Работа 4. Вариант 2. №16.
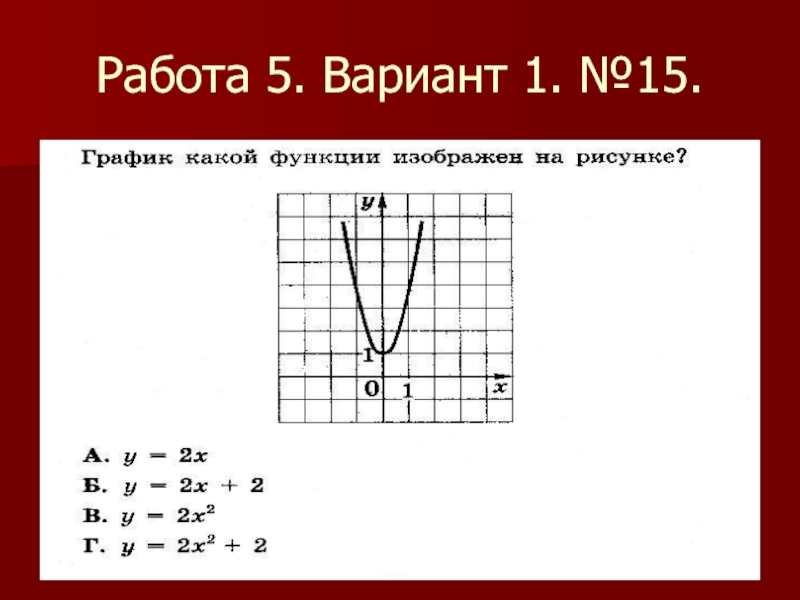
- 23. Работа 5. Вариант 1. №15.
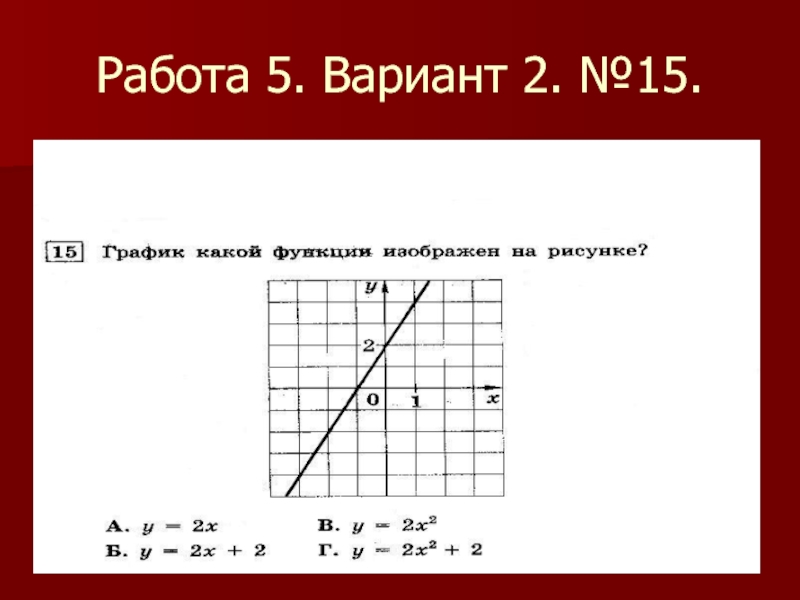
- 24. Работа 5. Вариант 2. №15.
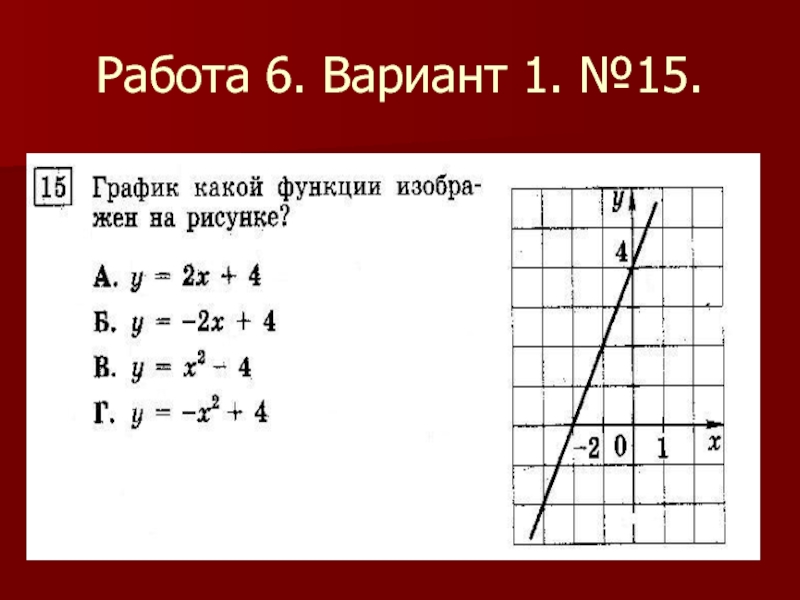
- 25. Работа 6. Вариант 1. №15.
- 26. Работа 6. Вариант 2. №15.
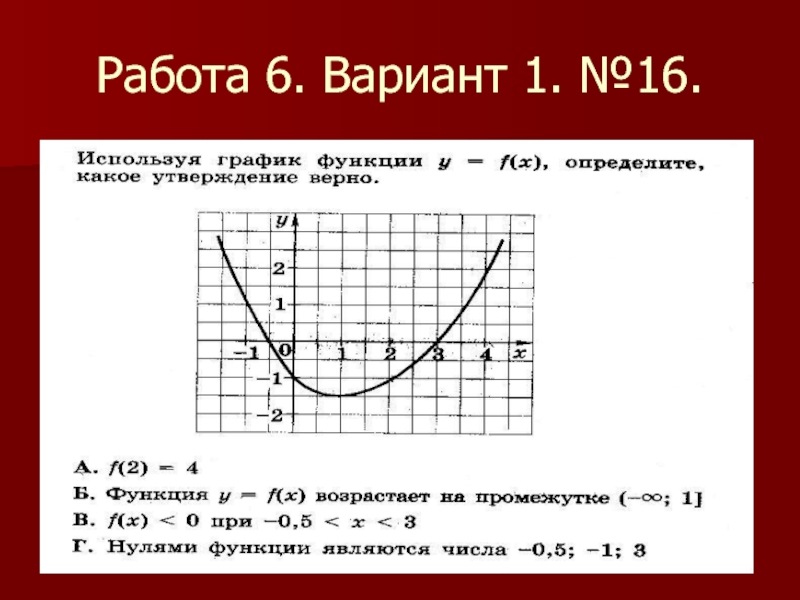
- 27. Работа 6. Вариант 1. №16.
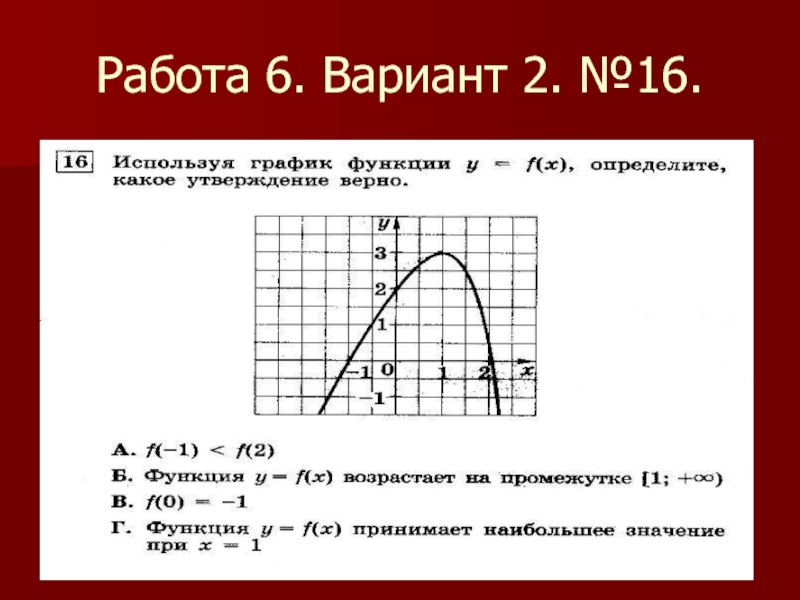
- 28. Работа 6. Вариант 2. №16.
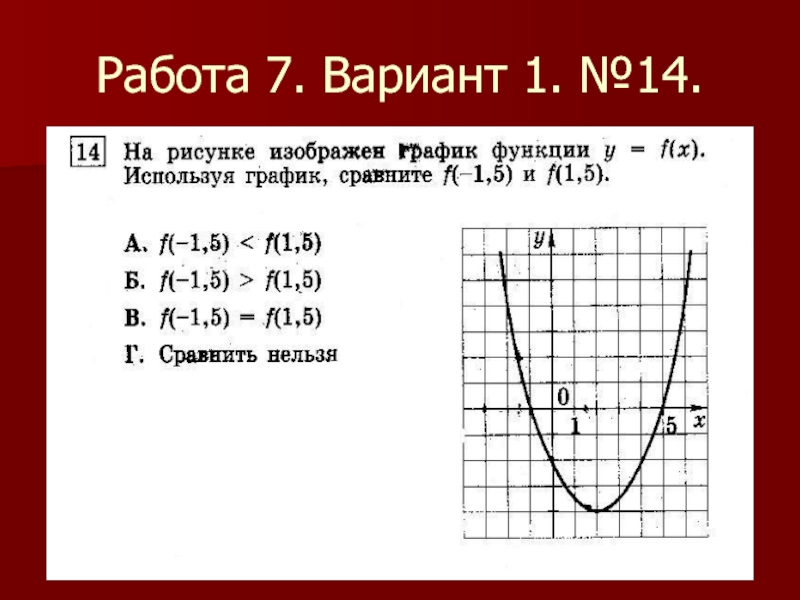
- 29. Работа 7. Вариант 1. №14.
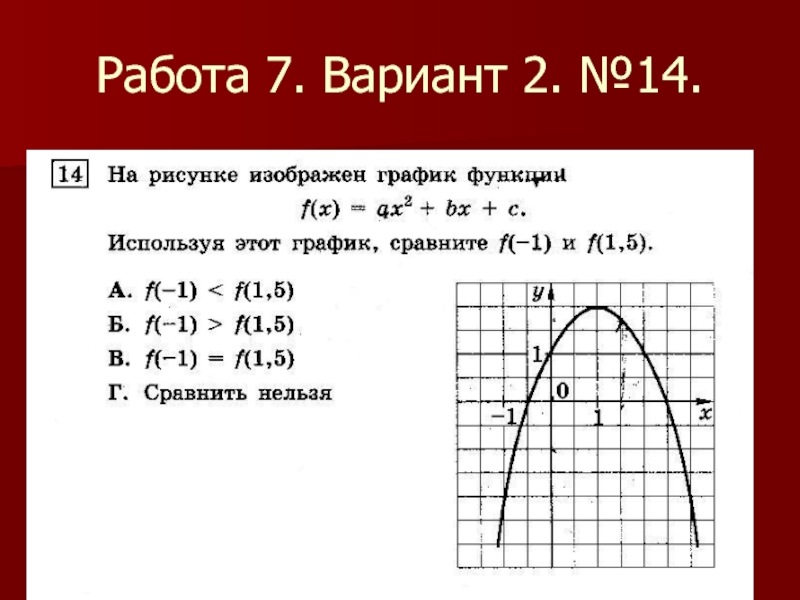
- 30. Работа 7. Вариант 2. №14.
- 31. Работа 7. Вариант 1. №15.
- 32. Работа 7. Вариант 2. №15.
- 33. Работа 8. Вариант 1. №15.
- 34. Работа 8. Вариант 2. №15.
- 35. Работа 9. Вариант 1. №15.
- 36. Работа 9. Вариант 2. №15.
- 37. Работа 10. Вариант 1. №15.
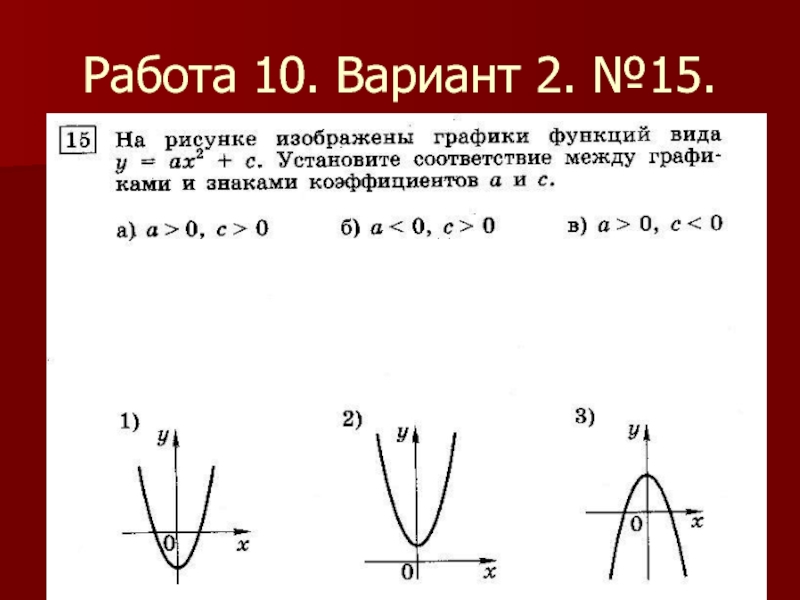
- 38. Работа 10. Вариант 2. №15.
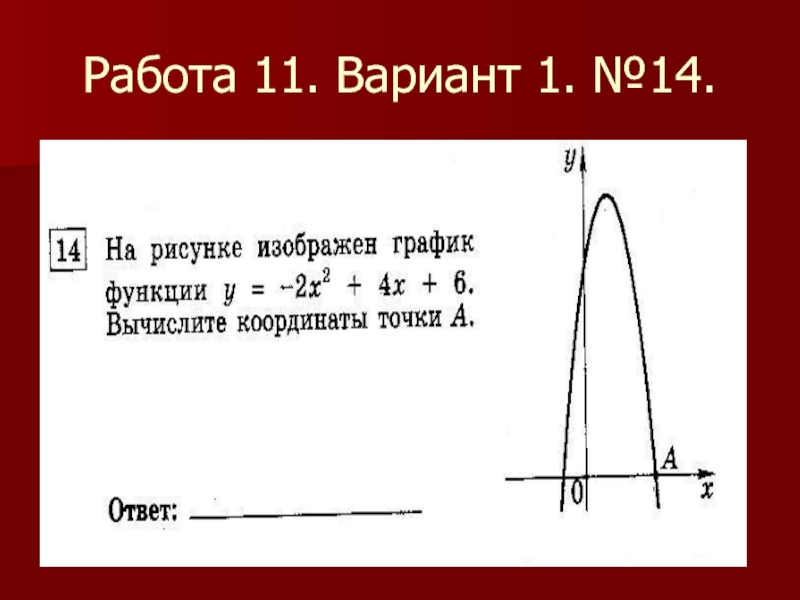
- 39. Работа 11. Вариант 1. №14.
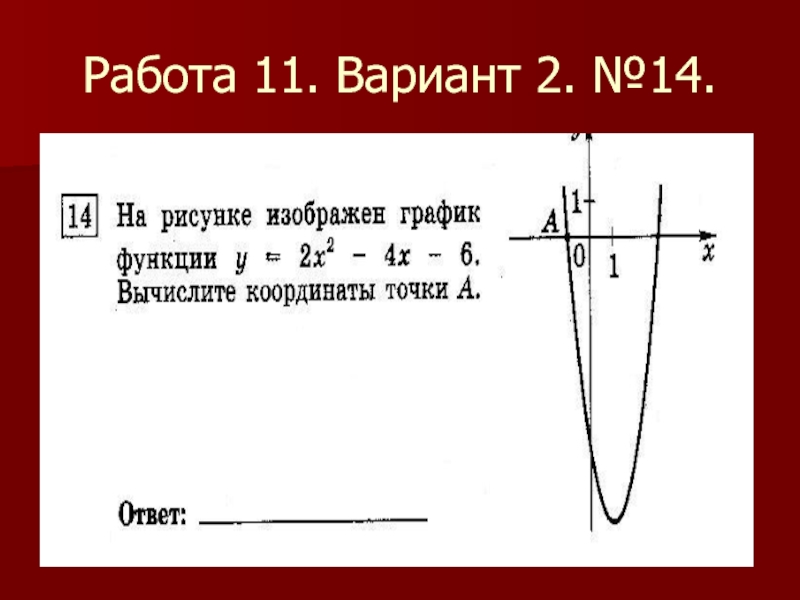
- 40. Работа 11. Вариант 2. №14.
- 41. Работа 11. Вариант 1. №15.
- 42. Работа 11. Вариант 2. №15.
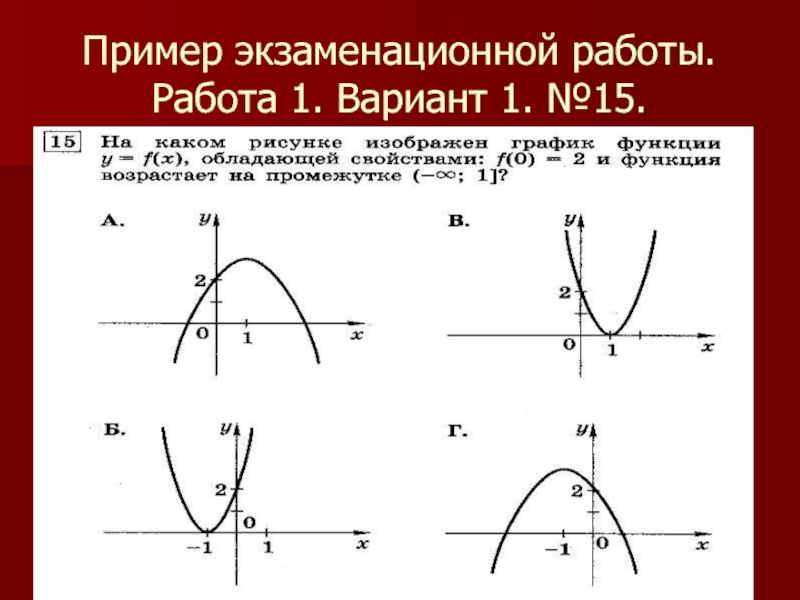
- 43. Пример экзаменационной работы. Работа 1. Вариант 1. №15.
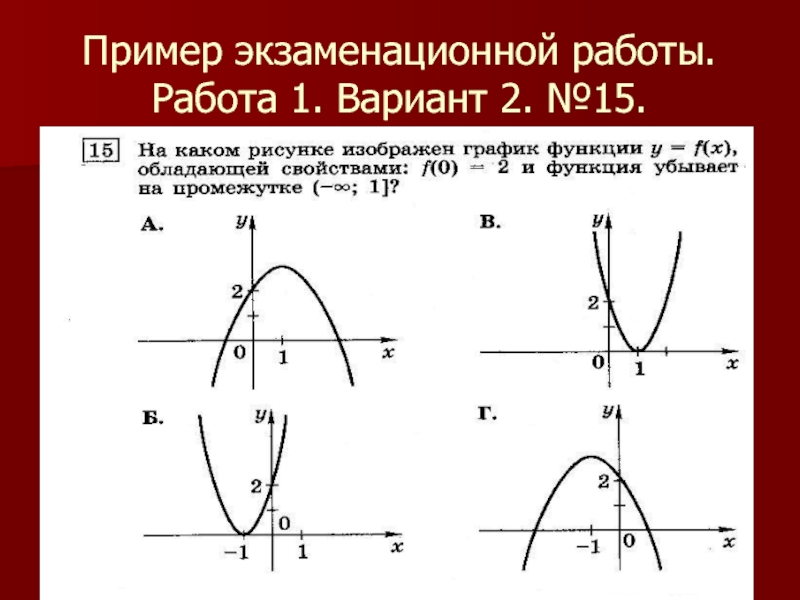
- 44. Пример экзаменационной работы. Работа 1. Вариант 2. №15.
- 45. Пример экзаменационной работы. Работа 2. Вариант 1. №15.
- 46. Пример экзаменационной работы. Работа 2. Вариант 2. №15.
Слайд 2Линейная функция
Линейной функцией называется функция, которую можно задать формулой у =
kх + b где х – независимая переменная, k и b – некоторые числа.
Ее областью определения называют множество всех действительных чисел.
График – прямая.
Число k – угловой коэффициент прямой.
Ее областью определения называют множество всех действительных чисел.
График – прямая.
Число k – угловой коэффициент прямой.
Слайд 3Расположение графика в зависимости от чисел k и b
K не
равно 0, то график функции у = kх + b пересекает ось х.
при K = 0 и b не равном нулю график функции параллелен оси х.
при K = 0 и b не равном нулю график функции параллелен оси х.
Слайд 4Расположение графика в зависимости от чисел k и b
k>0, то функция
возрастает.
k<0, то функция убывает
k<0, то функция убывает
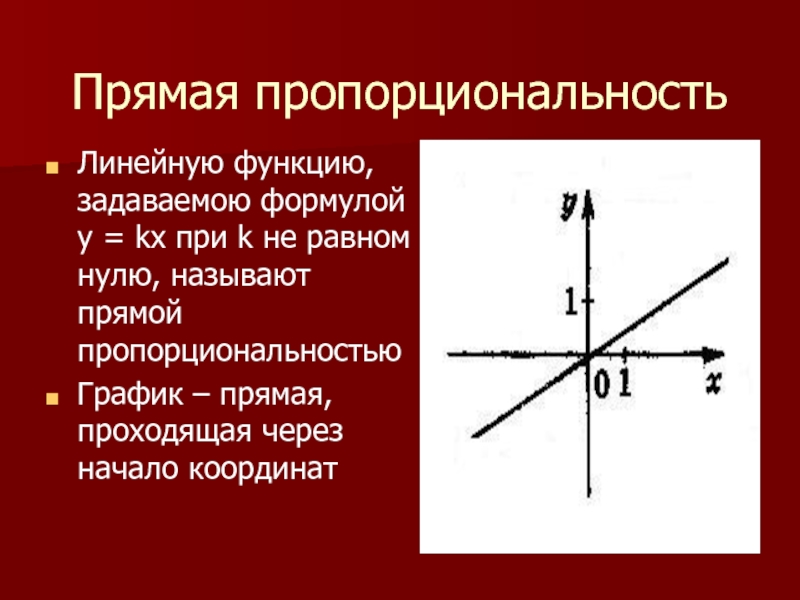
Слайд 5Прямая пропорциональность
Линейную функцию, задаваемою формулой у = kх при k не
равном нулю, называют прямой пропорциональностью
График – прямая, проходящая через начало координат
График – прямая, проходящая через начало координат
Слайд 6Обратная пропорциональность
Функция, которую можно задать формулой у = k/X, где х
– независимая переменная, k – не равное нулю число.
Область определения – множество всех действительных чисел, отличных от нуля.
График – гипербола.
Область определения – множество всех действительных чисел, отличных от нуля.
График – гипербола.
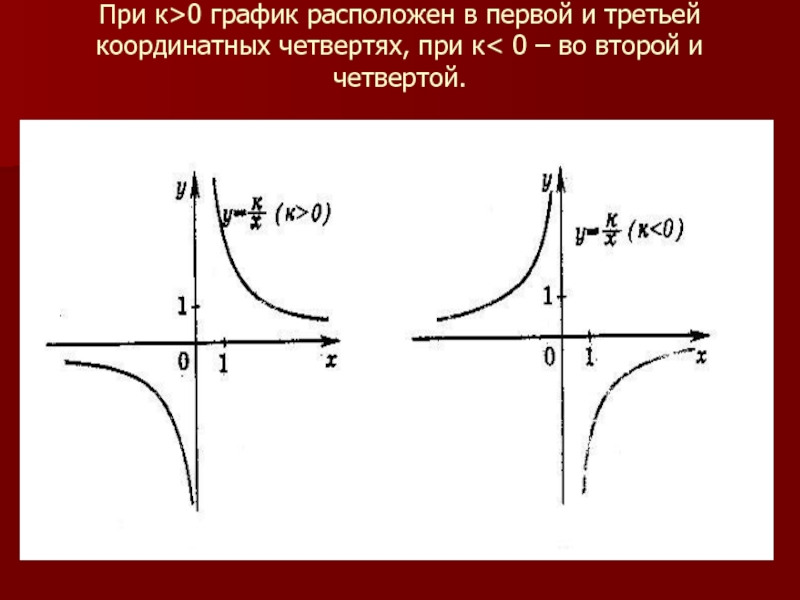
Слайд 7При к>0 график расположен в первой и третьей координатных четвертях, при
к< 0 – во второй и четвертой.
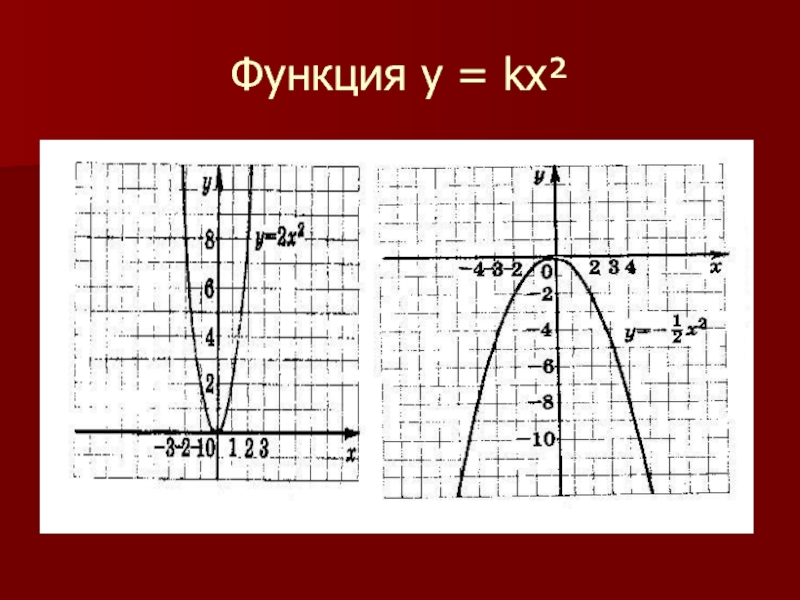
Слайд 8Функция у = х² и у = kх²
Область определения –
множество всех действительных чисел.
Функция обращается в нуль при х=0.
График функции - парабола.
При k>0 график проходит через начало координат и расположен в первой и во второй координатных четвертях. Ветви параболы направлены вверх.
При k<0 график проходит через начало координат и расположен в третьей и в четвертой координатных четвертях. Ветви параболы направлены вниз.
Функция обращается в нуль при х=0.
График функции - парабола.
При k>0 график проходит через начало координат и расположен в первой и во второй координатных четвертях. Ветви параболы направлены вверх.
При k<0 график проходит через начало координат и расположен в третьей и в четвертой координатных четвертях. Ветви параболы направлены вниз.
Слайд 10Функция у = х³
Область определения – множество всех действительных чисел.
Функция обращается
в нуль при х=0, принимает отрицательные значения, если х<0, и положительные значения, если х >0.
График функции проходит через начало координат и расположен в первой и третьей координатных четвертях.
График симметричен относительно начала координат.
График функции проходит через начало координат и расположен в первой и третьей координатных четвертях.
График симметричен относительно начала координат.
Слайд 11Функция у = |х|
Область определения – множество всех чисел.
|х| = х,
если х >=0.
|х| = -х, если х <=0.
|х| = -х, если х <=0.
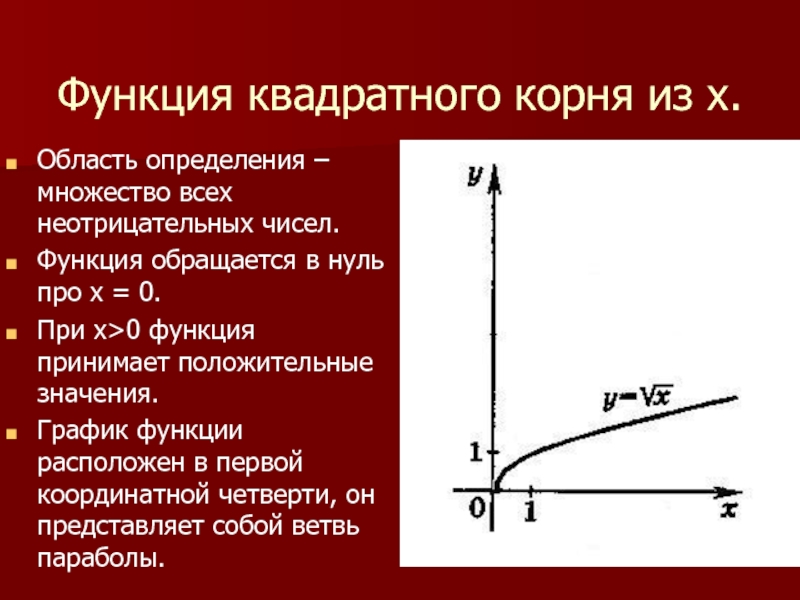
Слайд 12Функция квадратного корня из х.
Область определения – множество всех неотрицательных чисел.
Функция
обращается в нуль про х = 0.
При х>0 функция принимает положительные значения.
График функции расположен в первой координатной четверти, он представляет собой ветвь параболы.
При х>0 функция принимает положительные значения.
График функции расположен в первой координатной четверти, он представляет собой ветвь параболы.