- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Формулы приведения. презентация
Содержание
- 1. Формулы приведения.
- 2. x
- 3. Значения тригонометрических функций любых углов поворота можно
- 4. В градусной мере: В радианах: 10200=900·11+300=900·12–600 1020
- 5. Осталось разобраться со знаком ± перед каждым
- 6. В первом случае нам придется
- 7. Значит, Пример 2. Все этапы решения проделайте
- 8. Пример 3. Привести к значению тригонометрической функции
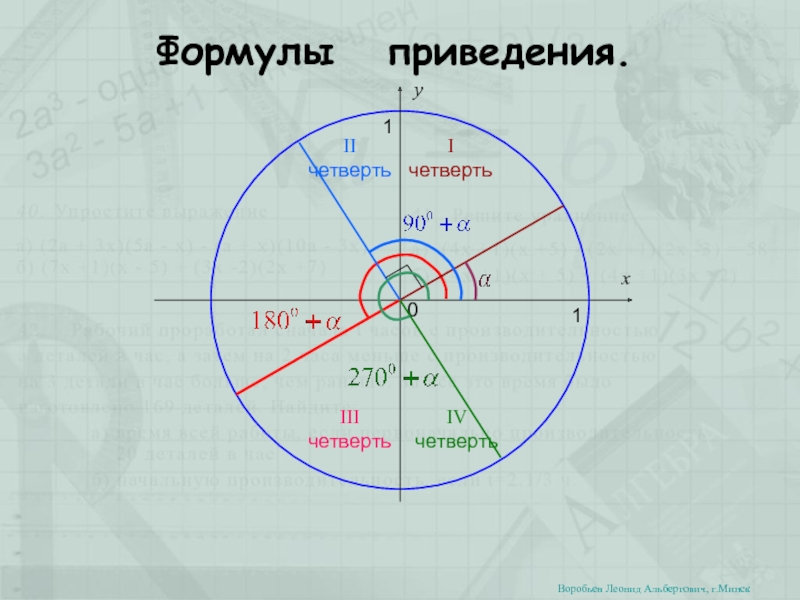
Слайд 1Формулы приведения.
0
1
1
x
y
I четверть
II четверть
III четверть
IV четверть
Воробьев Леонид Альбертович, г.Минск
Слайд 2
x
y
0
cosα
sinα
α
900+α
1800+α
2700+α
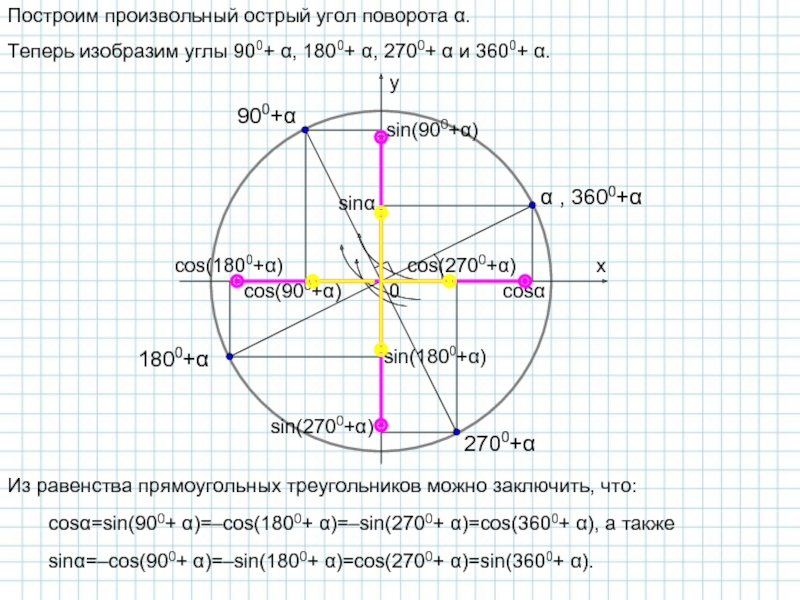
Построим произвольный острый угол поворота α.
Теперь изобразим углы 900+ α,
сos(900+α)
sin(900+α)
сos(1800+α)
sin(1800+α)
sin(2700+α)
cos(2700+α)
, 3600+α
Из равенства прямоугольных треугольников можно заключить, что:
cosα=sin(900+ α)=–cos(1800+ α)=–sin(2700+ α)=cos(3600+ α), а также
sinα=–cos(900+ α)=–sin(1800+ α)=cos(2700+ α)=sin(3600+ α).
Слайд 3Значения тригонометрических функций любых углов поворота можно привести к значению тригонометрических
С первым столбцом все ясно – в нем известные Вам тригонометрические функции. Во втором столбце показано, что любой аргумент(угол) этих функций можно представить в таком виде. Поясним это на конкретных примерах:
Слайд 4В градусной мере:
В радианах:
10200=900·11+300=900·12–600
1020
90
11
90
120
90
30
Как видите мы использовали известное Вам с начальной
Умножьте полученные сумму или разность на и получите искомые выражения.
В любом случае мы добились следующего: наш аргумент тригонометрической функции представлен в виде целого числа прямых углов плюс или минус какой-то острый угол.
Обратим теперь внимание на 3-й и 4-й столбцы таблицы. Сразу заметим, что в случае четного числа прямых углов тригонометрическая функция остается такой же, а в случае нечетного числа – изменяется на кофункцию (sin на cos, tg на ctg и наоборот), причем аргументом этой функции является остаток.
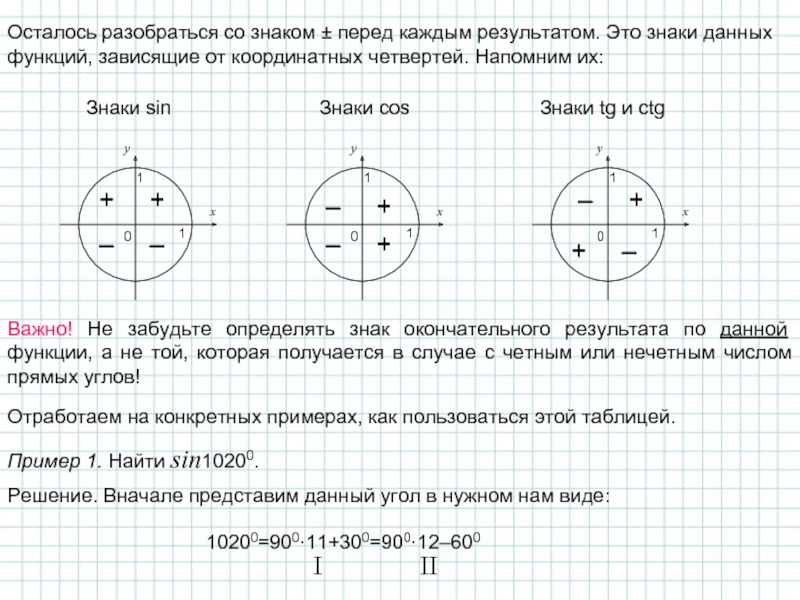
Слайд 5Осталось разобраться со знаком ± перед каждым результатом. Это знаки данных
х
0
у
1
1
х
0
у
1
1
х
0
у
1
1
Знаки sin
Знаки cos
Знаки tg и ctg
+
+
+
+
+
+
–
–
–
–
–
–
Важно! Не забудьте определять знак окончательного результата по данной функции, а не той, которая получается в случае с четным или нечетным числом прямых углов!
Отработаем на конкретных примерах, как пользоваться этой таблицей.
Пример 1. Найти sin10200.
Решение. Вначале представим данный угол в нужном нам виде:
10200=900·11+300=900·12–600
I
II
Слайд 6
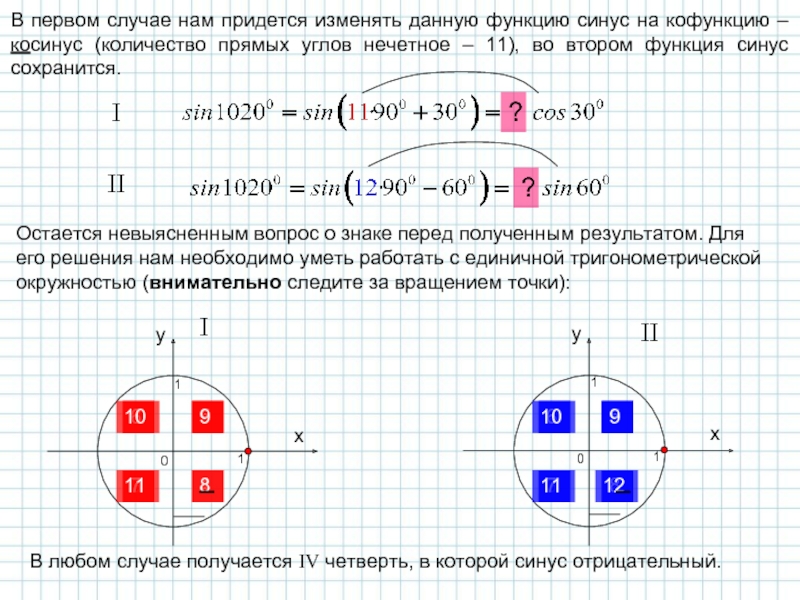
В первом случае нам придется изменять данную функцию синус на кофункцию
I
II
Остается невыясненным вопрос о знаке перед полученным результатом. Для его решения нам необходимо уметь работать с единичной тригонометрической окружностью (внимательно следите за вращением точки):
?
?
х
у
0
1
1
х
у
0
1
1
I
II
1
2
3
4
5
6
7
8
9
10
11
1
2
3
4
5
6
7
8
9
10
11
12
В любом случае получается IV четверть, в которой синус отрицательный.
–
–
Слайд 7Значит,
Пример 2. Все этапы решения проделайте самостоятельно (под контролем учителя).
Решение:
В случаях,
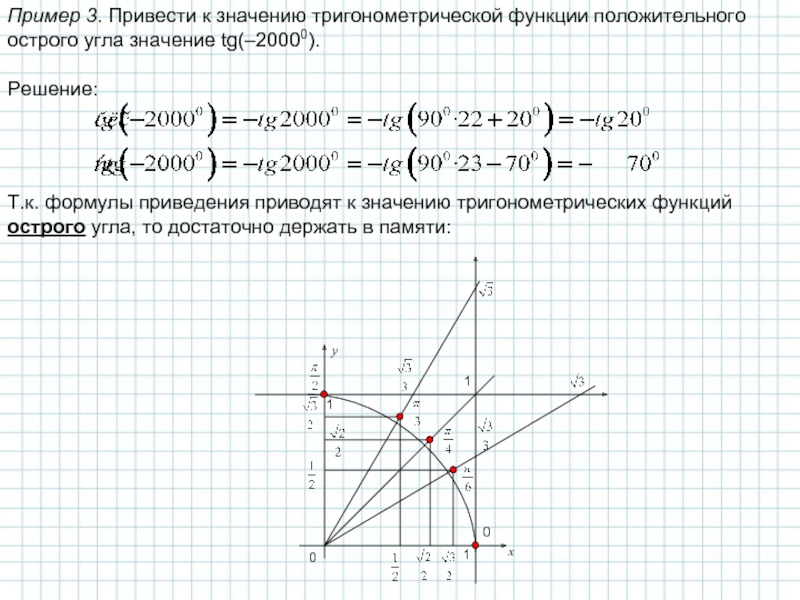
Слайд 8Пример 3. Привести к значению тригонометрической функции положительного острого угла значение
Решение:
Т.к. формулы приведения приводят к значению тригонометрических функций острого угла, то достаточно держать в памяти: