- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Формулы для вычисления площадей различных треугольников презентация
Содержание
- 1. Формулы для вычисления площадей различных треугольников
- 2. Ответить на вопросы: 1. Перечислите
- 3. Найдите ошибки в тексте: Треугольник
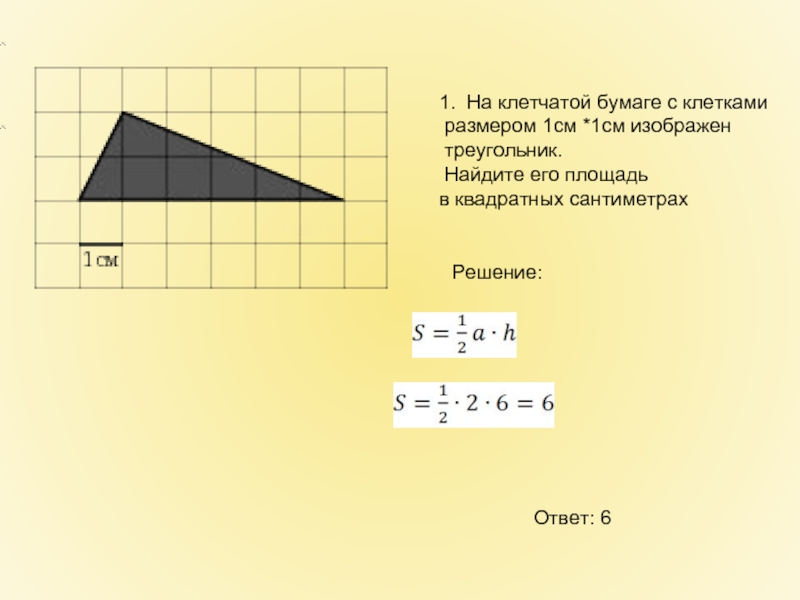
- 4. 1. На клетчатой бумаге с клетками
- 5. Площадь любого треугольника. А a B C
- 6. 2. Найдите площадь прямоугольного треугольника,
- 7. Площадь прямоугольного треугольника. ПЛОЩАДЬ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА РАВНА ПОЛОВИНЕ ПРОИЗВЕДЕНИЯ КАТЕТОВ. b a
- 8. Если в треугольнике известны две стороны
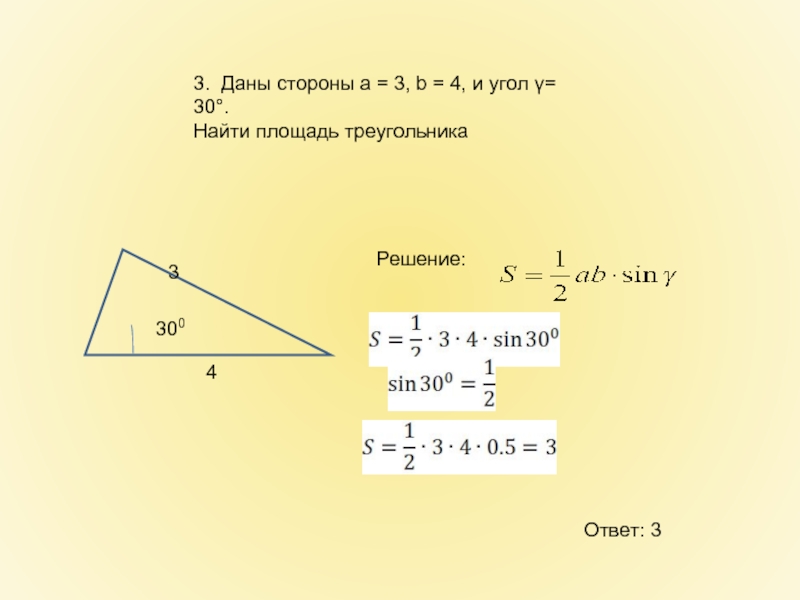
- 9. 3. Даны стороны a = 3, b
- 10. 4. Дан равносторонний треугольник со стороной a=
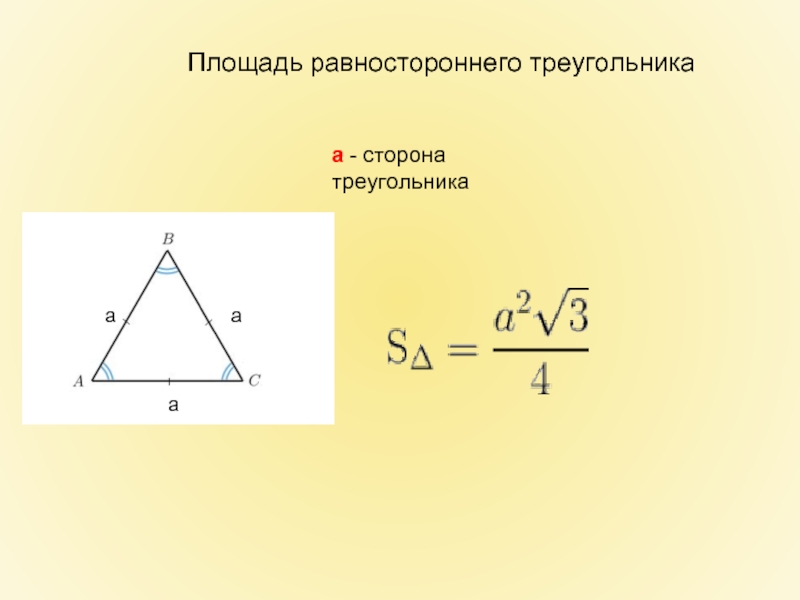
- 11. Площадь равностороннего треугольника a - сторона треугольника а а а
- 12. Пример расчета площади равностороннего треугольника через сторону.
- 13. Одна из книг Герона была названа
- 14. I формула Герона b с a Где
- 15. Дан треугольник со сторонами 13, 14, 15.
- 16. c b a II формула Герона
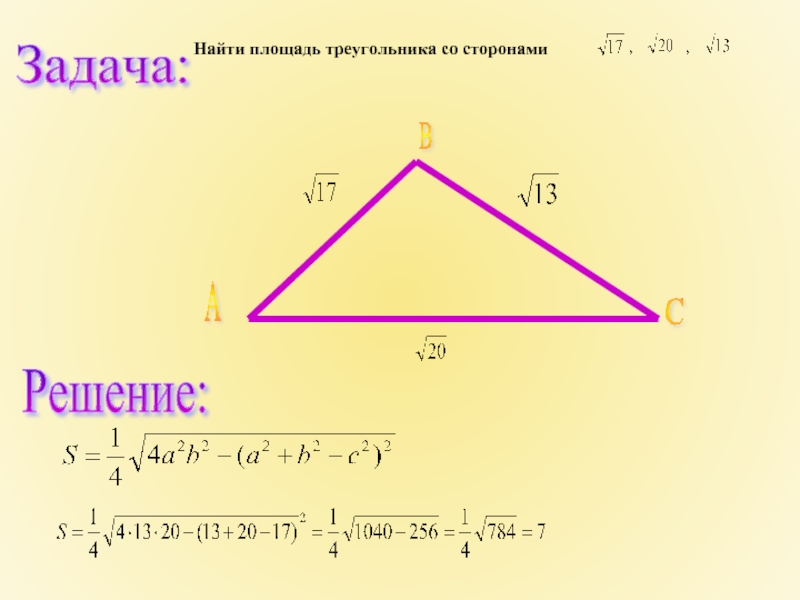
- 17. Найти площадь треугольника со сторонами Решение:
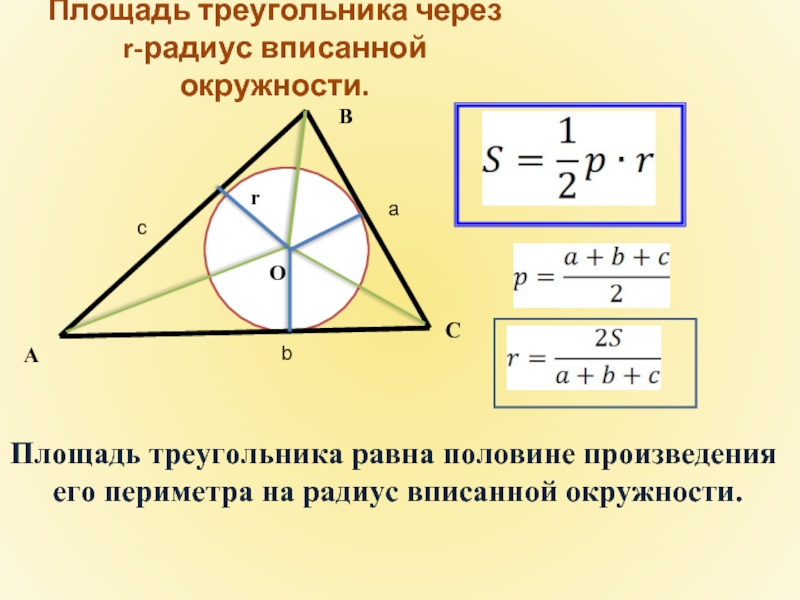
- 18. Площадь треугольника через r-радиус вписанной окружности.
- 19. Площадь треугольника через R-радиус описанной
- 20. В треугольнике ABC АС = 4, ВС =
- 21. Задача : Вычислите площадь данного треугольника.
- 22. Площадь искомого треугольника найдем по формуле
- 23. В
- 24. Георг Алекса́ндр Пик ( 10 августа 1859
- 28. Формула Пика имеет ряд преимуществ перед
- 29. Площадь треугольника в системе координат Найти площадь
- 31. Задача: А(0;0), В(5:7), С(4:-2). Найти площадь треугольника. Отв.19. Решение:
- 32. Десять формул для нахождения площадей различных треугольников.
- 33. Интернет-ресурсы Сайт http://www.webmath.ru Вычисление площади треугольника
Слайд 2Ответить на вопросы:
1. Перечислите элементы треугольника.
2. Назовите виды треугольников по углам.
3.
4. Какой треугольник называется равно бедренным?
5. Какой треугольник называется равносторонним?
Слайд 3Найдите ошибки в тексте:
Треугольник – это геометрическая фигура, состоящая из трех
Среди треугольников особенно выделяется равнобедренный треугольник. Если в нем провести любую биссектрису, она будет являться медианой и высотой.
Слайд 4
1. На клетчатой бумаге с клетками
размером 1см *1см изображен
треугольник.
в квадратных сантиметрах
Решение:
Ответ: 6
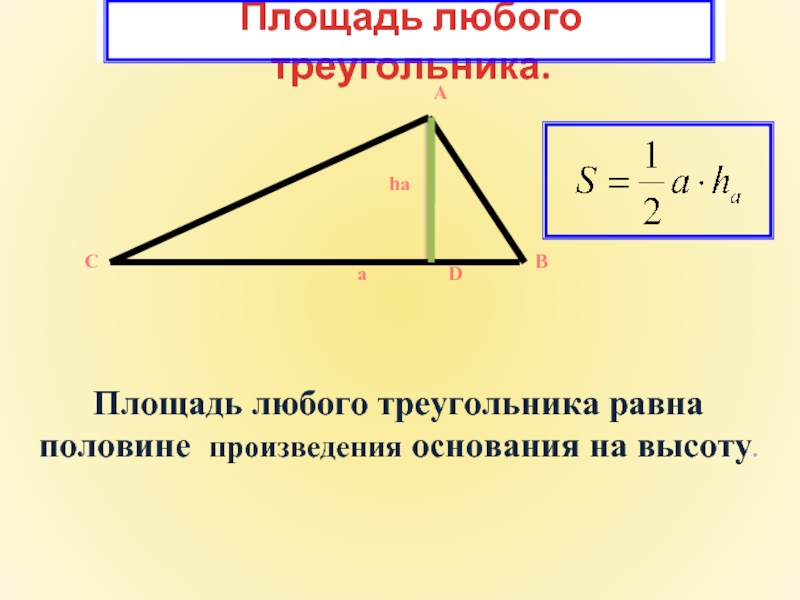
Слайд 5Площадь любого треугольника.
А
a
B
C
D
ha
Площадь любого треугольника равна
половине произведения основания на высоту.
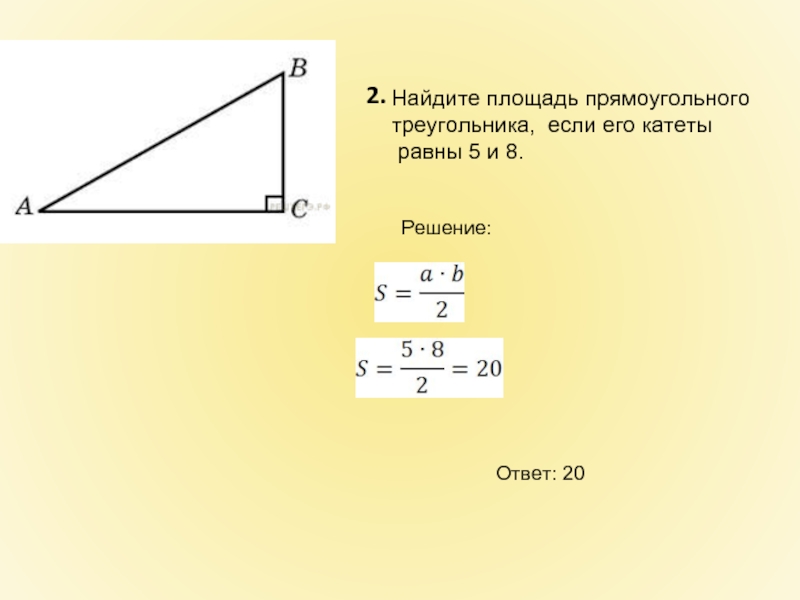
Слайд 6 2.
Найдите площадь прямоугольного
треугольника, если его катеты
равны 5 и
Решение:
Ответ: 20
Слайд 7Площадь прямоугольного треугольника.
ПЛОЩАДЬ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА РАВНА ПОЛОВИНЕ
ПРОИЗВЕДЕНИЯ КАТЕТОВ.
b
a
Слайд 8Если в треугольнике известны две стороны
и угол между ними, то
ɣ
a
b
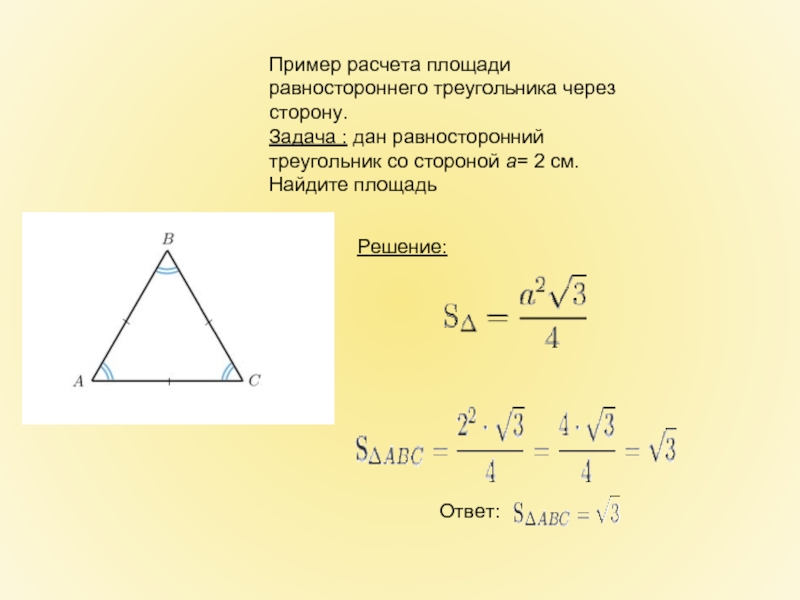
Слайд 12Пример расчета площади равностороннего треугольника через сторону. Задача : дан равносторонний треугольник со
Решение:
Ответ:
Слайд 13
Одна из книг Герона была названа им «Геометрика» и является своего
Имя Герона навсегда связано с известной формулой нахождения площади треугольника, если даны три его стороны a,b,c:
Одним из поздних греческих математиков – энциклопедистов, труды которого имели главным образом прикладной характер, был Герон Александрийский, живший в 1 в. н. э.
Слайд 15Дан треугольник со сторонами 13, 14, 15.
Найдите высоту, проведённую к
Пусть AH — указанная высота треугольника ABC
со сторонами BC = 15, AC = 14, AB = 13.
А
В
С
Н
По формуле Герона
S =
=
= 7 . 3 . 4 = 84.
=
С другой стороны,
Откуда находим, что
Ответ: 11,2
Решение:
Слайд 18Площадь треугольника через
r-радиус вписанной окружности.
Площадь треугольника равна половине произведения
его
А
B
C
O
r
a
b
с
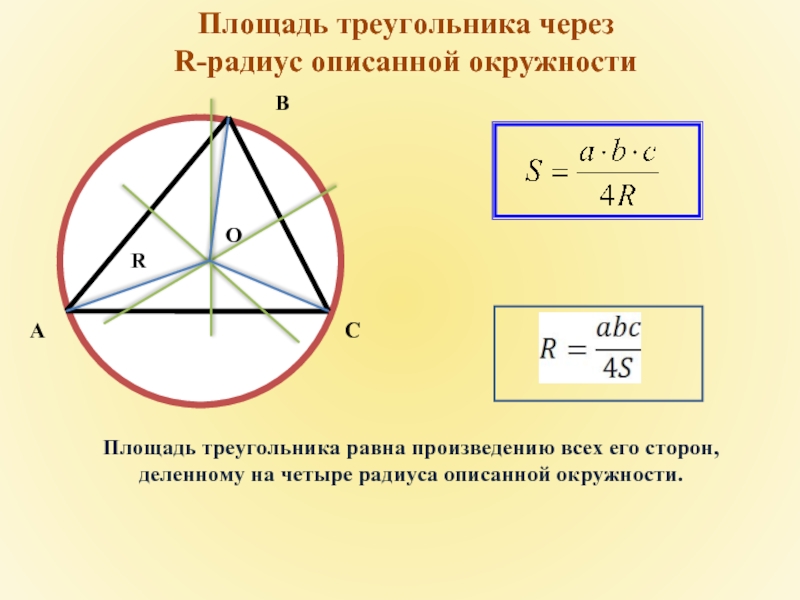
Слайд 19
Площадь треугольника через
R-радиус описанной окружности
Площадь треугольника равна произведению всех его
деленному на четыре радиуса описанной окружности.
A
B
C
O
R
Слайд 20В треугольнике ABC АС = 4, ВС = 3, угол C равен 900.
Найдите
Решение:
Воспользуемся формулой
радиуса окружности
вписанной в треугольник:
По теореме Пифагора:
Найдём площадь:
Таким образом:
Ответ: 1 и 2,5
4
3
Слайд 21
Задача : Вычислите площадь данного треугольника.
Решение:
Sпрямоугольника = 6*5 = 30 ,
S2 = ½ *4*2=4
S3=½*6*3 = 9 Тогда
Sтр = Sпр - S1 - S2 - S3 =
=30 – 5 – 4 – 9 = 12
Ответ:12
Если треугольник будет иметь другое расположение, то основание и высоту в таком треугольнике определить точно невозможно, а, следовательно, невозможно применить формулу для вычисления его площади. Поэтому здесь можно только применить способ вычитания прямоугольных треугольников из площади прямоугольника. .
S1
S3
S2
Слайд 22
Площадь искомого треугольника найдем по формуле Пика:
где Г –количество узлов на границе треугольника(на сторонах и вершинах),
В – количество узлов внутри треугольника.
Г = 12, В = 10
Получаем S=12/2+10-1=15
Ответ: 15
Формула Пика
о
о
о
о
о
о
о
о
о
о
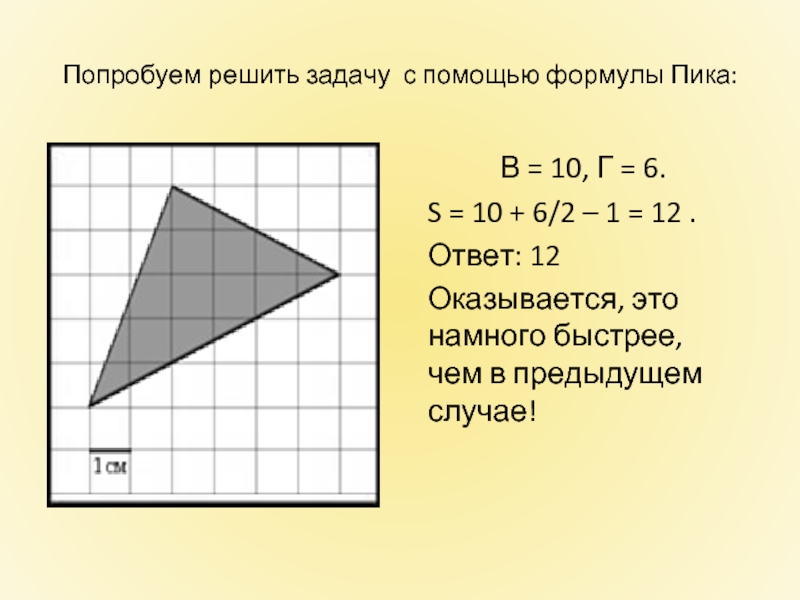
Слайд 23
В = 10, Г = 6.
S
Ответ: 12
Оказывается, это намного быстрее, чем в предыдущем случае!
Попробуем решить задачу с помощью формулы Пика:
Слайд 24Георг Алекса́ндр Пик ( 10 августа 1859 — 13 июля 1942)
Круг математических интересов Пика был чрезвычайно широк. Им написаны работы в области математического анализа, дифференциальной геометрии, в теории дифференциальных уравнений и т. д., всего более 50 тем.
Широкую известность получила открытая им в 1899 году теорема Пика для расчёта площади многоугольника. В Германии эта теорема включена в школьные учебники.
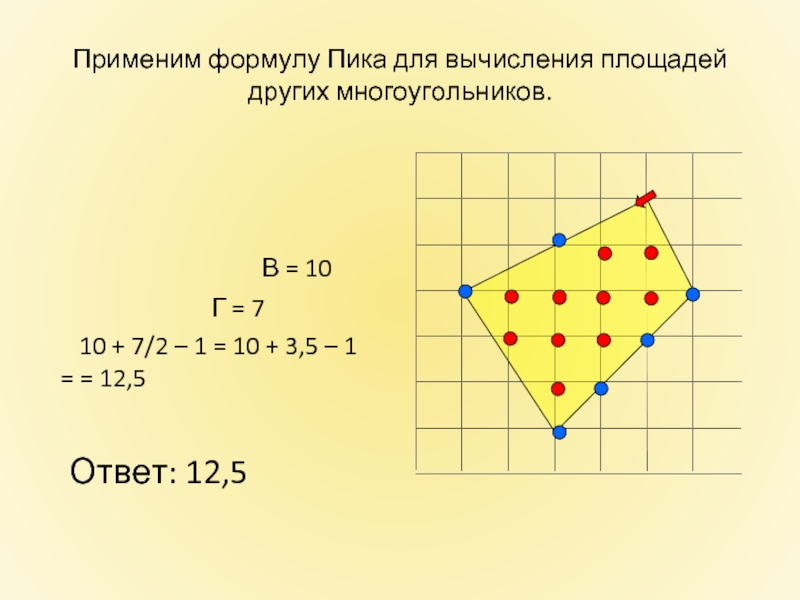
Слайд 25
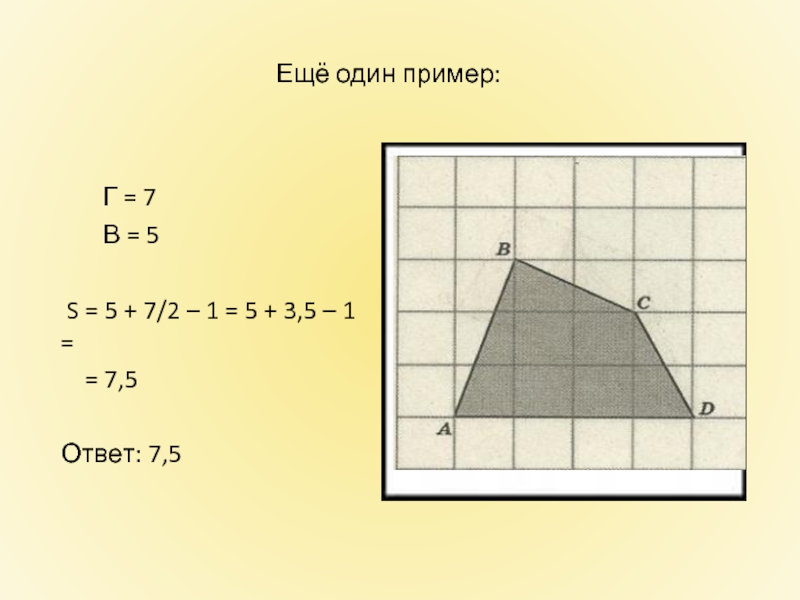
Г = 7
10 + 7/2 – 1 = 10 + 3,5 – 1 = = 12,5
Ответ: 12,5
Применим формулу Пика для вычисления площадей других многоугольников.
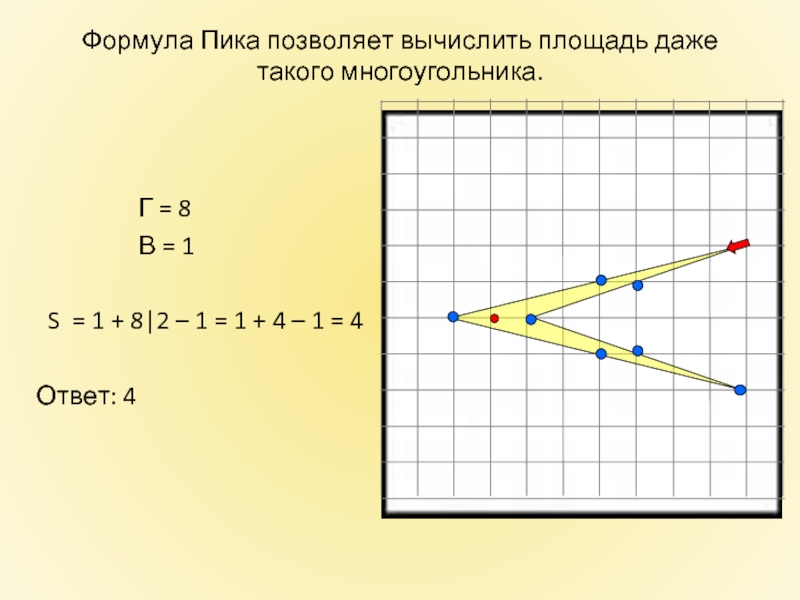
Слайд 26
Г
В = 1
S = 1 + 8|2 – 1 = 1 + 4 – 1 = 4
Ответ: 4
Формула Пика позволяет вычислить площадь даже такого многоугольника.
Слайд 28
Формула Пика имеет ряд преимуществ перед другими способами вычисления площадей многоугольников
1. Для вычисления площади многоугольника, нужно знать всего одну формулу: : S = В + Г/2 - 1 .
2. Формула Пика очень проста для запоминания.
3. Формула Пика очень удобна и проста в применении.
4. Многоугольник, площадь которого необходимо вычислить, может быть любой, даже самой причудливой формы.
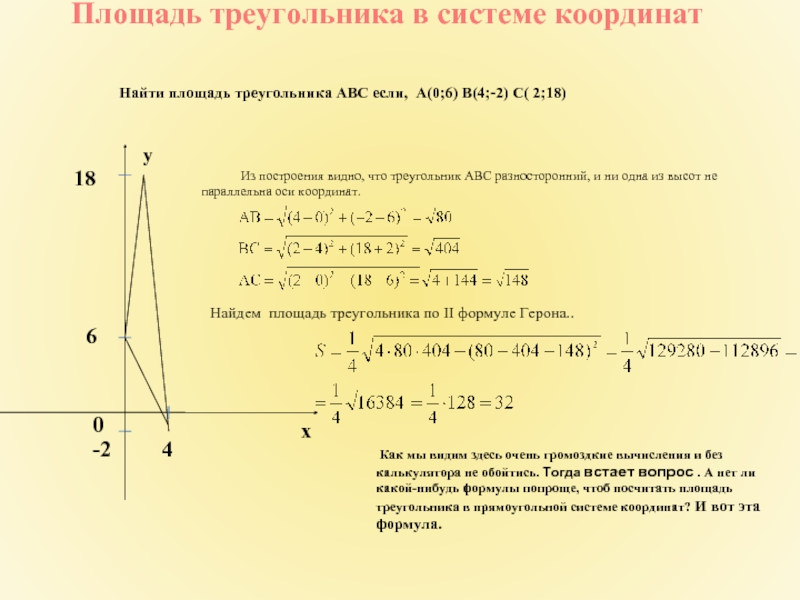
Слайд 29Площадь треугольника в системе координат
Найти площадь треугольника АВС если, А(0;6) B(4;-2)
Из построения видно, что треугольник АВС разносторонний, и ни одна из высот не параллельна оси координат.
Найдем площадь треугольника по II формуле Герона..
Как мы видим здесь очень громоздкие вычисления и без калькулятора не обойтись. Тогда встает вопрос . А нет ли какой-нибудь формулы попроще, чтоб посчитать площадь треугольника в прямоугольной системе координат? И вот эта формула.
Слайд 30
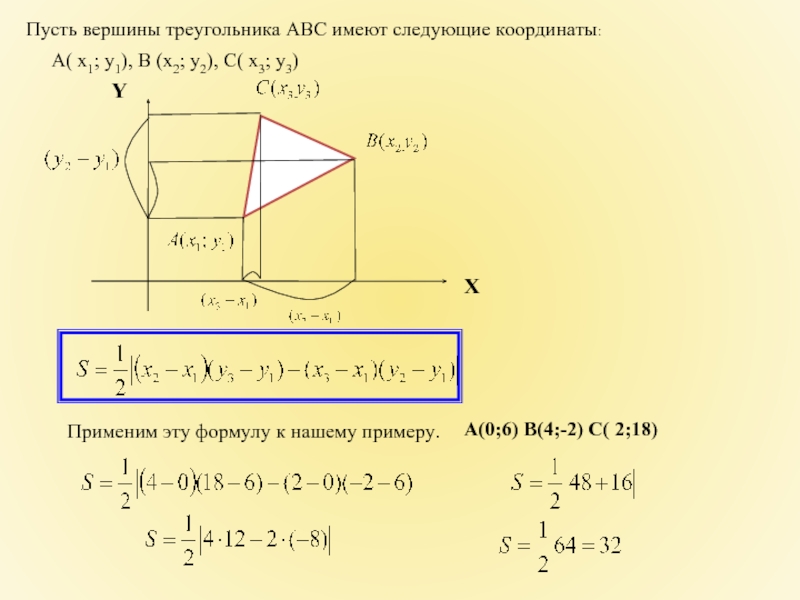
Применим эту формулу к нашему примеру.
Пусть вершины треугольника АВС имеют следующие координаты:
А( х1; у1), В (х2; у2), С( х3; у3)
А(0;6) B(4;-2) C( 2;18)