Эпюр3 презентация

Содержание

1. Эпюр3
2. Наиболее общий способ построения линии пересечения двух
4. Повторяя указанный прием с различными вспомогательными поверхностями,
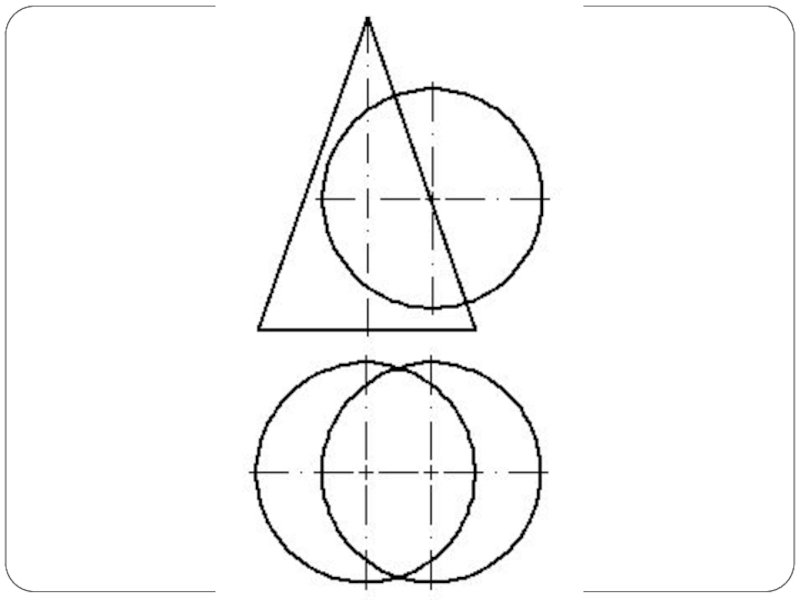
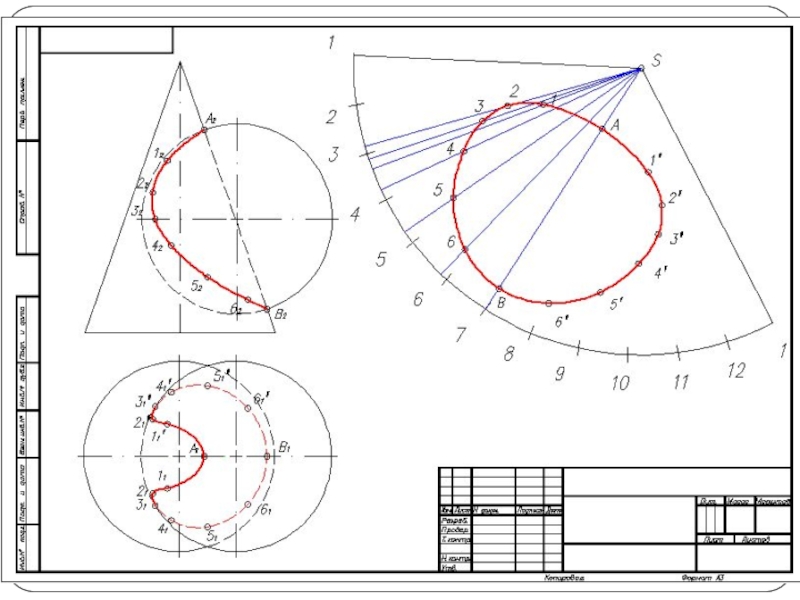
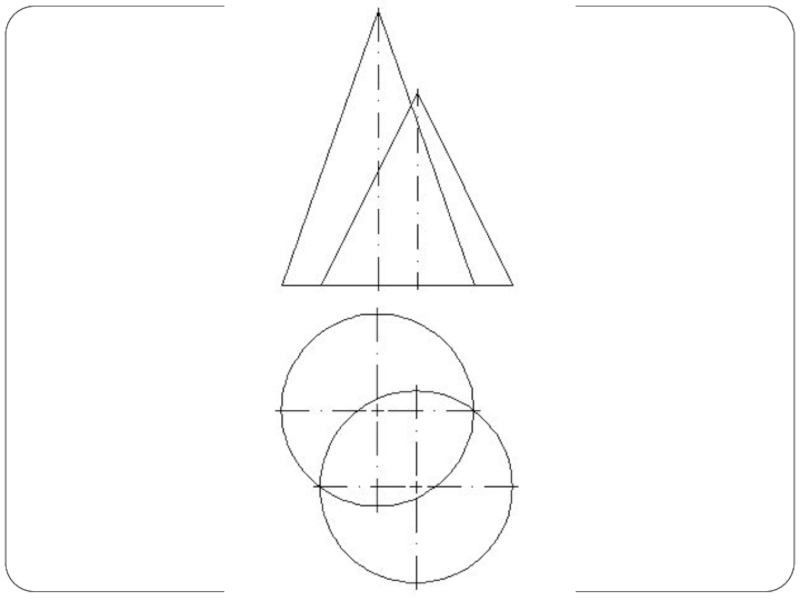
5. Построить линию пересечения поверхности прямого кругового конуса
8. Круговой конус и сфера
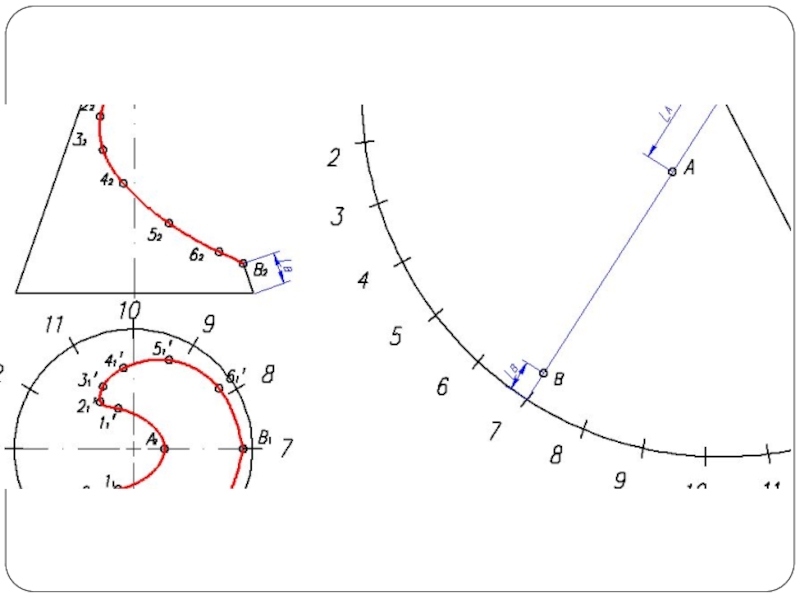
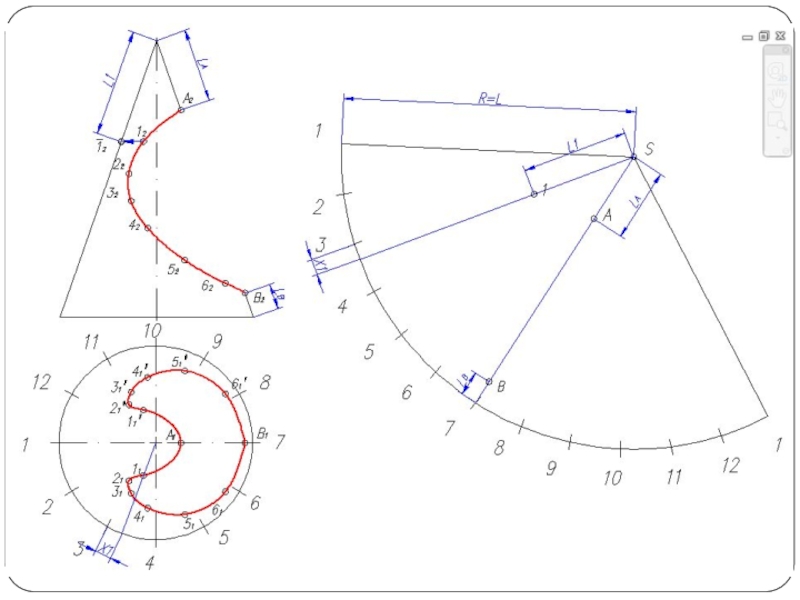
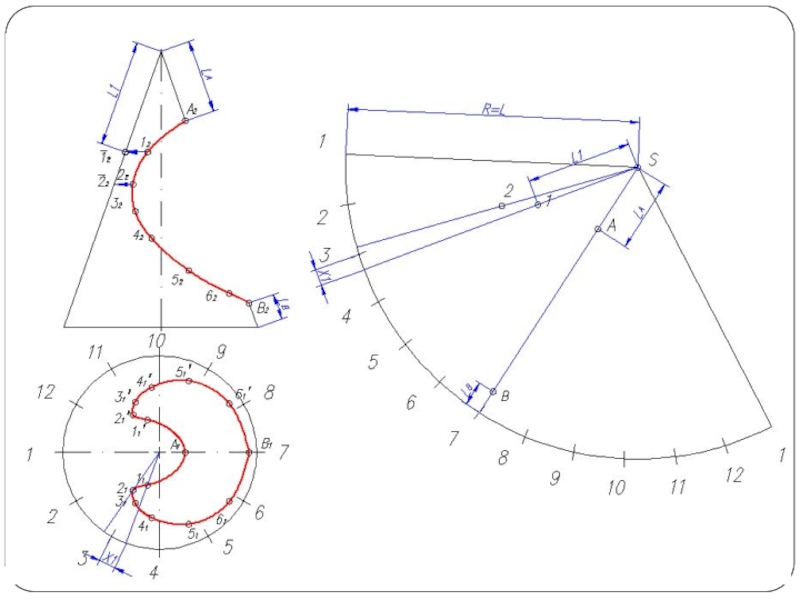
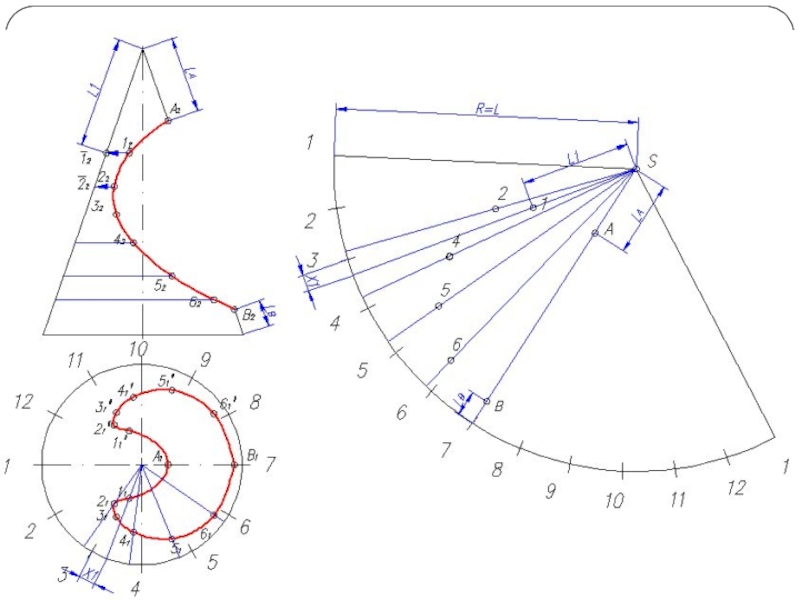
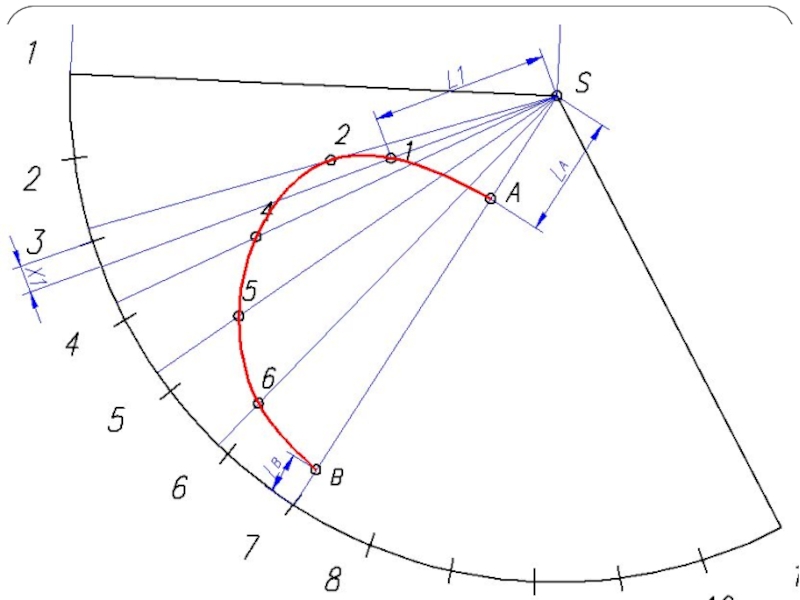
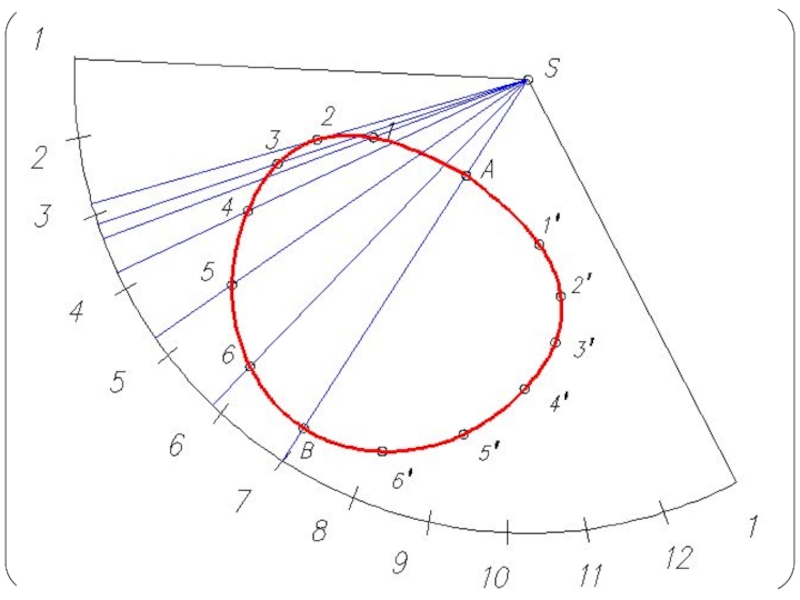
26. Построение развертки конуса Разверткой называется плоская фигура,
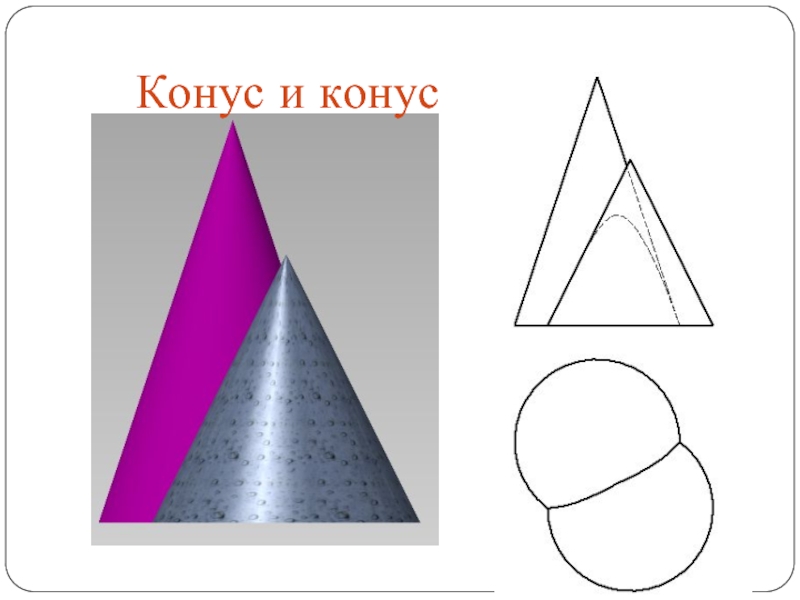
39. Конус и конус
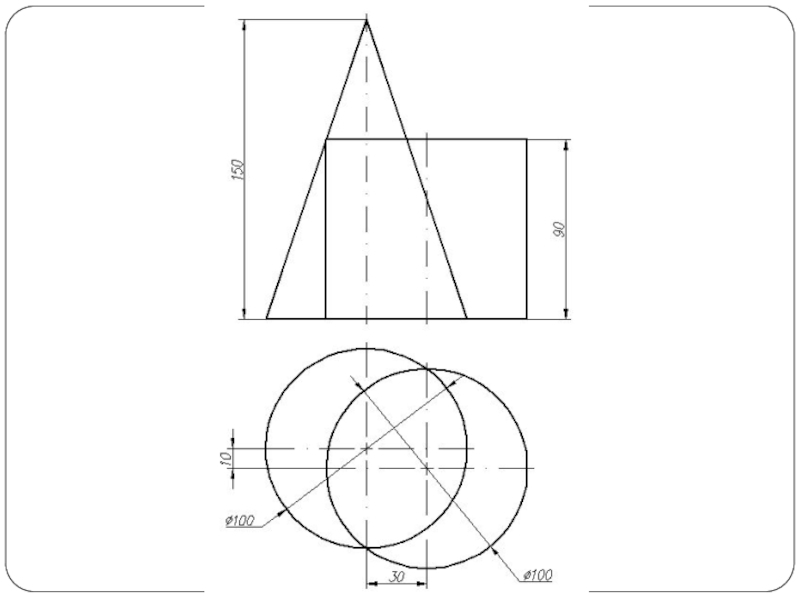
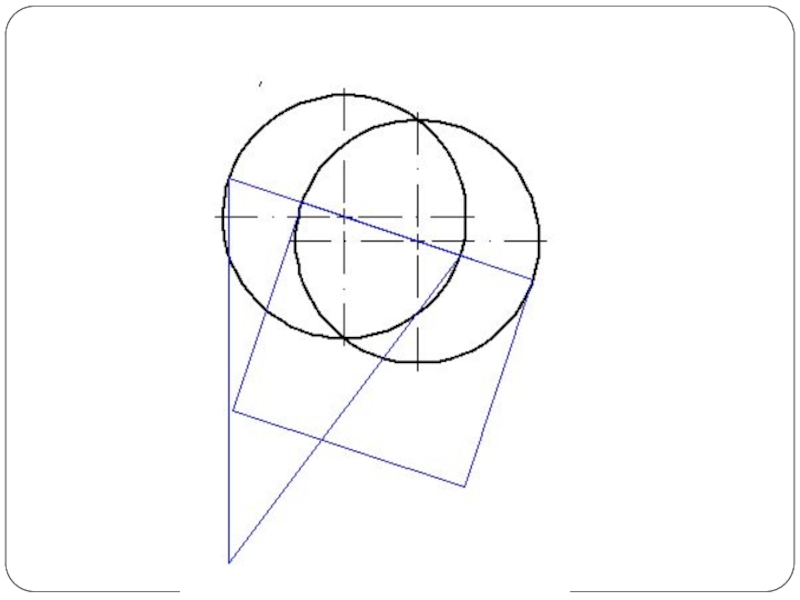
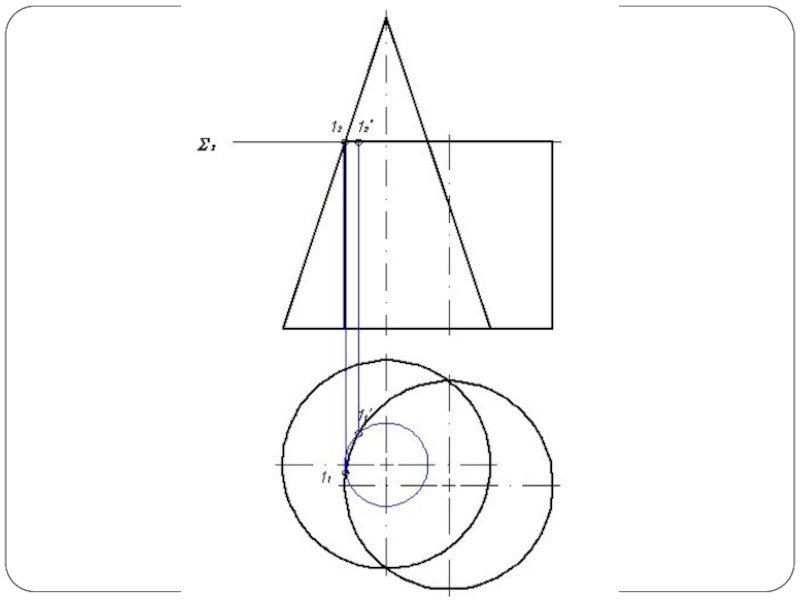
48. Круговой конус и горизонтально-проецирующий цилиндр
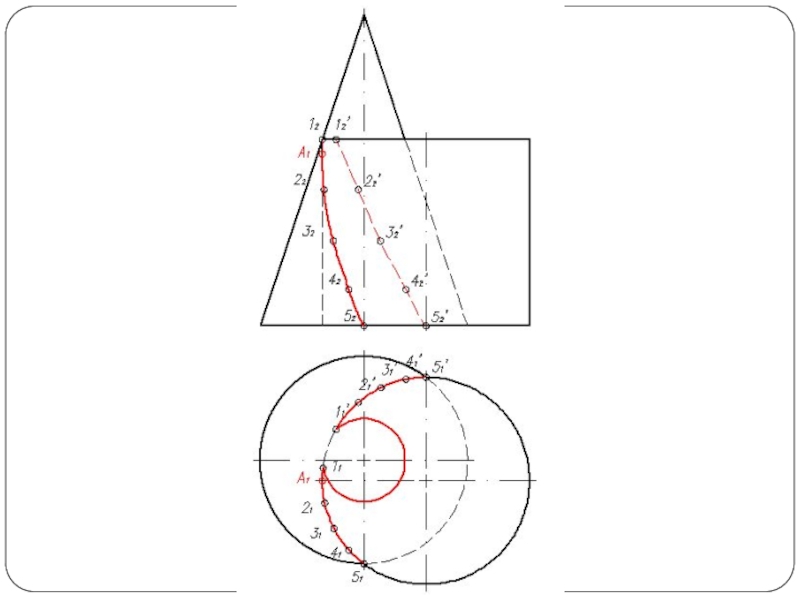
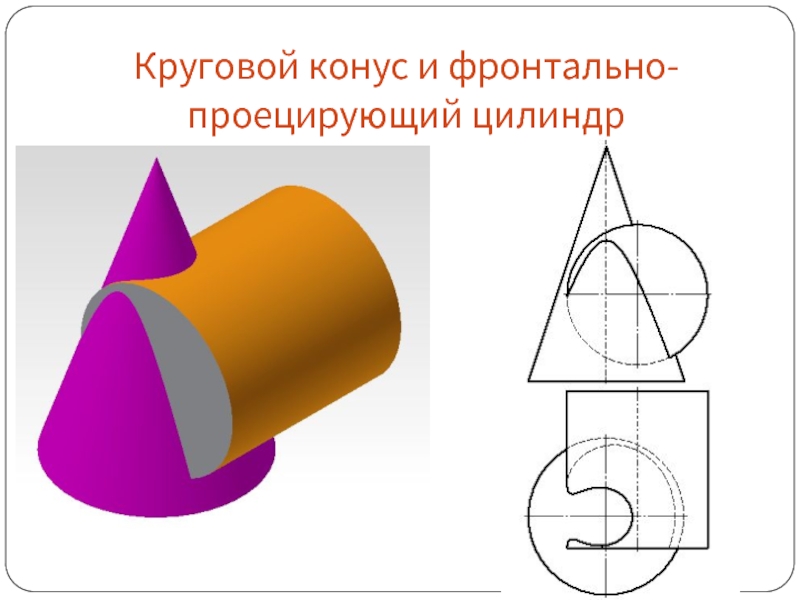
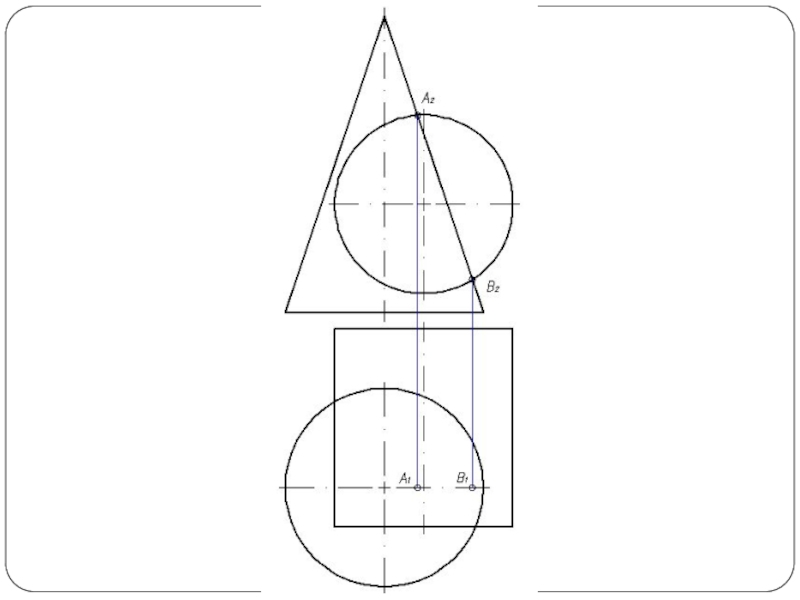
57. Круговой конус и фронтально-проецирующий цилиндр

Слайд 1Пересечение поверхностей

Построение развертки

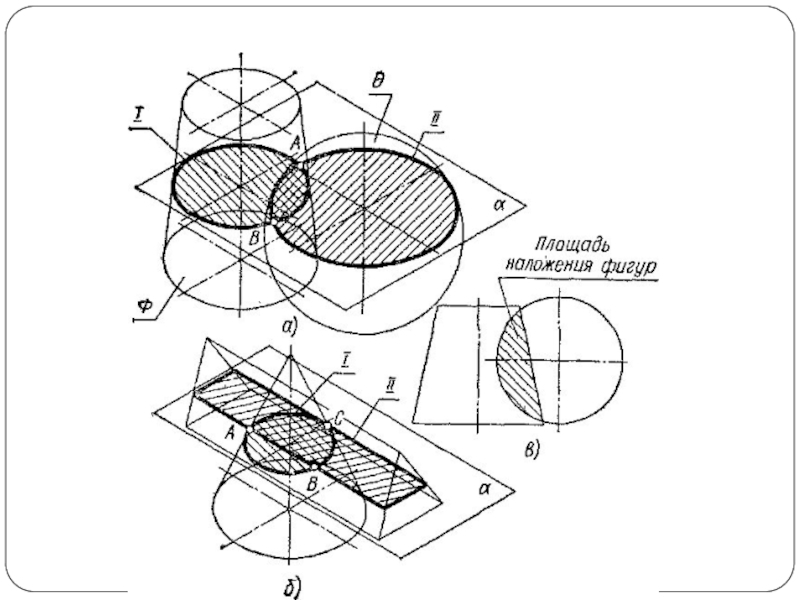
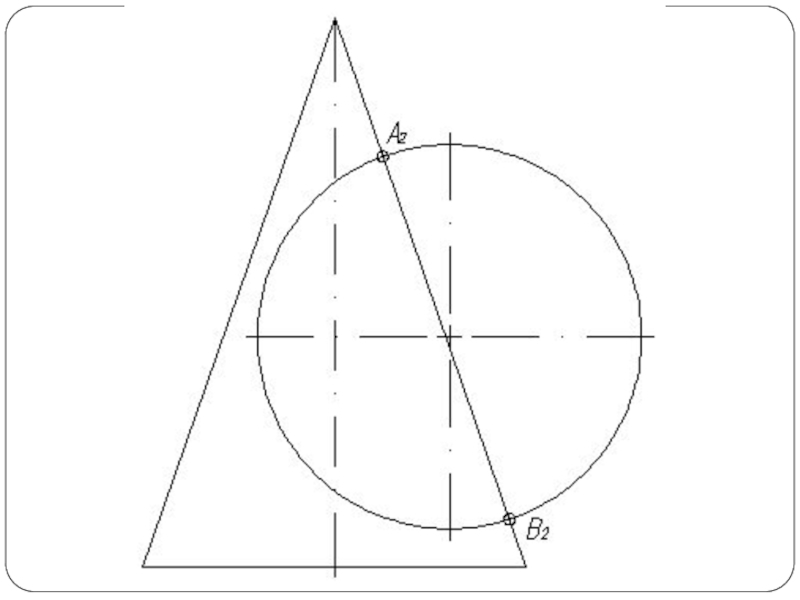
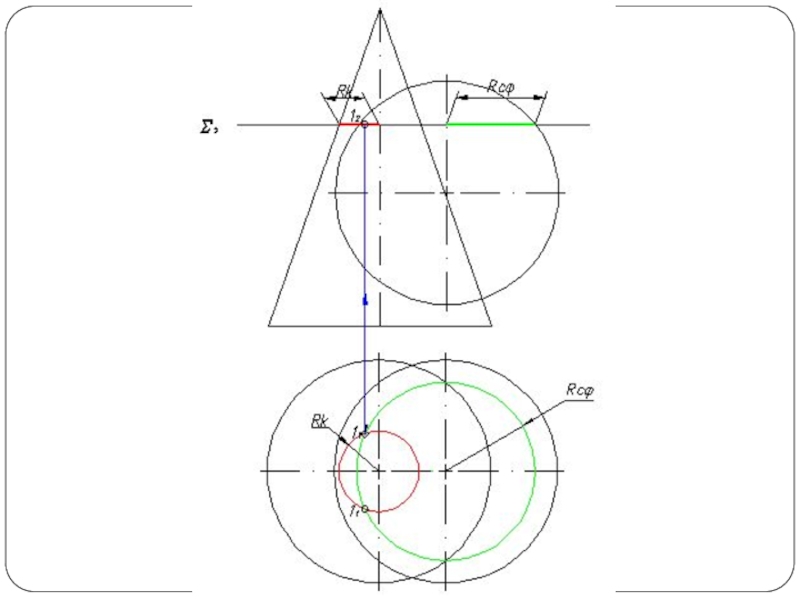
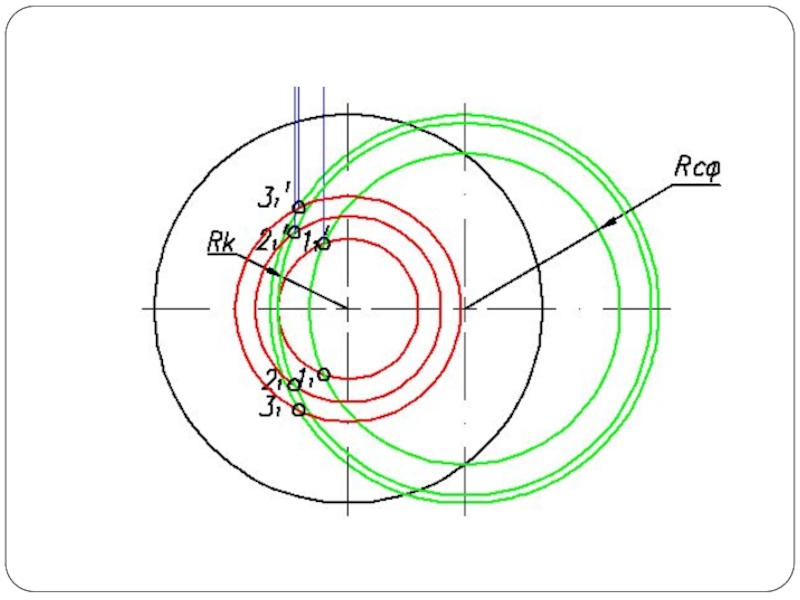
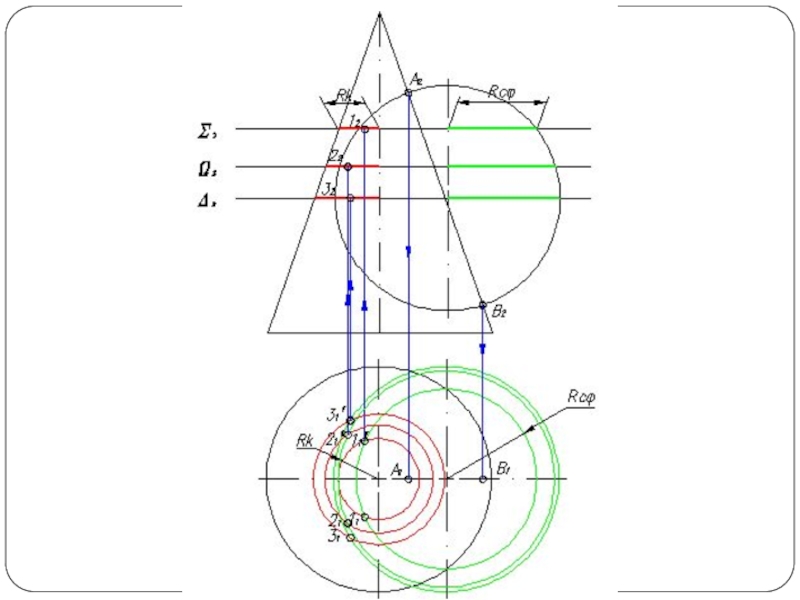
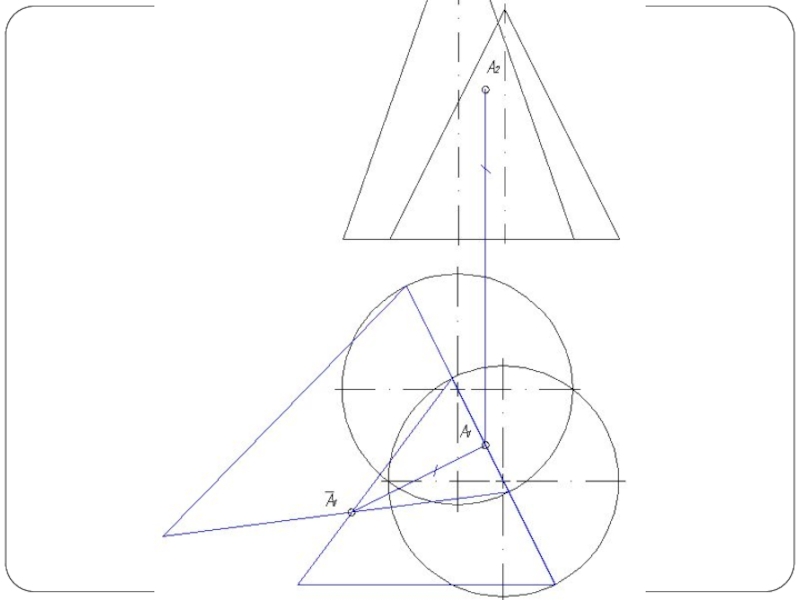
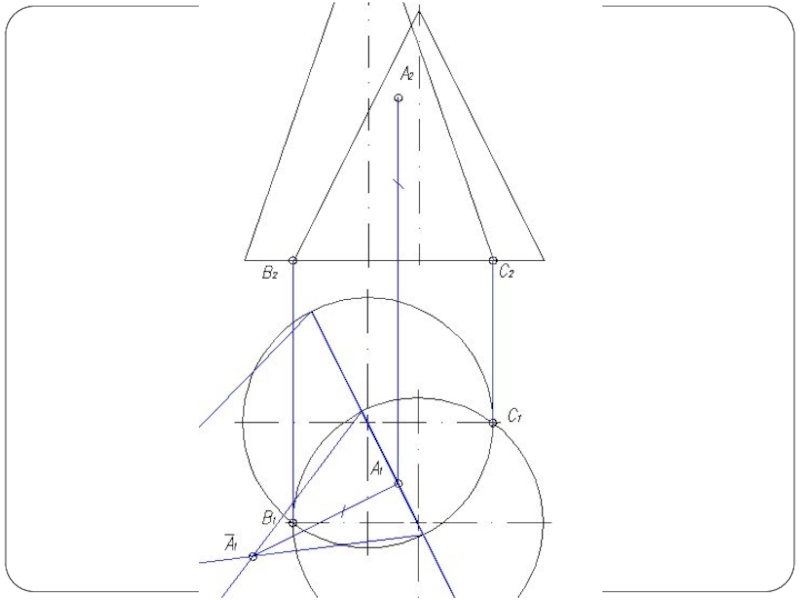
Слайд 2Наиболее общий способ построения линии пересечения двух поверхностей называется способом вспомогательных

секущих поверхностей или способом посредников. Сущность способа заключается в том, что две данные поверхности Φ и Θ (рис. 1а) пересекаются вспомогательными поверхностями или, в частном случае, вспомогательными плоскостями – посредниками. Каждый из посредников пересекает данные поверхности по линиям I и II, лежащим на одной и той же поверхности или в одной и той же плоскости. При взаимном пересечении этих линий получаются общие точки A и В, принадлежащие линии пересечения поверхностей.

Слайд 3

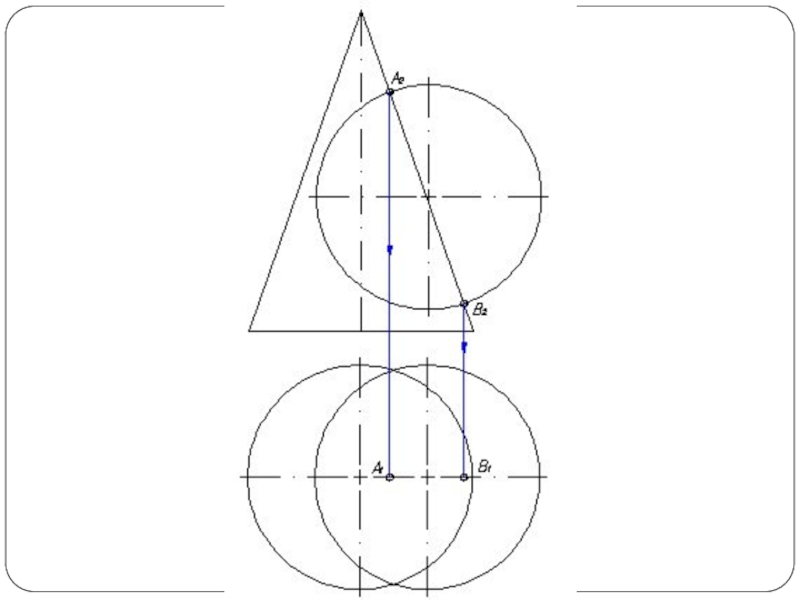
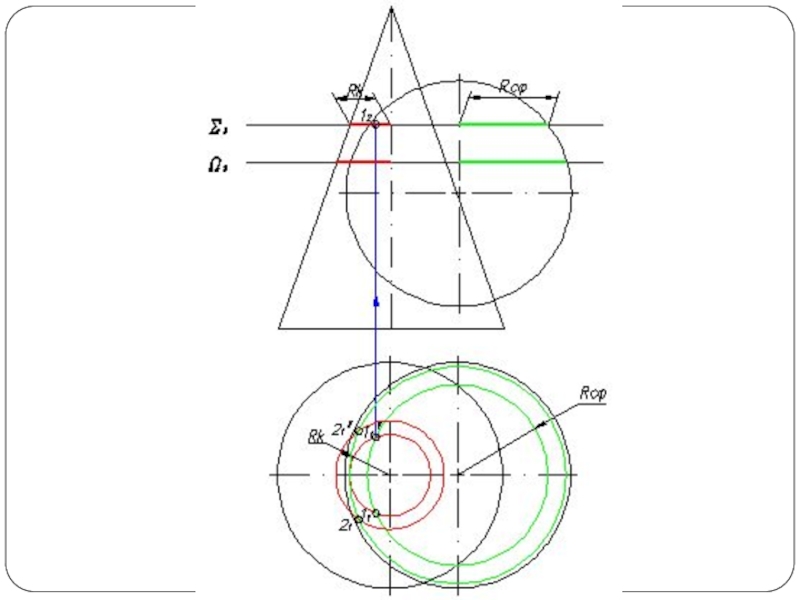
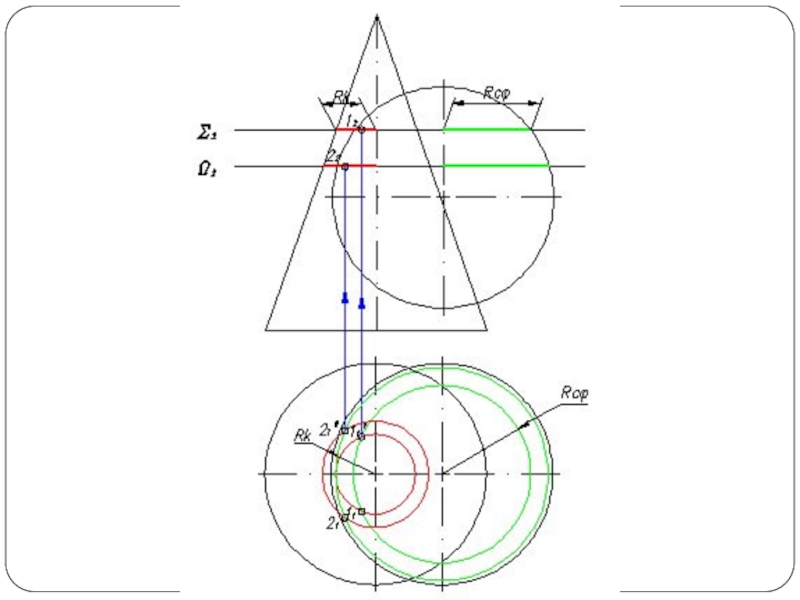
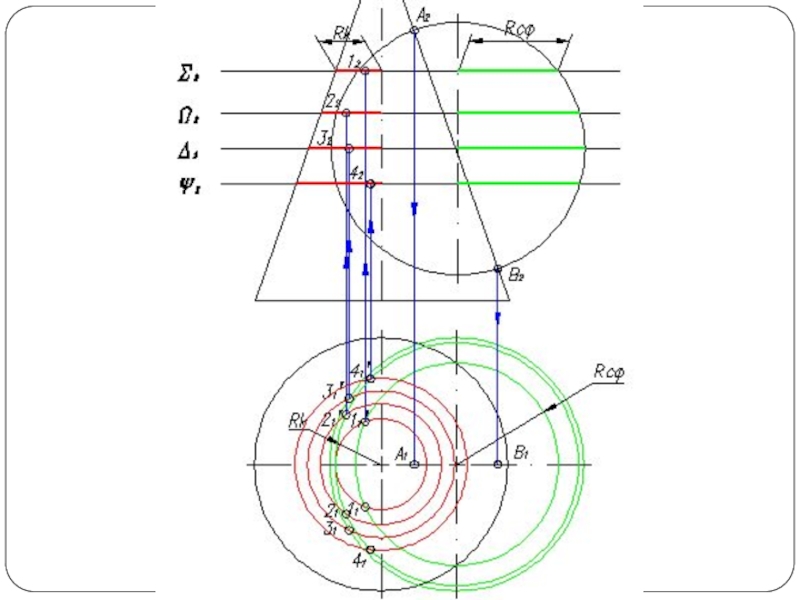
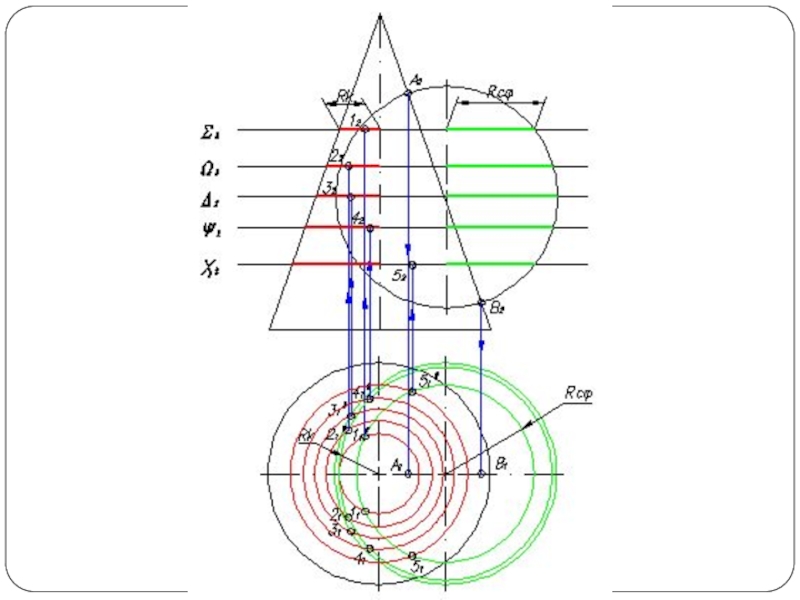
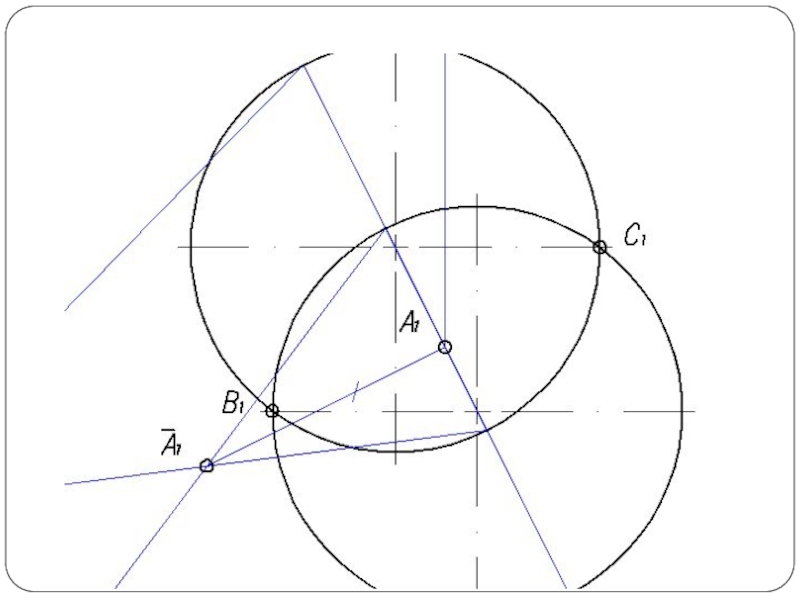
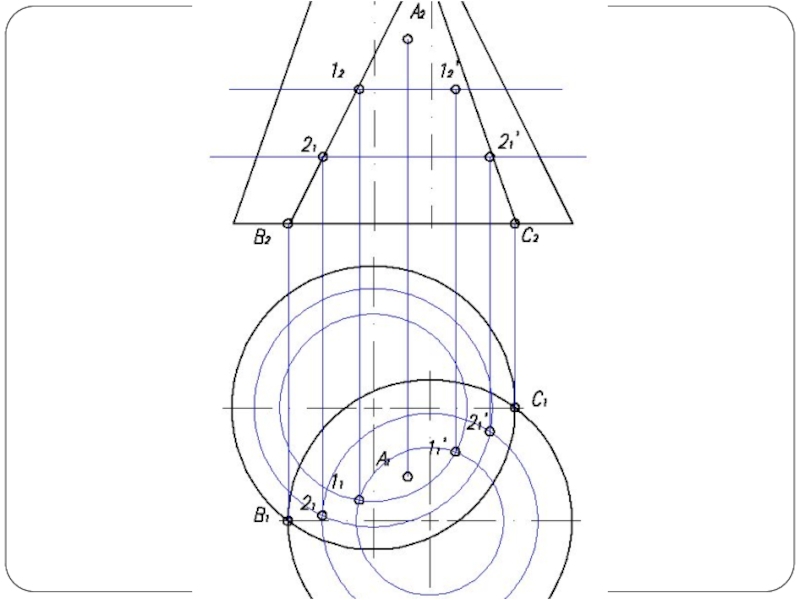
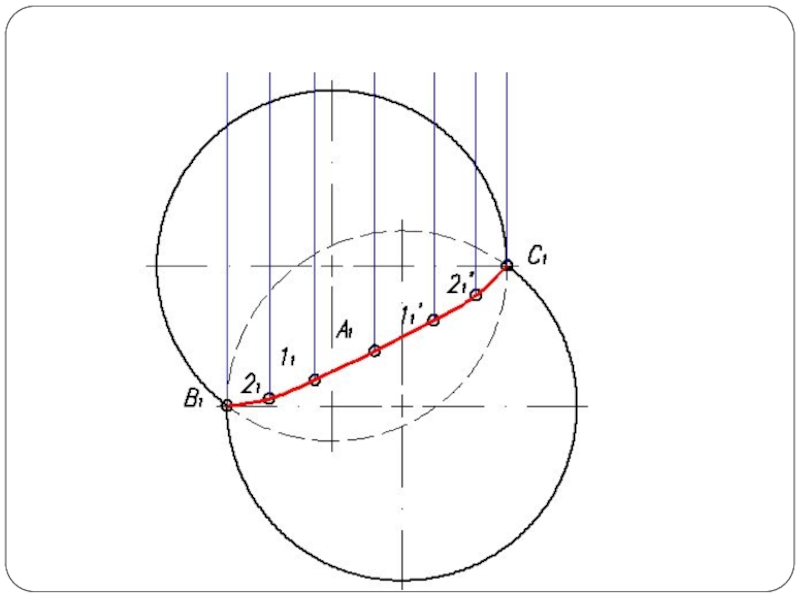
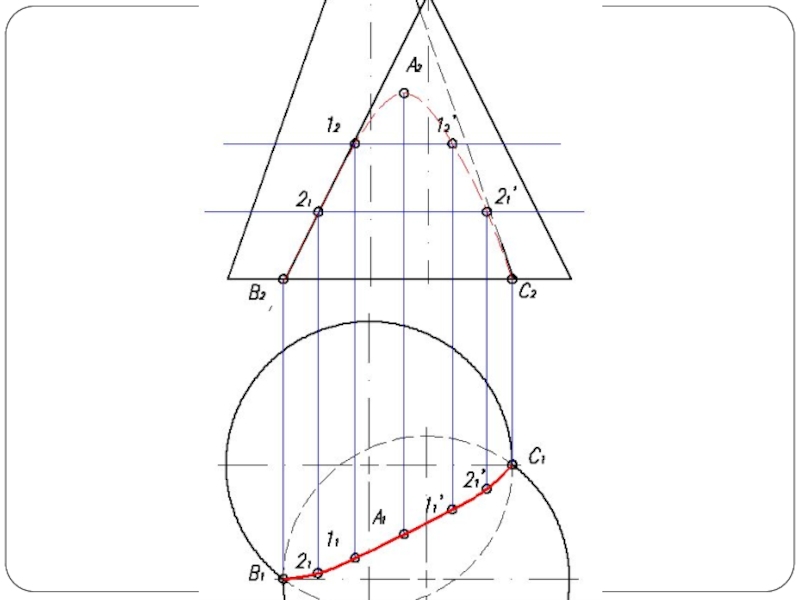
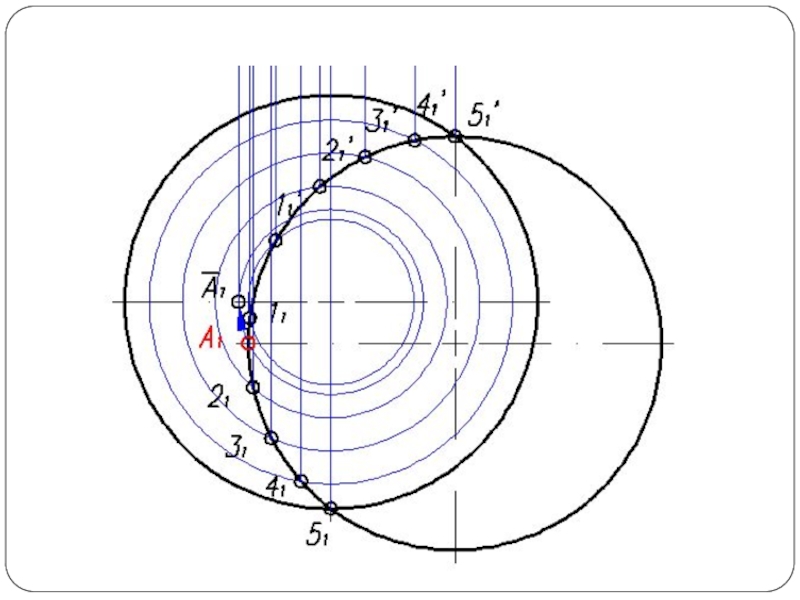
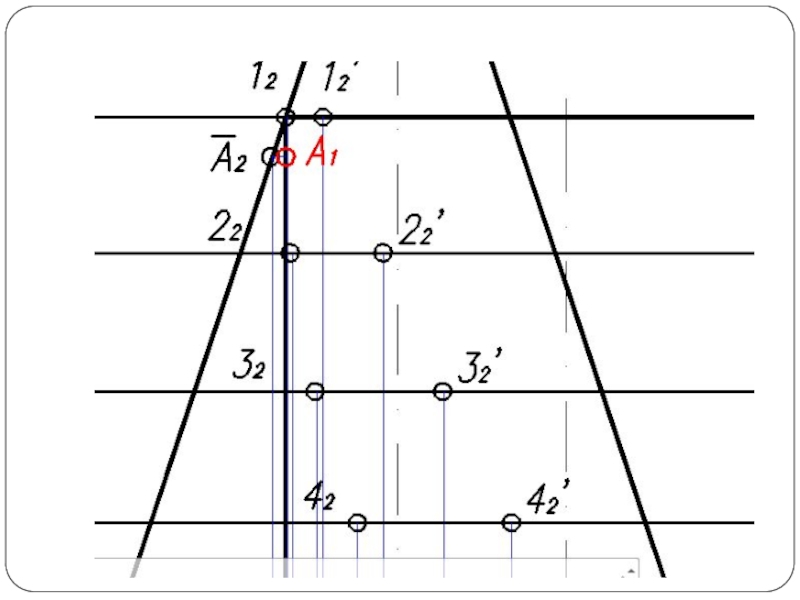
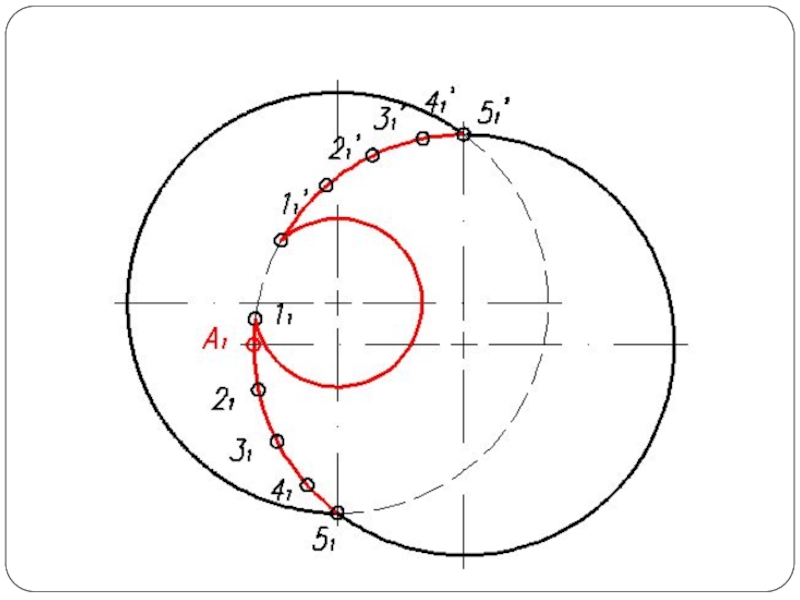
Слайд 4Повторяя указанный прием с различными вспомогательными поверхностями, находят такое количество точек,

которое вполне определяет линию пересечения. Полученные точки соединяют плавной кривой по лекалу.
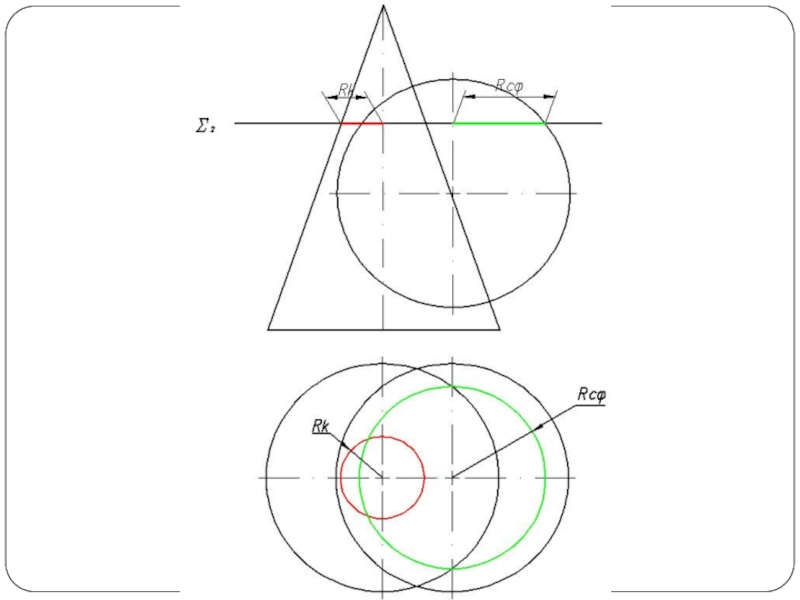
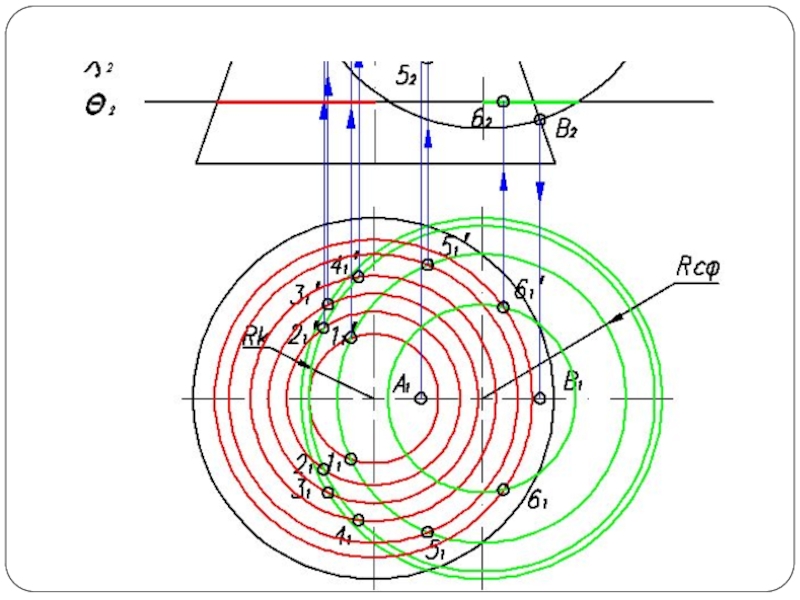
Чаще применяют вспомогательные плоскости частного положения и вспомогательные сферы, при этом следует стремиться к тому, чтобы фигуры сечения поверхностей посредниками по возможности были наиболее простыми — окружностями, прямоугольниками, прямыми линиями (рис. 1б).

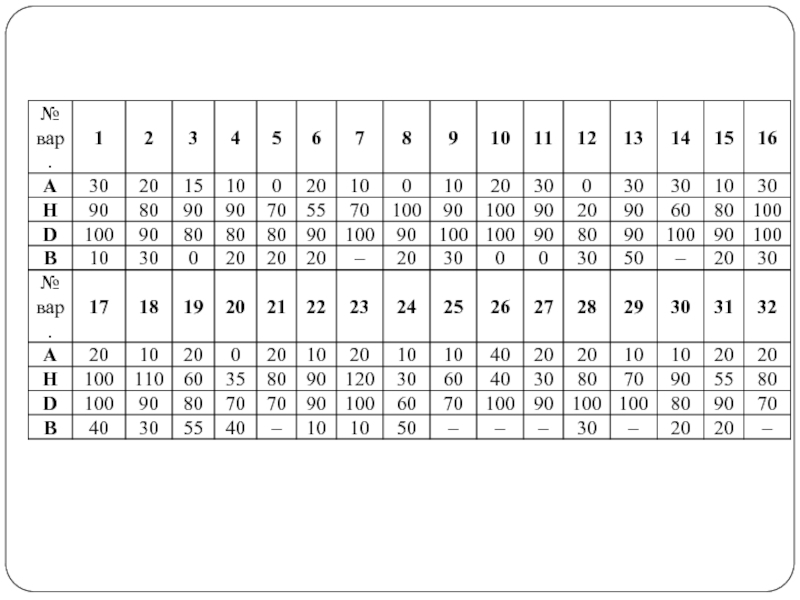
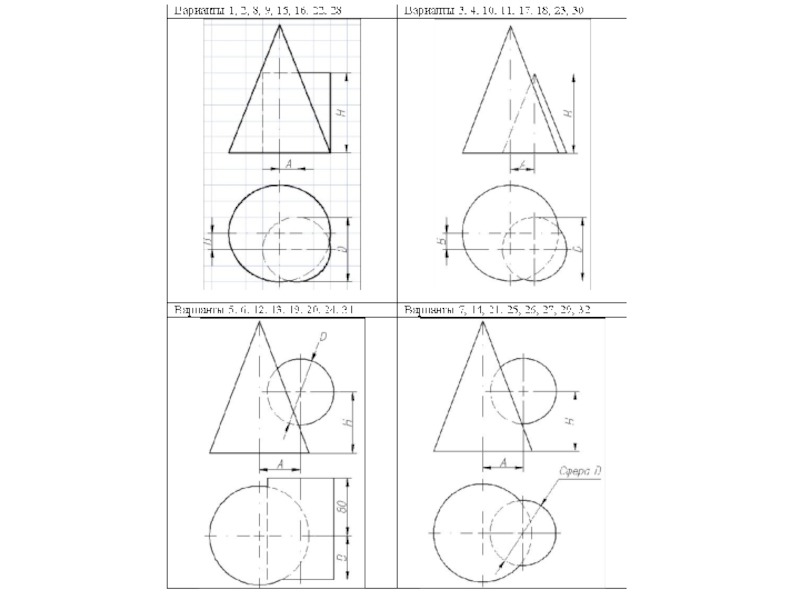
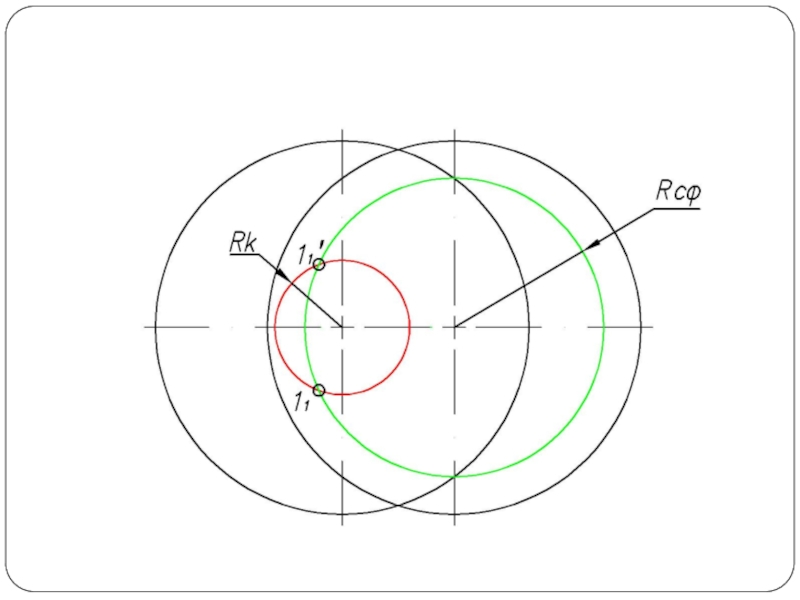
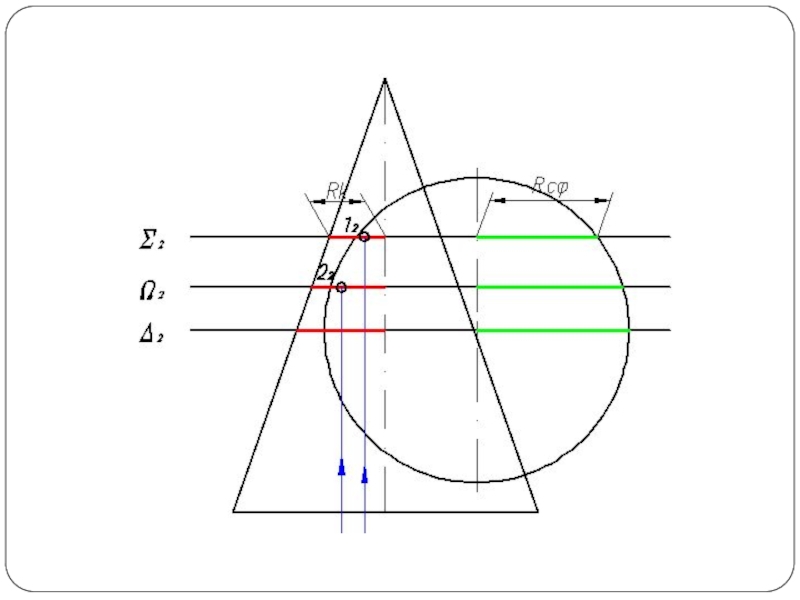
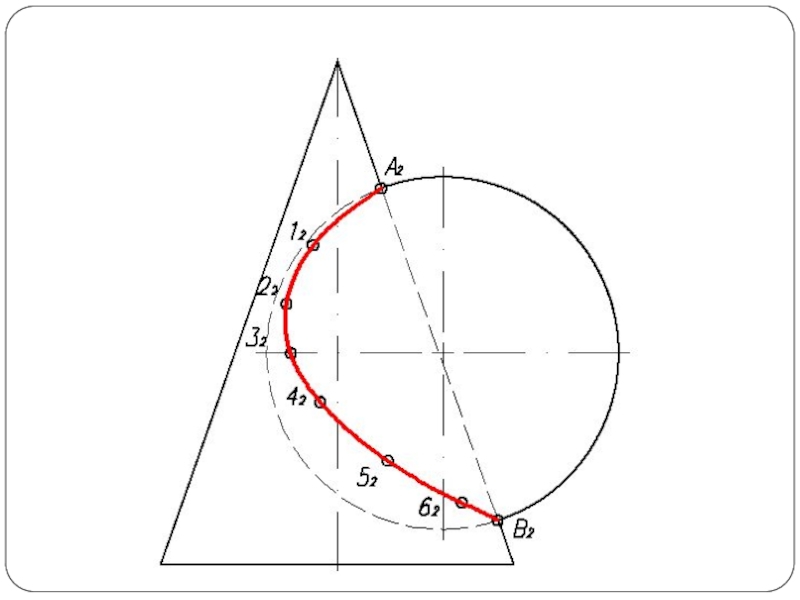
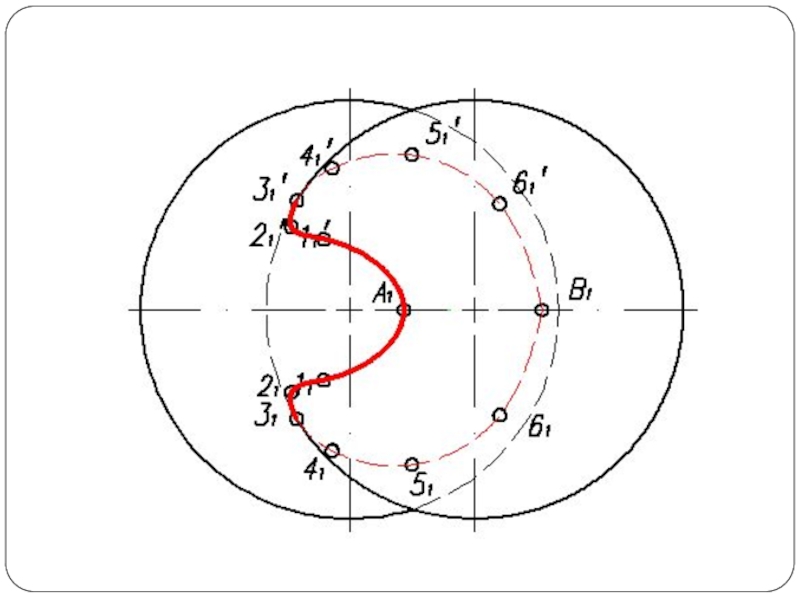
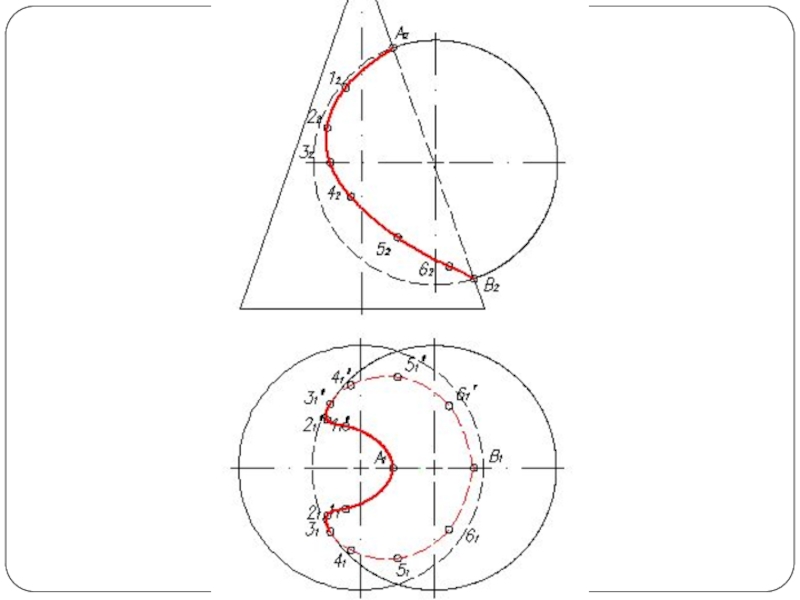
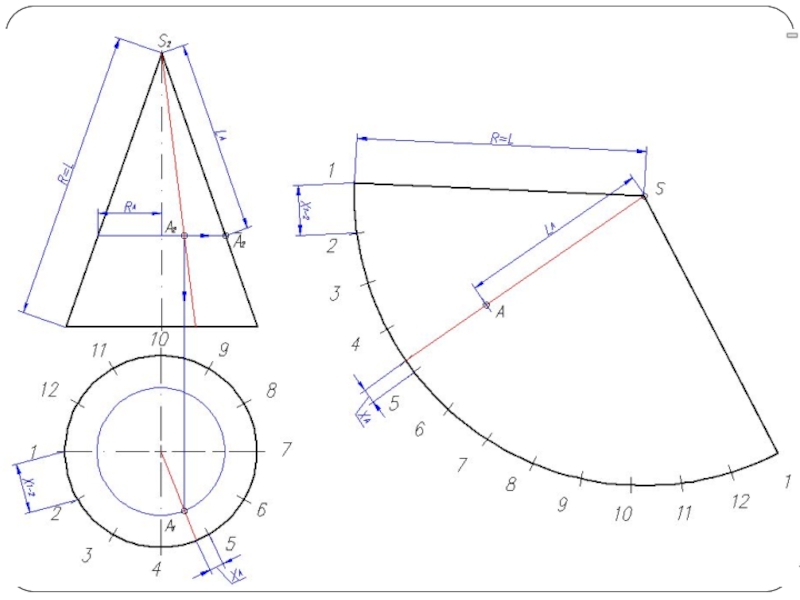
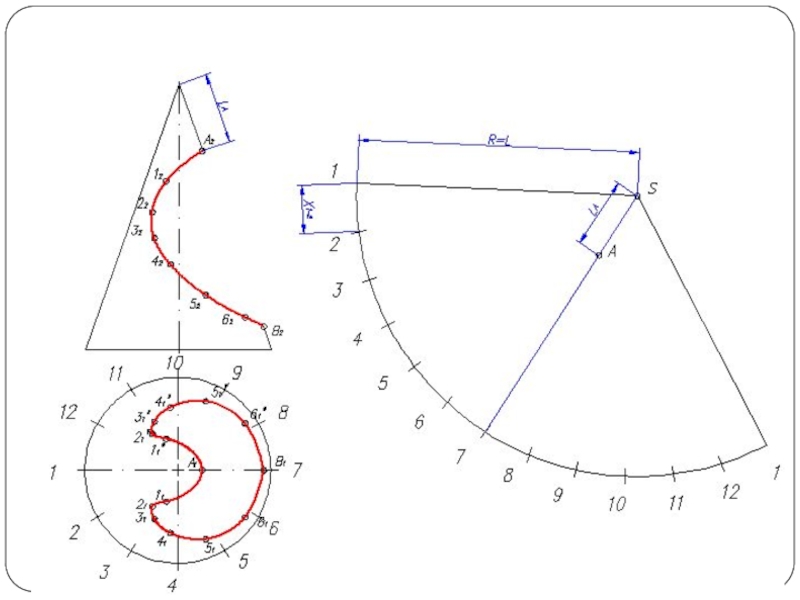
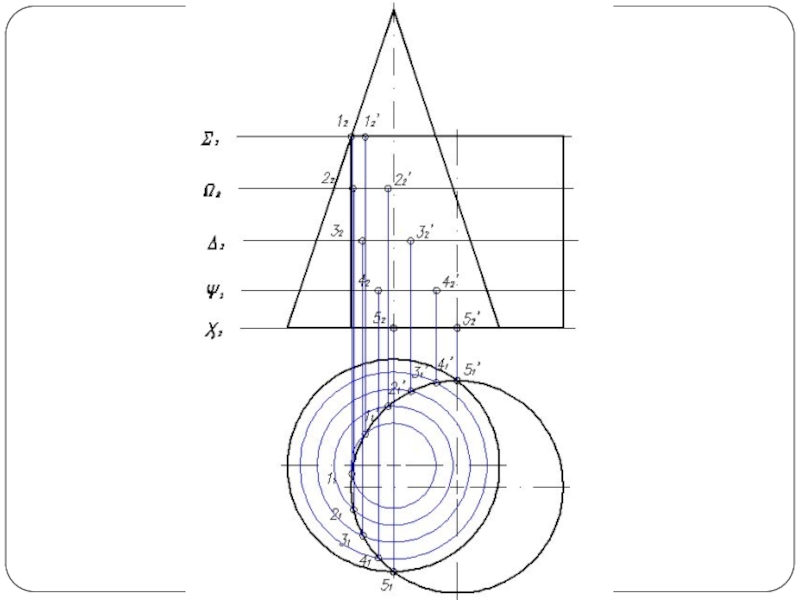
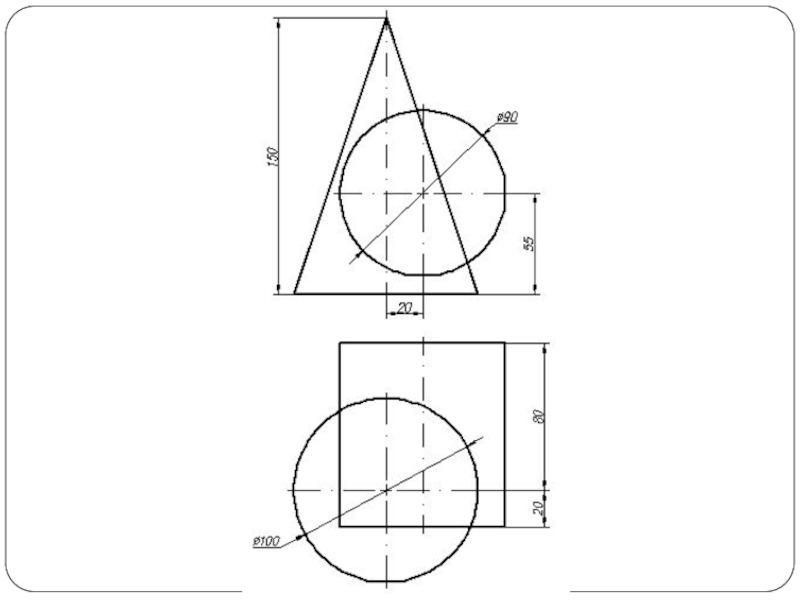
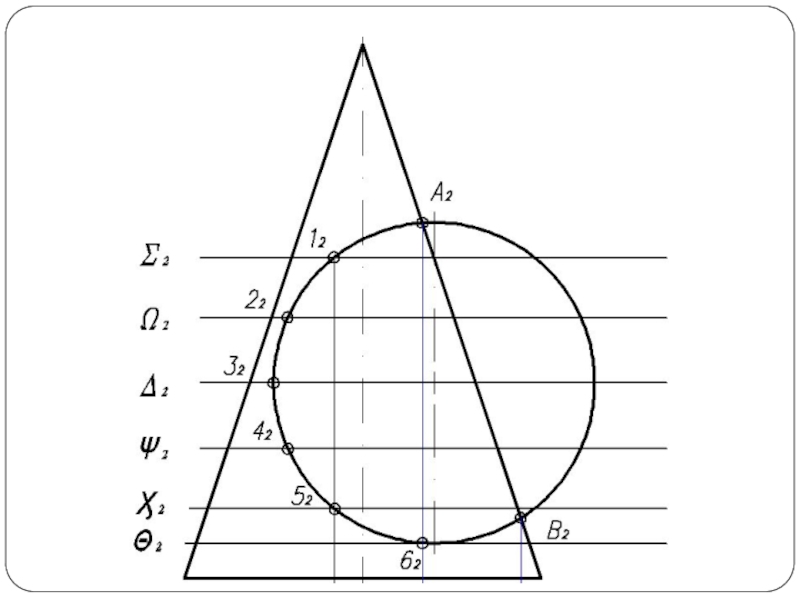
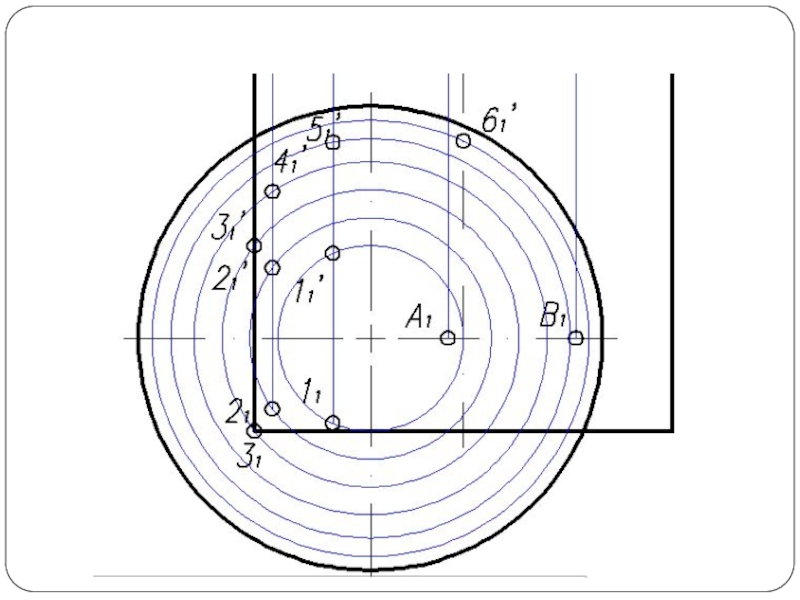
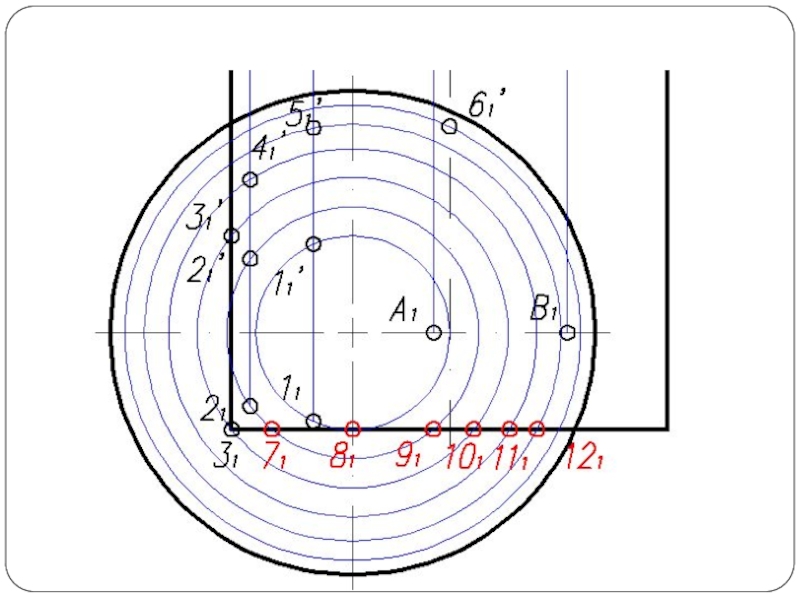
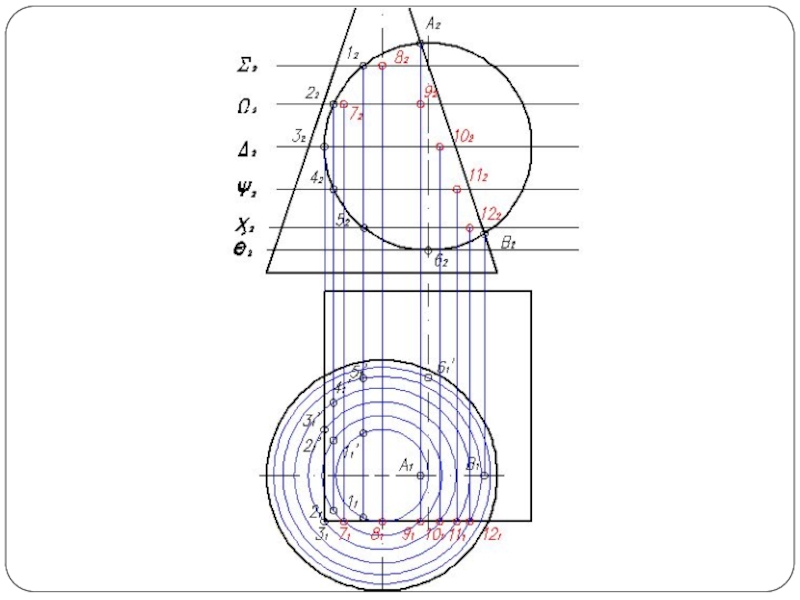
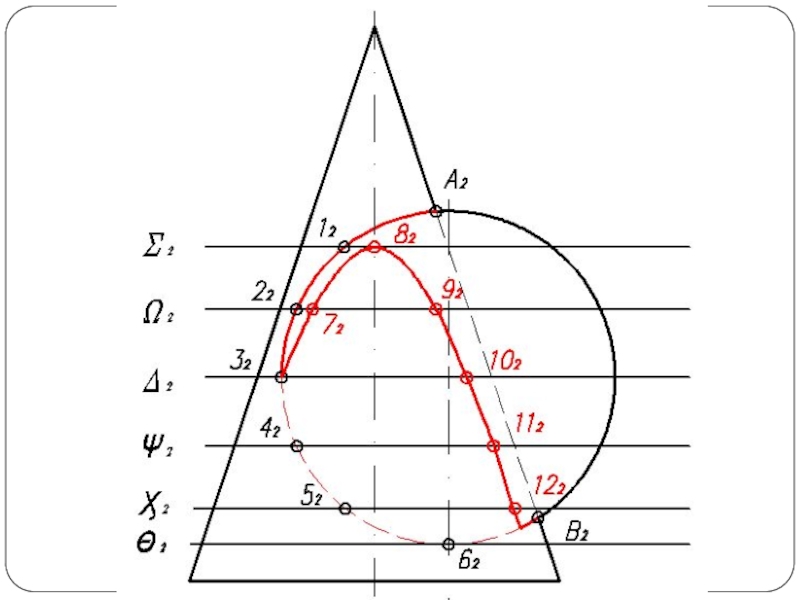
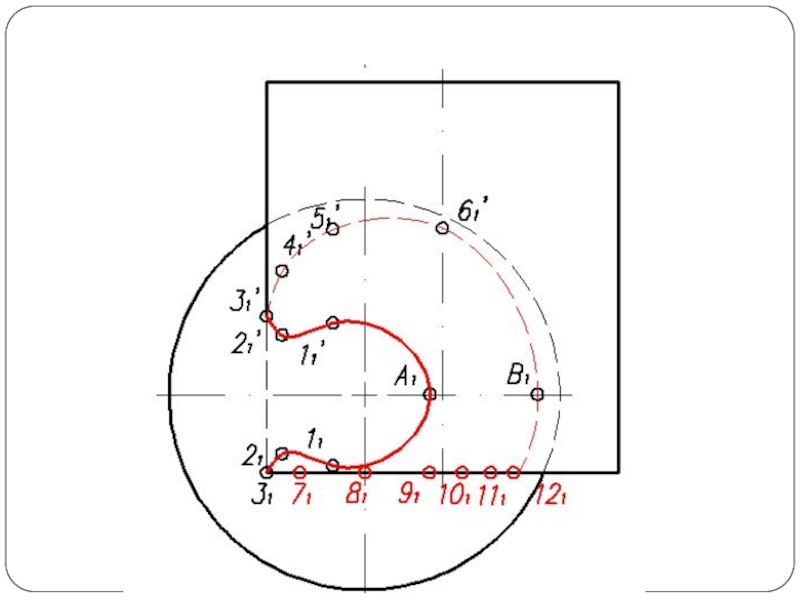
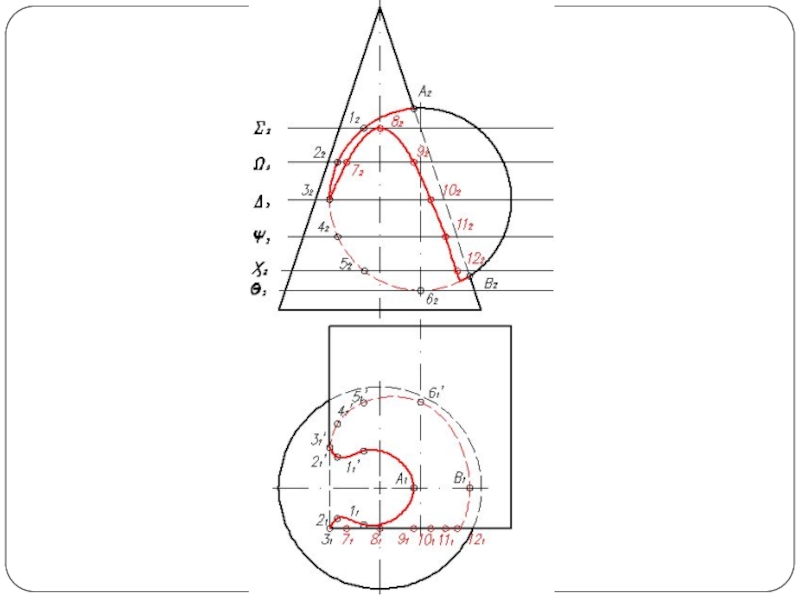
Слайд 5Построить линию пересечения поверхности прямого кругового конуса (диаметр основания – 100

мм, высота – 150 мм) с заданной поверхностью вращения. Определить видимость, вычертить развертку конуса с нанесением линии пересечения. Задание выполнить по вариантам, приведенным в табл. 1.

Слайд 6

Слайд 7

Слайд 8Круговой конус и сфера

Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Слайд 14

Слайд 15

Слайд 16

Слайд 17

Слайд 18

Слайд 19

Слайд 20

Слайд 21

Слайд 22

Слайд 23

Слайд 24

Слайд 25

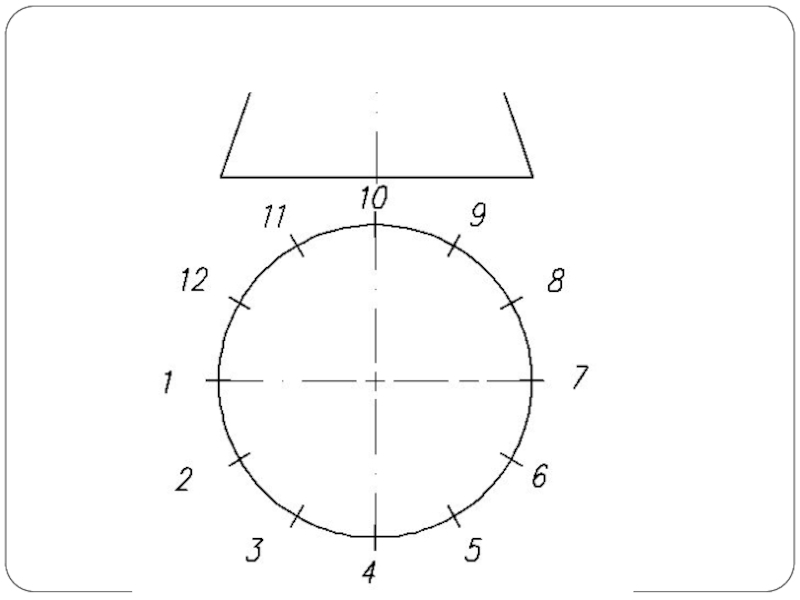
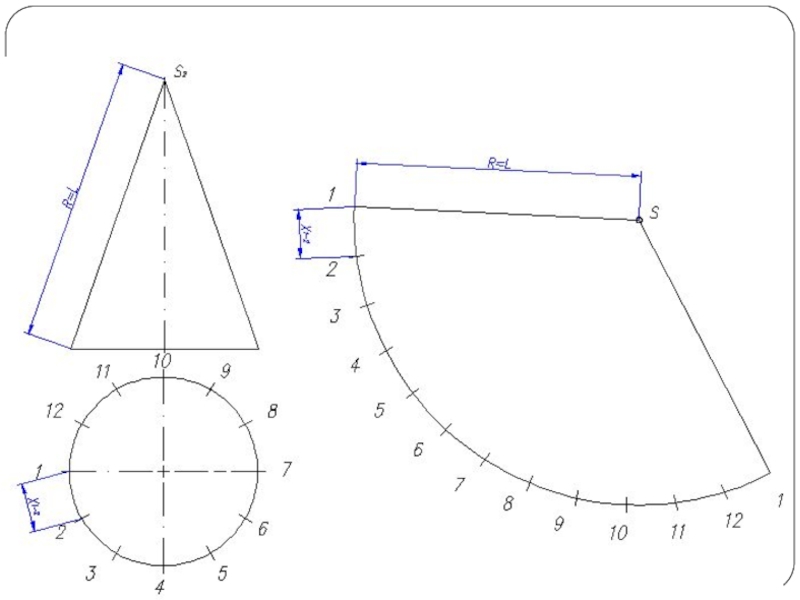
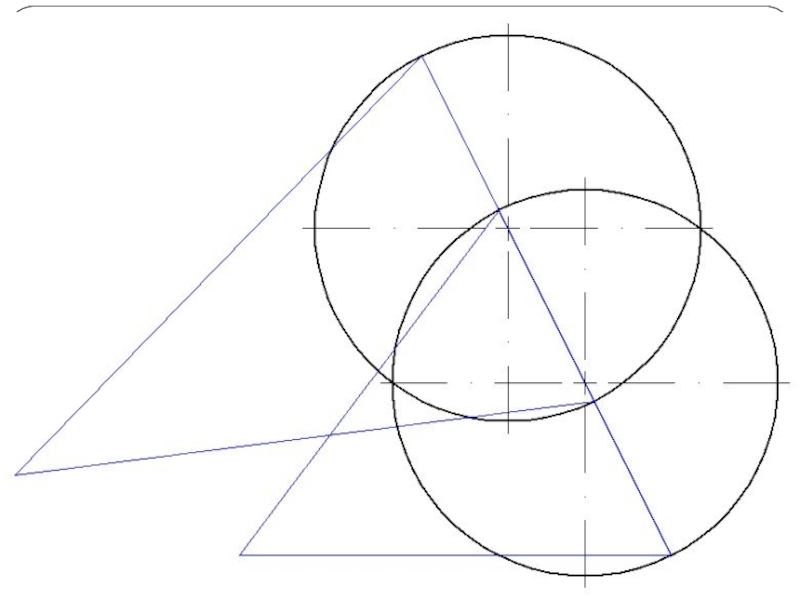
Слайд 26Построение развертки конуса
Разверткой называется плоская фигура, полученная совмещением поверхности тела с

плоскостью.
Основной метод графического построения разверток - это аппроксимация заданной поверхности в виде многогранной поверхности
Часто в поверхность конуса вписывают многогранник с гранями в виде треугольников. Данный способ называется способом триангуляции