- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Электроника, схемотехника, электротехника презентация
Содержание
- 1. Электроника, схемотехника, электротехника
- 2. Последовательное и параллельное соединение элементов электрической цепи
- 3. Параллельным соединением приемников называется такое соединение, при
- 4. При комбинированном соединении элементов можно воспользоваться методом
- 5. Группа резисторов R2, R3, R4 заменяется резистором
- 6. Последовательно включенные источники можно рассматривать как один
- 7. Параллельное включение источников ЭДС на практике
- 11. Условие передачи приёмнику максимальной энергии
- 12. При двух
- 13. Следовательно, некоторому определенному значению соответствует наибольшее возможное
- 14. Такой режим является невыгодным, так как 50
- 15. Пример решения задачи, с цепями постоянного тока
- 16. Отсутствующие значения в таблице принимаем за нуль.
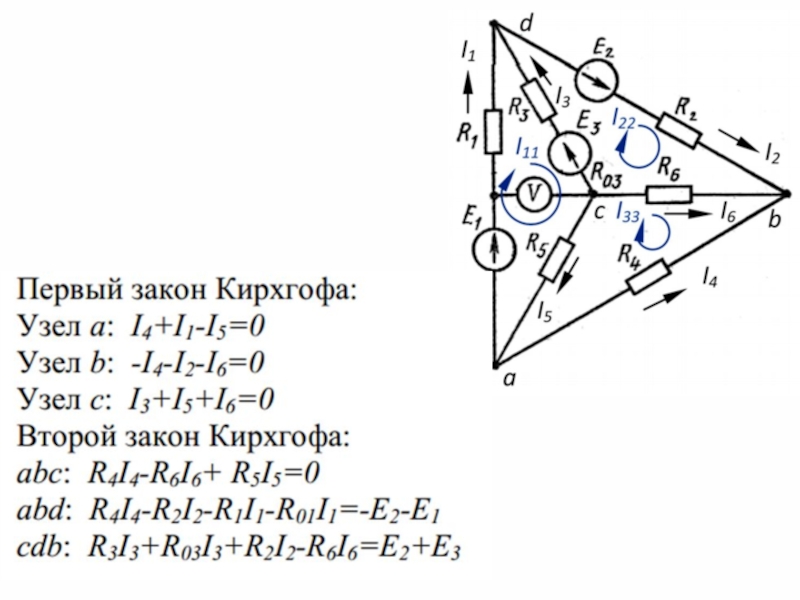
- 17. Далее необходимо написать три уравнения по первому закону и три уравнения по второму закону Кирхгофа.
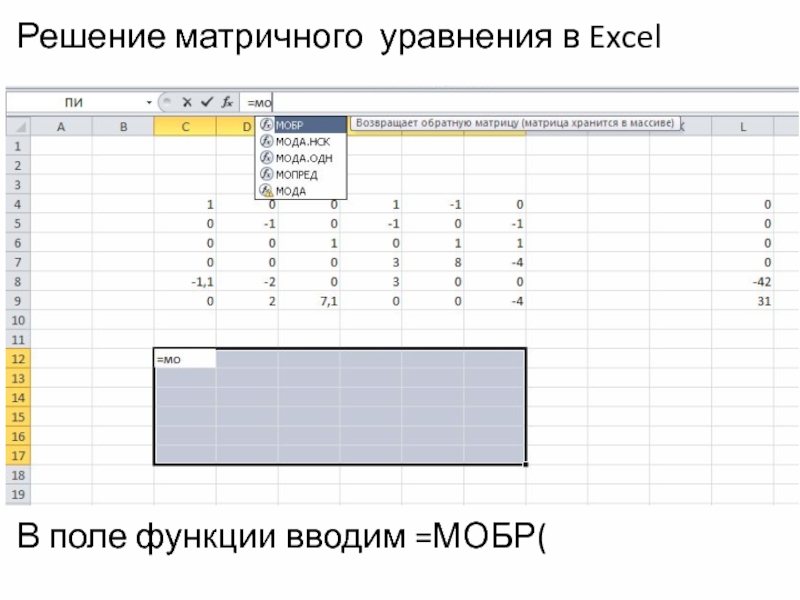
- 20. Решение данного матричного уравнения целесообразно проводить с
- 21. Для баланса мощностей рассчитаем мощность, вырабатываемую источниками
- 22. Решение матричного уравнения в Excel
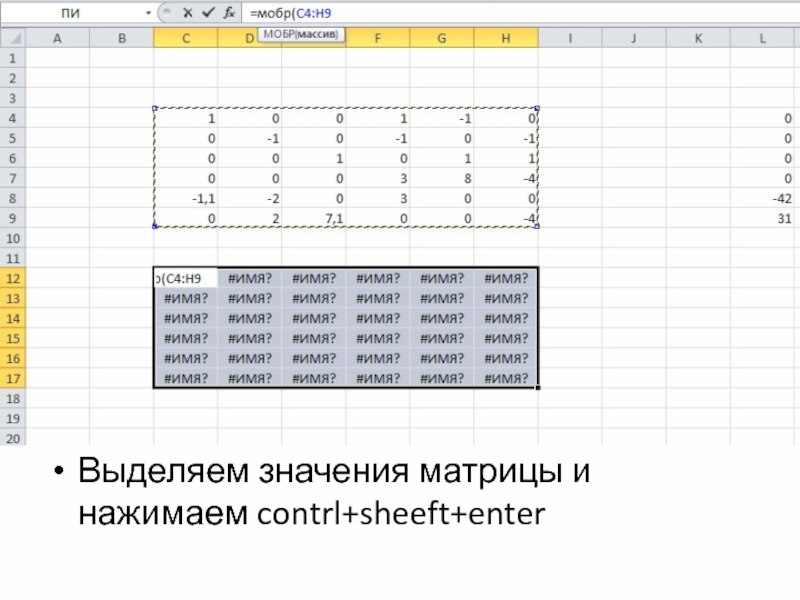
- 23. Выделяем значения матрицы и нажимаем contrl+sheeft+enter
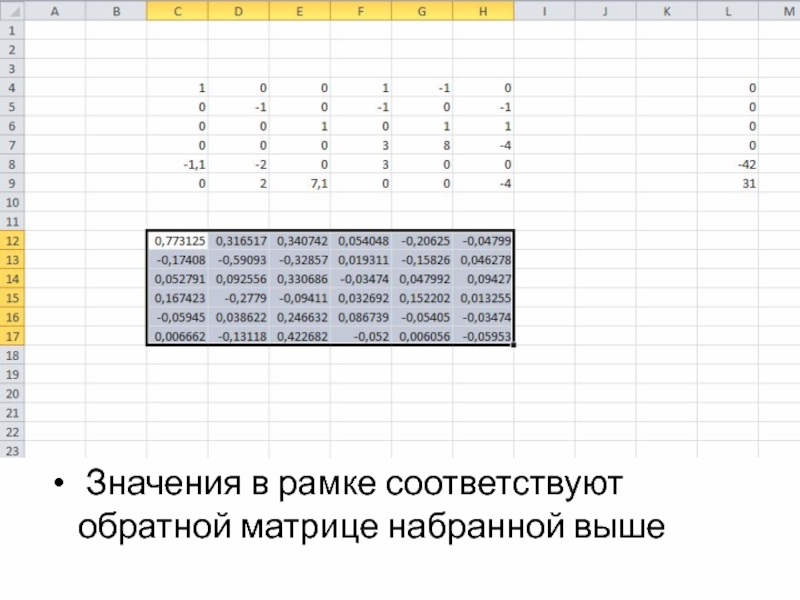
- 24. Значения в рамке соответствуют обратной матрице набранной выше
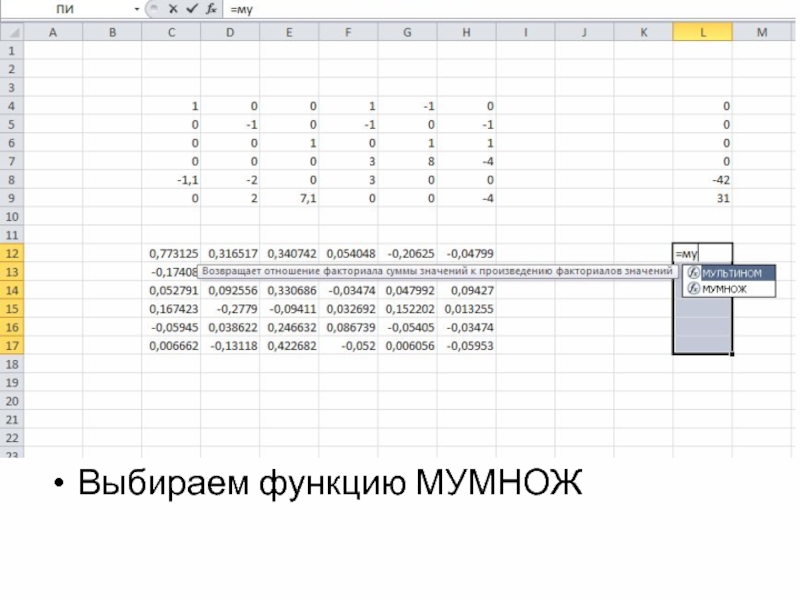
- 25. Выбираем функцию МУМНОЖ
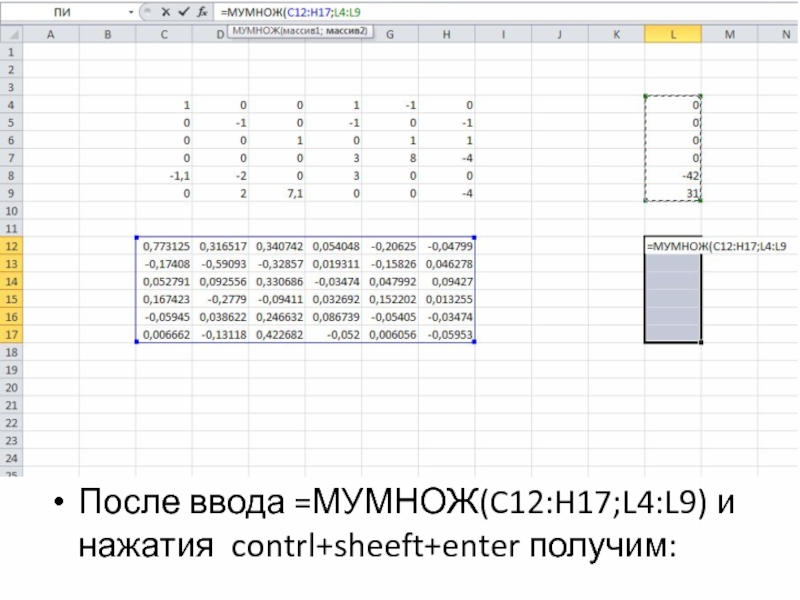
- 26. После ввода =МУМНОЖ(C12:H17;L4:L9) и нажатия contrl+sheeft+enter получим:
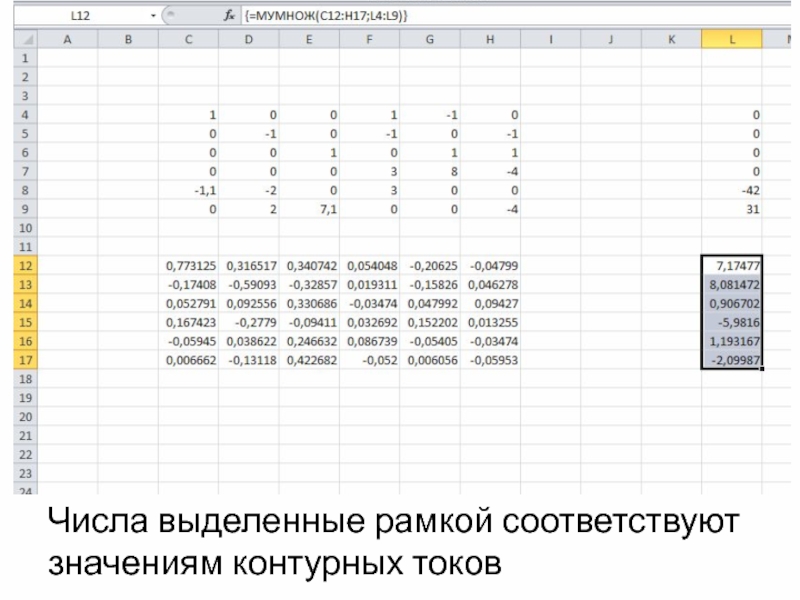
- 27. Числа выделенные рамкой соответствуют значениям контурных токов
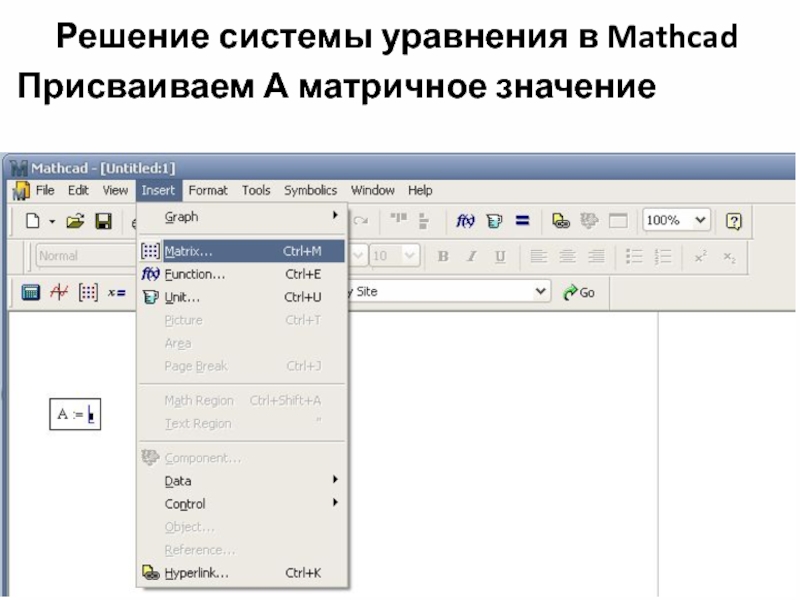
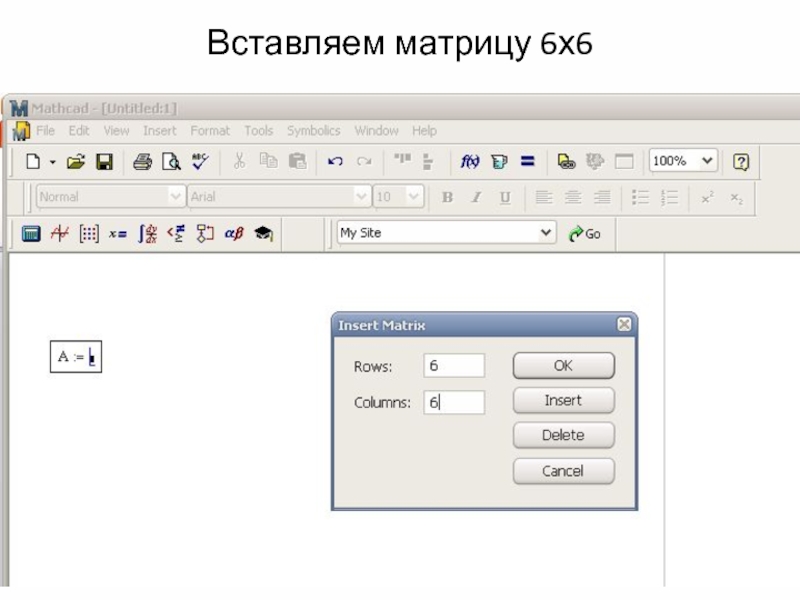
- 28. Решение системы уравнения в Mathcad Присваиваем А матричное значение
- 29. Вставляем матрицу 6х6
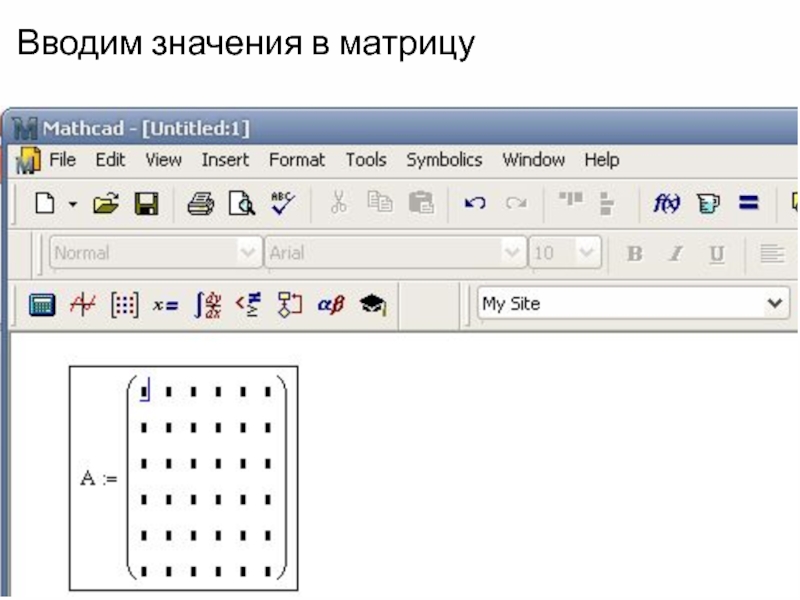
- 30. Вводим значения в матрицу
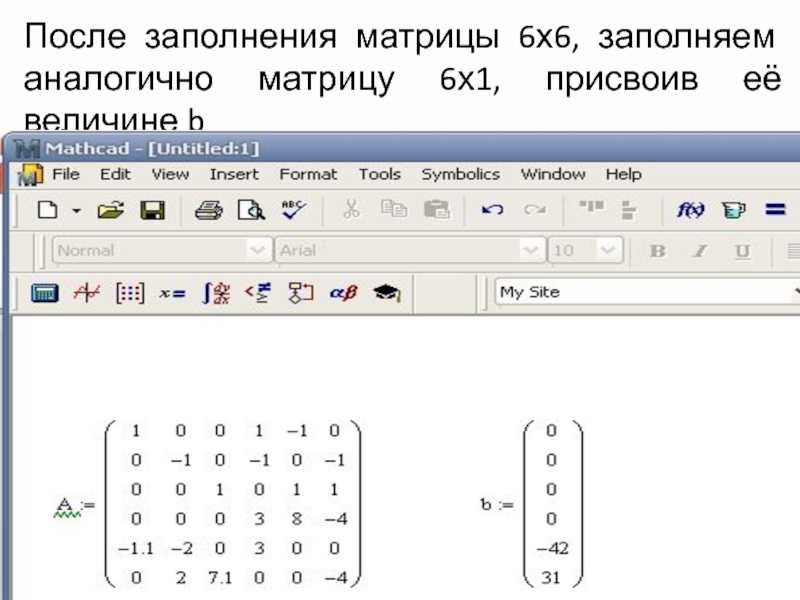
- 31. После заполнения матрицы 6х6, заполняем аналогично матрицу 6х1, присвоив её величине b
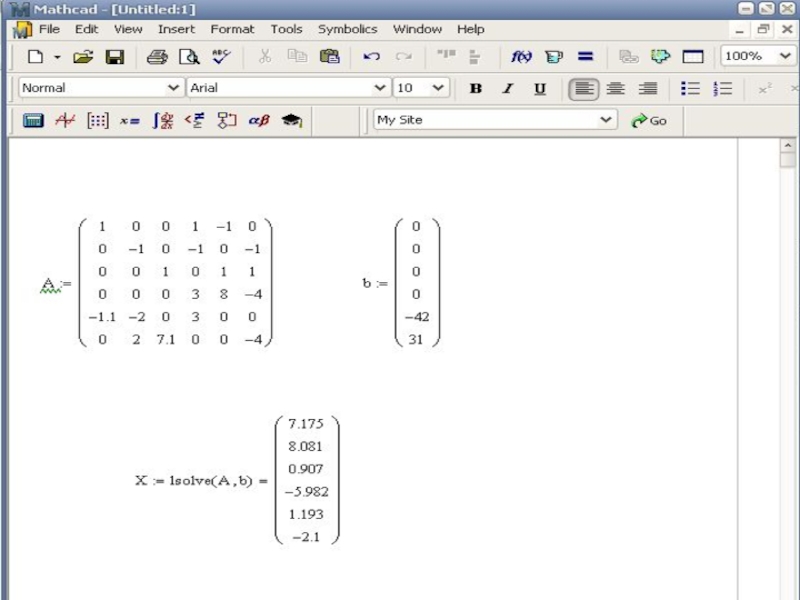
- 32. Для определения токов в контуре, рассмотренного выше,
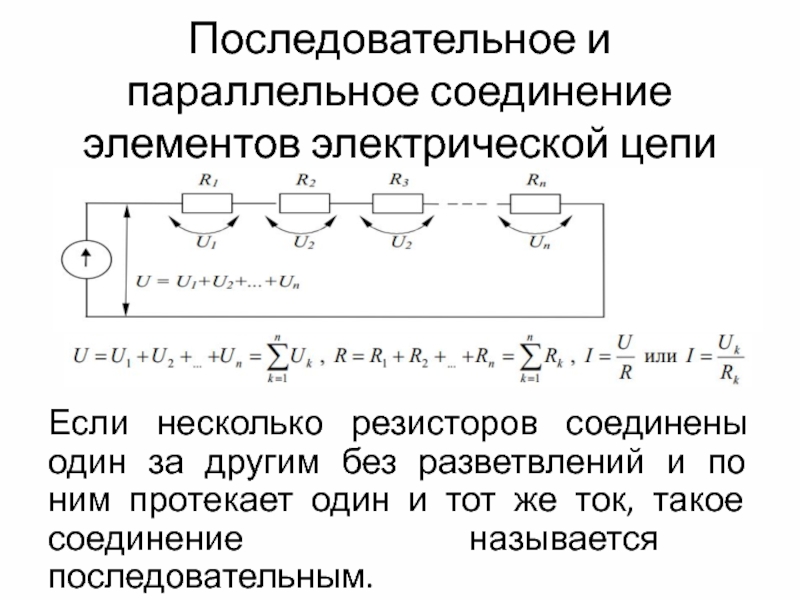
Последовательное и параллельное соединение элементов электрической цепи Если несколько резисторов соединены один за другим без разветвлений и по ним протекает один и тот же ток, такое соединение называется последовательным.
Слайд 2Последовательное и параллельное соединение элементов электрической цепи
Если несколько резисторов соединены один
за другим без разветвлений и по ним протекает один и тот же ток, такое соединение называется последовательным.
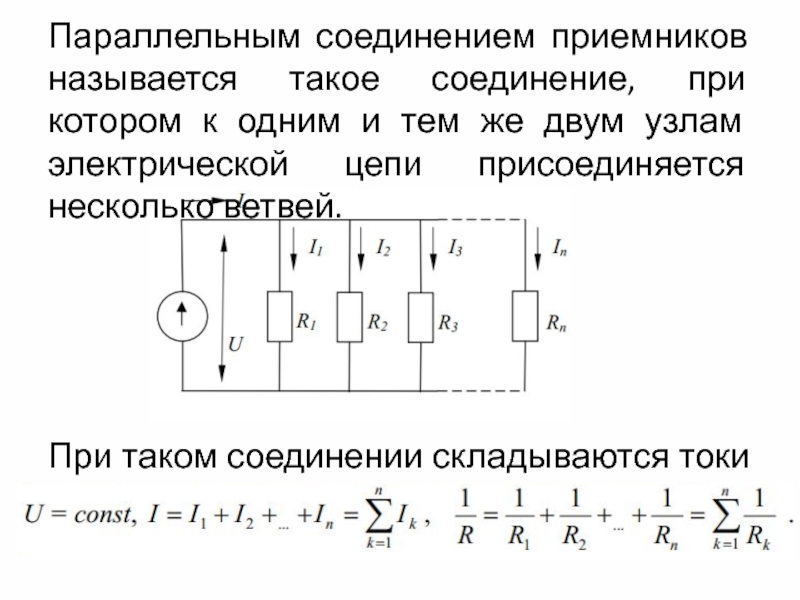
Слайд 3Параллельным соединением приемников называется такое соединение, при котором к одним и
тем же двум узлам электрической цепи присоединяется несколько ветвей.
При таком соединении складываются токи и проводимости:
При таком соединении складываются токи и проводимости:
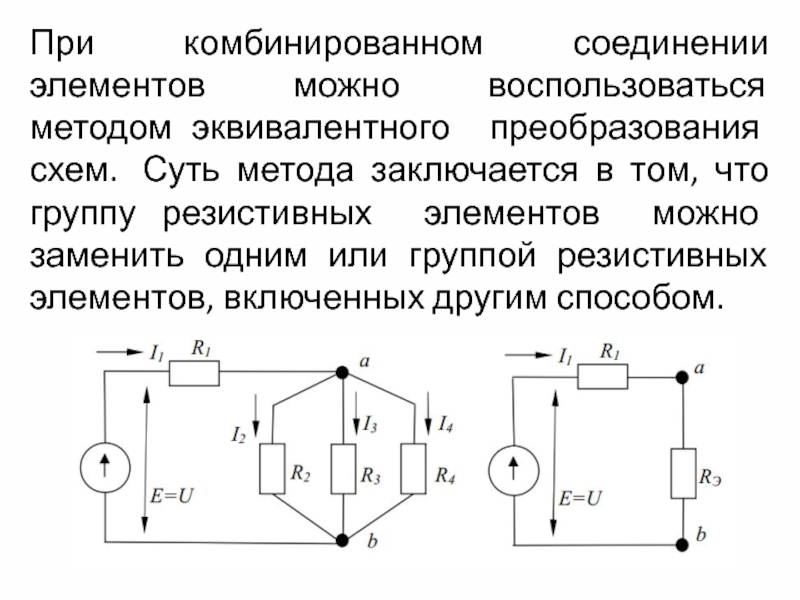
Слайд 4При комбинированном соединении элементов можно воспользоваться методом эквивалентного преобразования схем.
Суть метода заключается в том, что группу резистивных элементов можно заменить одним или группой резистивных элементов, включенных другим способом.
Слайд 5Группа резисторов R2, R3, R4 заменяется резистором с эквивалентным сопротивлением
что не
изменяет общего тока в цепи. Общее сопротивление цепи может быть найдено как
Общий ток в цепи определится как I1=E/R, напряжение Uab=I1Rэ, а токи I2=Uab/R2, I3=Uab/R3, I4=Uab/R4
Общий ток в цепи определится как I1=E/R, напряжение Uab=I1Rэ, а токи I2=Uab/R2, I3=Uab/R3, I4=Uab/R4
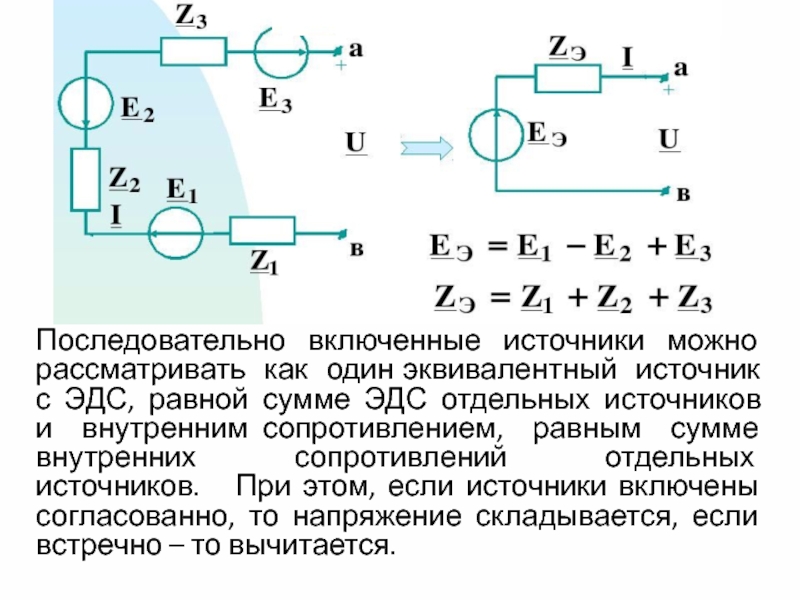
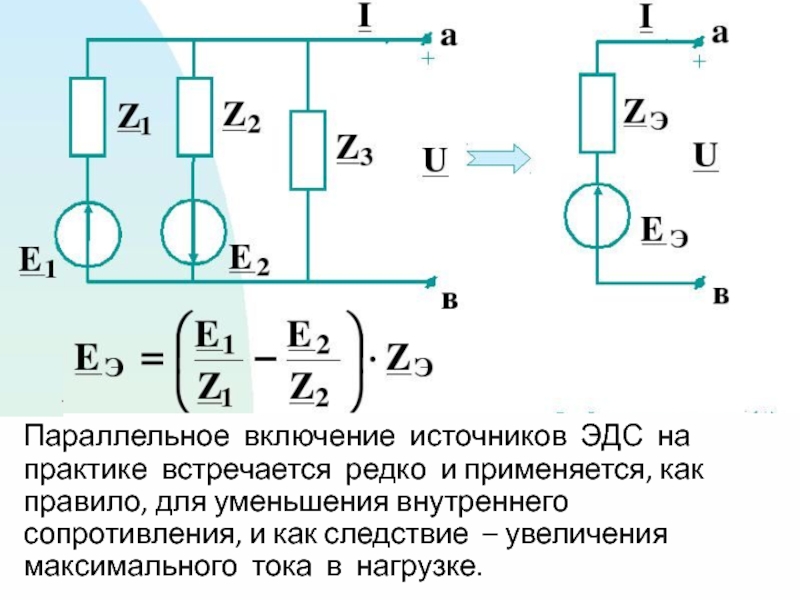
Слайд 6Последовательно включенные источники можно рассматривать как один эквивалентный источник с ЭДС,
равной сумме ЭДС отдельных источников и внутренним сопротивлением, равным сумме внутренних сопротивлений отдельных источников. При этом, если источники включены согласованно, то напряжение складывается, если встречно – то вычитается.
Слайд 7
Параллельное включение источников ЭДС на практике встречается редко и применяется, как
правило, для уменьшения внутреннего сопротивления, и как следствие – увеличения максимального тока в нагрузке.
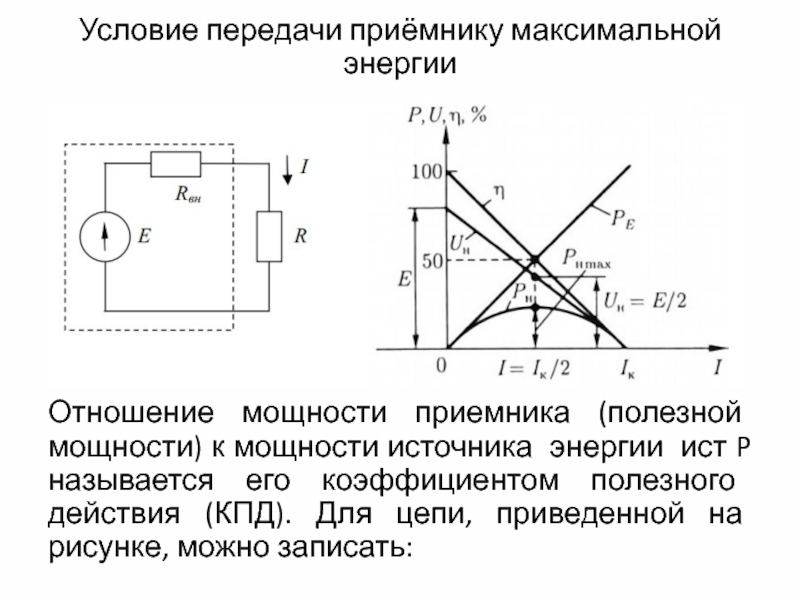
Слайд 11Условие передачи приёмнику максимальной энергии
Отношение мощности приемника (полезной мощности) к мощности
источника энергии ист P называется его коэффициентом полезного действия (КПД). Для цепи, приведенной на рисунке, можно записать:
Слайд 12
При двух предельных значениях опротивления R = 0 и R стремящемся
к бесконечности, мощность приемника равна нулю, так как в первом случае равно нулю напряжение между выводами приемника, а во втором случае — ток в цепи.
Слайд 13Следовательно, некоторому определенному значению соответствует наибольшее возможное (при данных Е и
Rвн) значение мощности приемника. Чтобы определить это значение сопротивления, достаточно приравнять нулю первую производную от мощности Р по R. При этом получается, что максимум мощности передается в нагрузку при R=Rвн. Таким образом, источник ЭДС развивает максимальную полезную мощность, когда внешнее сопротивление равно внутреннему сопротивлению источника, при этом мощность будет равна:
Слайд 14Такой режим является невыгодным, так как 50 % энергии теряется во
внутреннем сопротивлении источника
Режим цепи, при котором внешнее сопротивление цепи равно внутреннему
сопротивлению источника энергии, называется режимом согласованной нагрузки.
Режим цепи, при котором внешнее сопротивление цепи равно внутреннему
сопротивлению источника энергии, называется режимом согласованной нагрузки.
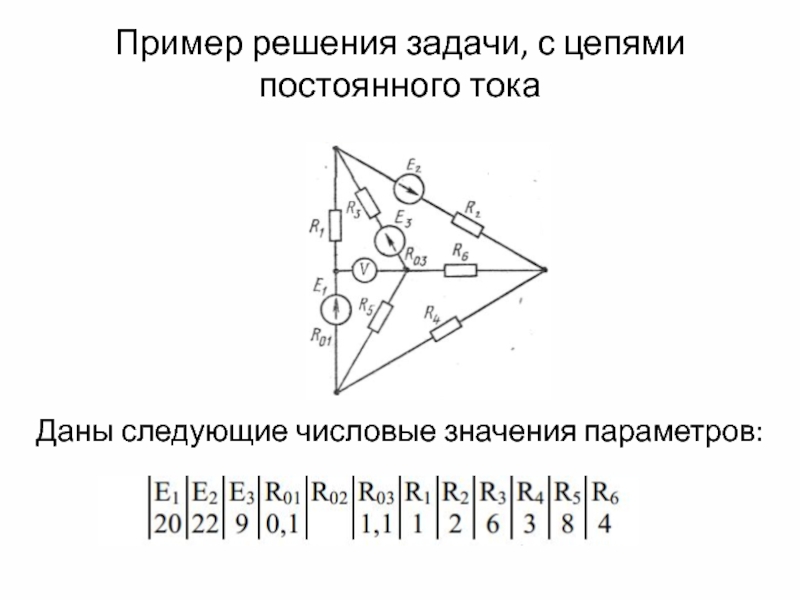
Слайд 15Пример решения задачи, с цепями постоянного тока
Даны следующие числовые значения параметров:
Слайд 16Отсутствующие значения в таблице принимаем за нуль.
Для приведенной выше схемы
необходимо найти:
1. токи во всех ветвях с помощью законов Кирхгофа;
2. составить баланс мощностей;
определить показания вольтметра
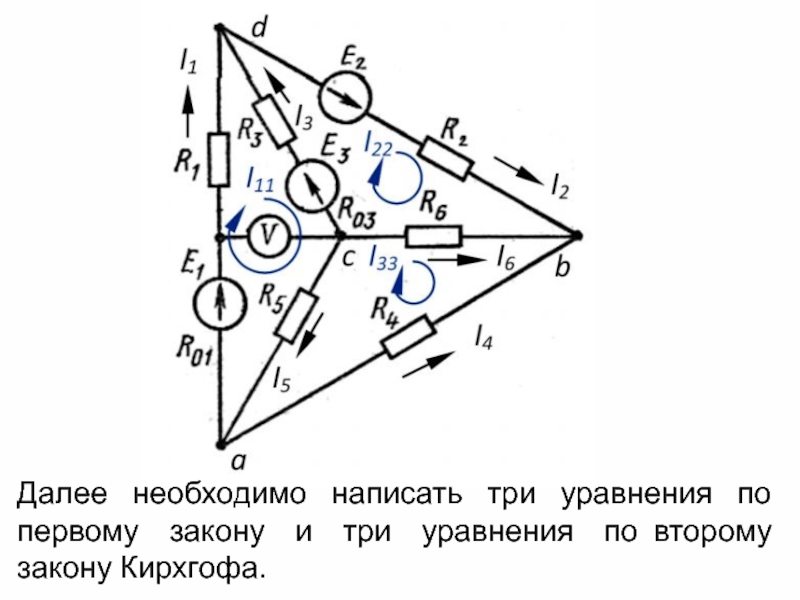
Для составления уравнений по законам Кирхгофа необходимо выбрать направления токов и отметить узлы схемы. Направления токов выбираются произвольным образом.
1. токи во всех ветвях с помощью законов Кирхгофа;
2. составить баланс мощностей;
определить показания вольтметра
Для составления уравнений по законам Кирхгофа необходимо выбрать направления токов и отметить узлы схемы. Направления токов выбираются произвольным образом.
Слайд 17Далее необходимо написать три уравнения по первому закону и три уравнения
по второму закону Кирхгофа.
Слайд 20Решение данного матричного уравнения целесообразно проводить с помощью персонального компьютера. Подставив
числа, получим:
Знак «минус» у токов I4 и I6 означают, что они протекают в направлении, противоположном выбранному.
Знак «минус» у токов I4 и I6 означают, что они протекают в направлении, противоположном выбранному.
Слайд 21Для баланса мощностей рассчитаем мощность, вырабатываемую источниками ЭДС:
Мощность на приемниках энергии
составит:
Напряжение на вольтметре вычисляем по второму закону Кирхгофа, для чего можно
представить вольтметр как источник ЭДС с напряжением V. Тогда:
Знак «минус» означает, что напряжение противоположно выбранному обходу контура,
т.е. плюс вольтметра будет слева по схеме.
Напряжение на вольтметре вычисляем по второму закону Кирхгофа, для чего можно
представить вольтметр как источник ЭДС с напряжением V. Тогда:
Знак «минус» означает, что напряжение противоположно выбранному обходу контура,
т.е. плюс вольтметра будет слева по схеме.