- Главная
- Разное
- Дизайн
- Бизнес и предпринимательство
- Аналитика
- Образование
- Развлечения
- Красота и здоровье
- Финансы
- Государство
- Путешествия
- Спорт
- Недвижимость
- Армия
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ДИНАМИКА ОБЩЕСТВЕННЫХ ЯВЛЕНИЙ презентация
Содержание
- 1. ДИНАМИКА ОБЩЕСТВЕННЫХ ЯВЛЕНИЙ
- 2. это последовательность упорядоченных во времени числовых
- 4. Примеры рядов динамики Число дошкольных учреждений в
- 5. Примеры рядов динамики Моментный Относительных
- 6. Примеры рядов динамики Интервальный Средних
- 7. Сопоставимость по территории Сопоставимость
- 8. Показатели анализа рядов динамики
- 9. Показатели анализа рядов динамики
- 10. средний уровень ряда - показатель, обобщающий
- 11. Средний уровень ряда Для интервальных рядов
- 12. Средний абсолютный прирост
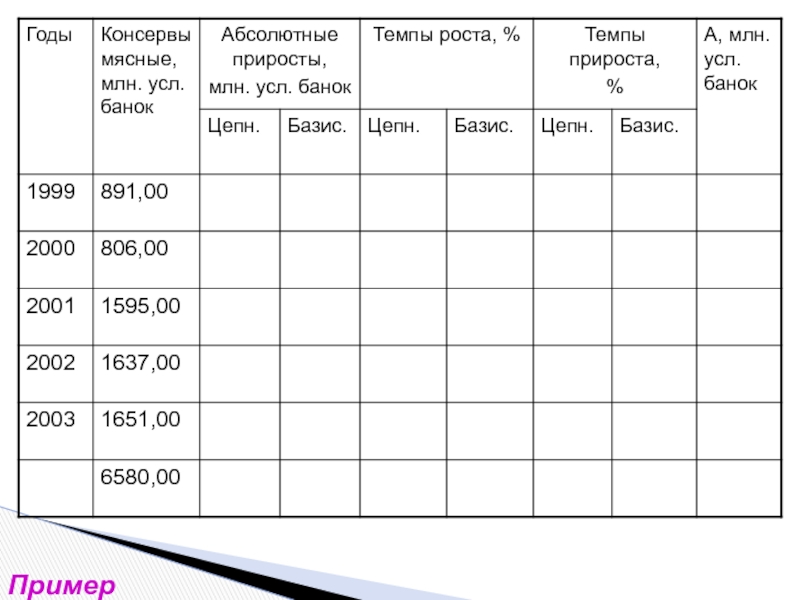
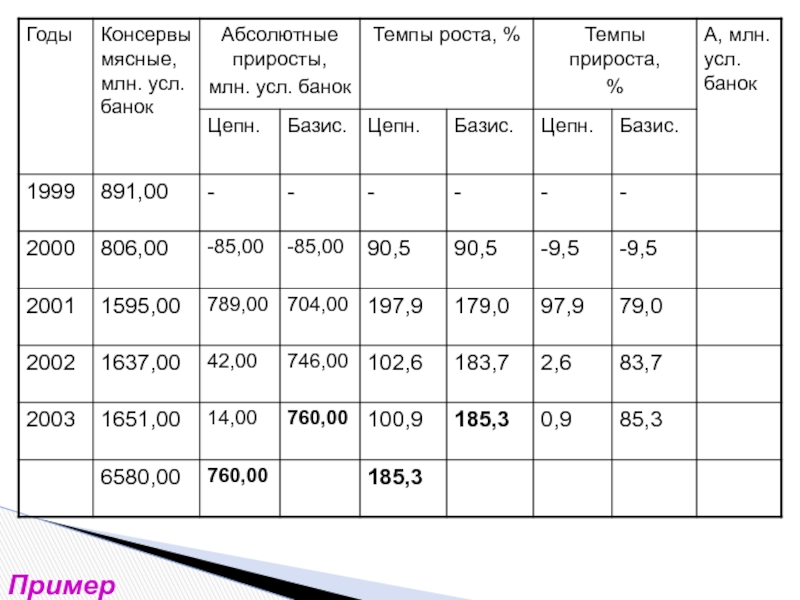
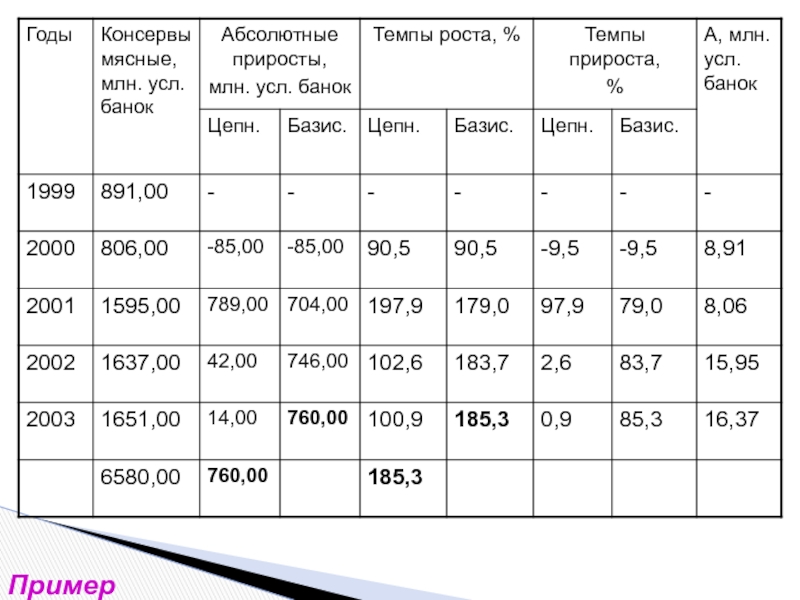
- 13. Пример
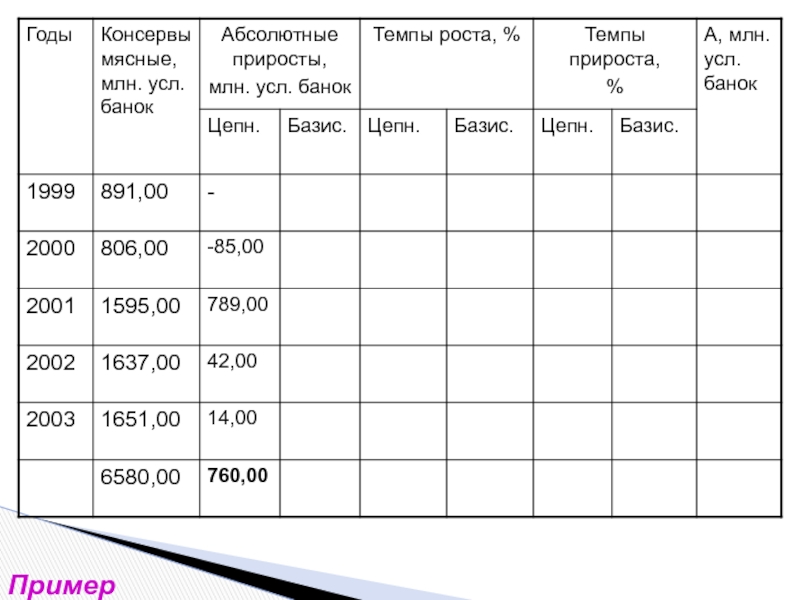
- 14. Пример
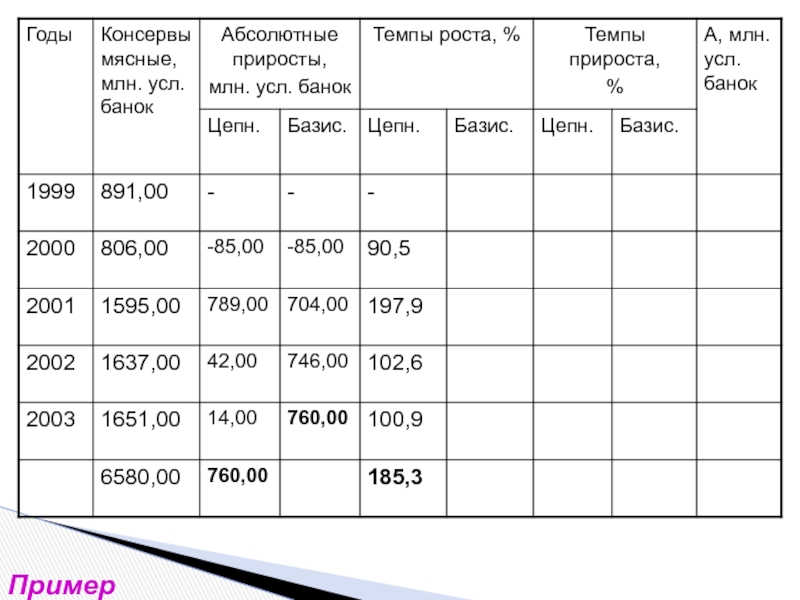
- 15. Пример
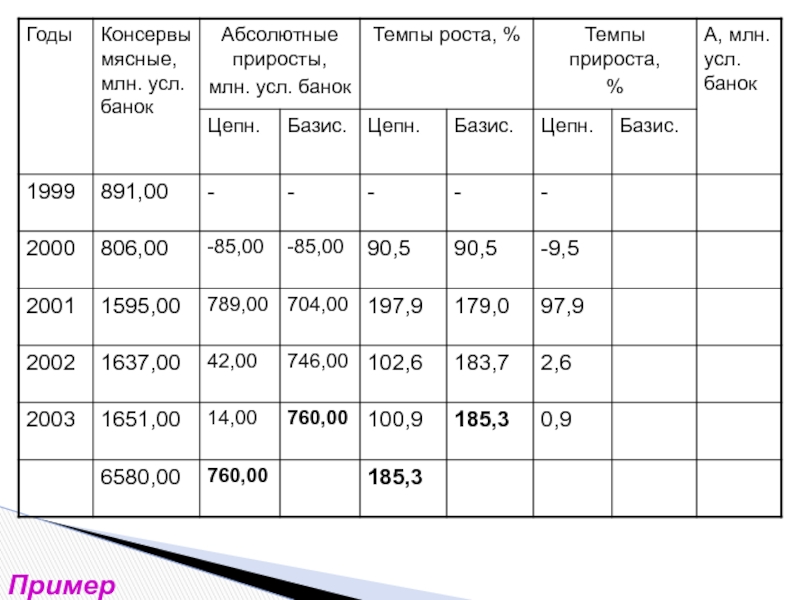
- 16. Пример
- 17. Пример
- 18. Пример
- 19. Пример
- 20. Пример
- 21. Средние Для интервальных рядов с равными периодами
- 22. составляющие: тренд - основная тенденция развития динамического
- 23. этапы: ряд динамики проверяется на наличие тренда;
- 24. методы : Укрупнение интервалов; Скользящая средняя; Аналитическое выравнивание. Непосредственное выделение тренда
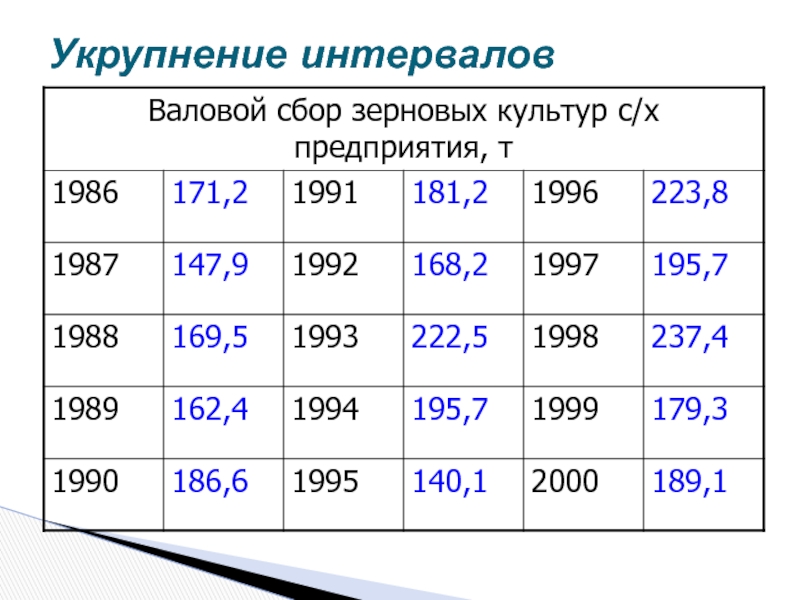
- 25. Укрупнение интервалов
- 26. Укрупнение интервалов
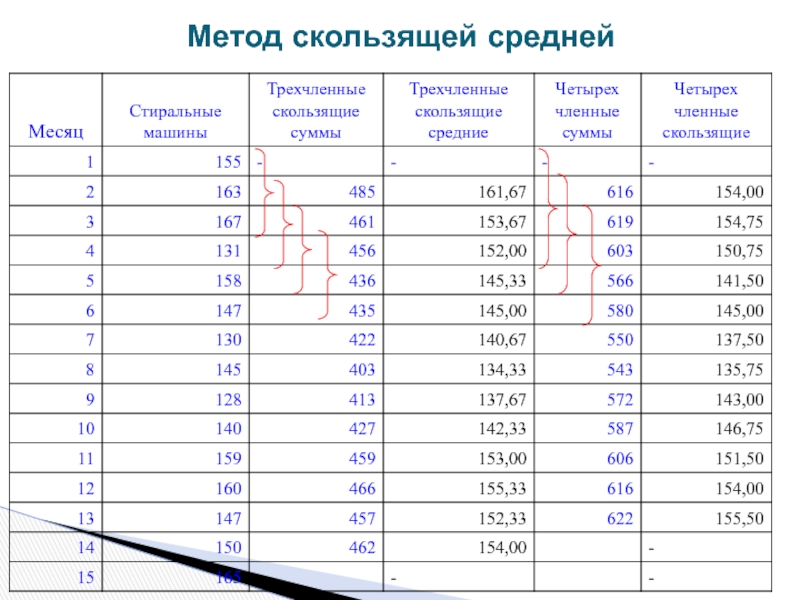
- 27. Метод скользящей средней
- 28. Аналитическое выравнивание где f(t) -
- 29. Аналитическое выравнивание
- 30. Аналитическое выравнивание Линейная зависимость
- 31. Метод наименьших квадратов (МНК) где y
- 32. Метод наименьших квадратов
- 33. Метод наименьших квадратов показатель времени t
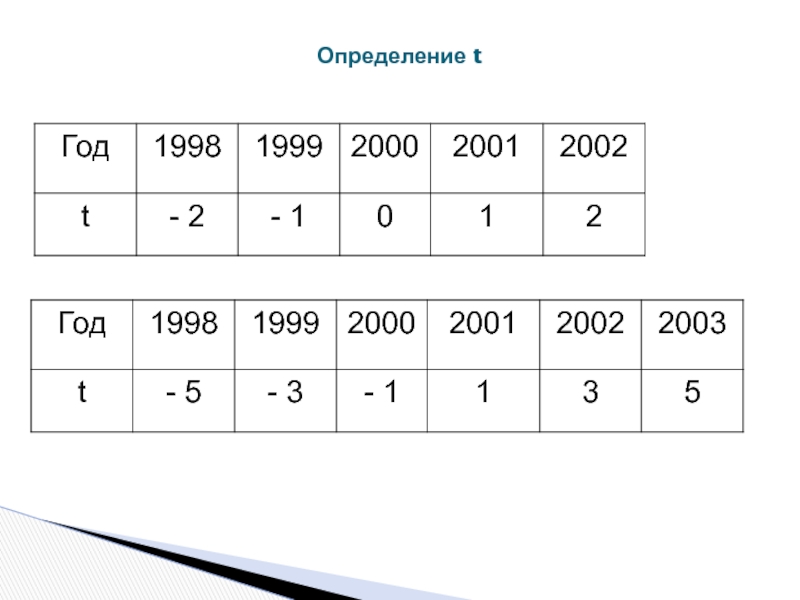
- 34. Определение t
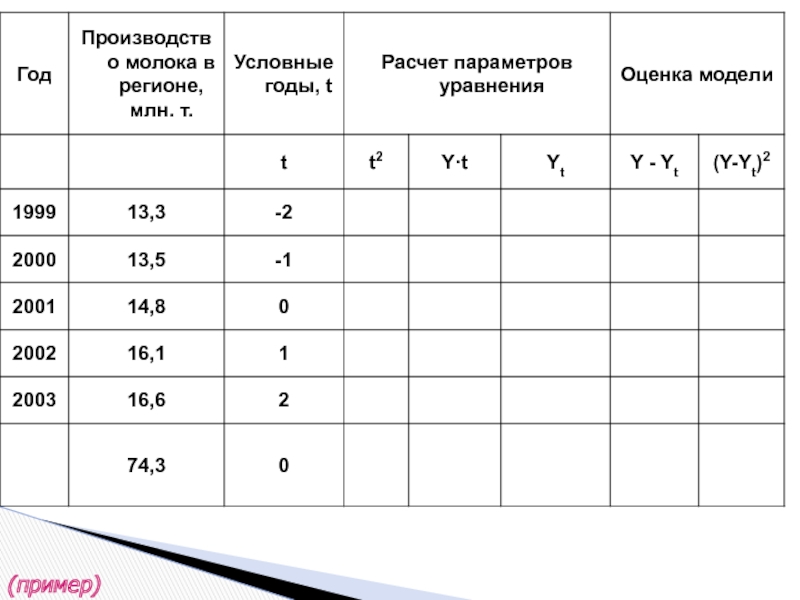
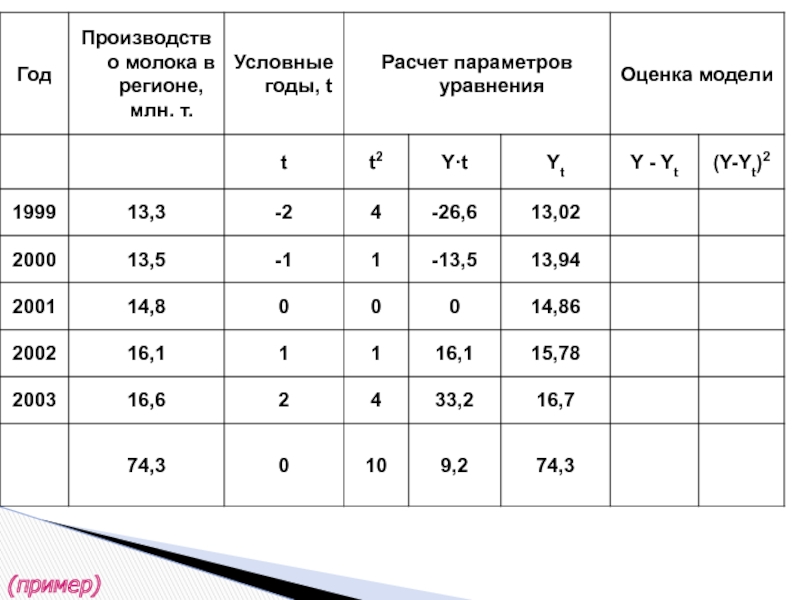
- 35. (пример)
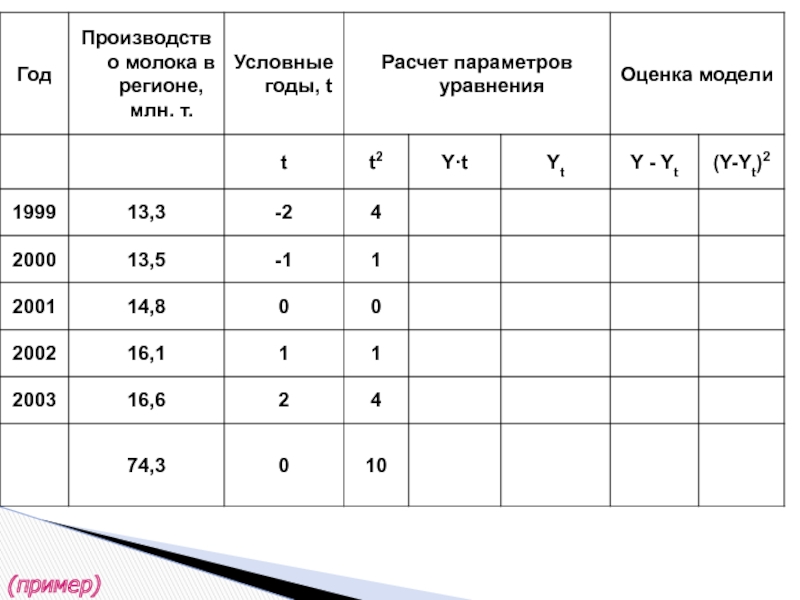
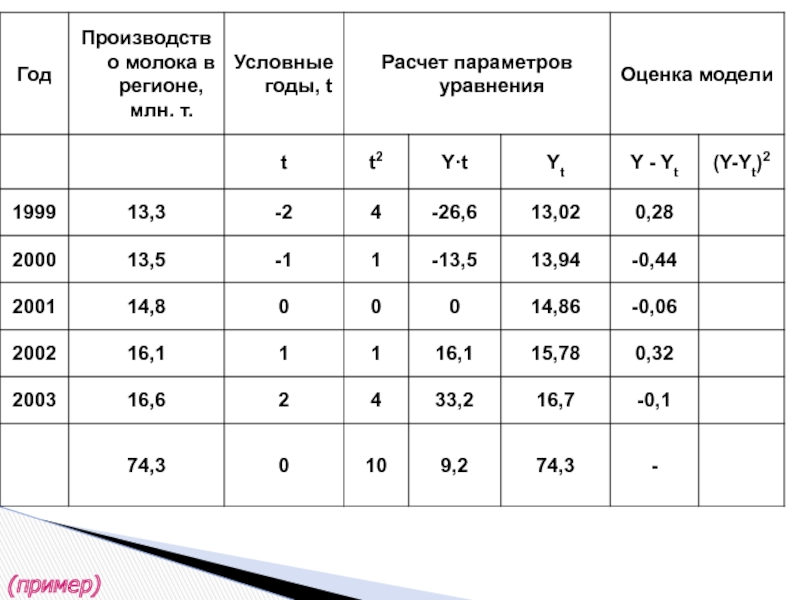
- 36. (пример)
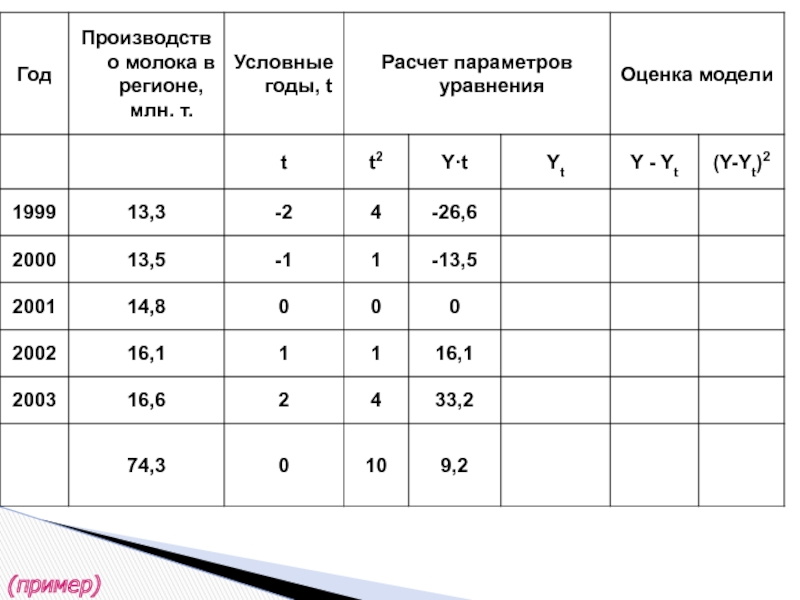
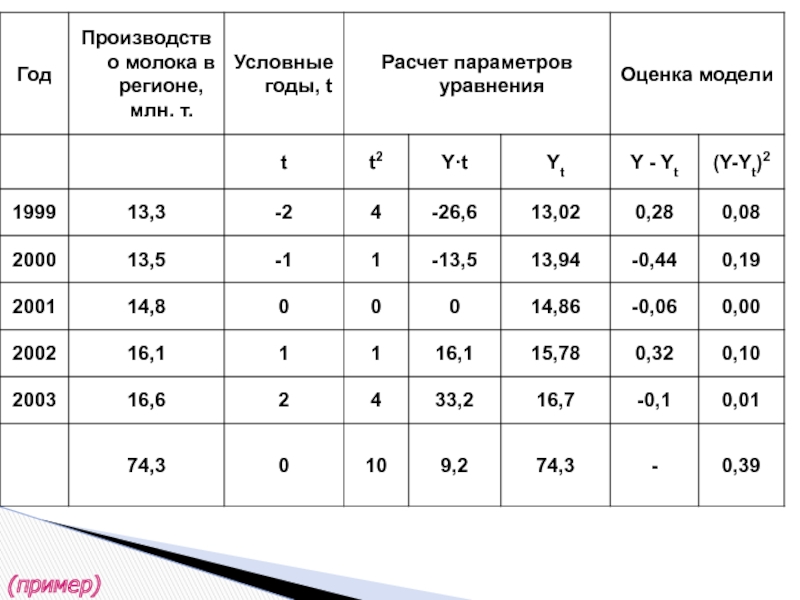
- 37. (пример)
- 38. (пример)
- 39. (пример)
- 40. (пример)
- 41. (пример)
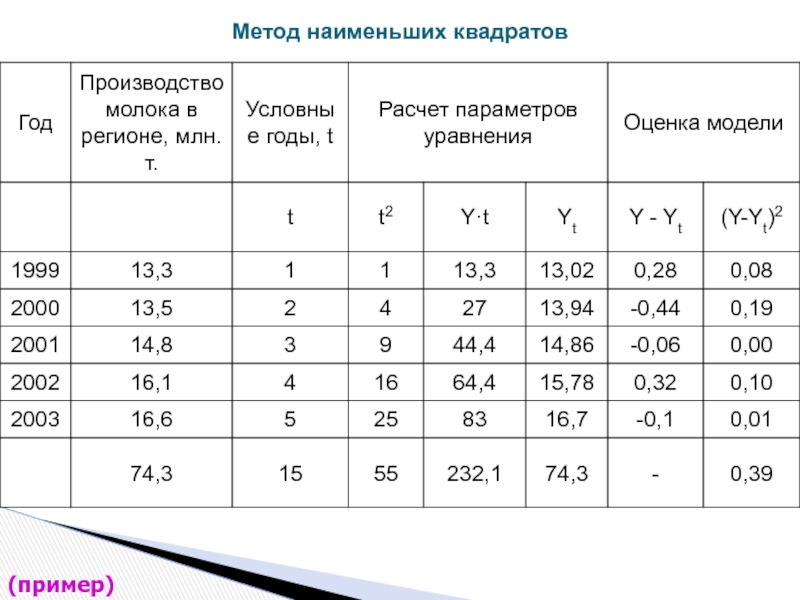
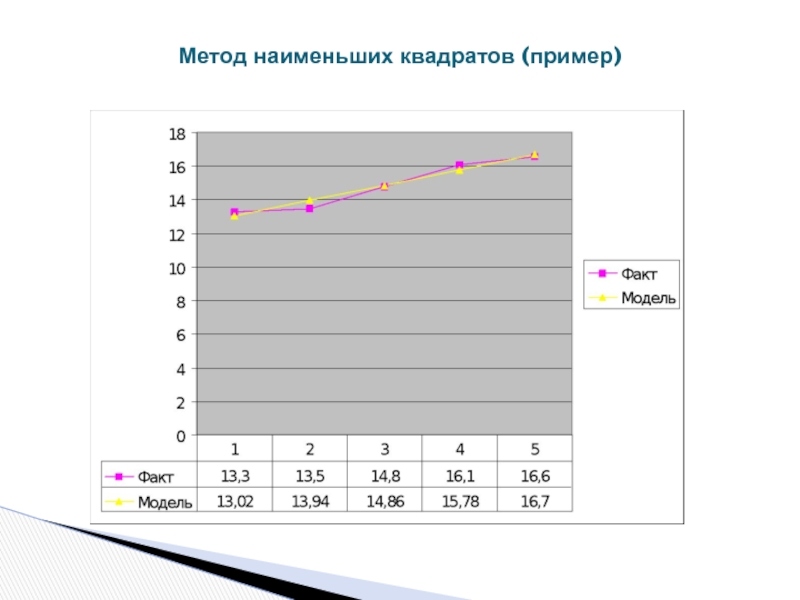
- 44. Метод наименьших квадратов (пример)
- 45. Метод наименьших квадратов (пример)
- 46. Метод наименьших квадратов (пример)
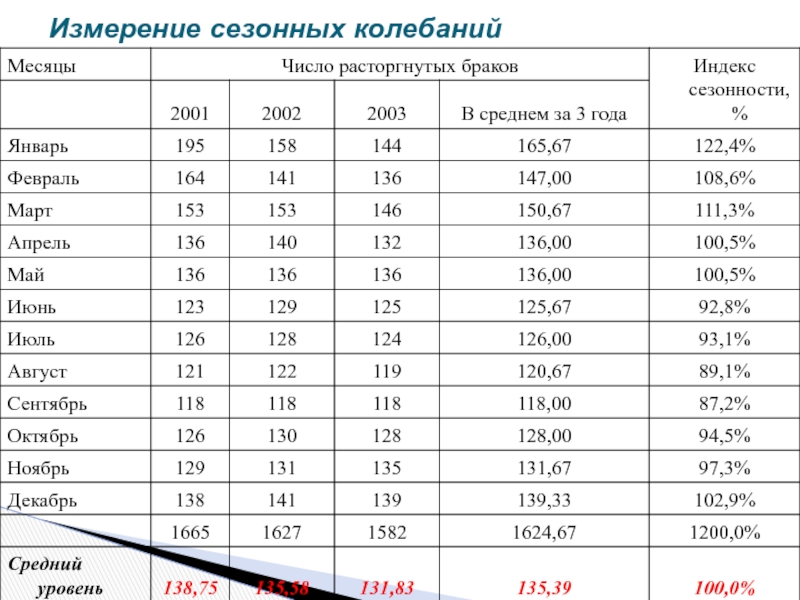
- 47. Измерение сезонных колебаний
- 48. Измерение сезонных колебаний
это последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления. Ряд динамики
Слайд 2 это последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития
изучаемого явления.
Ряд динамики
Слайд 4Примеры рядов динамики
Число дошкольных учреждений в России
(на конец года), тыс.
Моментный
Абсолютных величин
Полный
Абсолютных величин
Полный
Слайд 5Примеры рядов динамики
Моментный
Относительных величин
Полный
Уровень экономической активности населения России
(на начало года), %
Слайд 6Примеры рядов динамики
Интервальный
Средних величин
Неполный
Среднегодовая численность
занятых в экономике
(тыс. чел.)
Слайд 7 Сопоставимость по территории
Сопоставимость по кругу охватываемых объектов
Сопоставимость
по единицам измерения
Упорядоченность во времени
Упорядоченность во времени
Ряд динамики
Слайд 10 средний уровень ряда - показатель, обобщающий итоги развития явления за
единичный интервал или момент из имеющейся временной последовательности
средний абсолютный прирост,
средний темп роста,
средний темп прироста
средний абсолютный прирост,
средний темп роста,
средний темп прироста
Система средних показателей динамики
Слайд 11Средний уровень ряда
Для интервальных рядов с равными периодами времени
Для
интервального ряда с неравноотстоящими уровнями
Для моментного ряда с равноотстоящими уровнями
Для моментного ряда с неравноотстоящими уровнями
Слайд 21Средние
Для интервальных рядов с равными периодами времени
Средний абсолютный прирост
Средний
темп роста
Средний темп прироста
Пример
Слайд 22составляющие:
тренд - основная тенденция развития динамического ряда (к увеличению либо снижению
его уровней);
циклические (периодические) колебания, в том числе сезонные;
случайные колебания.
циклические (периодические) колебания, в том числе сезонные;
случайные колебания.
Изучение тенденции развития
Слайд 23этапы:
ряд динамики проверяется на наличие тренда;
производится выравнивание временного ряда и непосредственное
выделение тренда с экстраполяцией полученных результатов.
Изучение тенденции развития
Слайд 24методы :
Укрупнение интервалов;
Скользящая средняя;
Аналитическое выравнивание.
Непосредственное выделение тренда
Слайд 28Аналитическое выравнивание
где f(t) - уровень, определяемый тенденцией развития;
εt -
случайное и циклическое отклонение от тенденции.
Слайд 30Аналитическое выравнивание
Линейная зависимость - абсолютные цепные приросты, не проявляют тенденции
ни к увеличению, ни к снижению.
Параболическая зависимость - абсолютные цепные приросты обнаруживают некоторую тенденцию развития, но абсолютные цепные приросты абсолютных цепных приростов (разности второго порядка) никакой тенденции развития не проявляют.
Экспоненциальные зависимости - постоянный относительный рост (устойчивость цепных темпов роста, темпов прироста, коэффициентов роста), либо, при отсутствии такого постоянства, - устойчивость в изменении показателей относительного роста (цепных темпов роста цепных же темпов роста, цепных коэффициентов роста цепных же коэффициентов или темпов роста и т. п.).
Параболическая зависимость - абсолютные цепные приросты обнаруживают некоторую тенденцию развития, но абсолютные цепные приросты абсолютных цепных приростов (разности второго порядка) никакой тенденции развития не проявляют.
Экспоненциальные зависимости - постоянный относительный рост (устойчивость цепных темпов роста, темпов прироста, коэффициентов роста), либо, при отсутствии такого постоянства, - устойчивость в изменении показателей относительного роста (цепных темпов роста цепных же темпов роста, цепных коэффициентов роста цепных же коэффициентов или темпов роста и т. п.).
Слайд 31Метод наименьших квадратов (МНК)
где y – исходный уровень ряда динамики,
n –
число членов ряда,
t –показатель времени, который обозначается порядковыми номерами, начиная от низшего.
t –показатель времени, который обозначается порядковыми номерами, начиная от низшего.
Слайд 43
Для определения колеблемости рассчитывается показатель среднего квадратического отклонения:
Относительной мерой колеблемости является
коэффициент вариации:
